- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Решение планиметрических задач на нахождение площадей фигур (9 класс)
Содержание
- 1. Презентация по математике на тему Решение планиметрических задач на нахождение площадей фигур (9 класс)
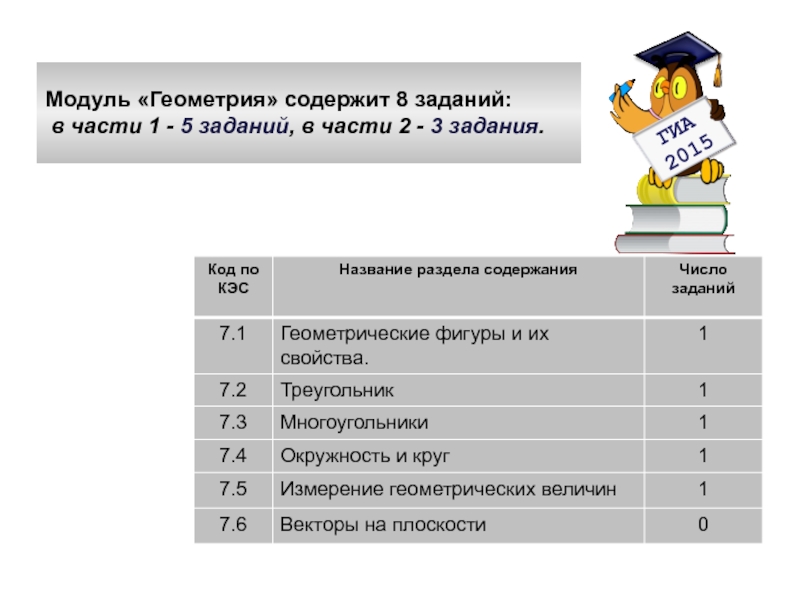
- 2. Модуль «Геометрия» содержит 8 заданий: в части
- 3. Модуль «Геометрия» содержит 8 заданий: в части
- 4. Вашему вниманию представлены тридцать трипрототипа задачи № 12 ГИА – 2015.Прямоугольник.Параллелограмм.Трапеция.Треугольник.Ромб.Круг. Круговой сектор.Формула Пика
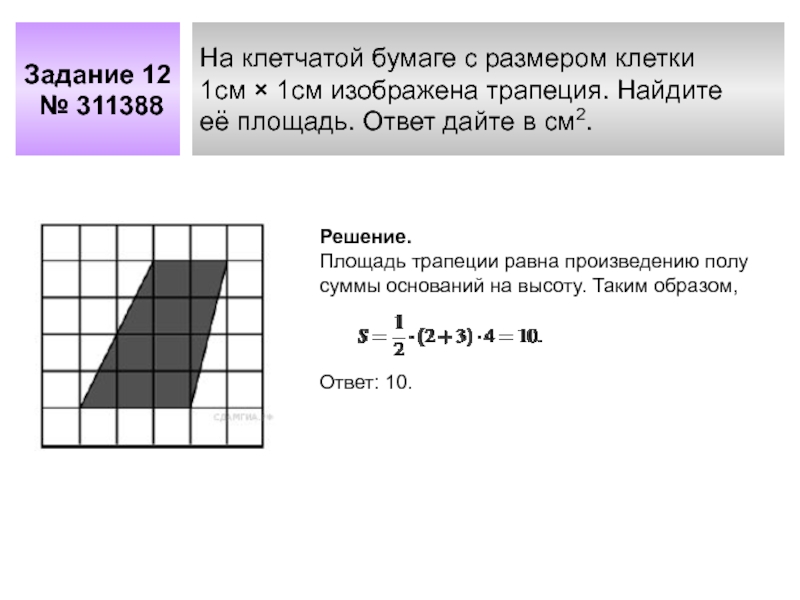
- 5. Задание 12 № 311388На клетчатой бумаге с размером клетки1см
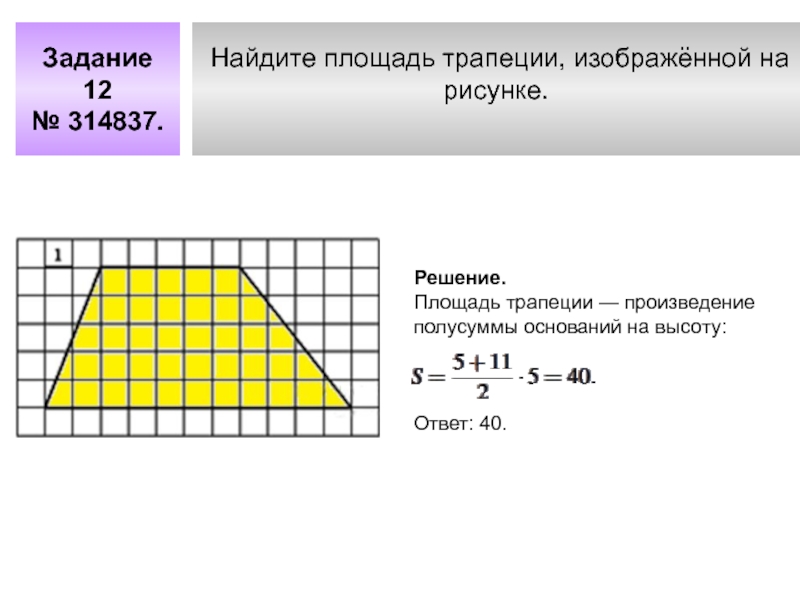
- 6. Задание 12 № 314837.Найдите площадь трапеции, изображённой на рисунке.Решение.Площадь трапеции — произведение полусуммы оснований на высоту: Ответ: 40.
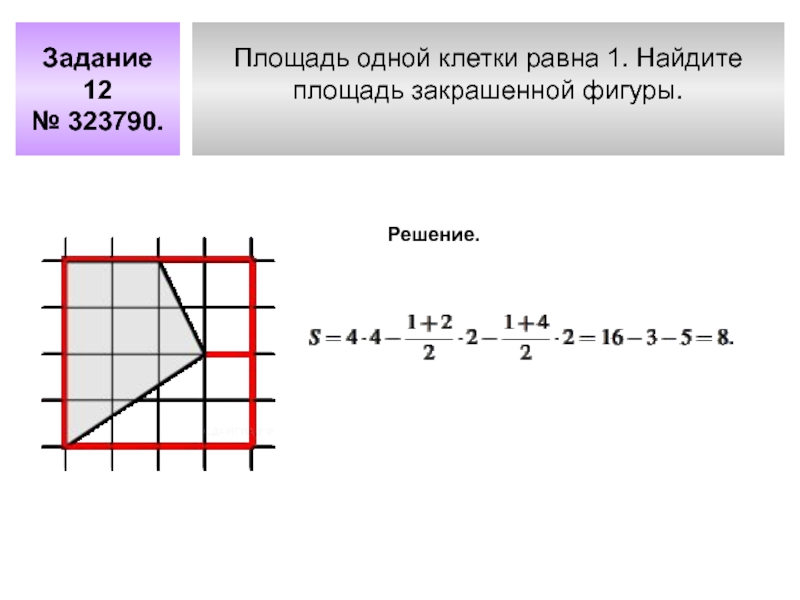
- 7. Задание 12 № 323790.Площадь одной клетки равна 1. Найдите площадь закрашенной фигуры.Решение.
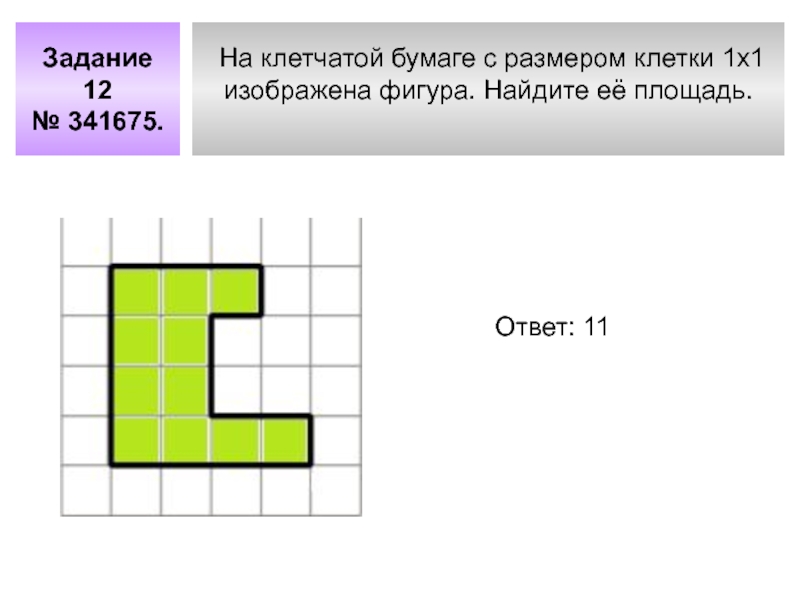
- 8. Задание 12 № 341675.На клетчатой бумаге с размером клетки 1x1 изображена фигура. Найдите её площадь. Ответ: 11
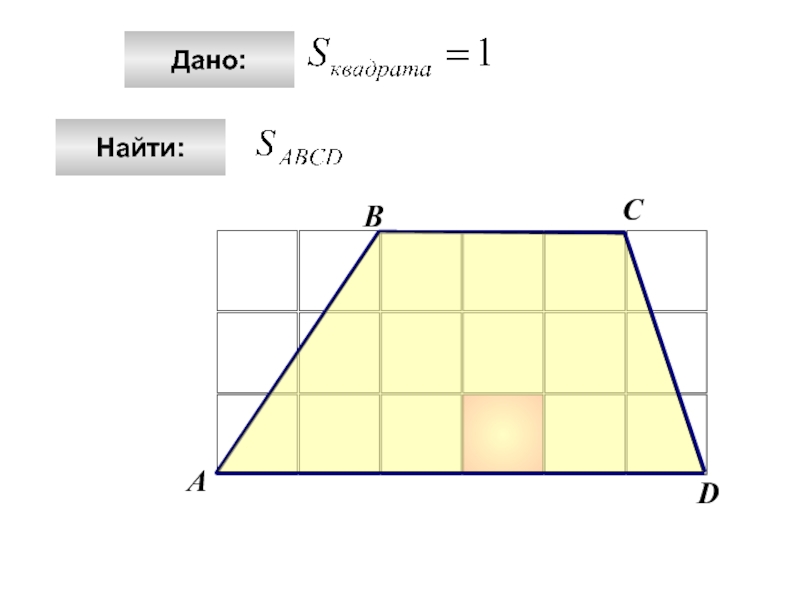
- 9. АBCDДано:Найти:
- 10. Формула Пика позволит вам с необычайной легкостью
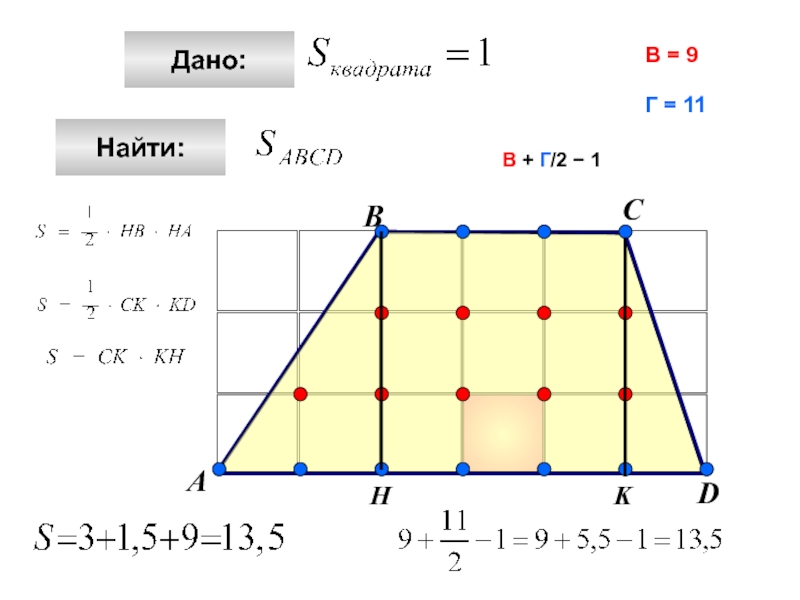
- 11. АBCDДано:Найти:НKВ = 9Г = 11В + Г/2 − 1
- 12. Посмотрим, как применить формулу для вычисления
- 13. В + Г/2 − 1В — есть
- 14. Площадь многоугольника с целочисленными вершинами равна В
- 15. В прямоугольном треугольнике один из катетовравен 10,
- 16. В прямоугольном треугольнике один из катетов равен
- 17. В прямоугольном треугольнике гипотенузаравна 10, а один
- 18. В прямоугольном треугольнике один из катетовравен 10,
- 19. В прямоугольном треугольнике гипотенуза равна 10, а
- 20. В прямоугольном треугольнике один из катетов равен
- 21. В прямоугольном треугольнике один из катетов равен
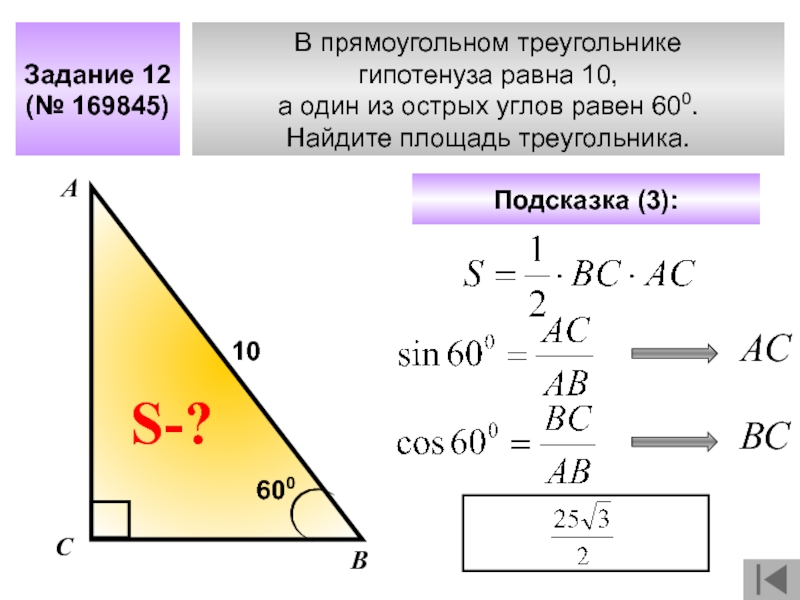
- 22. В прямоугольном треугольнике гипотенуза равна 10, а
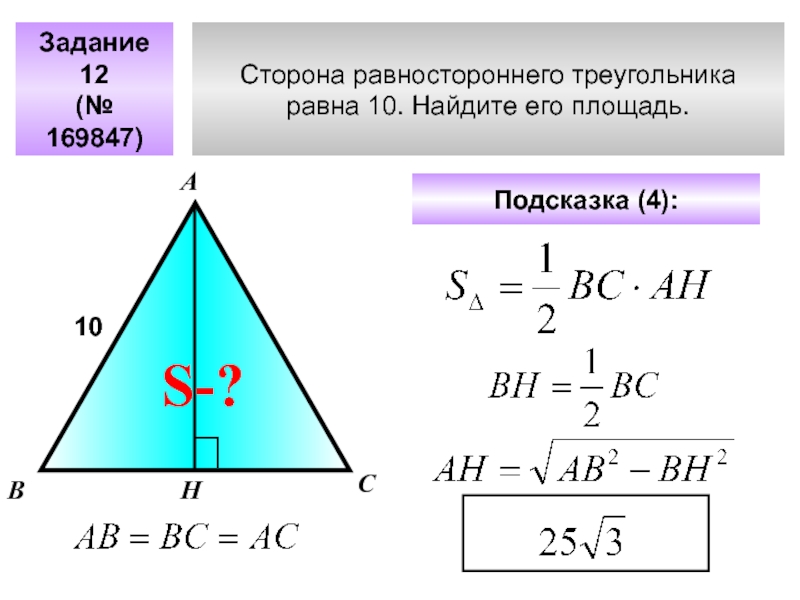
- 23. Сторона равностороннего треугольника равна 10. Найдите его площадь. Задание 12(№ 169847)АВС10Подсказка (4): S-?Н
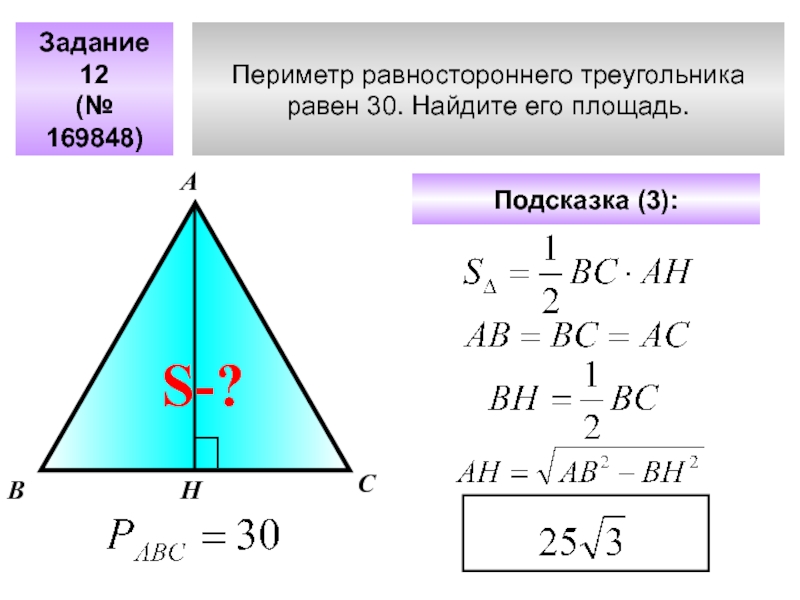
- 24. Периметр равностороннего треугольника равен 30. Найдите его площадь. Задание 12(№ 169848)АВСПодсказка (3): S-?Н
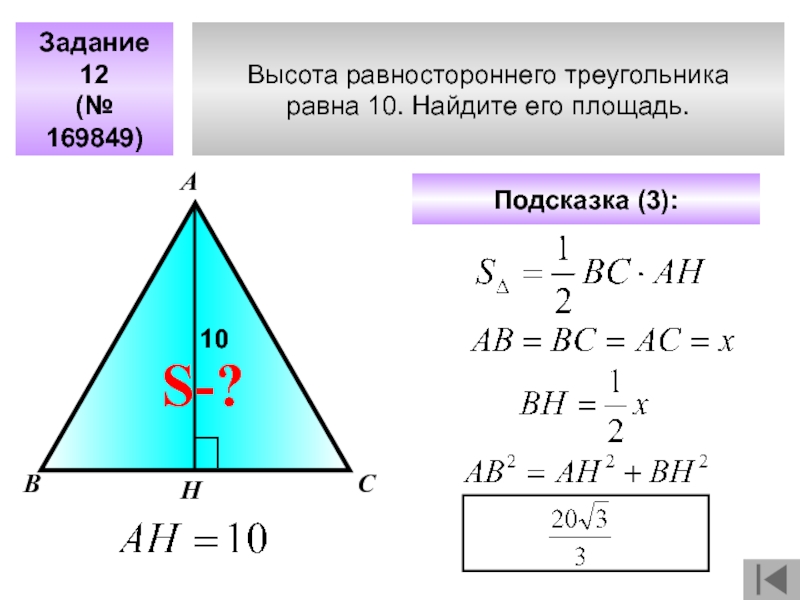
- 25. Высота равностороннего треугольника равна 10. Найдите его площадь. Задание 12(№ 169849)АВСПодсказка (3): S-?Н10
- 26. В равнобедренном треугольнике боковаясторона равна 10, а
- 27. Периметр равнобедренного треугольника равен 16, а боковая
- 28. Периметр равнобедренного треугольника равен 16, а основание — 6. Найдите площадь треугольника. Задание 12(№ 169852)АВСПодсказка (4): S-?НАВ
- 29. В равнобедренном треугольнике боковая сторона равна 10,
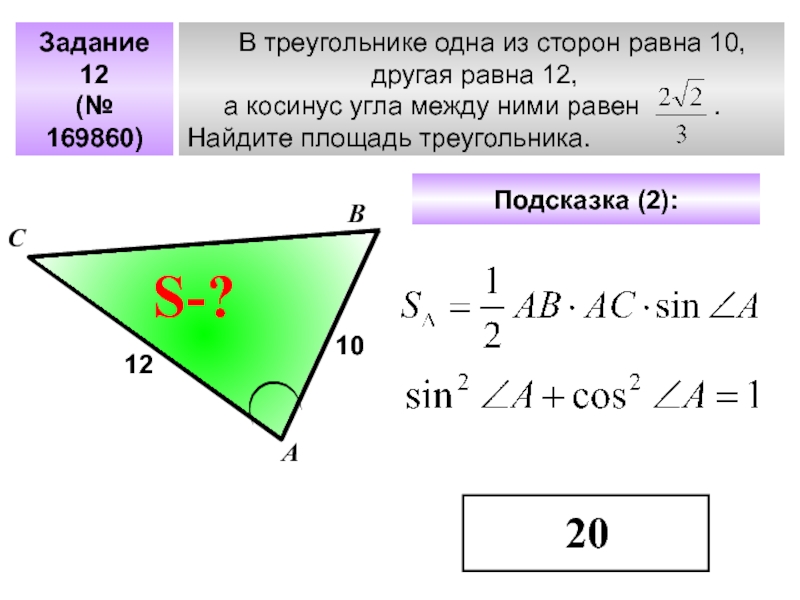
- 30. В треугольнике одна из сторон равна 10,другая
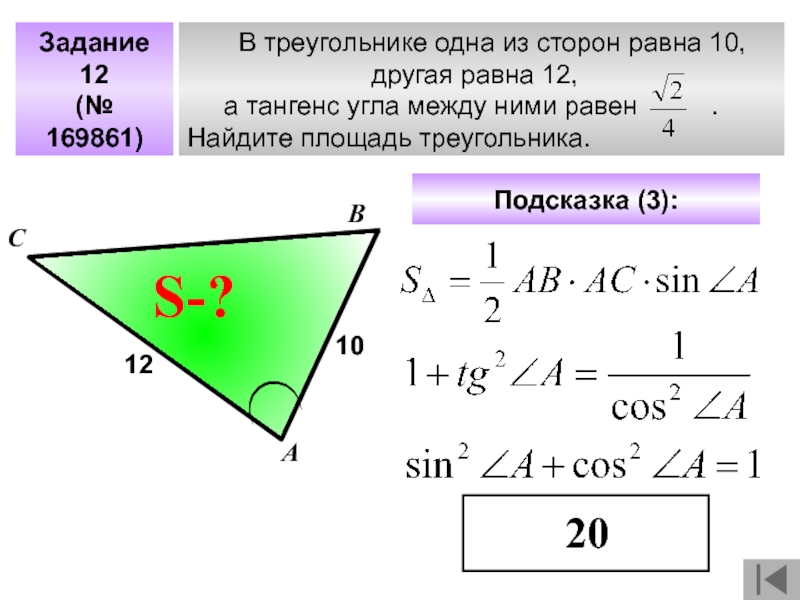
- 31. В треугольнике одна
- 32. В треугольнике одна
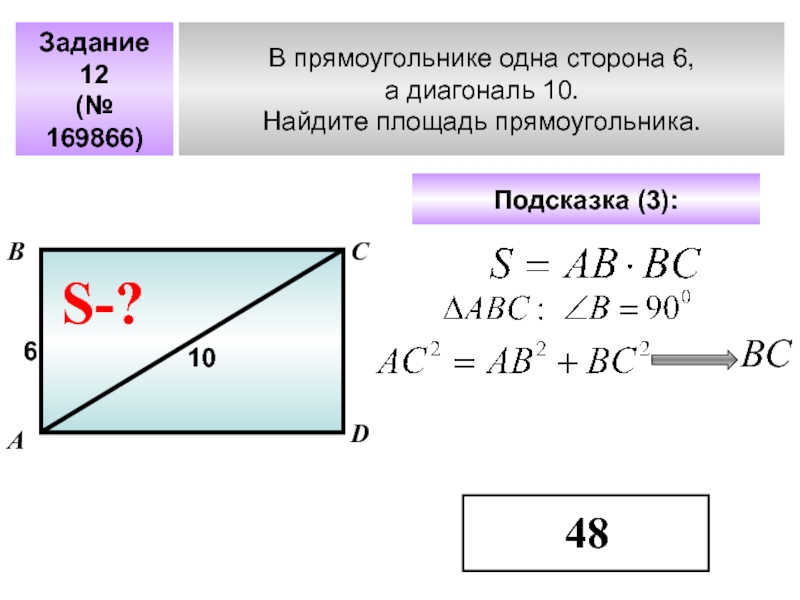
- 33. В прямоугольнике одна сторона 6,а диагональ 10. Найдите площадь прямоугольника. АВСЗадание 12(№ 169866)6Подсказка (3): S-?10DВC48
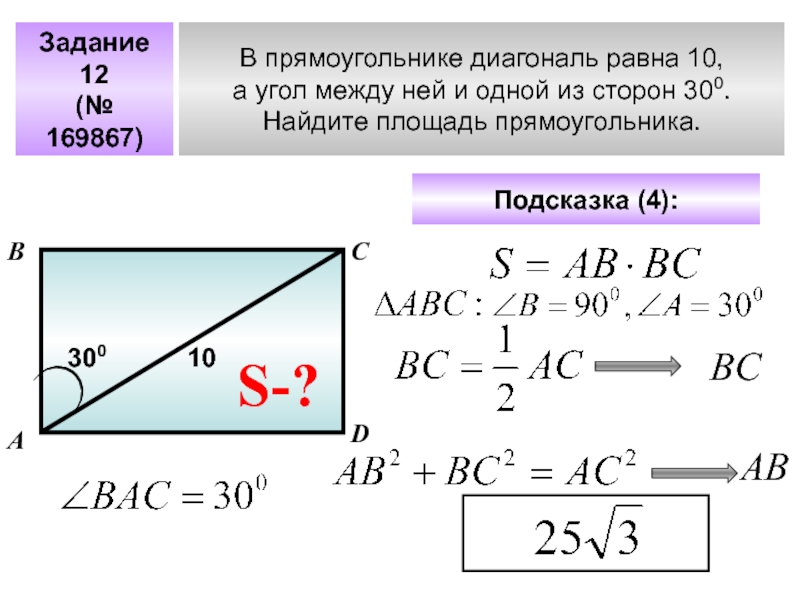
- 34. В прямоугольнике диагональ равна 10,а угол между
- 35. В прямоугольнике диагональ равна 10, угол между
- 36. Задание 12(№ 169868)Сторона ромба равна 5, а диагональ равна 6. Найдите площадь ромба. АВСDПодсказка (4): 5S-?6НАН24
- 37. Задание 12(№ 169868)Периметр ромба равен 40, а
- 38. Задание 12(№ 169874)Периметр ромба равен 24, а
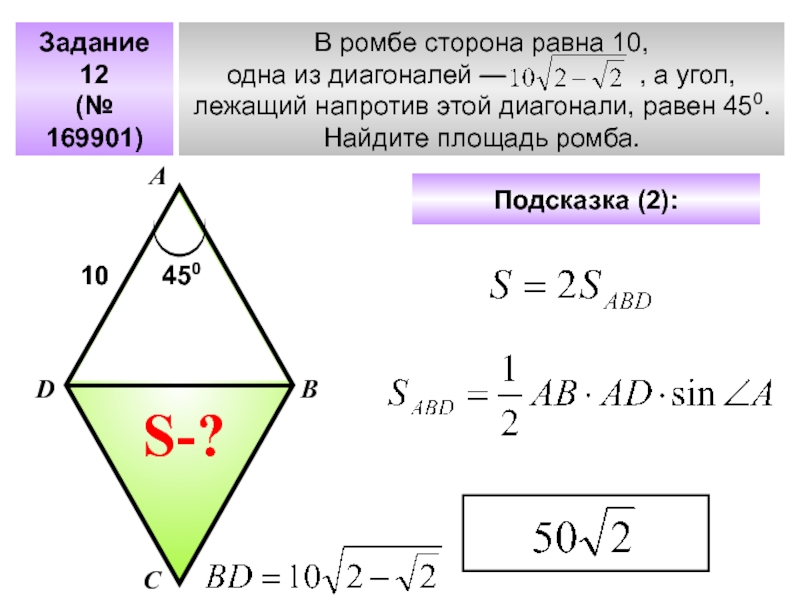
- 39. Задание 12(№ 169901)В ромбе сторона равна 10,
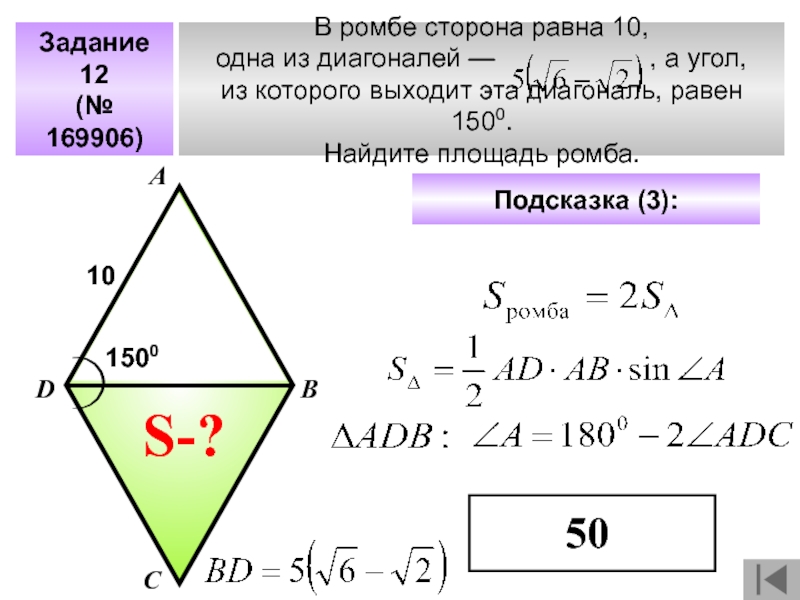
- 40. Задание 12(№ 169906)В ромбе сторона равна 10,
- 41. Задание 12(№ 169876)Одна из сторон параллелограмма равна
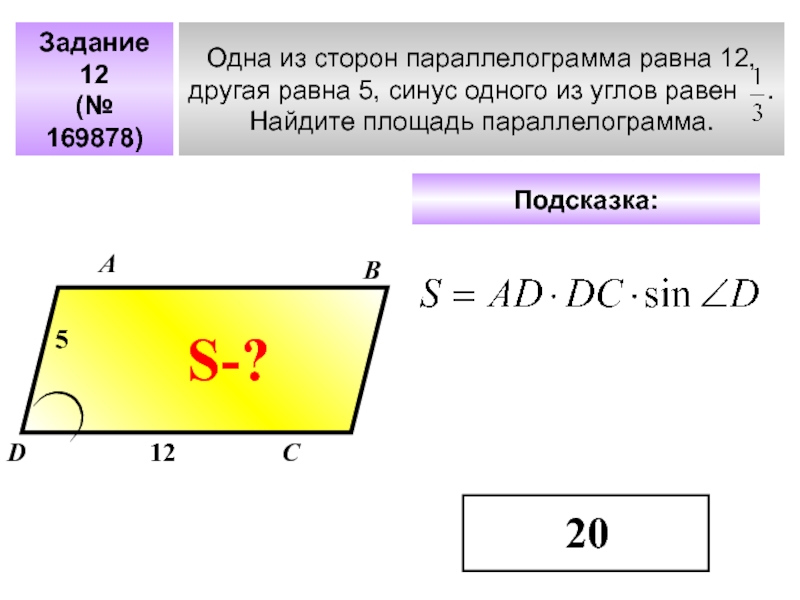
- 42. Задание 12(№ 169878)Одна из сторон параллелограмма равна
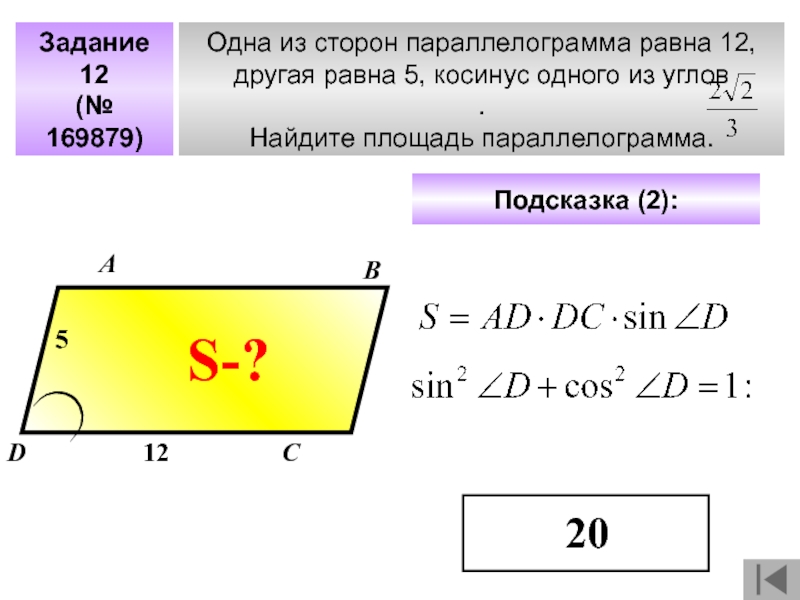
- 43. Задание 12(№ 169879)Одна из сторон параллелограмма равна
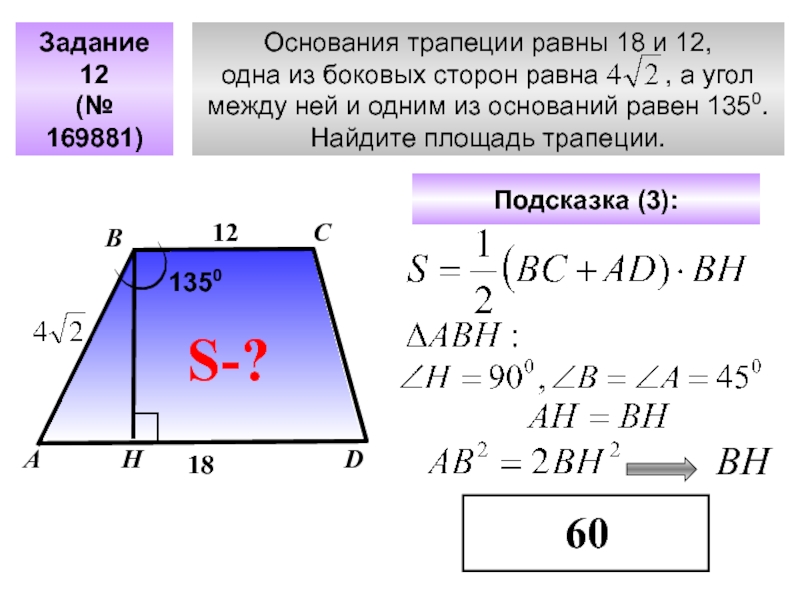
- 44. Основания трапеции равны 18 и 12, одна
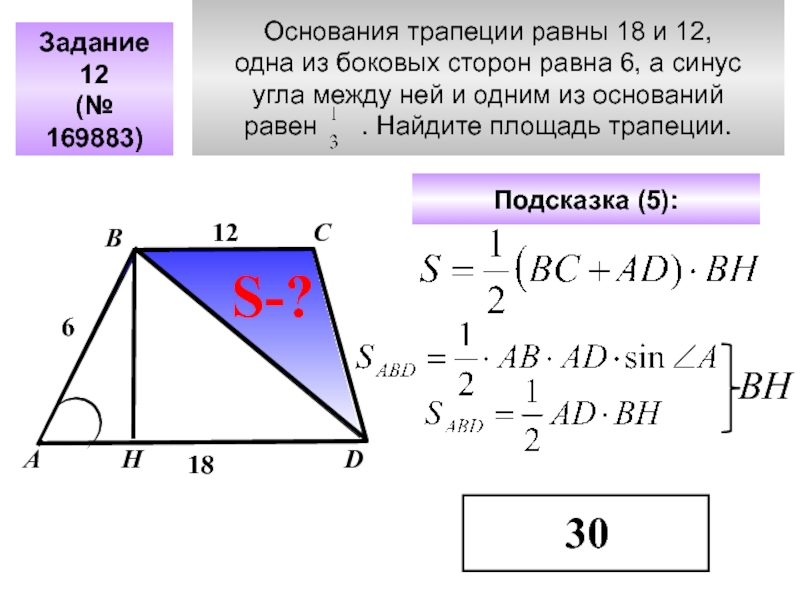
- 45. Основания трапеции равны 18 и 12, одна
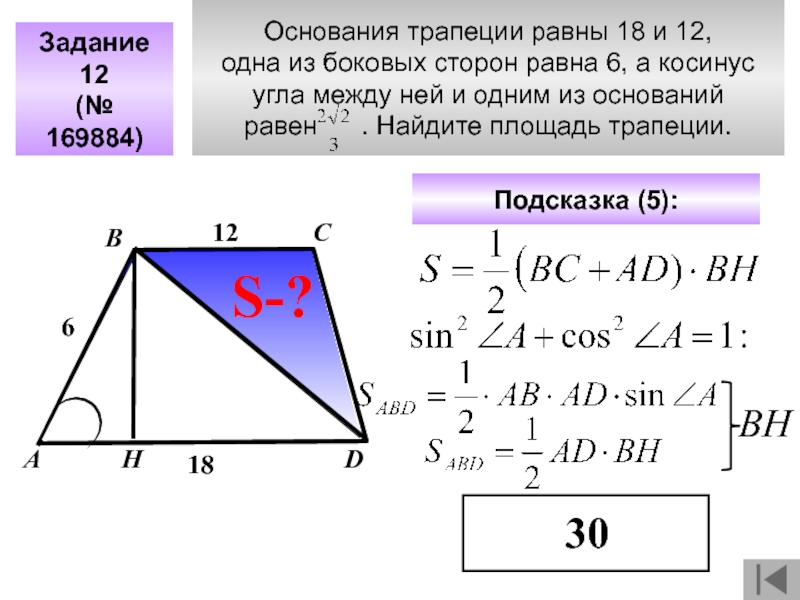
- 46. Основания трапеции равны 18 и 12, одна
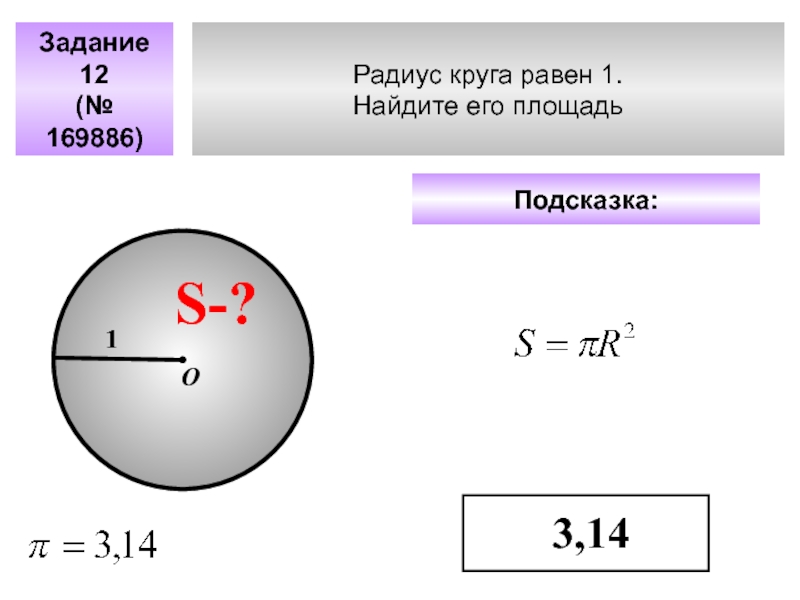
- 47. Радиус круга равен 1. Найдите его площадь Задание 12(№ 169886)Подсказка: 3,14S-?1О
- 48. Найдите площадь кругового сектора, если радиус круга
- 49. Найдите площадь кругового сектора, если длина ограничивающей
- 50. Радиус круга равен 3, а длина ограничивающей
- 51. http://www.mathgia.ruПри создании презентации были использованызадачи с сайта«Открытый банк заданий по математике»ГИА – 2015.
Слайд 3Модуль «Геометрия» содержит 8 заданий: в части 1 - 5 заданий,
ти 2 - 3 задания.
Перечень элементов содержания,
проверяемых на ГИА
Слайд 4Вашему вниманию представлены
тридцать три
прототипа задачи № 12
ГИА – 2015.
Прямоугольник.
Параллелограмм.
Трапеция.
Треугольник.
Ромб.
Круг.
Формула Пика
Слайд 5Задание 12
№ 311388
На клетчатой бумаге с размером клетки
1см × 1см изображена трапеция.
её площадь. Ответ дайте в см2.
Решение.
Площадь трапеции равна произведению полусуммы оснований на высоту. Таким образом,
Ответ: 10.
Слайд 6Задание 12
№ 314837.
Найдите площадь трапеции, изображённой на
рисунке.
Решение.
Площадь трапеции — произведение полусуммы
Ответ: 40.
Слайд 7Задание 12
№ 323790.
Площадь одной клетки равна 1. Найдите
площадь закрашенной фигуры.
Решение.
Слайд 8Задание 12
№ 341675.
На клетчатой бумаге с размером клетки 1x1
изображена фигура. Найдите
Ответ: 11
Слайд 10Формула Пика позволит вам с необычайной легкостью находить площадь любого многоугольника
Именно такие задания предлагают на ЕГЭ в задании В3.
Площадь многоугольника с целочисленными вершинами равна
где В — количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.
Формула Пика очень удобна когда сложно догадаться, как разбить фигуру на удобные многоугольники или достроить…
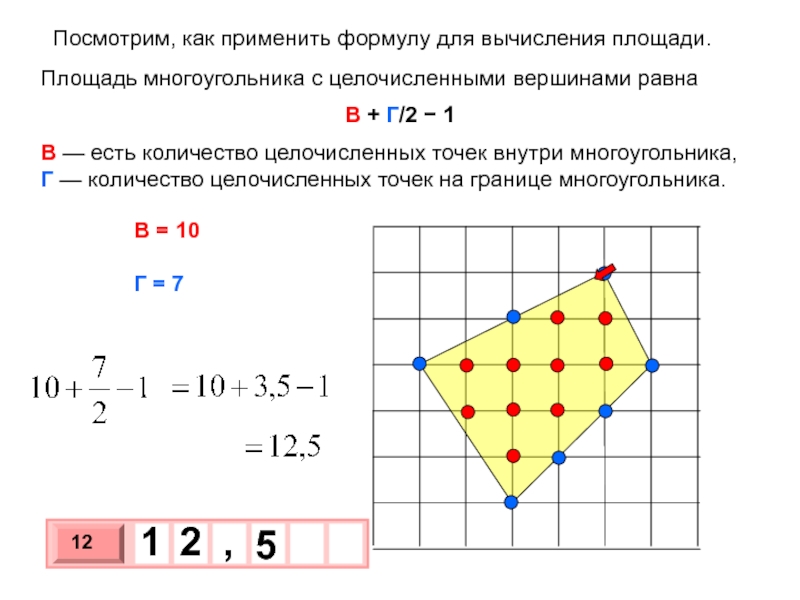
Слайд 12 Посмотрим, как применить формулу для вычисления площади.
Площадь многоугольника с целочисленными
В + Г/2 − 1
В — есть количество целочисленных точек внутри многоугольника, Г — количество целочисленных точек на границе многоугольника.
В = 10
Г = 7
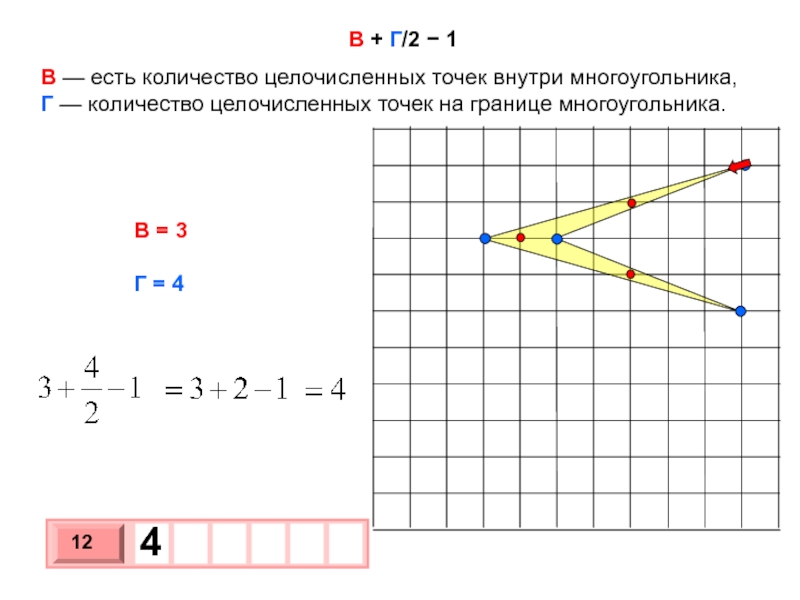
Слайд 13 В + Г/2 − 1
В — есть количество целочисленных точек внутри
В = 3
Г = 4
Слайд 14Площадь многоугольника с целочисленными вершинами равна
В + Г/2 − 1
В —
В = 0
Г = 4
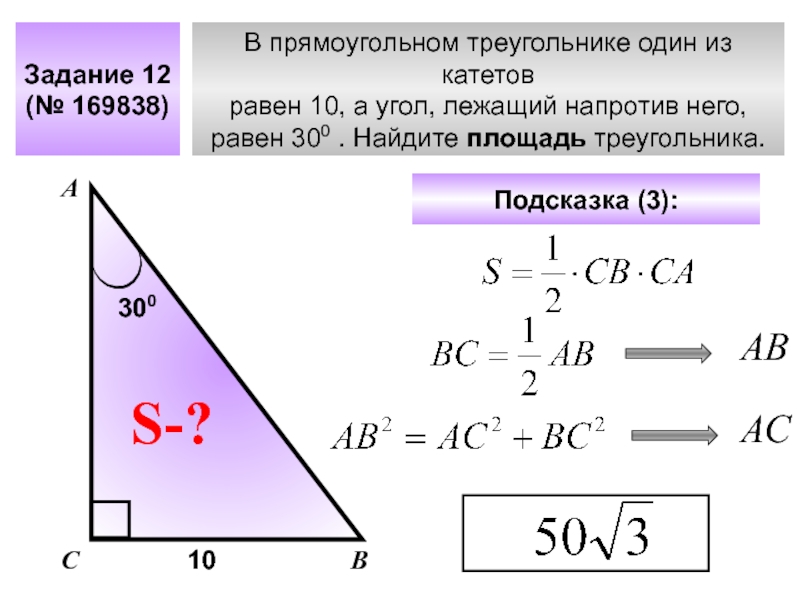
Слайд 15В прямоугольном треугольнике один из катетов
равен 10, а угол, лежащий напротив
равен 300 . Найдите площадь треугольника.
Задание 12
(№ 169838)
А
В
С
S-?
Подсказка (3):
10
300
АВ
АС
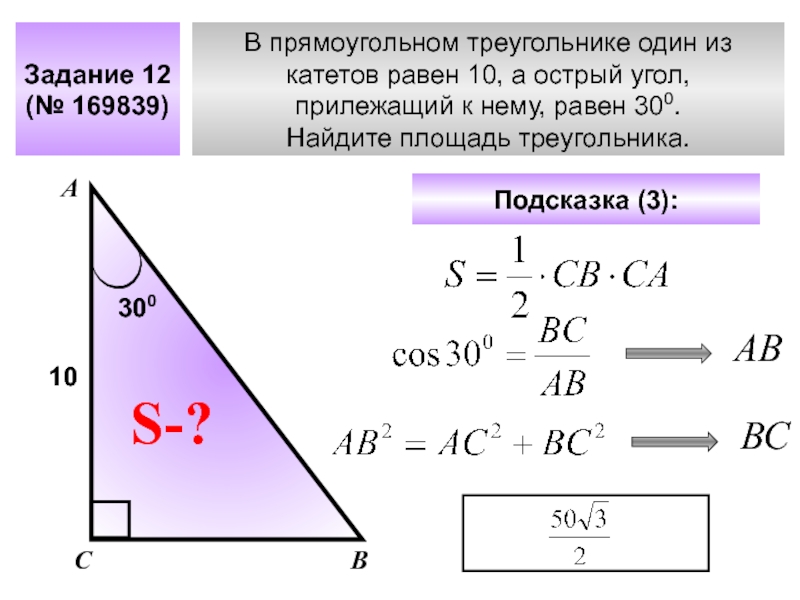
Слайд 16В прямоугольном треугольнике один из
катетов равен 10, а острый угол,
прилежащий к нему, равен 300.
Найдите площадь треугольника.
Задание 12
(№ 169839)
А
В
С
S-?
Подсказка (3):
10
300
АВ
ВС
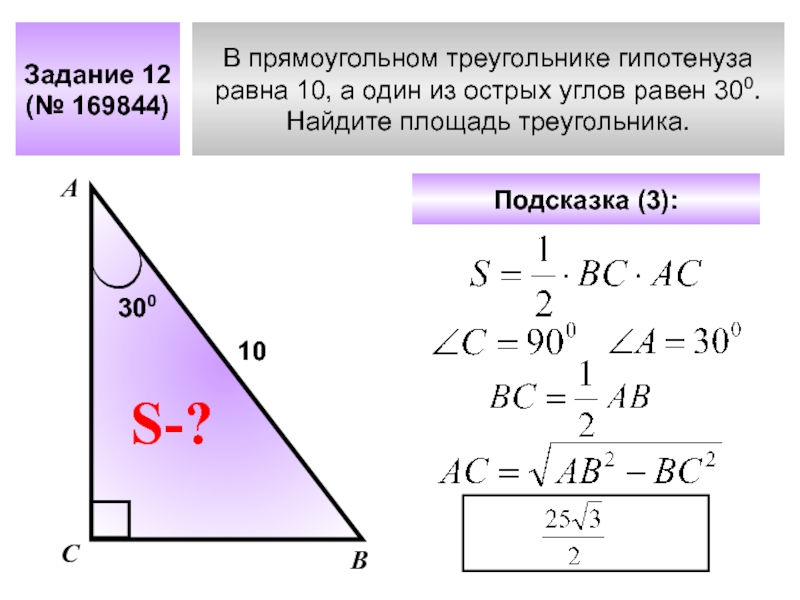
Слайд 17В прямоугольном треугольнике гипотенуза
равна 10, а один из острых углов равен
Найдите площадь треугольника.
Задание 12
(№ 169844)
Подсказка (3):
А
В
С
S-?
10
300
Слайд 18В прямоугольном треугольнике один из катетов
равен 10, а угол, лежащий напротив
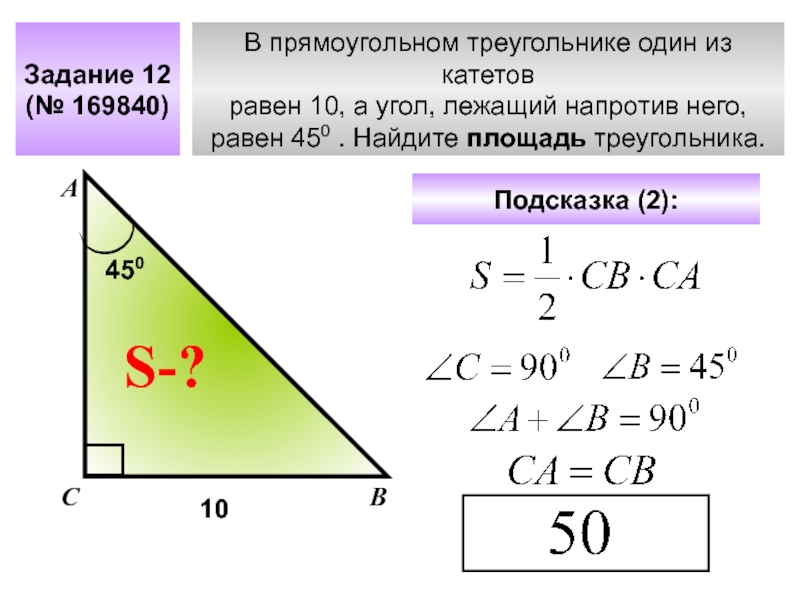
равен 450 . Найдите площадь треугольника.
Задание 12
(№ 169840)
А
В
С
S-?
Подсказка (2):
10
450
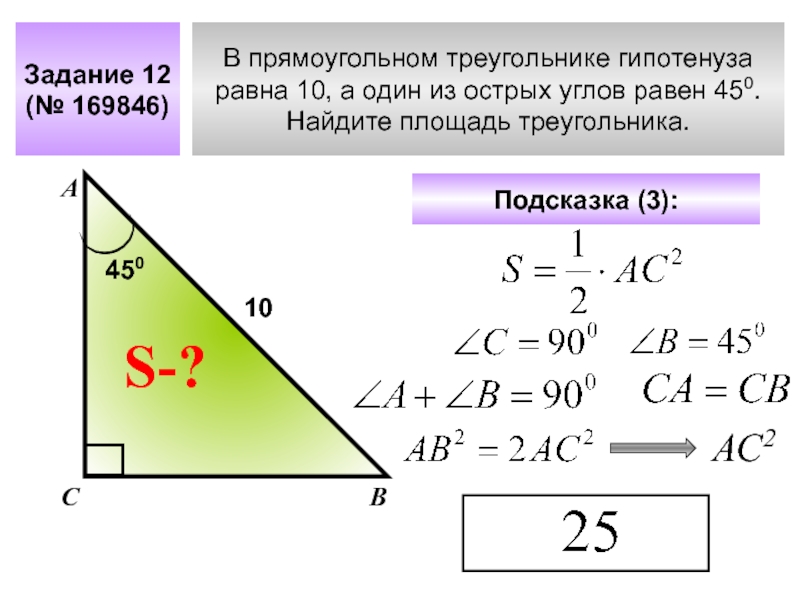
Слайд 19В прямоугольном треугольнике гипотенуза
равна 10, а один из острых углов
Найдите площадь треугольника.
Задание 12
(№ 169846)
А
В
С
S-?
Подсказка (3):
10
450
АС2
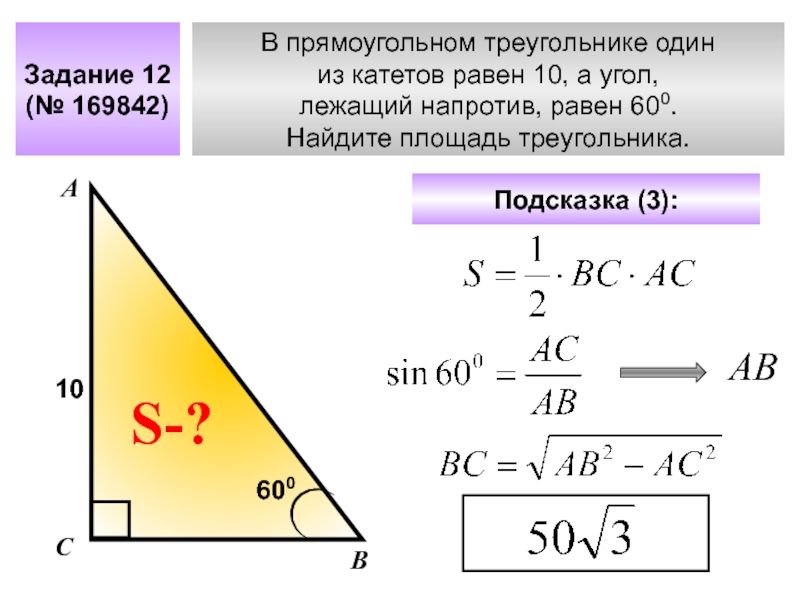
Слайд 20В прямоугольном треугольнике один
из катетов равен 10, а угол,
лежащий
Найдите площадь треугольника.
Задание 12
(№ 169842)
Подсказка (3):
А
В
С
S-?
10
600
АВ
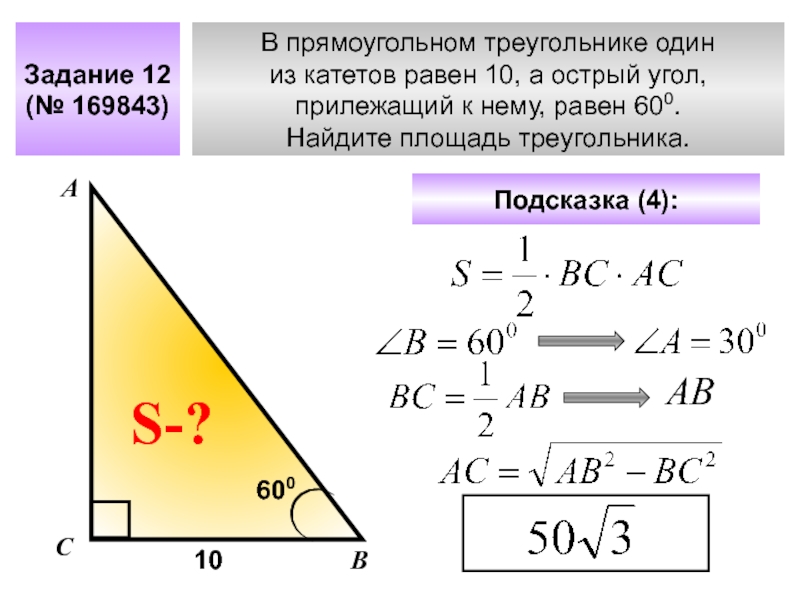
Слайд 21В прямоугольном треугольнике один
из катетов равен 10, а острый угол,
прилежащий к нему, равен 600.
Найдите площадь треугольника.
Задание 12
(№ 169843)
Подсказка (4):
А
В
С
S-?
10
600
АВ
Слайд 22В прямоугольном треугольнике
гипотенуза равна 10,
а один из острых углов
Найдите площадь треугольника.
Задание 12
(№ 169845)
Подсказка (3):
А
В
С
S-?
10
600
АС
ВС
Слайд 23Сторона равностороннего треугольника
равна 10. Найдите его площадь.
Задание 12
(№ 169847)
А
В
С
10
Подсказка
S-?
Н
Слайд 24Периметр равностороннего треугольника
равен 30. Найдите его площадь.
Задание 12
(№ 169848)
А
В
С
Подсказка
S-?
Н
Слайд 25Высота равностороннего треугольника
равна 10. Найдите его площадь.
Задание 12
(№ 169849)
А
В
С
Подсказка
S-?
Н
10
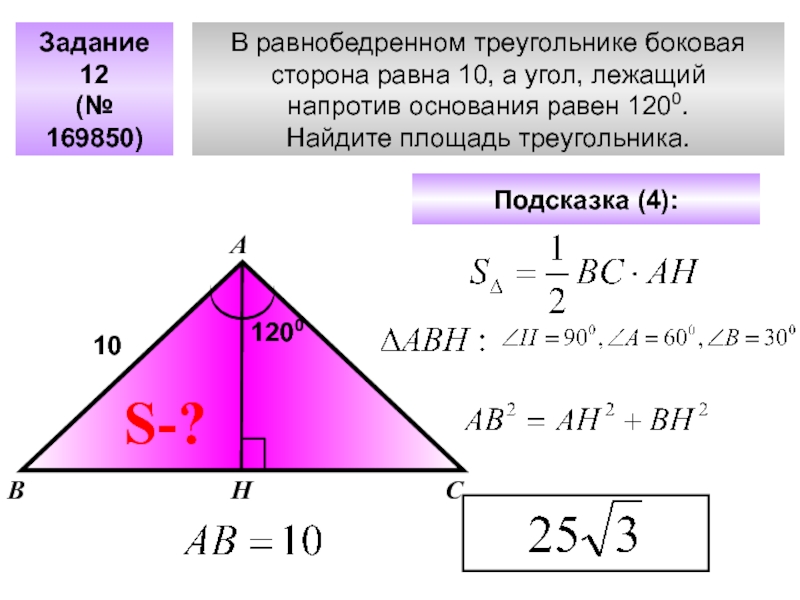
Слайд 26В равнобедренном треугольнике боковая
сторона равна 10, а угол, лежащий
напротив основания
Найдите площадь треугольника.
Задание 12
(№ 169850)
А
В
С
Подсказка (4):
S-?
Н
10
1200
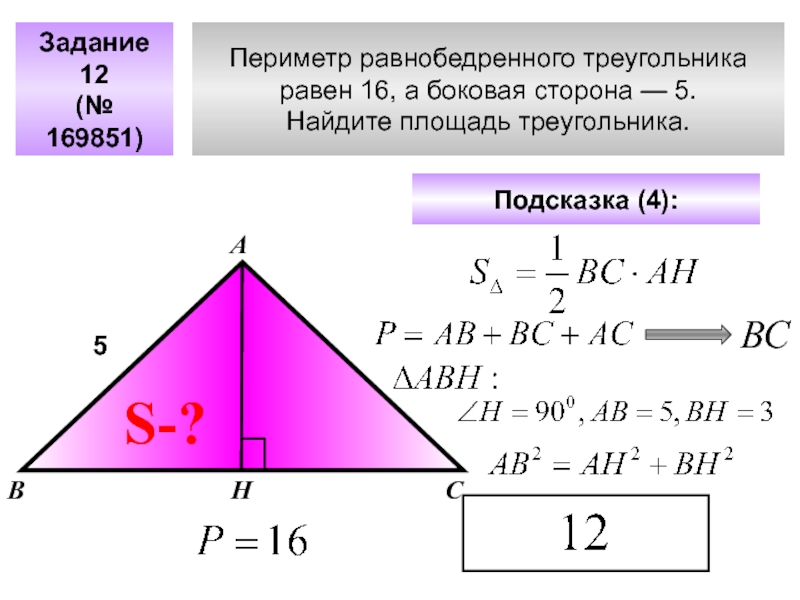
Слайд 27Периметр равнобедренного треугольника
равен 16, а боковая сторона — 5.
Найдите площадь
Задание 12
(№ 169851)
А
В
С
Подсказка (4):
S-?
Н
5
ВС
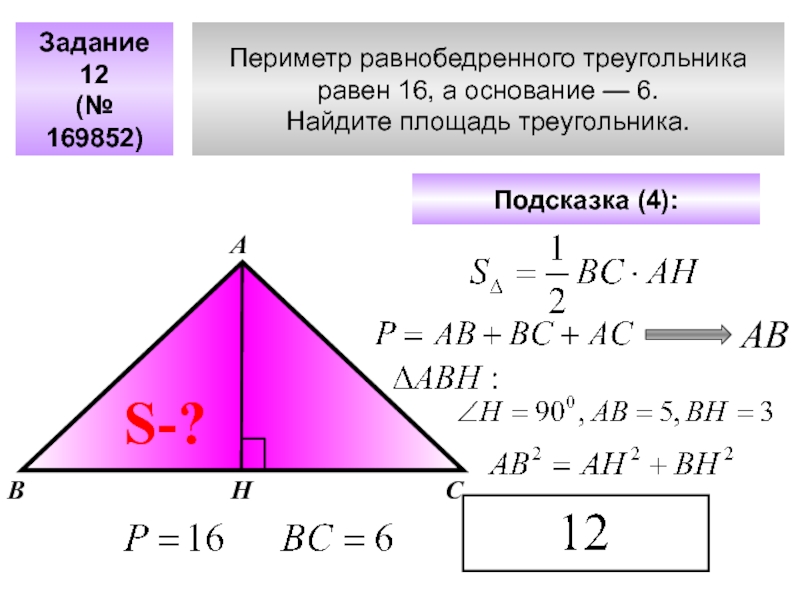
Слайд 28Периметр равнобедренного треугольника
равен 16, а основание — 6.
Найдите площадь треугольника.
Задание 12
(№ 169852)
А
В
С
Подсказка (4):
S-?
Н
АВ
Слайд 29В равнобедренном треугольнике боковая
сторона равна 10, основание —
а угол, лежащий напротив основания,
равен 1350. Найдите площадь треугольника.
Задание 12
(№ 169896)
А
В
С
Подсказка (2):
S-?
1350
10
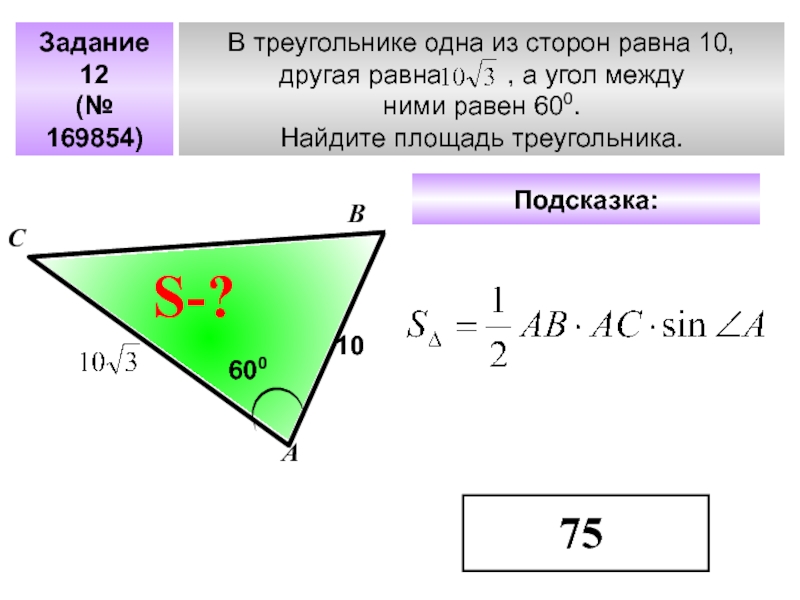
Слайд 30В треугольнике одна из сторон равна 10,
другая равна
ними равен 600.
Найдите площадь треугольника.
А
В
С
?
Задание 12
(№ 169854)
10
600
S-?
Подсказка:
75
Слайд 31 В треугольнике одна из сторон равна 10,
а косинус угла между ними равен .
Найдите площадь треугольника.
А
В
С
?
Задание 12
(№ 169860)
10
S-?
Подсказка (2):
12
20
Слайд 32 В треугольнике одна из сторон равна 10,
а тангенс угла между ними равен .
Найдите площадь треугольника.
А
В
С
?
Задание 12
(№ 169861)
10
S-?
Подсказка (3):
12
20
Слайд 33В прямоугольнике одна сторона 6,
а диагональ 10.
Найдите площадь прямоугольника.
А
В
С
Задание
(№ 169866)
6
Подсказка (3):
S-?
10
D
ВC
48
Слайд 34В прямоугольнике диагональ равна 10,
а угол между ней и одной из
Найдите площадь прямоугольника.
А
В
С
Задание 12
(№ 169867)
Подсказка (4):
S-?
10
D
300
ВC
АВ
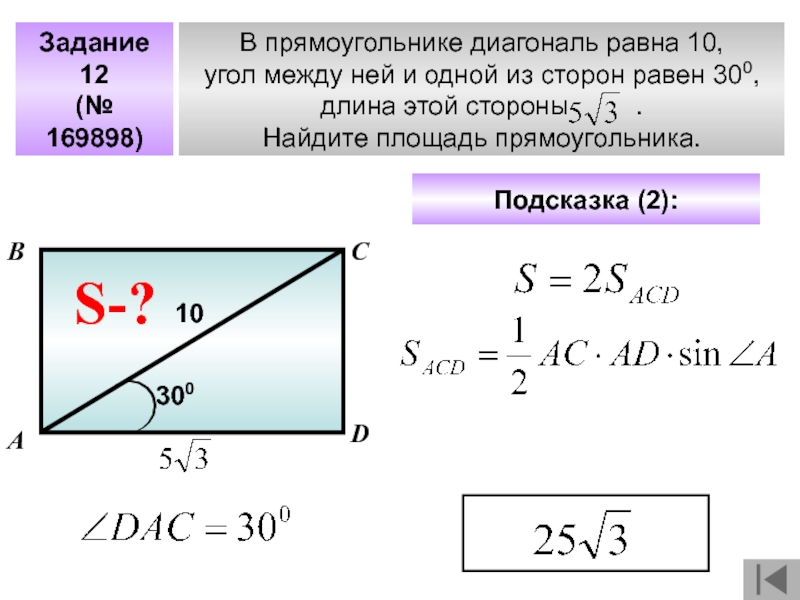
Слайд 35В прямоугольнике диагональ равна 10,
угол между ней и одной из
длина этой стороны .
Найдите площадь прямоугольника.
А
В
С
Задание 12
(№ 169898)
Подсказка (2):
S-?
10
D
300
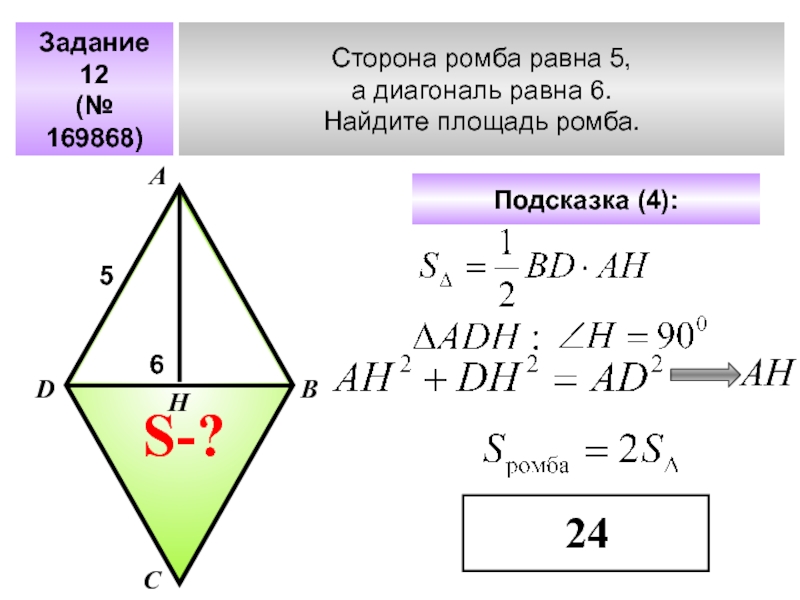
Слайд 36Задание 12
(№ 169868)
Сторона ромба равна 5,
а диагональ равна 6.
Найдите
А
В
С
D
Подсказка (4):
5
S-?
6
Н
АН
24
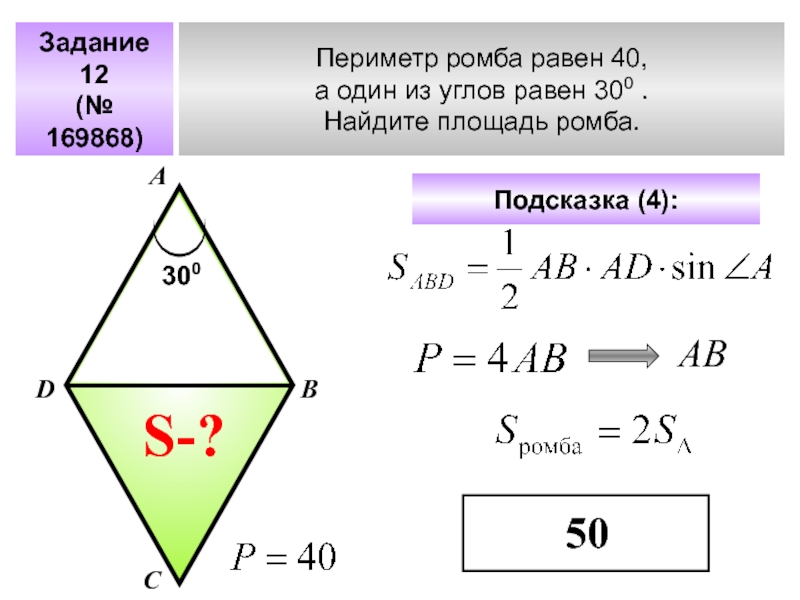
Слайд 37Задание 12
(№ 169868)
Периметр ромба равен 40,
а один из углов равен
Найдите площадь ромба.
А
В
С
D
Подсказка (4):
S-?
300
АВ
50
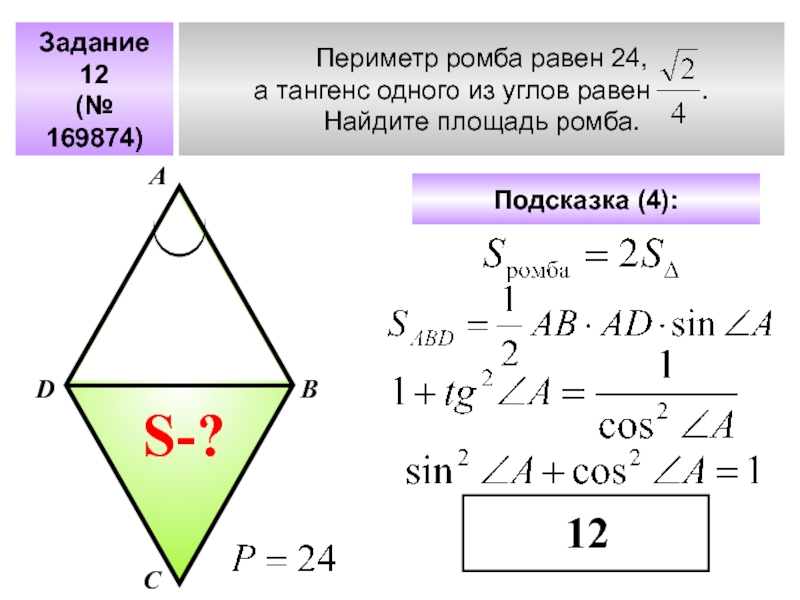
Слайд 38Задание 12
(№ 169874)
Периметр ромба равен 24,
а тангенс одного из углов
Найдите площадь ромба.
А
В
С
D
Подсказка (4):
S-?
12
Слайд 39Задание 12
(№ 169901)
В ромбе сторона равна 10,
одна из диагоналей —
лежащий напротив этой диагонали, равен 450.
Найдите площадь ромба.
А
В
С
D
Подсказка (2):
S-?
450
10
Слайд 40Задание 12
(№ 169906)
В ромбе сторона равна 10,
одна из диагоналей —
из которого выходит эта диагональ, равен 1500.
Найдите площадь ромба.
А
В
С
D
Подсказка (3):
10
S-?
1500
50
Слайд 41Задание 12
(№ 169876)
Одна из сторон параллелограмма равна 12,
другая равна 5,
Найдите площадь параллелограмма.
А
В
С
D
Подсказка (3):
12
5
450
S-?
Н
АН
Слайд 42Задание 12
(№ 169878)
Одна из сторон параллелограмма равна 12,
другая равна 5,
Найдите площадь параллелограмма.
А
В
С
D
Подсказка:
12
5
S-?
20
Слайд 43Задание 12
(№ 169879)
Одна из сторон параллелограмма равна 12,
другая равна 5,
Найдите площадь параллелограмма.
А
В
С
D
Подсказка (2):
12
5
S-?
20
Слайд 44Основания трапеции равны 18 и 12,
одна из боковых сторон равна
между ней и одним из оснований равен 1350.
Найдите площадь трапеции.
Задание 12
(№ 169881)
С
D
А
В
Подсказка (3):
60
S-?
12
18
1350
Н
ВН
Слайд 45Основания трапеции равны 18 и 12,
одна из боковых сторон равна
угла между ней и одним из оснований
равен . Найдите площадь трапеции.
Задание 12
(№ 169883)
С
D
А
В
Подсказка (5):
30
S-?
12
18
Н
ВН
6
Слайд 46Основания трапеции равны 18 и 12,
одна из боковых сторон равна
угла между ней и одним из оснований
равен . Найдите площадь трапеции.
Задание 12
(№ 169884)
С
D
А
В
Подсказка (5):
30
S-?
12
18
Н
ВН
6
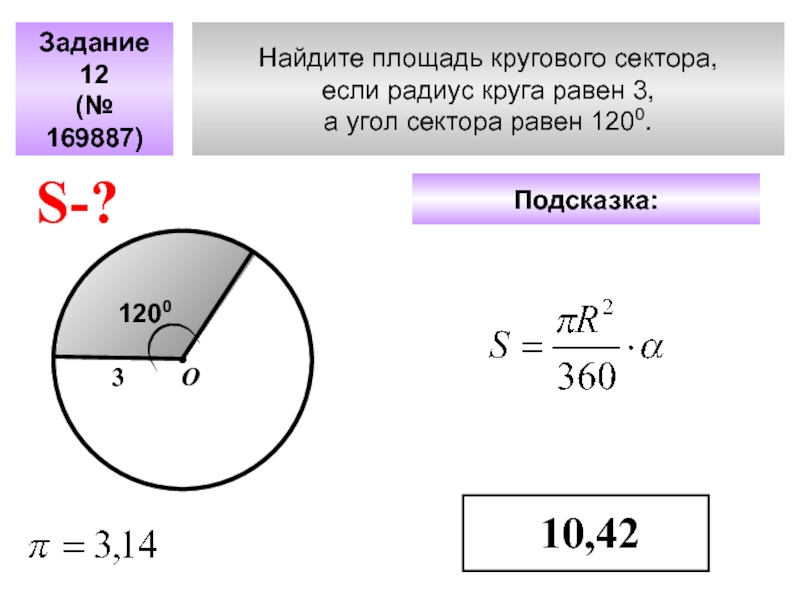
Слайд 48Найдите площадь кругового сектора,
если радиус круга равен 3,
а угол
Задание 12
(№ 169887)
Подсказка:
10,42
S-?
3
О
1200
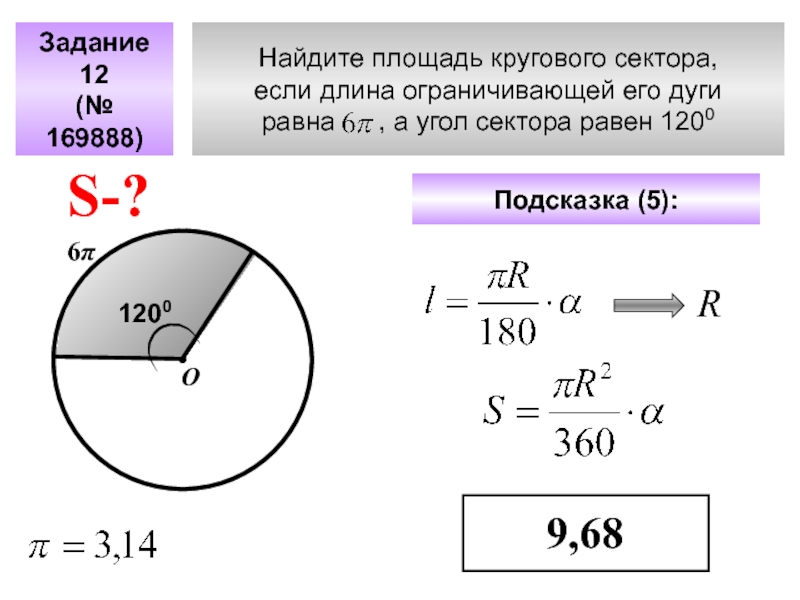
Слайд 49Найдите площадь кругового сектора,
если длина ограничивающей его дуги
равна
Задание 12
(№ 169888)
Подсказка (5):
9,68
S-?
6π
О
1200
R
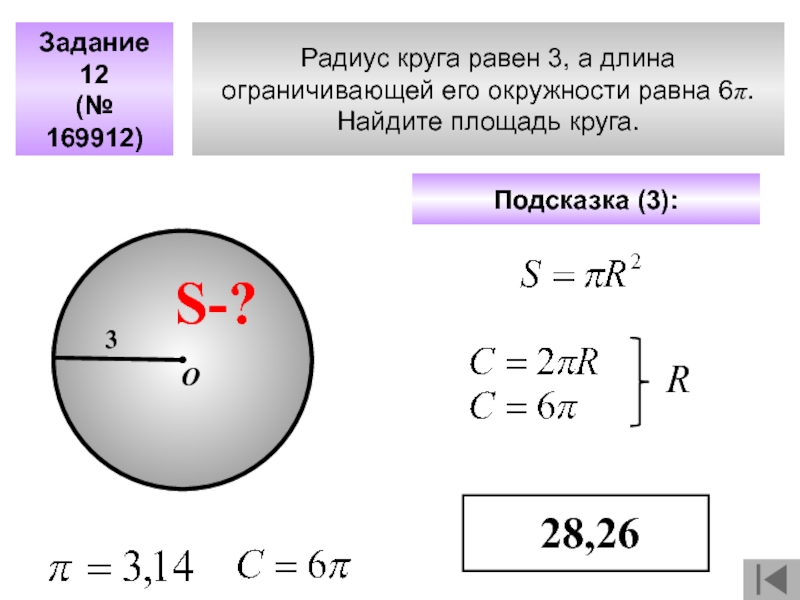
Слайд 50Радиус круга равен 3, а длина
ограничивающей его окружности равна 6π.
Найдите площадь круга.
Задание 12
(№ 169912)
Подсказка (3):
28,26
S-?
3
О
R