задачи чем-то напоминает трюки иллюзионистов - иногда, даже зная решение задачи, трудно понять, как можно было до него додуматься.
И.Д. Новиков
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Решение задач на нахождение боковой поверхности параллелепипеда и куба
Содержание
- 1. Презентация по математике на тему Решение задач на нахождение боковой поверхности параллелепипеда и куба
- 2. Призма Параллелепипед Прямоугольный параллелепипед Прямая призма Диагональ
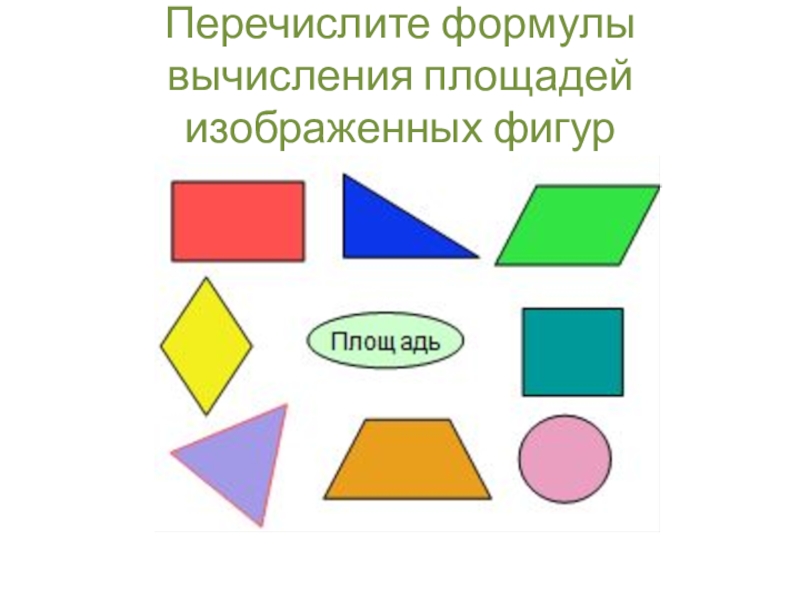
- 3. Перечислите формулы вычисления площадей изображенных фигур
- 4. Определите экономически выгодную упаковку. Сколько завод будет
- 5. 2. Сколько необходимо краски для покраски картонной
- 6. 3. Площадь поверхности куба равна 1568. Найдите
- 7. 5. Можно ли из кубиков размером 1×1×1
- 8. Домашнее задание
Призма Параллелепипед Прямоугольный параллелепипед Прямая призма Диагональ призмы Диагональ прямоугольного параллелепипеда Высота призмыДиагональное сечение Площадь боковой поверхности Площадь полной поверхности
Слайд 1Решение задач на нахождение боковой поверхности параллелепипеда и куба
Искусство решать геометрические
Слайд 2Призма
Параллелепипед
Прямоугольный параллелепипед
Прямая призма
Диагональ призмы
Диагональ прямоугольного параллелепипеда
Высота призмы
Диагональное сечение
Площадь боковой поверхности
Площадь полной поверхности
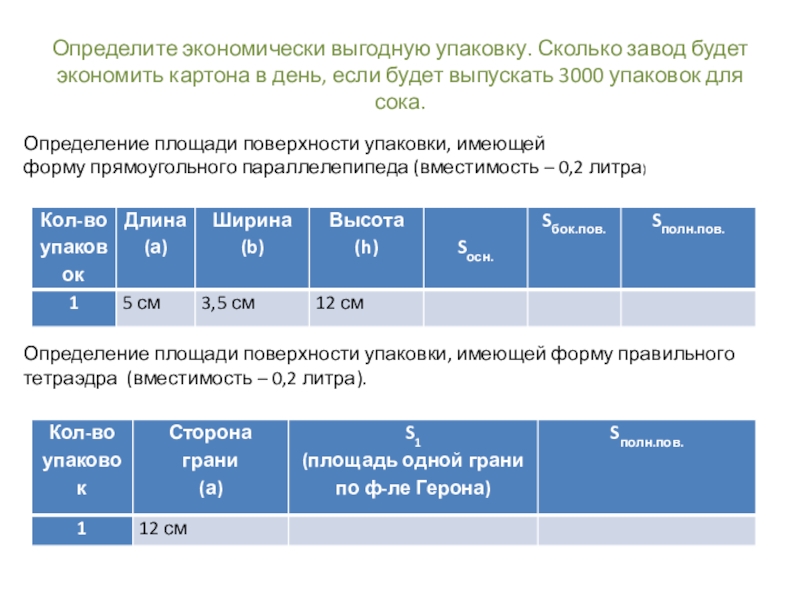
Слайд 4Определите экономически выгодную упаковку. Сколько завод будет экономить картона в день,
если будет выпускать 3000 упаковок для сока.
Определение площади поверхности упаковки, имеющей форму прямоугольного параллелепипеда (вместимость – 0,2 литра)
Определение площади поверхности упаковки, имеющей форму правильного тетраэдра (вместимость – 0,2 литра).
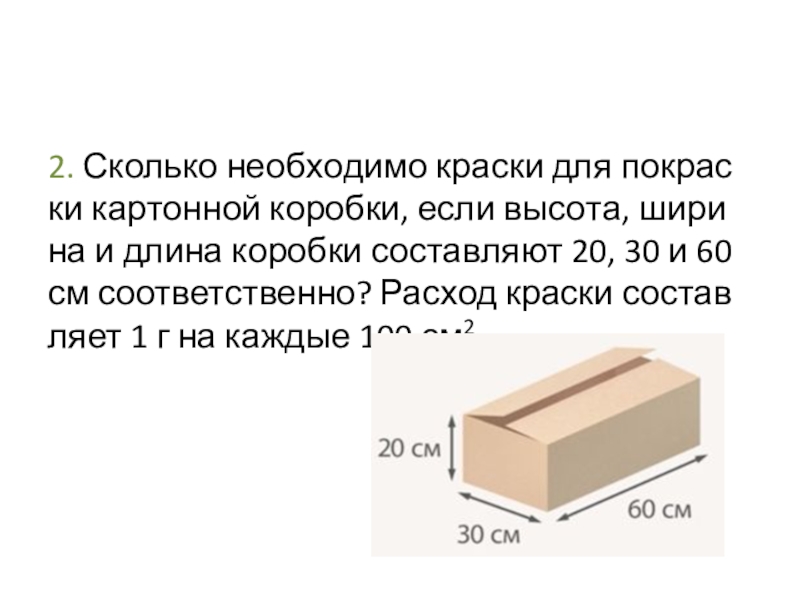
Слайд 52. Сколько необходимо краски для покраски картонной коробки, если высота, ширина
и длина коробки составляют 20, 30 и 60 см соответственно? Расход краски составляет 1 г на каждые 100 см2.
Слайд 63. Площадь поверхности куба равна 1568. Найдите его диагональ.
4. Два ребра
прямоугольного параллелепипеда, выходящие из одной вершины, равны 1 и 6. Площадь поверхности этого параллелепипеда равна 138. Найдите третье ребро, выходящее из той же вершины.
Слайд 75. Можно ли из кубиков размером 1×1×1 склеить многогранник, площадь поверхности
которого равна 2015? (Кубики приклеиваются так, что склеиваемые грани полностью примыкают друг к другу.)