основная общеобразовательная школа»
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Равнобедренный треугольник (7 класс)
Содержание
- 1. Презентация по математике на тему Равнобедренный треугольник (7 класс)
- 2. Тема урока: Равнобедренный треугольникАВСАВС
- 3. Этапы урокаОбъяснение нового материалаРешение задачСамостоятельная работаПодведение итогов урокаДомашнее задание
- 4. Объяснение нового материалаОпределение треугольникаОпределение равнобедренного треугольникаCвойство углов равнобедренного треугольникаСвойство медианы равнобедренного треугольника
- 5. Определение треугольникаТреугольником называется фигура, которая состоит из
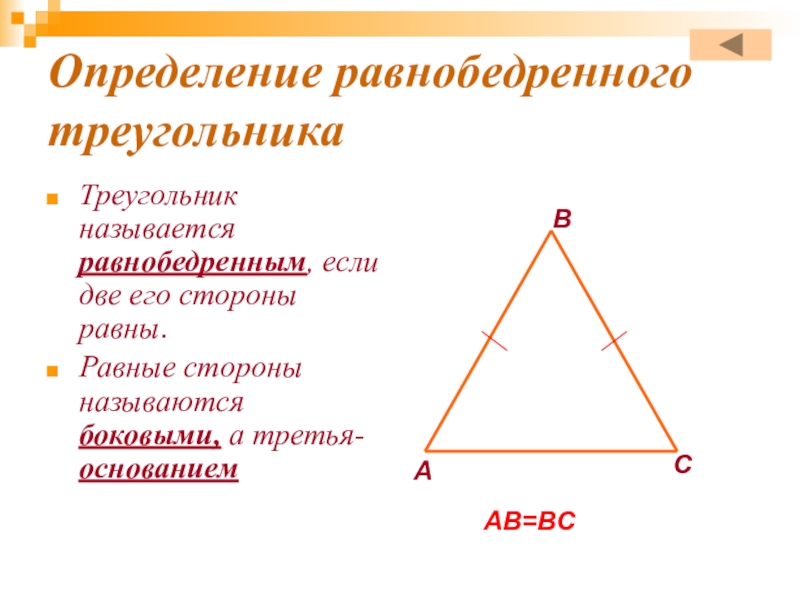
- 6. Определение равнобедренного треугольникаТреугольник называется равнобедренным, если две его стороны равны.Равные стороны называются боковыми, а третья- основаниемАСВАВ=ВС
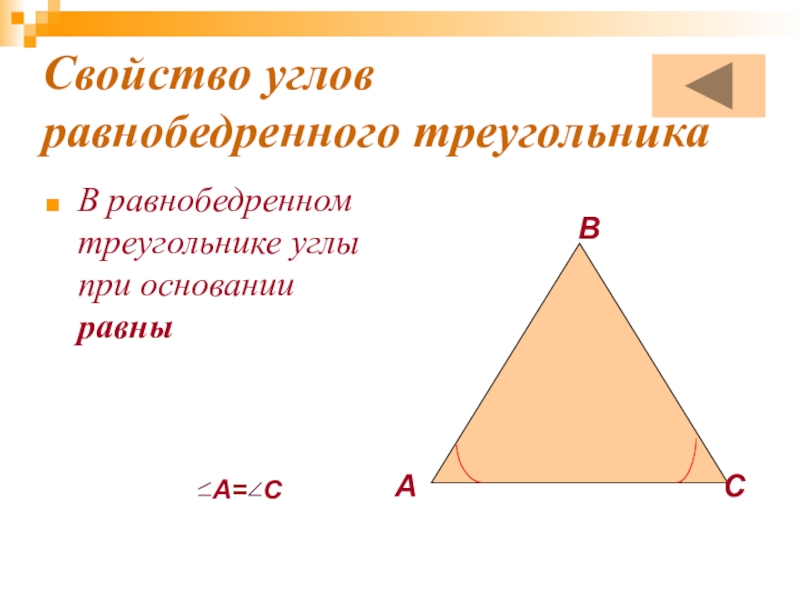
- 7. Свойство углов равнобедренного треугольникаВ равнобедренном треугольнике углы при основании равныАВСА= С
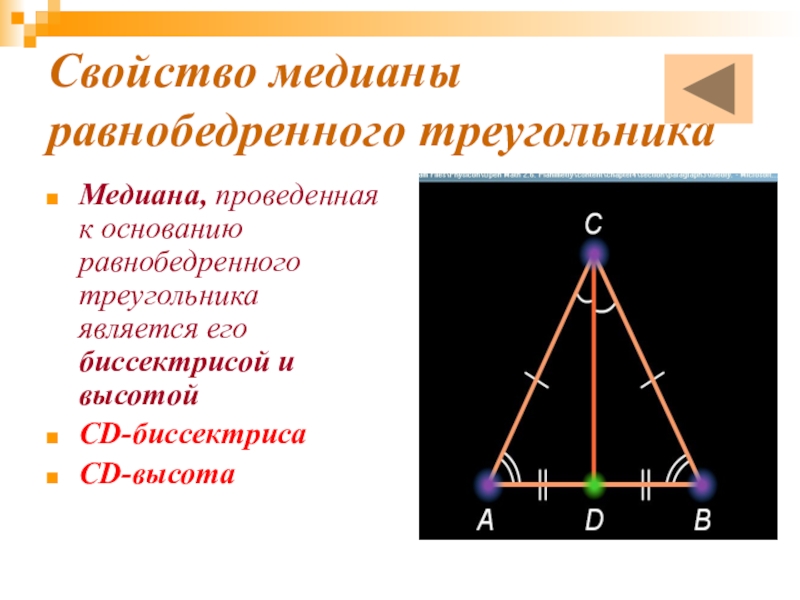
- 8. Свойство медианы равнобедренного треугольникаМедиана, проведенная к основанию равнобедренного треугольника является его биссектрисой и высотойCD-биссектрисаCD-высота
- 9. Упражнения№113№118№119№120(а)
- 10. ? Задачи Задача 1:В равнобедренном треугольнике сумма
- 11. Подведение итогов урокаЗадача 1Задача 2
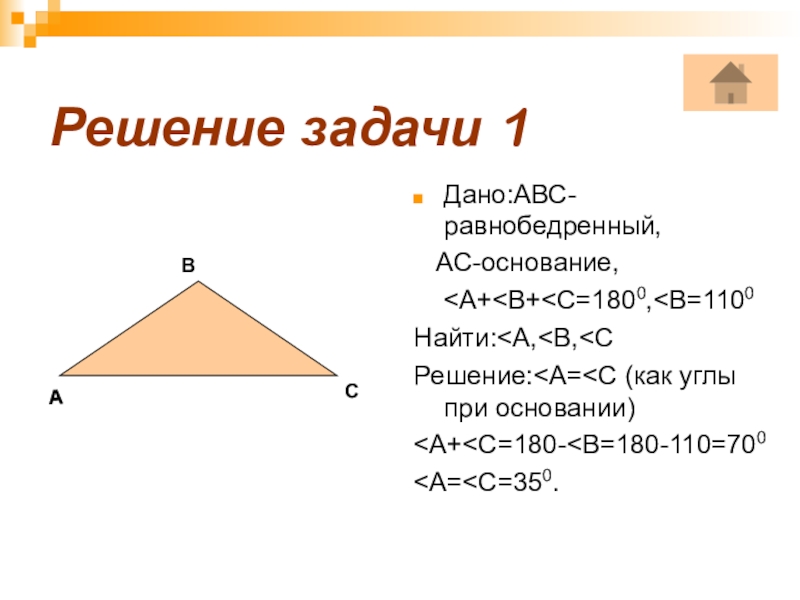
- 12. Решение задачи 1Дано:АВС-равнобедренный, АС-основание,
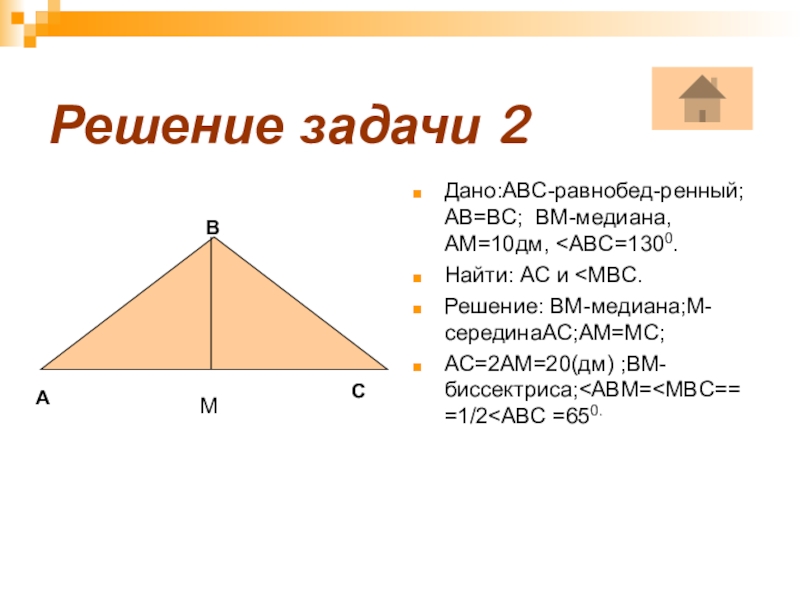
- 13. Решение задачи 2Дано:АВС-равнобед-ренный;АВ=ВС; ВМ-медиана,АМ=10дм,
- 14. п.п.16-18вопросы 5-13.Задачи №111, №112, №120(б)Домашнее заданиеп.п.16-18вопросы 5-13.Задачи №111, №112, №120(б)
- 15. При разработке презентации использованы:Открытая математика. ПланиметрияУчебник Геометрия7-9Изучение геометрии в 7-9 кл.
Тема урока: Равнобедренный треугольникАВСАВС
Слайд 3Этапы урока
Объяснение нового материала
Решение задач
Самостоятельная работа
Подведение итогов урока
Домашнее задание
Слайд 4
Объяснение нового материала
Определение треугольника
Определение равнобедренного треугольника
Cвойство углов равнобедренного треугольника
Свойство медианы равнобедренного
треугольника
Слайд 5Определение треугольника
Треугольником называется фигура, которая состоит из трех точек, не лежащих
на одной прямой, и трех отрезков, соединяющих их попарно.
Точки называются вершинами, отрезки-сторонами
Точки называются вершинами, отрезки-сторонами
Слайд 6Определение равнобедренного треугольника
Треугольник называется равнобедренным, если две его стороны равны.
Равные стороны
называются боковыми, а третья- основанием
А
С
В
АВ=ВС
Слайд 7Свойство углов равнобедренного треугольника
В равнобедренном треугольнике углы при основании равны
А
В
С
А= С
Слайд 8Свойство медианы равнобедренного треугольника
Медиана, проведенная к основанию равнобедренного треугольника является его
биссектрисой и высотой
CD-биссектриса
CD-высота
CD-биссектриса
CD-высота
Слайд 10? Задачи
Задача 1:В равнобедренном треугольнике сумма всех углов равна 180 0.Найдите
углы этого треугольника, если известно, что один из них равен 110 0.
Задача 2: В равнобедренном треугольнике АВС АВ=ВС, ВМ-медиана, АМ=10 дм, угол АВС =1300 .Найдите АС и угол МВС.
Задача 2: В равнобедренном треугольнике АВС АВ=ВС, ВМ-медиана, АМ=10 дм, угол АВС =1300 .Найдите АС и угол МВС.
для самостоятельного решения
Слайд 14п.п.16-18
вопросы 5-13.
Задачи №111, №112, №120(б)
Домашнее задание
п.п.16-18
вопросы 5-13.
Задачи №111, №112, №120(б)
Слайд 15При разработке презентации
использованы:
Открытая математика. Планиметрия
Учебник Геометрия7-9
Изучение геометрии в 7-9 кл.
