- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Равнобедренный треугольник(7 класс)
Содержание
- 1. Презентация по математике на тему Равнобедренный треугольник(7 класс)
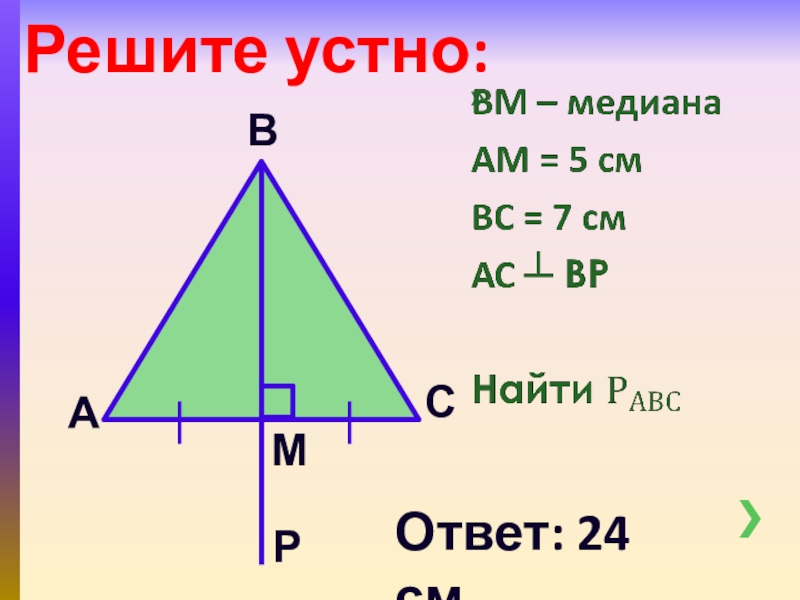
- 2. Решите устно:АМСВРОтвет: 24 см
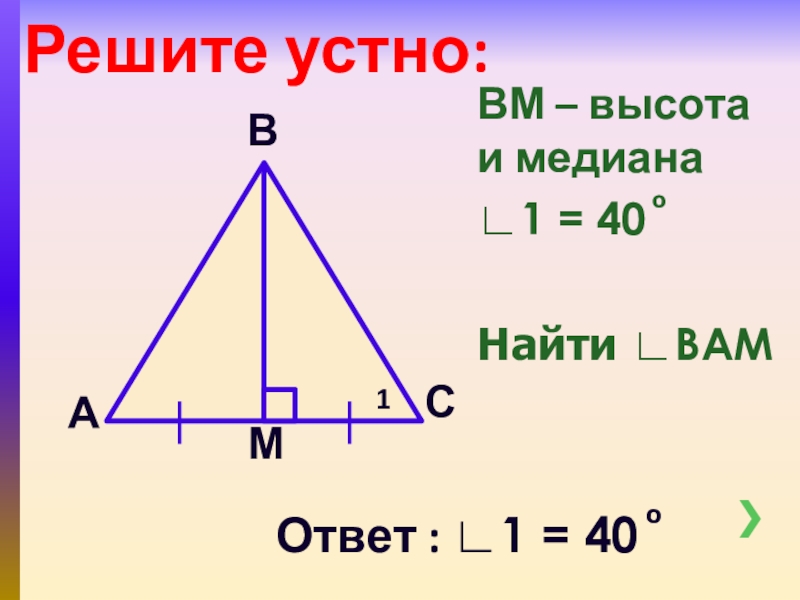
- 3. ВМ – высота и медиана∟1 = 40
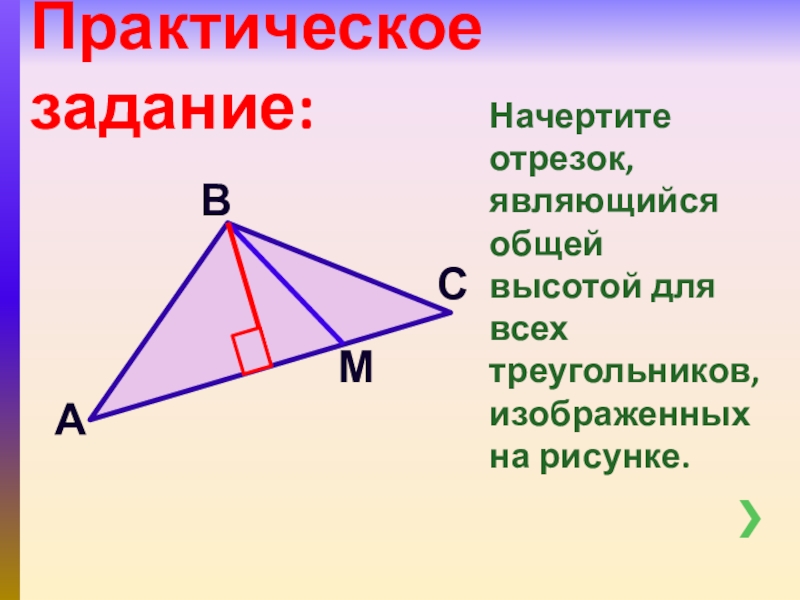
- 4. Практическое задание:Начертите отрезок, являющийся общей высотой для всех треугольников, изображенных на рисунке.АМСВ
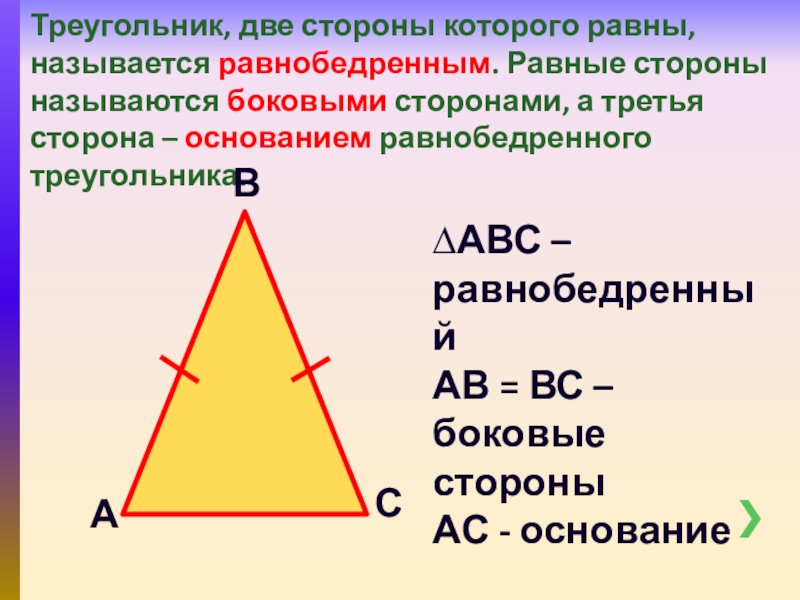
- 5. Треугольник, две стороны которого равны, называется равнобедренным.
- 6. Доказательство:Проведем биссектрису из угла В к основанию
- 7. Практическое задание:Постройте равнобедренный треугольник.Проведите биссектрисы углов.Будет ли
- 8. Практическое задание:1 вариант: Исследуйте медианы равнобедренного
- 9. Теорема: В равнобедренном треугольнике биссектриса проведенная к
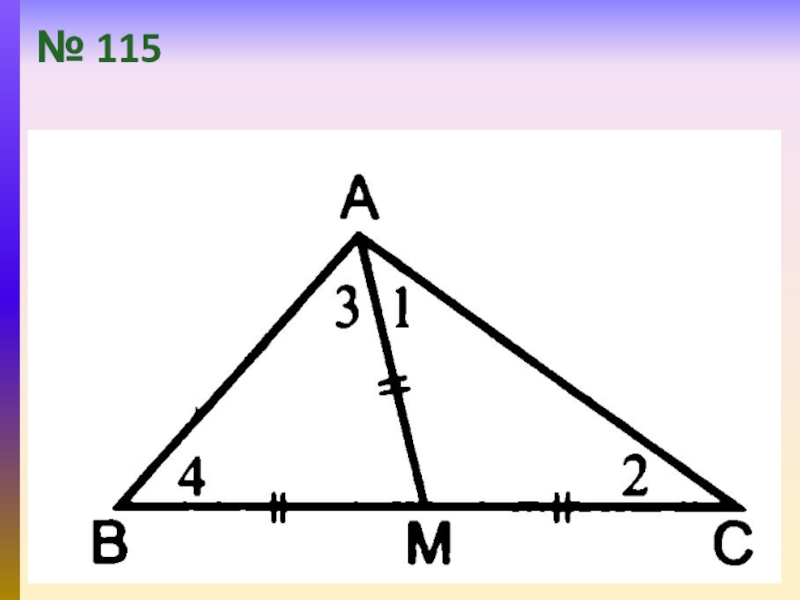
- 10. № 109№ 113№ 115
- 11. Домашнее задание:П 18№ 108, 110, 112.
- 12. Слайд 12
- 13. Доказательство:Проведем биссектрису из угла В к основанию
- 14. Теорема: В равнобедренном треугольнике биссектриса проведенная к
- 15. Слайд 15
- 16. Слайд 16
- 17. Задание:Является ли рвнобедренным треугольник АВС, если его
- 18. № 115
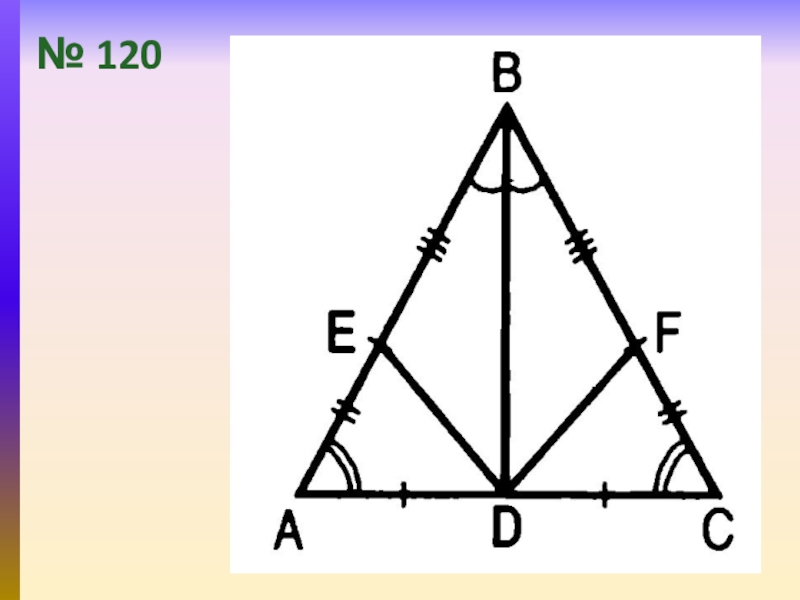
- 19. № 120
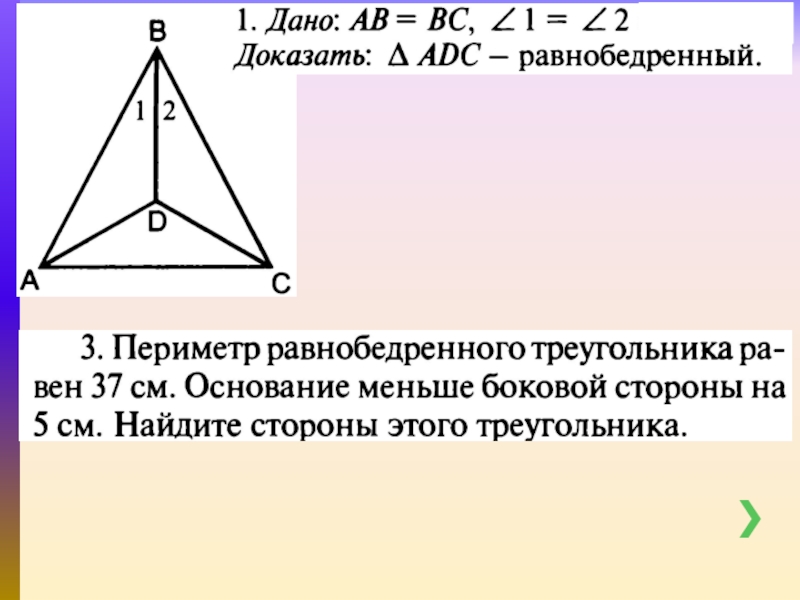
- 20. Слайд 20
Решите устно:АМСВРОтвет: 24 см
Слайд 4Практическое задание:
Начертите отрезок, являющийся общей высотой для всех треугольников, изображенных на
рисунке.
А
М
С
В
Слайд 5Треугольник, две стороны которого равны, называется равнобедренным. Равные стороны называются боковыми
сторонами, а третья сторона – основанием равнобедренного треугольника.
А
С
В
∆АВС – равнобедренный
АВ = ВС – боковые стороны
АС - основание
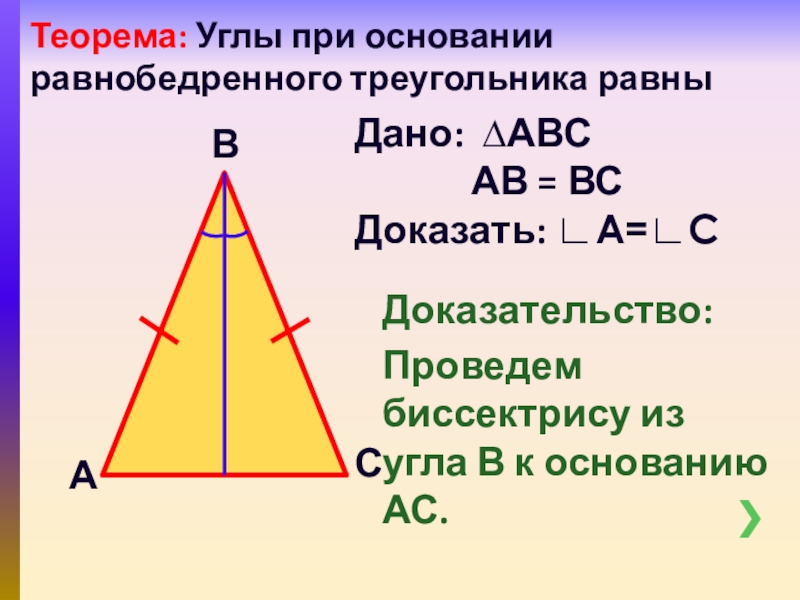
Слайд 6Доказательство:
Проведем биссектрису из угла В к основанию АС.
Теорема: Углы при основании
равнобедренного треугольника равны
А
С
В
Дано: ∆АВС
АВ = ВС
Доказать: ∟А=∟С
Слайд 7Практическое задание:
Постройте равнобедренный треугольник.
Проведите биссектрисы углов.
Будет ли биссектриса являться высотой, медианой
треугольника?
Все ли биссектрисы треугольника будут являться медианами и высотами?
Все ли биссектрисы треугольника будут являться медианами и высотами?
Слайд 8Практическое задание:
1 вариант:
Исследуйте медианы равнобедренного треугольника и перечислите их
свойства и особенности.
2 вариант:
Исследуйте высоты равнобедренного треугольника и перечислите их свойства и особенности.
2 вариант:
Исследуйте высоты равнобедренного треугольника и перечислите их свойства и особенности.
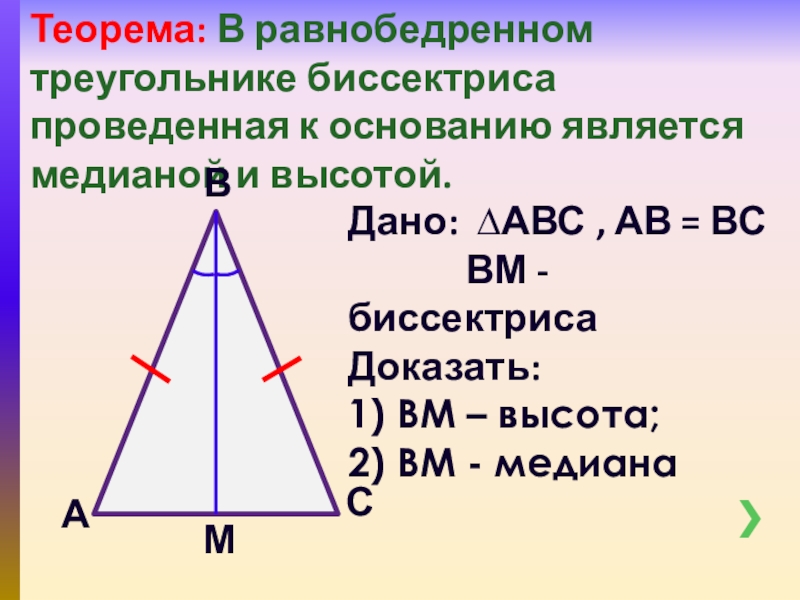
Слайд 9Теорема: В равнобедренном треугольнике биссектриса проведенная к основанию является медианой и
высотой.
А
С
В
Дано: ∆АВС , АВ = ВС
ВМ - биссектриса
Доказать:
1) ВМ – высота;
2) ВМ - медиана
М
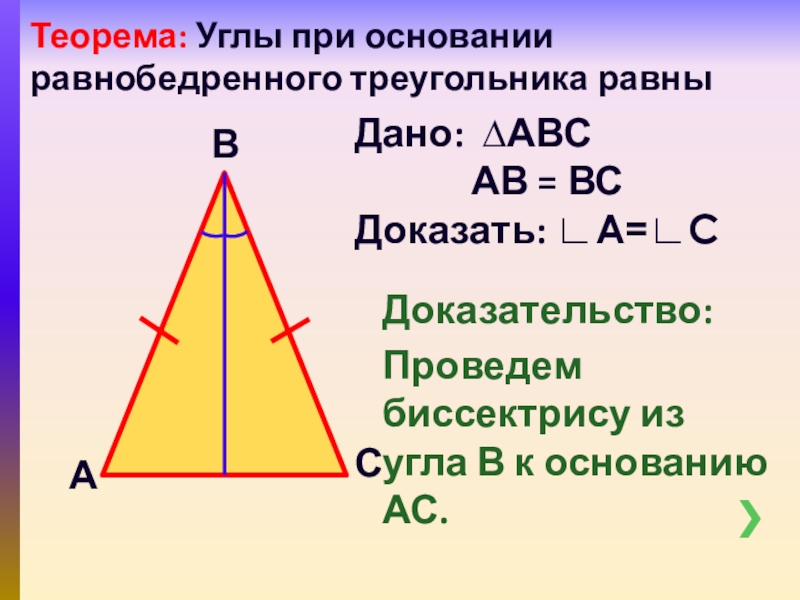
Слайд 13Доказательство:
Проведем биссектрису из угла В к основанию АС.
Теорема: Углы при основании
равнобедренного треугольника равны
А
С
В
Дано: ∆АВС
АВ = ВС
Доказать: ∟А=∟С
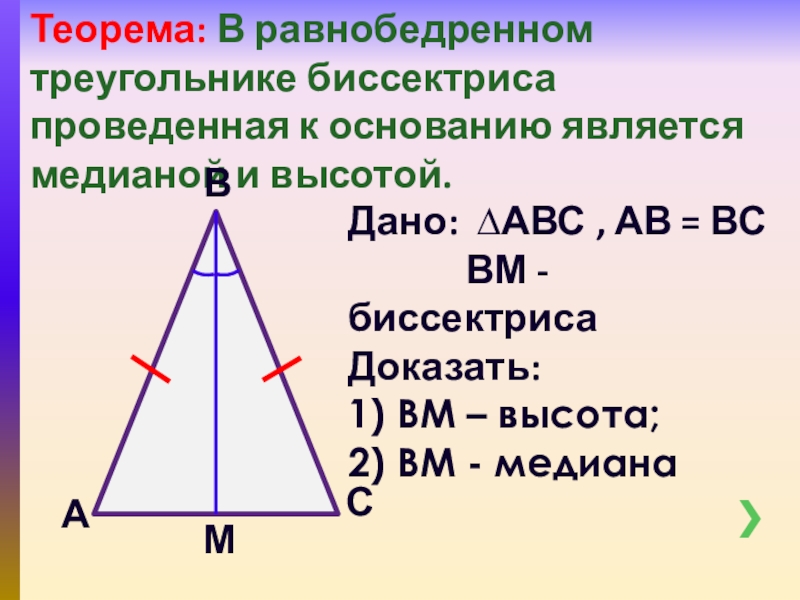
Слайд 14Теорема: В равнобедренном треугольнике биссектриса проведенная к основанию является медианой и
высотой.
А
С
В
Дано: ∆АВС , АВ = ВС
ВМ - биссектриса
Доказать:
1) ВМ – высота;
2) ВМ - медиана
М
Слайд 17Задание:
Является ли рвнобедренным треугольник АВС, если его периметр равен 47 см,
АВ = 19 см, ВС = 9 см? Объясните ответ.
Определите вид треугольника АВС, если АВ + ВС = АВ + АС = ВС + АС.
Является ли треугольник равнобедренным, если его углы равны 35 ⁰, 45 ⁰, 100 ⁰?
Определите вид треугольника АВС, если АВ + ВС = АВ + АС = ВС + АС.
Является ли треугольник равнобедренным, если его углы равны 35 ⁰, 45 ⁰, 100 ⁰?
