МКОУ Русскогвоздевская СОШ
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Призма 10 класс
Содержание
- 1. Презентация по математике на тему Призма 10 класс
- 2. Многогранник, поверхность которого состоит из двух равных
- 3. Слайд 3
- 4. Виды призм треугольная призма
- 5. Если боковое ребро призмы перпендикулярно плоскости ее
- 6. Свойства призмы:Основания призмы являются равными многоугольниками.Боковые грани
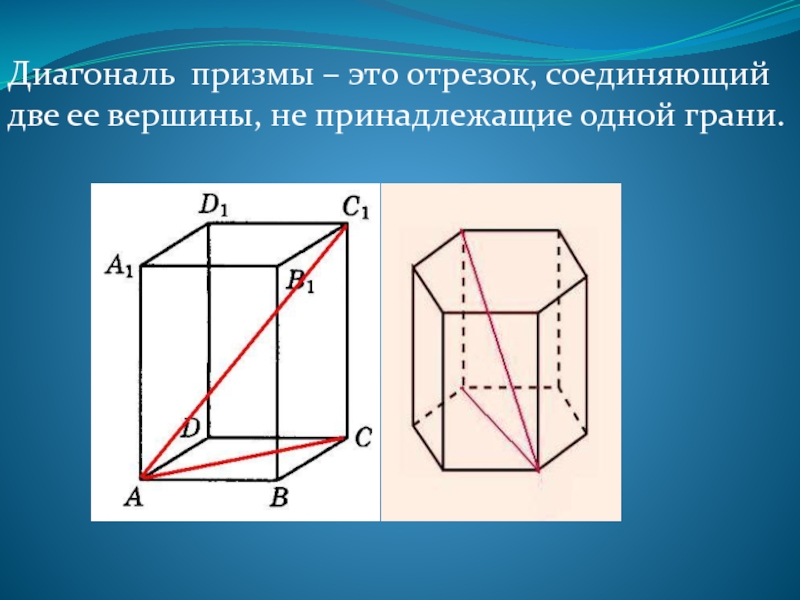
- 7. Диагональ призмы – это отрезок, соединяющий две ее вершины, не принадлежащие одной грани.
- 8. Сечение призмы1. Сечение призмы плоскостью, параллельной основанию. В
- 9. Симметрия правильной призмы1. Центр симметрии при четном числе
- 10. Симметрия правильной призмы
- 11. Дано: Сторона основания правильной треугольной призмы равна
- 12. Спасибо за внимание!!!
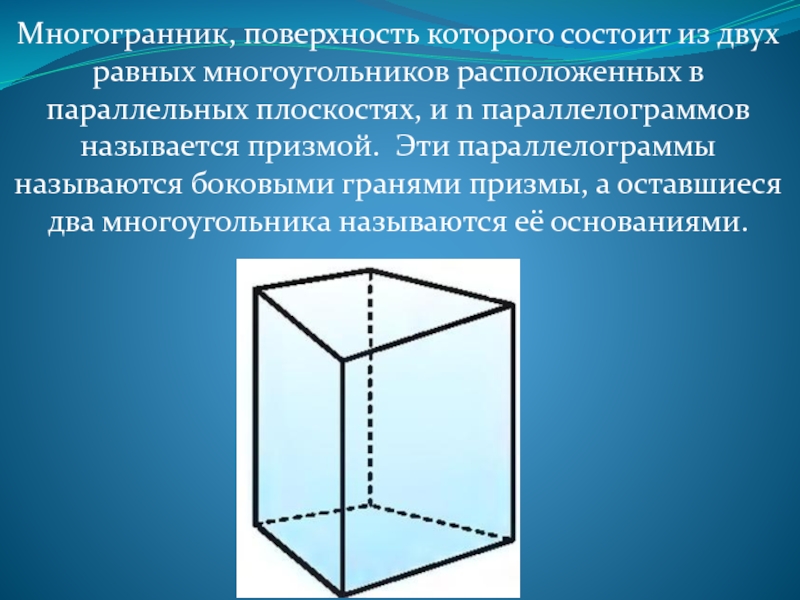
Многогранник, поверхность которого состоит из двух равных многоугольников расположенных в параллельных плоскостях, и n параллелограммов называется призмой. Эти параллелограммы называются боковыми гранями призмы, а оставшиеся два многоугольника называются её основаниями.
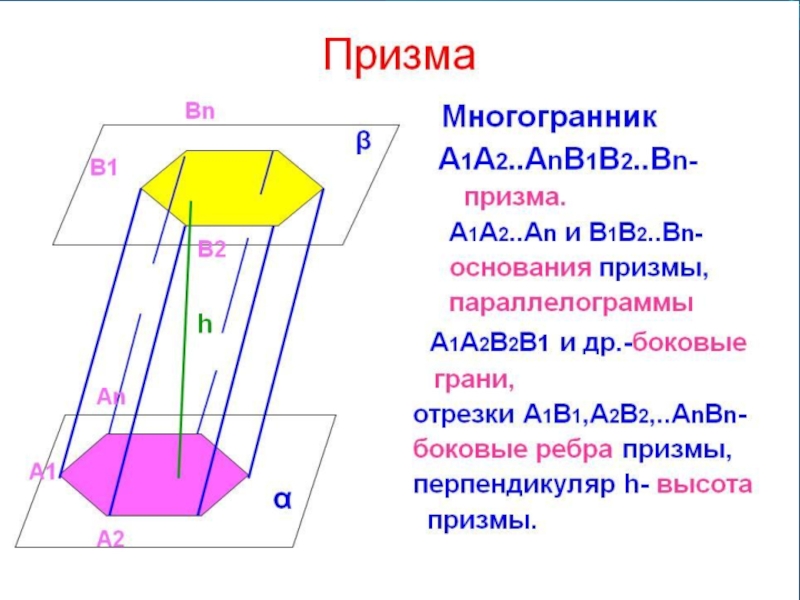
Слайд 1Призма. Элементы
призмы. Площадь боковой
и полной
поверхности призмы.
Богачева Нина
Владимировна
Слайд 2Многогранник, поверхность которого состоит из двух равных многоугольников расположенных в параллельных
плоскостях, и n параллелограммов называется призмой. Эти параллелограммы называются боковыми гранями призмы, а оставшиеся два многоугольника называются её основаниями.
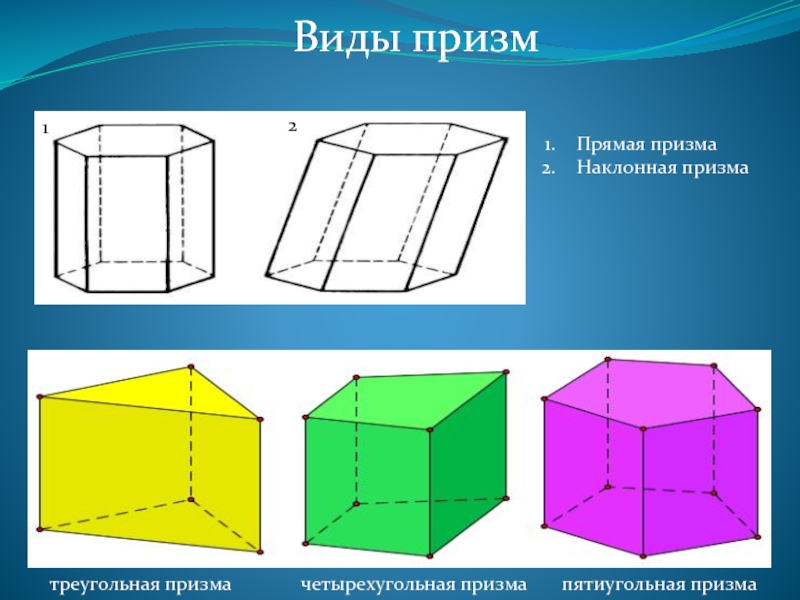
Слайд 4Виды призм
треугольная призма
четырехугольная призма пятиугольная призма
1
2
Прямая призма
Наклонная призма
Слайд 5Если боковое ребро призмы перпендикулярно плоскости ее основания, то такую призму
называют прямой; если боковое ребро призмы перпендикулярно плоскости ее основания, то такую призму называют наклонной. У прямой призмы боковые грани - прямоугольники. Перпендикуляр к плоскостям оснований, концы которого принадлежат этим плоскостям, называют высотой призмы.
Слайд 6Свойства призмы:
Основания призмы являются равными многоугольниками.
Боковые грани призмы являются параллелограммами.
Боковые ребра
призмы параллельны и равны.
Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания. Площадь боковой поверхности прямой призмы S=P*h, где P — периметр основания призмы, h — высота призмы.
Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания. Площадь боковой поверхности прямой призмы S=P*h, где P — периметр основания призмы, h — высота призмы.
Слайд 8Сечение призмы
1. Сечение призмы плоскостью, параллельной основанию. В сечении образуется многоугольник, равный
многоугольнику, лежащему в основании.
2. Сечение призмы плоскостью, проходящей через два не соседних боковых ребра. В сечении образуется параллелограмм. Такое сечение называется диагональным сечением призмы. В некоторых случаях может получаться ромб, прямоугольник или квадрат.
2. Сечение призмы плоскостью, проходящей через два не соседних боковых ребра. В сечении образуется параллелограмм. Такое сечение называется диагональным сечением призмы. В некоторых случаях может получаться ромб, прямоугольник или квадрат.
Слайд 9Симметрия правильной призмы
1. Центр симметрии при четном числе сторон основания — точка пересечения
диагоналей правильной призмы.
2. Плоскости симметрии: плоскость, проходящая через середины боковых ребер; при четном числе сторон основания — плоскости, проходящие через противолежащие ребра.
3. Оси симметрии: при четном числе сторон основания — ось симметрии, проходящая через центры оснований, и оси симметрии, проходящие через точки пересечения диагоналей противолежащих боковых граней.
2. Плоскости симметрии: плоскость, проходящая через середины боковых ребер; при четном числе сторон основания — плоскости, проходящие через противолежащие ребра.
3. Оси симметрии: при четном числе сторон основания — ось симметрии, проходящая через центры оснований, и оси симметрии, проходящие через точки пересечения диагоналей противолежащих боковых граней.
Слайд 11Дано: Сторона основания правильной треугольной призмы равна 8 см, боковое ребро
- 6 см. Найдите Sсеч, проходящего через сторону верхнего основания и противолежащую вершину нижнего основания.
Решение: Треугольник A1B1C1 - равнобедренный(A1B=C1B как диагональ равных граней)
1)Рассмотрим треугольник BCC1– прямоугольный
BC12=BС2+CC12
BC1= √ 64+36=10 см
2) Рассмотрим треугольник BMC1– прямоугольный
BC12=BM2+MC12
BM2=BC12-MC12
BM2=100-16=84
BM= √ 84=2 √ 21 см
3) Sсеч=12 A1C1*BM= 12*2√ 21 см*8=8 √ 21
Решение: Треугольник A1B1C1 - равнобедренный(A1B=C1B как диагональ равных граней)
1)Рассмотрим треугольник BCC1– прямоугольный
BC12=BС2+CC12
BC1= √ 64+36=10 см
2) Рассмотрим треугольник BMC1– прямоугольный
BC12=BM2+MC12
BM2=BC12-MC12
BM2=100-16=84
BM= √ 84=2 √ 21 см
3) Sсеч=12 A1C1*BM= 12*2√ 21 см*8=8 √ 21
Задача по теме «Призма»