Математика
Студент: Максимов Артур
Группа: 17 ДМ
Преподаватель: Сытенкова Татьяна Викторовна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему : Поверхности 2 порядка
Содержание
- 1. Презентация по математике на тему : Поверхности 2 порядка
- 2. Поверхности второго порядка
- 3. 9) — эллиптический цилиндр,10) — мнимый эллиптический
- 4. Поверхность второго порядка, рассматриваемая как геометрический объект,
- 5. Эллипсоид Каноническое
- 6. 1. Однополостный
- 7. 2. Двуполостный
- 8. Параболоиды 1. Эллиптический
- 9. Параболоиды 2. Гиперболический
- 10. Конус и цилиндры второго порядка
- 11. Конус и цилиндры второго порядка
- 12. Конус и цилиндры второго порядка
- 13. Конус и цилиндры второго порядка
- 14. ЗадачиОпределите вид цилиндрической поверхности F, найдите уравнение
- 15. Определите
- 16. 3.
Поверхности второго порядка Поверхностью второго порядка S называется геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида: где по крайней мере один из коэффициентов отличен от нуля. Это уравнение называют общим
Слайд 2Поверхности второго порядка
Поверхностью второго порядка S
называется геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида:
где по крайней мере один из коэффициентов отличен от нуля. Это уравнение называют общим уравнением поверхности второго порядка S (обозначим это ур-е 1), а систему координат Oxyz называют общей системой координат.
Теорема: Для произвольной поверхности S, заданной общим уравнением существует такая декартова прямоугольная система координат что в этой системе поверхность S имеет уравнение одного из следующих семнадцати канонических видов.
1) — эллипсоид,
2) — мнимый эллипсоид,
3) — однополостный гиперболоид,
4) — двуполостный гиперболоид,
5) — конус,
6) — мнимый конус (точка),
7) — эллиптический параболоид,
8) — гиперболический параболоид,
где по крайней мере один из коэффициентов отличен от нуля. Это уравнение называют общим уравнением поверхности второго порядка S (обозначим это ур-е 1), а систему координат Oxyz называют общей системой координат.
Теорема: Для произвольной поверхности S, заданной общим уравнением существует такая декартова прямоугольная система координат что в этой системе поверхность S имеет уравнение одного из следующих семнадцати канонических видов.
1) — эллипсоид,
2) — мнимый эллипсоид,
3) — однополостный гиперболоид,
4) — двуполостный гиперболоид,
5) — конус,
6) — мнимый конус (точка),
7) — эллиптический параболоид,
8) — гиперболический параболоид,
Слайд 39) — эллиптический цилиндр,
10) — мнимый эллиптический цилиндр,
11) — две мнимые
пересекающиеся плоскости (ось O'Z),
12) — гиперболический цилиндр,
13) — две пересекающиеся плоскости,
14) — параболический цилиндр,
15) — две параллельные плоскости,
16) — две мнимые параллельные плоскости,
17) — две совпадающие плоскости (плоскость XOZ).
В выше перечисленных уравнениях a, b, c, p — положительные параметры. Систему координат называют канонической.
12) — гиперболический цилиндр,
13) — две пересекающиеся плоскости,
14) — параболический цилиндр,
15) — две параллельные плоскости,
16) — две мнимые параллельные плоскости,
17) — две совпадающие плоскости (плоскость XOZ).
В выше перечисленных уравнениях a, b, c, p — положительные параметры. Систему координат называют канонической.
Слайд 4 Поверхность второго порядка, рассматриваемая как геометрический объект, не
меняется, если от
данной декартовой прямоугольной системы координат перейти к другой
декартовой системе координат. Отметим, что исходное уравнение (1) и уравнение,
полученное после преобразования координат, алгебраически эквивалентны.
Классификация центральных поверхностей. Пусть S — центральная поверхность
второго порядка. Перенесем начало координат в центр этой поверхности, а затем
произведем стандартное упрощение уравнения этой поверхности. В результате
уравнение поверхности примет вид: a11х2 + а22у2 + a33z2 + а44 =0 (2)
Так как инвариант I3 для центральной поверхности отличен от нуля и его значение,
вычисленное для уравнения (2) , равно a11 • а22 • a33 , то коэффициенты a11,а22, a33
удовлетворяют условию :
Возможны следующие случаи :
1. Коэффициенты a11 ,а22 , a33 одного знака, а коэффициент а44 отличен от нуля. В этом
случае поверхность S называется эллипсоидом.
Обычно уравнение эллипсоида записывают в канонической форме:
2. Если из четырех коэффициентов a11 ,а22 , a33 , а44 два одного знака, а два других—
противоположного. В этом случае поверхность S называется однополостным гиперболоидом.
3. Если знак одного из первых трех коэффициентов a11, а22, a33, а44 противоположен знаку
остальных коэффициентов. В этом случае поверхность S называется двуполостным
гиперболоидом.
декартовой системе координат. Отметим, что исходное уравнение (1) и уравнение,
полученное после преобразования координат, алгебраически эквивалентны.
Классификация центральных поверхностей. Пусть S — центральная поверхность
второго порядка. Перенесем начало координат в центр этой поверхности, а затем
произведем стандартное упрощение уравнения этой поверхности. В результате
уравнение поверхности примет вид: a11х2 + а22у2 + a33z2 + а44 =0 (2)
Так как инвариант I3 для центральной поверхности отличен от нуля и его значение,
вычисленное для уравнения (2) , равно a11 • а22 • a33 , то коэффициенты a11,а22, a33
удовлетворяют условию :
Возможны следующие случаи :
1. Коэффициенты a11 ,а22 , a33 одного знака, а коэффициент а44 отличен от нуля. В этом
случае поверхность S называется эллипсоидом.
Обычно уравнение эллипсоида записывают в канонической форме:
2. Если из четырех коэффициентов a11 ,а22 , a33 , а44 два одного знака, а два других—
противоположного. В этом случае поверхность S называется однополостным гиперболоидом.
3. Если знак одного из первых трех коэффициентов a11, а22, a33, а44 противоположен знаку
остальных коэффициентов. В этом случае поверхность S называется двуполостным
гиперболоидом.
Слайд 5Эллипсоид
Каноническое уравнение эллипсоида имеет вид:
Свойства эллипсоида:
Эллипсоид обладает
1) Центральной симметрией относительно начала координат,
2) Осевой симметрией относительно координатных осей,
3) Плоскостной симметрией относительно начала координат.
В сечении эллипсоида плоскостью, перпендикулярной
любой из координатных осей, получается эллипс.
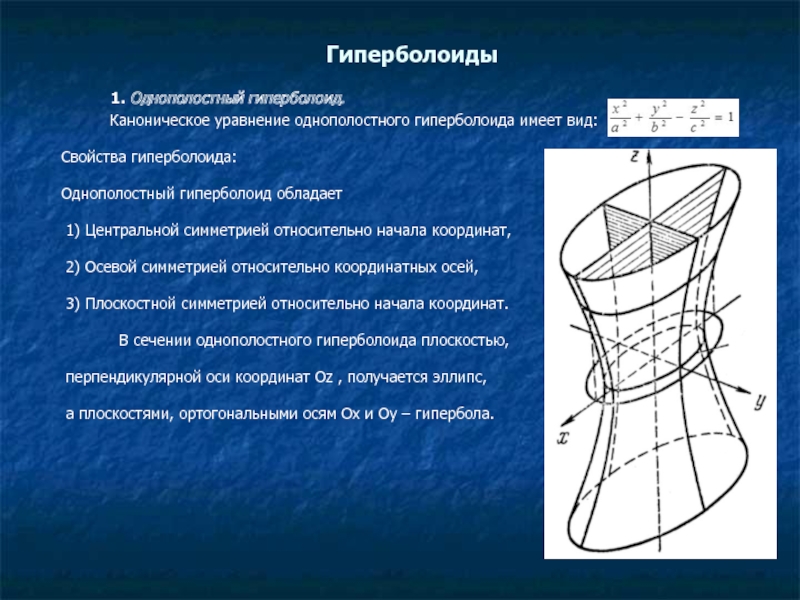
Слайд 6 1. Однополостный гиперболоид.
Каноническое уравнение однополостного гиперболоида имеет вид:
Свойства гиперболоида:
Однополостный гиперболоид обладает
1) Центральной симметрией относительно начала координат,
2) Осевой симметрией относительно координатных осей,
3) Плоскостной симметрией относительно начала координат.
В сечении однополостного гиперболоида плоскостью,
перпендикулярной оси координат Oz , получается эллипс,
а плоскостями, ортогональными осям Ox и Oy – гипербола.
Свойства гиперболоида:
Однополостный гиперболоид обладает
1) Центральной симметрией относительно начала координат,
2) Осевой симметрией относительно координатных осей,
3) Плоскостной симметрией относительно начала координат.
В сечении однополостного гиперболоида плоскостью,
перпендикулярной оси координат Oz , получается эллипс,
а плоскостями, ортогональными осям Ox и Oy – гипербола.
Гиперболоиды
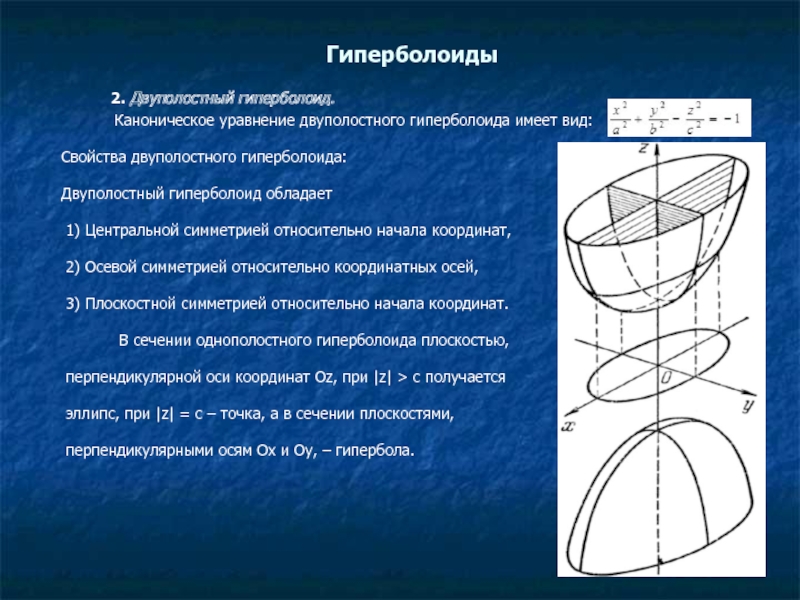
Слайд 7 2. Двуполостный гиперболоид.
Каноническое уравнение двуполостного гиперболоида имеет вид:
Свойства двуполостного гиперболоида:
Двуполостный гиперболоид обладает
1) Центральной симметрией относительно начала координат,
2) Осевой симметрией относительно координатных осей,
3) Плоскостной симметрией относительно начала координат.
В сечении однополостного гиперболоида плоскостью,
перпендикулярной оси координат Oz, при |z| > c получается
эллипс, при |z| = c – точка, а в сечении плоскостями,
перпендикулярными осям Ox и Oy, – гипербола.
Свойства двуполостного гиперболоида:
Двуполостный гиперболоид обладает
1) Центральной симметрией относительно начала координат,
2) Осевой симметрией относительно координатных осей,
3) Плоскостной симметрией относительно начала координат.
В сечении однополостного гиперболоида плоскостью,
перпендикулярной оси координат Oz, при |z| > c получается
эллипс, при |z| = c – точка, а в сечении плоскостями,
перпендикулярными осям Ox и Oy, – гипербола.
Гиперболоиды
Слайд 8Параболоиды
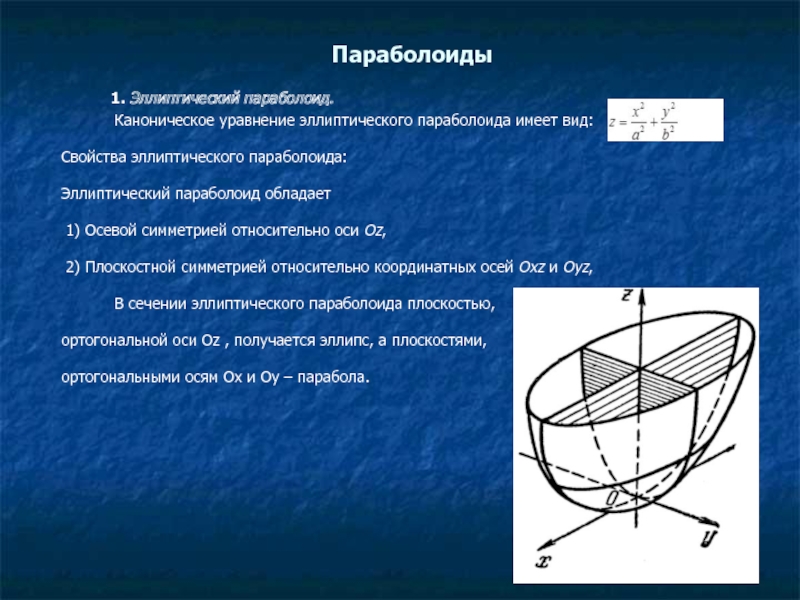
1. Эллиптический параболоид.
Каноническое уравнение эллиптического параболоида имеет вид:
Свойства эллиптического параболоида:
Эллиптический параболоид обладает
1) Осевой симметрией относительно оси Oz,
2) Плоскостной симметрией относительно координатных осей Oxz и Oyz,
В сечении эллиптического параболоида плоскостью,
ортогональной оси Oz , получается эллипс, а плоскостями,
ортогональными осям Ox и Oy – парабола.
Свойства эллиптического параболоида:
Эллиптический параболоид обладает
1) Осевой симметрией относительно оси Oz,
2) Плоскостной симметрией относительно координатных осей Oxz и Oyz,
В сечении эллиптического параболоида плоскостью,
ортогональной оси Oz , получается эллипс, а плоскостями,
ортогональными осям Ox и Oy – парабола.
Слайд 9Параболоиды
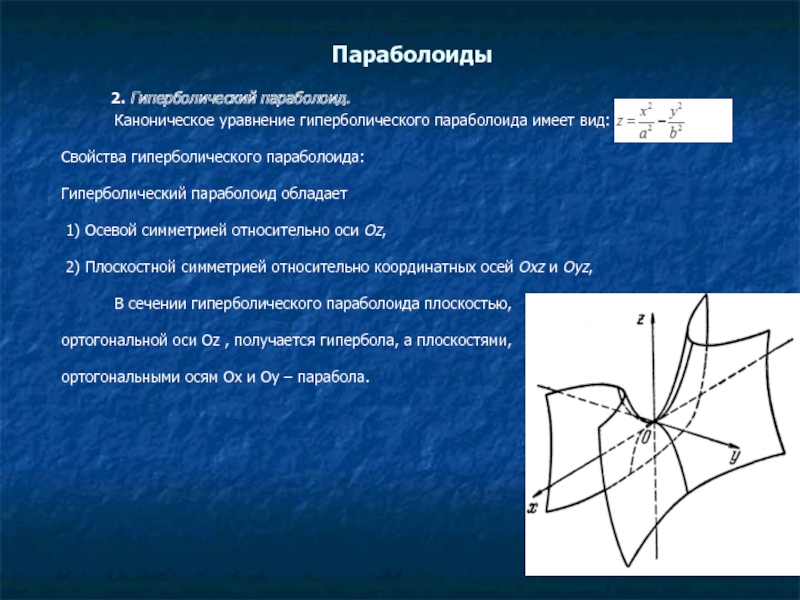
2. Гиперболический параболоид.
Каноническое уравнение гиперболического параболоида имеет вид:
Свойства гиперболического параболоида:
Гиперболический параболоид обладает
1) Осевой симметрией относительно оси Oz,
2) Плоскостной симметрией относительно координатных осей Oxz и Oyz,
В сечении гиперболического параболоида плоскостью,
ортогональной оси Oz , получается гипербола, а плоскостями,
ортогональными осям Ox и Oy – парабола.
Свойства гиперболического параболоида:
Гиперболический параболоид обладает
1) Осевой симметрией относительно оси Oz,
2) Плоскостной симметрией относительно координатных осей Oxz и Oyz,
В сечении гиперболического параболоида плоскостью,
ортогональной оси Oz , получается гипербола, а плоскостями,
ортогональными осям Ox и Oy – парабола.
Слайд 10Конус и цилиндры второго порядка
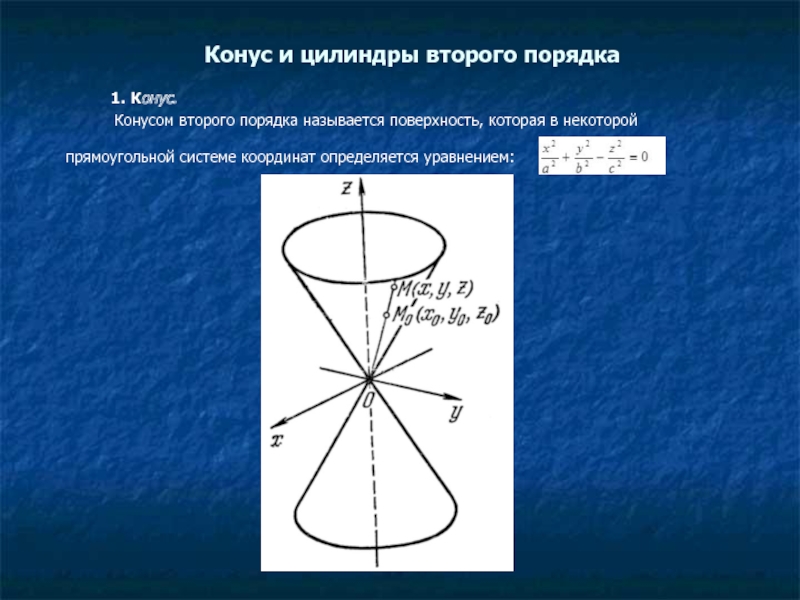
1. Конус.
Конусом второго порядка называется поверхность, которая в некоторой
прямоугольной системе координат определяется уравнением:
Слайд 11Конус и цилиндры второго порядка
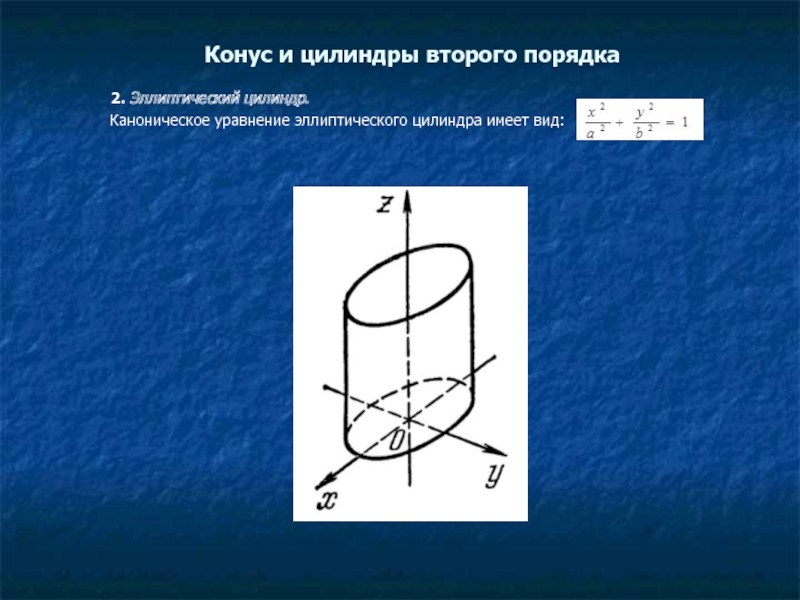
2. Эллиптический
цилиндр.
Каноническое уравнение эллиптического цилиндра имеет вид:
Каноническое уравнение эллиптического цилиндра имеет вид:
Слайд 12Конус и цилиндры второго порядка
3. Гиперболический
цилиндр.
Каноническое уравнение гиперболического цилиндра имеет вид:
Каноническое уравнение гиперболического цилиндра имеет вид:
Слайд 13Конус и цилиндры второго порядка
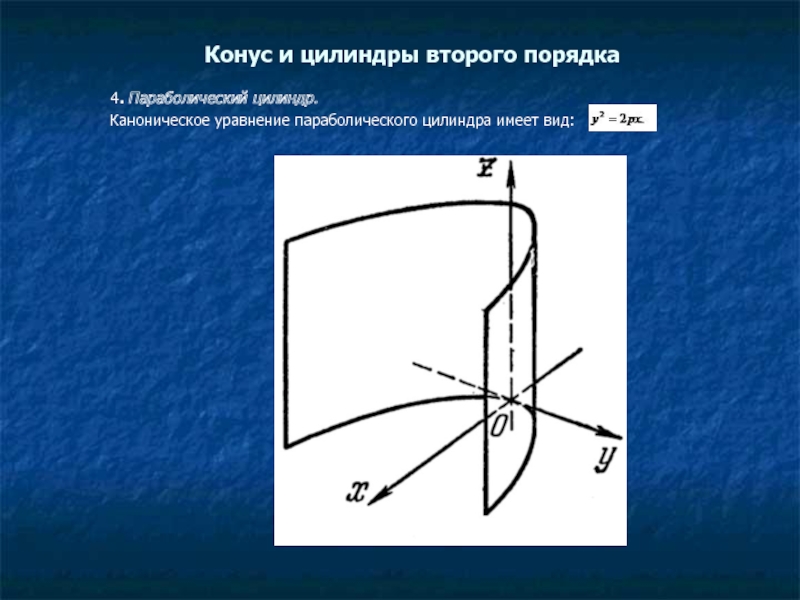
4. Параболический
цилиндр.
Каноническое уравнение параболического цилиндра имеет вид:
Каноническое уравнение параболического цилиндра имеет вид:
Слайд 14Задачи
Определите вид цилиндрической поверхности F, найдите уравнение её
направляющей y, направление образующих
и изобразите эту поверхность, если в
прямоугольной системе координат поверхность F задана уравнением F:
Решение: Приведем уравнение поверхности F к каноническому виду :
Следовательно, F – эллиптический цилиндр. Его направляющая y задается
уравнением y: (Она лежит в плоскости Oxz), а образующие параллельные
координатному вектору . Поверхность F изображена на рисунке 1.
прямоугольной системе координат поверхность F задана уравнением F:
Решение: Приведем уравнение поверхности F к каноническому виду :
Следовательно, F – эллиптический цилиндр. Его направляющая y задается
уравнением y: (Она лежит в плоскости Oxz), а образующие параллельные
координатному вектору . Поверхность F изображена на рисунке 1.
Слайд 15 Определите вид цилиндрической поверхности F,
найдите уравнение её
направляющей y, направление образующих и изобразите эту поверхность, если в
прямоугольной системе координат поверхность F задана уравнением F:
Решение: Приведем уравнение поверхности F к каноническому виду :
Следовательно, F – гиперболический цилиндр. Его направляющая y задается
уравнением y: (Она лежит в плоскости Oxy). y – гипербола с мнимой осью Ox.
Поверхность F изображена на рисунке 2.
направляющей y, направление образующих и изобразите эту поверхность, если в
прямоугольной системе координат поверхность F задана уравнением F:
Решение: Приведем уравнение поверхности F к каноническому виду :
Следовательно, F – гиперболический цилиндр. Его направляющая y задается
уравнением y: (Она лежит в плоскости Oxy). y – гипербола с мнимой осью Ox.
Поверхность F изображена на рисунке 2.
Слайд 16 3. Найти точки пересечения поверхности
и прямой:
и
Решение: ,
Полученную систему подставим в исходное уравнение.
или отсюда .
и
Решение: ,
Полученную систему подставим в исходное уравнение.
или отсюда .