- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему построение сечений 2
Содержание
- 1. Презентация по математике на тему построение сечений 2
- 2. Существование плоскостиС1. Какова бы ни была плоскость
- 3. Основной закон!Через две точки плоскости можно провести прямую и только одну.
- 4. Построение сечения пирамидызадача: построить сечение ,проходящее через
- 5. ПОЛНОЕ ОПИСАНИЕ ПОСТРОЕНИЯ К СЛАЙДУ №31.Через три
- 6. Построение сечения тетраэдраПостроить сечение тетраэдра ABCD плоскостью
- 7. Построение сечений кубаABCDA1B1C1D1 - куб, Е –
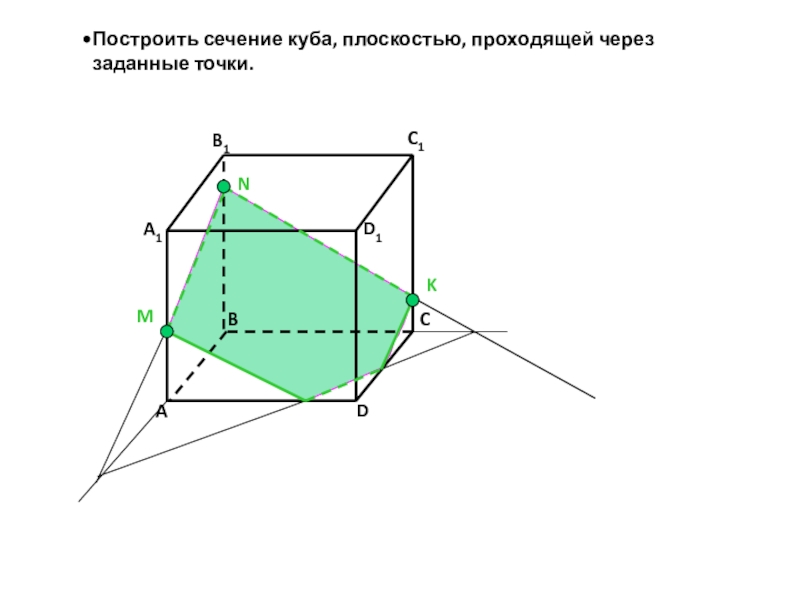
- 8. Построить сечение куба, плоскостью, проходящей через заданные точки.MNKABCDA1B1C1D1
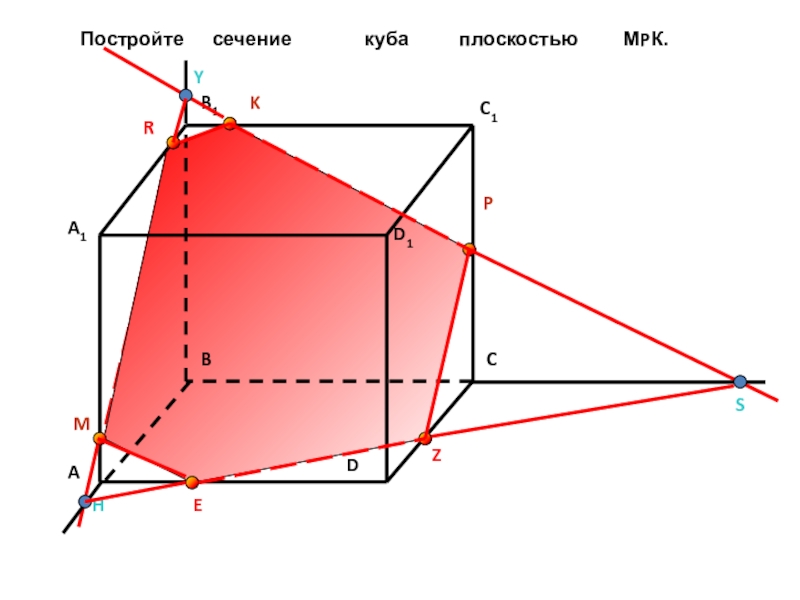
- 9. Постройте сечение
- 10. Надеюсь, что данная презентация помогла повторить основные правила построения сечений многогранников. Удачи!
Слайд 1Для самостоятельного изучения
Матлашевская Лилия Петровна
Учитель математики
МАОУ «Гимназия № 2» г.Перми
Слайд 2Существование плоскости
С1. Какова бы ни была плоскость , существуют точки, принадлежащие
С2.Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
С3.Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.
Т.15.1. Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну.
Т.15.3. Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.
Слайд 4Построение сечения пирамиды
задача: построить сечение ,проходящее через вершину D и точки
M
N
1.M↔N
2.M↔D
3.M↔N
4.Искомое сечение - ∆MDN.
B
Слайд 5ПОЛНОЕ ОПИСАНИЕ ПОСТРОЕНИЯ К СЛАЙДУ №3
1.Через три точки всегда можно провести
( обозначим её α) и притом только одну.
2.Так как точки М и Nявляются общими для плоскостей α и пл. АВС , то прямая MN является прямой пересечения этих плоскостей ( соединим точки M и N отрезком) ( по С2).
3. Подобными рассуждениями обосновывается возможность соединить точки М и D, и точки N иD .
4.Искомое сечение - ∆MDN.
Слайд 6Построение сечения тетраэдра
Построить сечение тетраэдра ABCD плоскостью ,проходящей через точки M,N,P,
В
М
N
Р
1.M↔N
2.N↔P
3.MN n AC ↔ Q
Q
4. PQ n AB ↔ S
S
5. S ↔M
6.четырёхугол.SMNP – искомое сечение
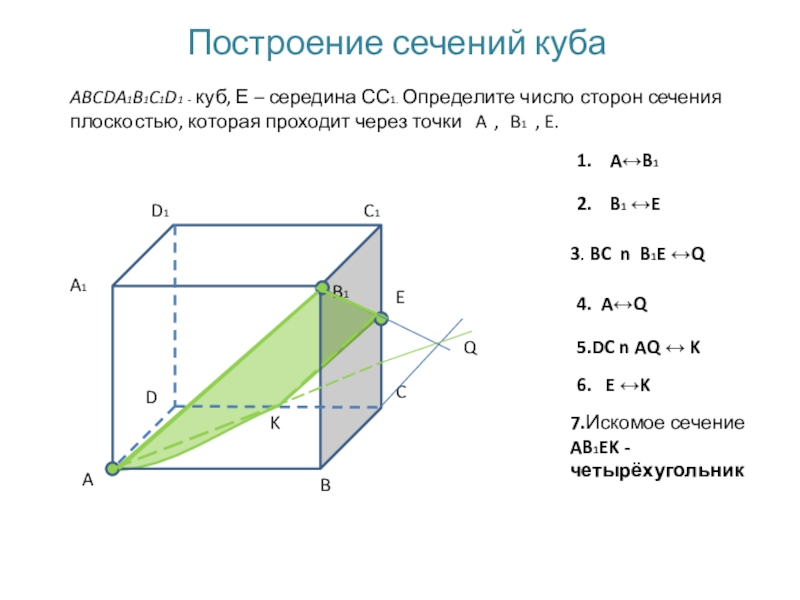
Слайд 7Построение сечений куба
ABCDA1B1C1D1 - куб, Е – середина СС1. Определите число
E
1. A↔B1
2. B1 ↔E
3. BC n B1E ↔Q
Q
4. A↔Q
5.DC n AQ ↔ K
K
6. E ↔K
7.Искомое сечение AB1EK - четырёхугольник
Слайд 10Надеюсь, что данная презентация помогла повторить основные правила построения сечений многогранников.
Удачи!