- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Построение сечения многогранников
Содержание
- 1. Презентация по математике на тему Построение сечения многогранников
- 2. Учебная задача:Основная задача состоит в построении сечения
- 3. Вспомогательные задачи из курса геометрии:1. Пересечение двух
- 4. Пересечение двух прямых Точка, в которой
- 5. Параллельное проектирование Если известны параллельные
- 6. Центральное проектирование Пересечение прямой АВ и плоскости
- 7. Пересечение двух плоскостейЛинию пересечения плоскостей АВС и
- 8. Сечение параллелепипеда плоскостью Построим
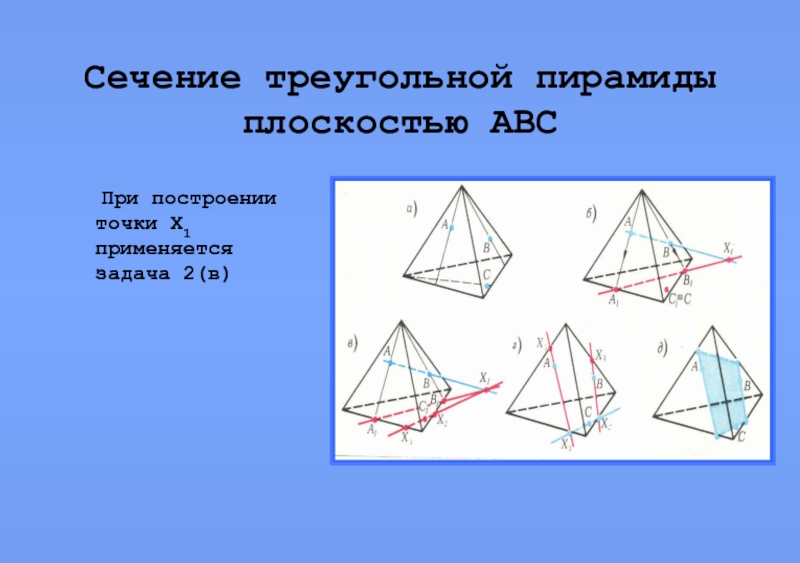
- 9. Сечение треугольной пирамиды плоскостью АВС При построении точки Х1 применяется задача 2(в)
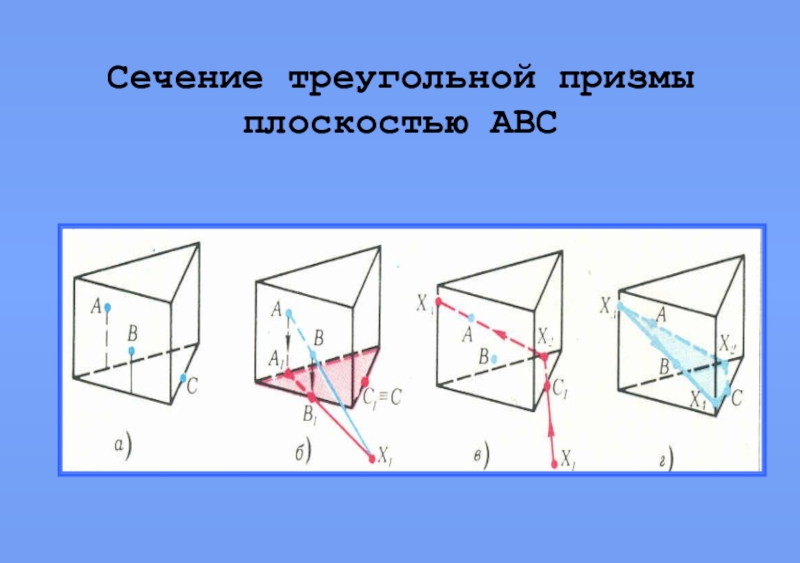
- 10. Сечение треугольной призмы плоскостью АВС
Учебная задача:Основная задача состоит в построении сечения многогранника плоскостью, то есть в построении пересечения этих двух множеств. Изображение многогранника будет считаться заданным, а плоскость сечения будет дана тремя точками. Задача считается решенной, если найдены все отрезки
Слайд 2Учебная задача:
Основная задача состоит в построении сечения многогранника плоскостью, то есть
в построении пересечения этих двух множеств. Изображение многогранника будет считаться заданным, а плоскость сечения будет дана тремя точками. Задача считается решенной, если найдены все отрезки по которым плоскость сечения пересекает грани многогранника. Пользоваться можно только линейкой и циркулем.
На чертежах синий цвет будет соответствовать секущей плоскости, а красный - той плоскости, в которой находится линия пересечения.
На чертежах синий цвет будет соответствовать секущей плоскости, а красный - той плоскости, в которой находится линия пересечения.
Слайд 3Вспомогательные задачи из курса геометрии:
1. Пересечение двух прямых
2. Пересечение прямой и
плоскости
а) параллельное проектирование
в) центральное проектирование
3. Пересечение двух плоскостей
а) параллельное проектирование
в) центральное проектирование
3. Пересечение двух плоскостей
Слайд 4Пересечение двух прямых
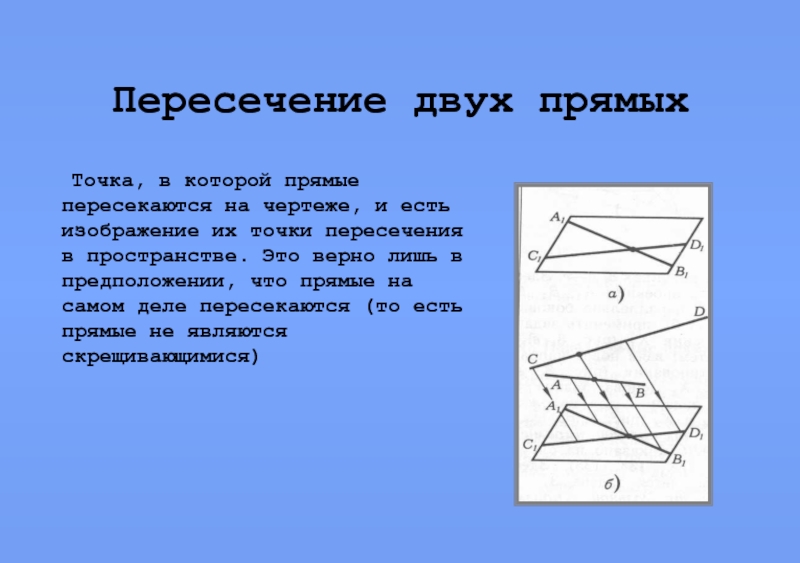
Точка, в которой прямые пересекаются на чертеже,
и есть изображение их точки пересечения в пространстве. Это верно лишь в предположении, что прямые на самом деле пересекаются (то есть прямые не являются скрещивающимися)
Слайд 5Параллельное проектирование
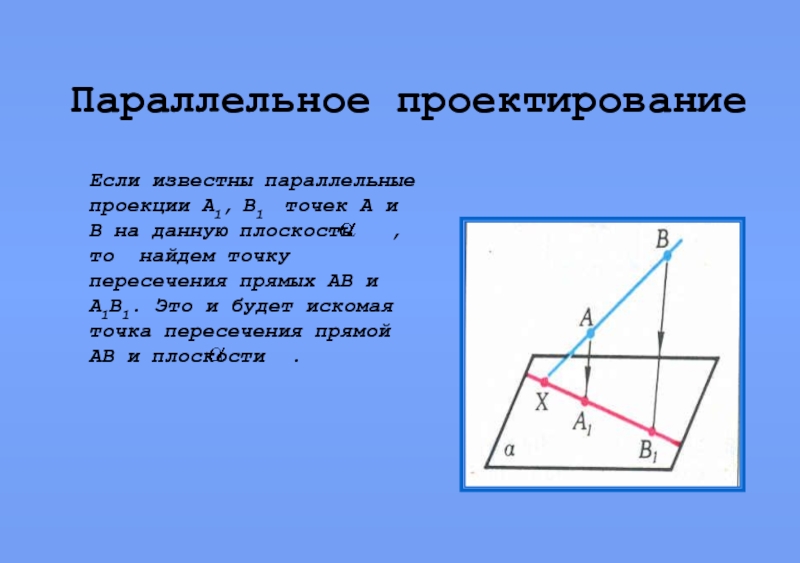
Если известны параллельные проекции А1, В1 точек
А и В на данную плоскость , то найдем точку пересечения прямых АВ и А1В1. Это и будет искомая точка пересечения прямой АВ и плоскости .
Слайд 6Центральное проектирование
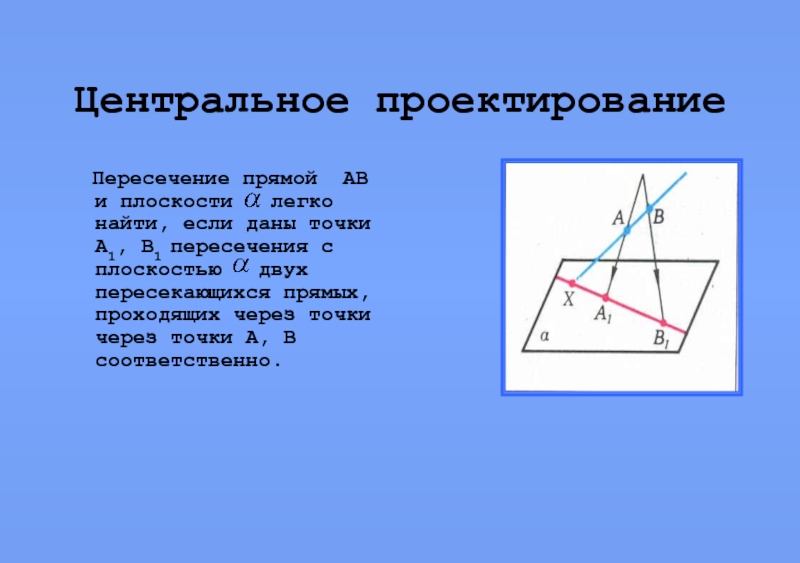
Пересечение прямой АВ и плоскости легко найти, если
даны точки А1, В1 пересечения с плоскостью двух пересекающихся прямых, проходящих через точки через точки А, В соответственно.
Слайд 7Пересечение двух плоскостей
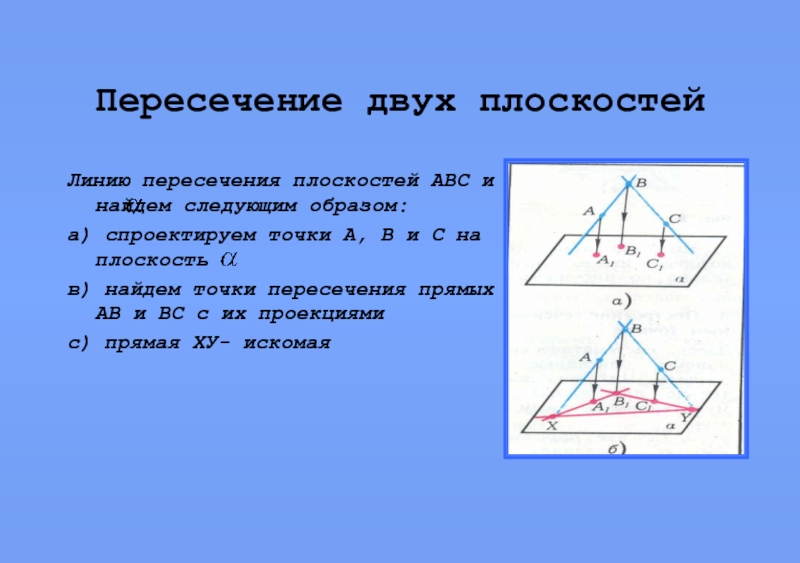
Линию пересечения плоскостей АВС и найдем следующим образом:
а)
спроектируем точки А, В и С на плоскость
в) найдем точки пересечения прямых АВ и ВС с их проекциями
с) прямая ХУ- искомая
в) найдем точки пересечения прямых АВ и ВС с их проекциями
с) прямая ХУ- искомая
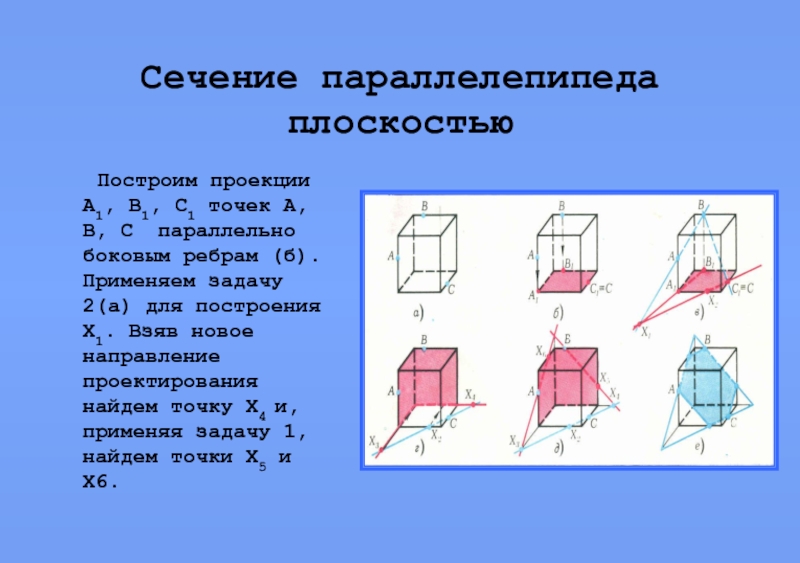
Слайд 8Сечение параллелепипеда плоскостью
Построим проекции А1, В1, С1
точек А, В, С параллельно боковым ребрам (б). Применяем задачу 2(а) для построения Х1. Взяв новое направление проектирования найдем точку Х4 и, применяя задачу 1, найдем точки Х5 и Х6.