- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Понятие векторов. Равенство векторов
Содержание
- 1. Презентация по математике на тему Понятие векторов. Равенство векторов
- 2. Многие физические величины, например
- 3. При изучении электрических и магнитных явлений появляются новые примеры векторных величин.
- 4. Электрический ток, т.е. направленное
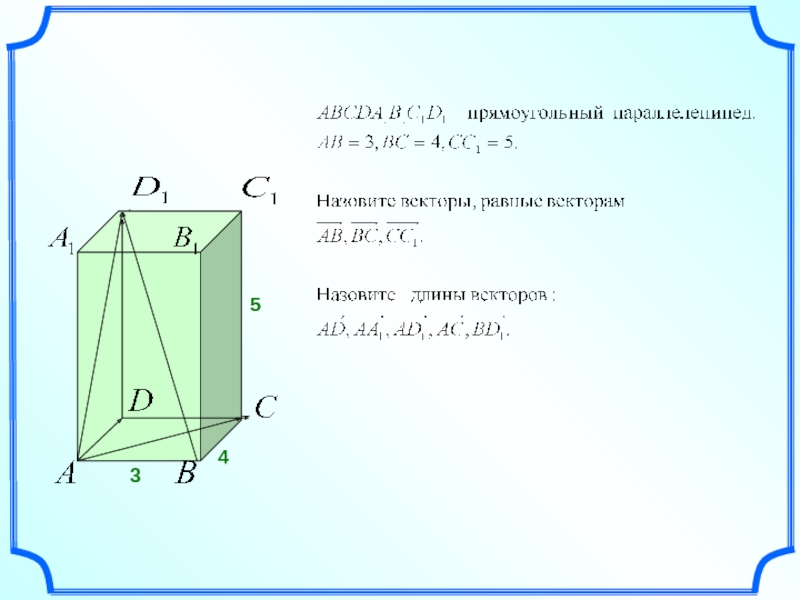
- 5. САВD45M В прямоугольнике АВСD АВ=3см,
- 6. АВСD – прямоугольная трапеция.Найти ABCD125450Решение5577
- 7. Длиной или модулем вектора называется длина отрезка
- 8. Любая точка плоскости также
- 9. Два ненулевых вектора называются коллинеарными,
- 10. Два ненулевых вектора называются коллинеарными,
- 11. Векторы называются равными,
- 12. Слайд 12
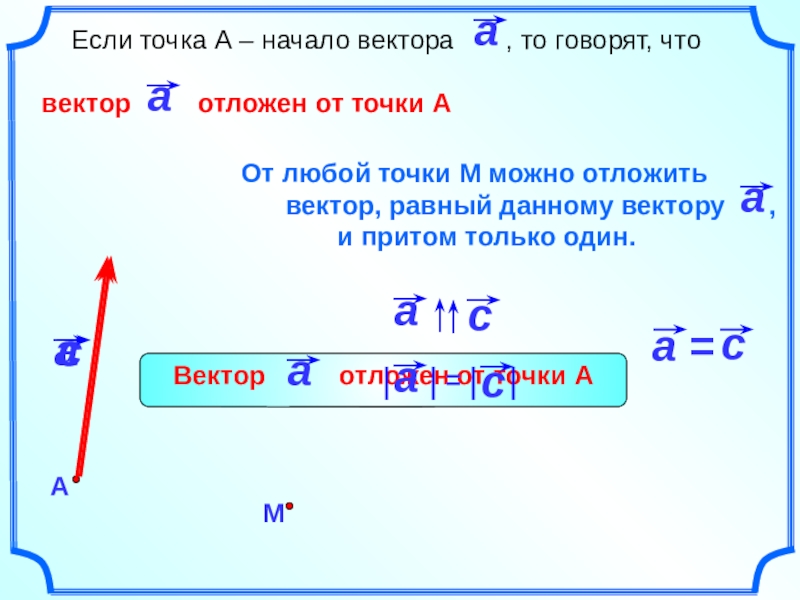
- 13. Если точка А –
- 14. И. п. - сидя на стуле. 1-2
- 15. АВNCKDMДано: ABCD – тетраэдр. Точки M, N,
- 16. А1В1МС1КАВСD1DДан параллелепипед ABCDA1B1C1D1. Точки M и K
- 17. Самостоятельная работа АВСА1В1С1D1DДано: ABCDA1B1C1D1 – прямоугольный параллелепипед,
- 18. Итог урока
Многие физические величины, например сила, перемещение материальной точки, скорость, характеризуются не только своим числовым значением, но и направлением в пространстве. Такие физические величины называются векторными величинами (или коротко векторами)8 Н
Слайд 2
Многие физические величины, например
сила, перемещение материальной
точки, скорость, характеризуются не только своим числовым значением, но и направлением в пространстве. Такие физические величины называются векторными величинами (или коротко векторами)
8 Н
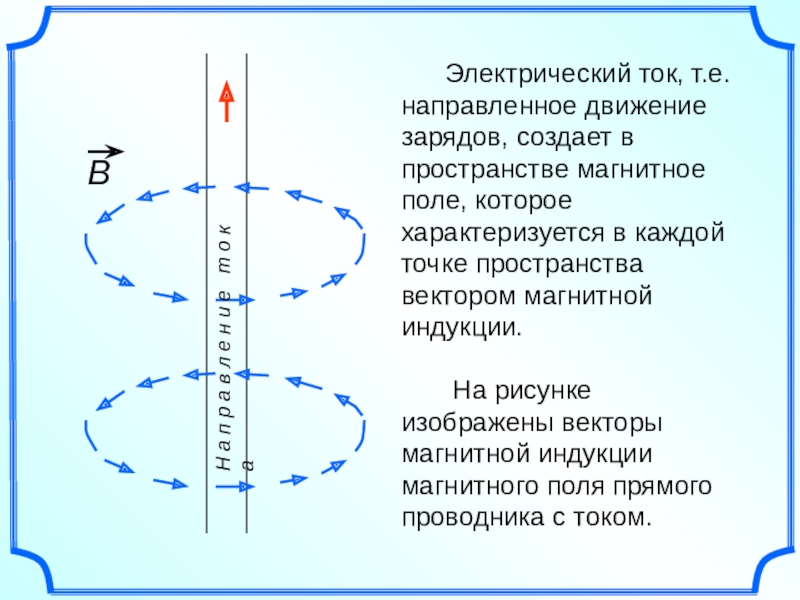
Слайд 4 Электрический ток, т.е. направленное движение зарядов, создает в
пространстве магнитное поле, которое характеризуется в каждой точке пространства вектором магнитной индукции.
На рисунке изображены векторы магнитной индукции магнитного поля прямого проводника с током.
На рисунке изображены векторы магнитной индукции магнитного поля прямого проводника с током.
Слайд 5
С
А
В
D
4
5
M
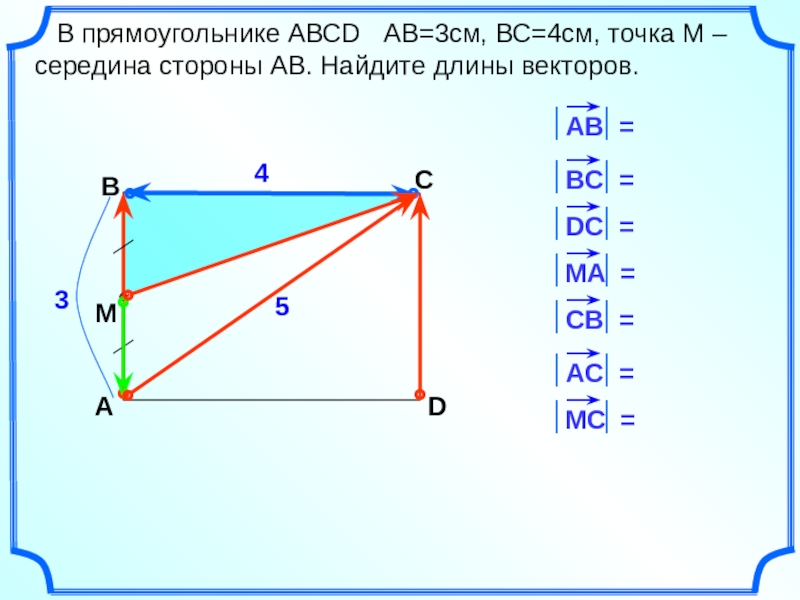
В прямоугольнике АВСD АВ=3см, ВС=4см, точка М –
середина стороны АВ. Найдите длины векторов.
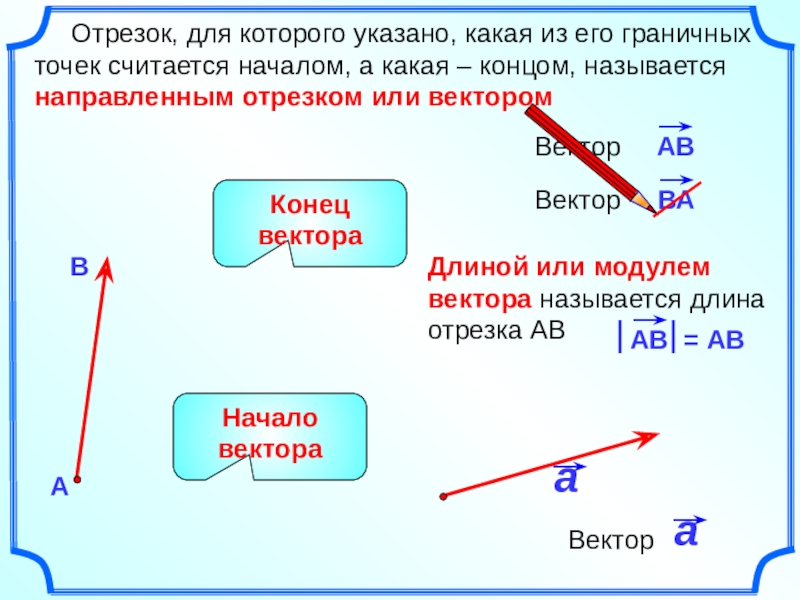
Слайд 7Длиной или модулем вектора называется длина отрезка АВ
Отрезок,
для которого указано, какая из его граничных точек считается началом, а какая – концом, называется направленным отрезком или вектором
Начало вектора
Конец вектора
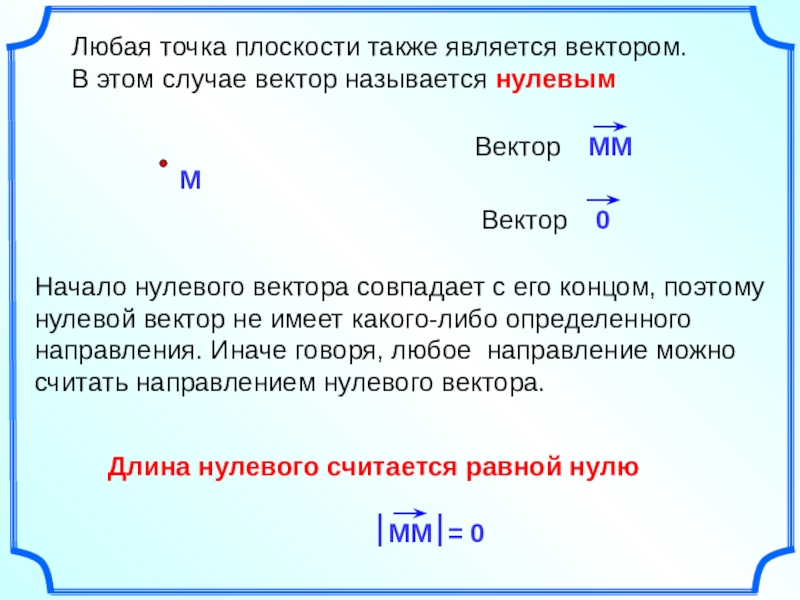
Слайд 8 Любая точка плоскости также является вектором.
В этом случае вектор называется нулевым
Длина нулевого считается равной нулю
Начало нулевого вектора совпадает с его концом, поэтому нулевой вектор не имеет какого-либо определенного направления. Иначе говоря, любое направление можно считать направлением нулевого вектора.
Слайд 9
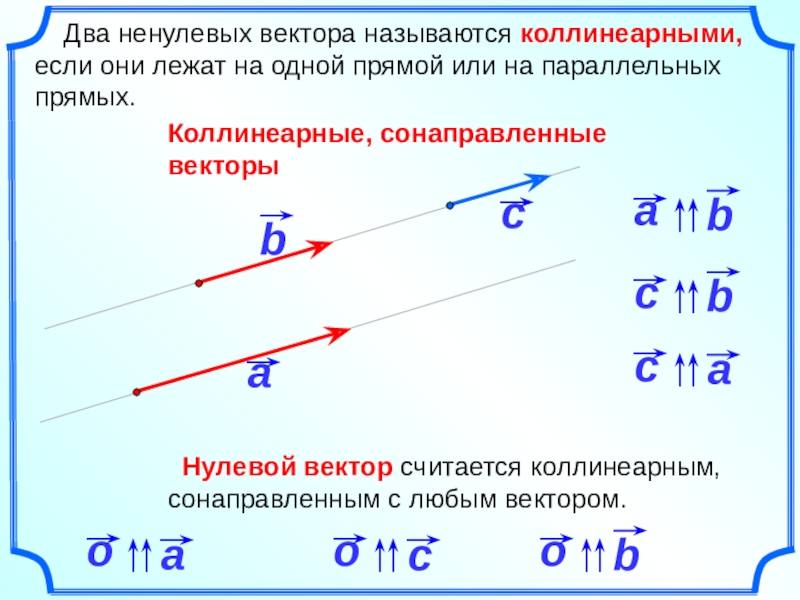
Два ненулевых вектора называются коллинеарными, если они лежат на
одной прямой или на параллельных прямых.
Коллинеарные, сонаправленные векторы
Нулевой вектор считается коллинеарным, сонаправленным с любым вектором.
Слайд 10
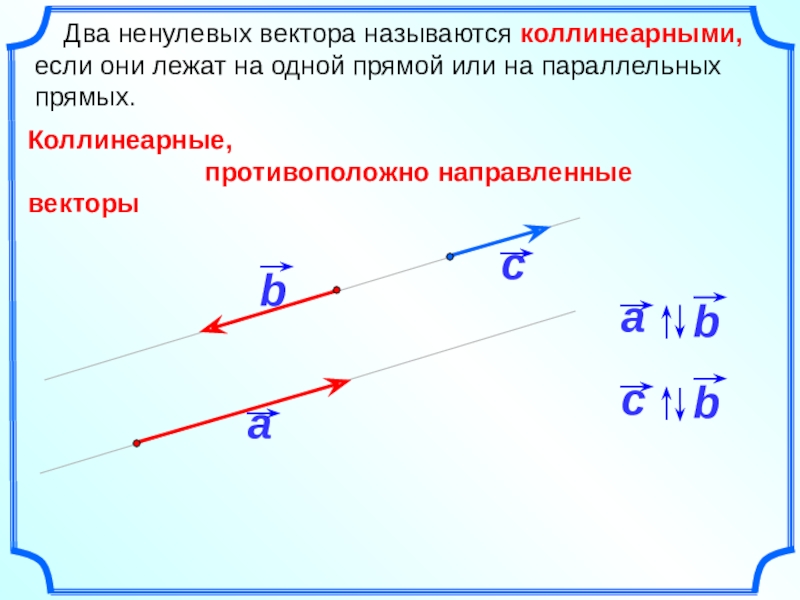
Два ненулевых вектора называются коллинеарными, если они лежат на
одной прямой или на параллельных прямых.
Коллинеарные,
противоположно направленные векторы
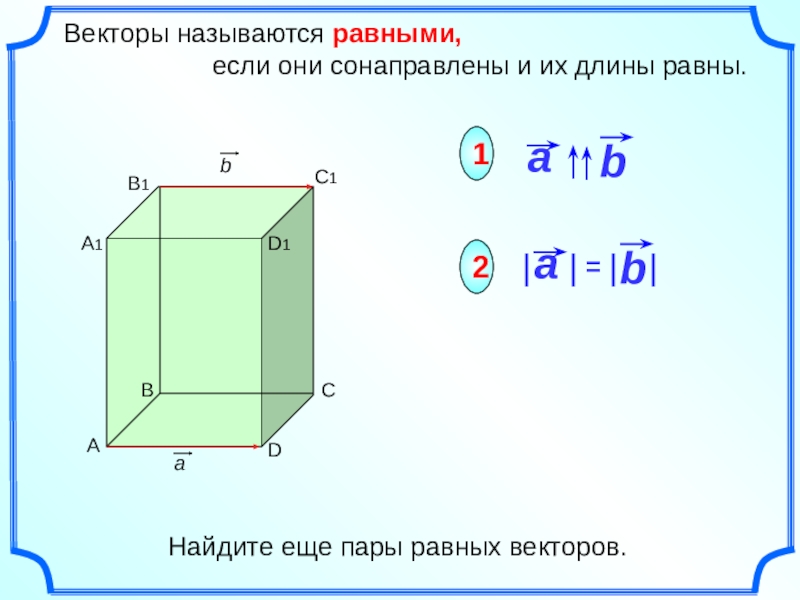
Слайд 11 Векторы называются равными,
если они сонаправлены и их длины равны.
1
2
Найдите еще пары равных векторов.
А
В
С
D
А1
B1
C1
D1
a
b
Слайд 14И. п. - сидя на стуле.
1-2 – отвести голову назад
и плавно наклонить назад,
3-4 - голову наклонить вперед, плечи не поднимать.
Повторить 4—6 раз. Темп медленный.
2. Быстро поморгать, закрыть глаза и посидеть спокойно, медленно считая до 5.
Повторить 4-5 раз.
3. Крепко зажмурить глаза (считать до 3),
открыть их и посмотреть вдаль (считать до 5).
Повторить 4-5 раз.
3-4 - голову наклонить вперед, плечи не поднимать.
Повторить 4—6 раз. Темп медленный.
2. Быстро поморгать, закрыть глаза и посидеть спокойно, медленно считая до 5.
Повторить 4-5 раз.
3. Крепко зажмурить глаза (считать до 3),
открыть их и посмотреть вдаль (считать до 5).
Повторить 4-5 раз.
Физкультминутка
Слайд 15А
В
N
C
K
D
M
Дано: ABCD – тетраэдр. Точки M, N, K – середины AC,
BC, CD; соответственно, AB=3 см, BC=4 см, BD=5 см.
Найти: AB, BC, BD, NM, BN, NK.
Найти: AB, BC, BD, NM, BN, NK.
№ 320 (а)
Слайд 16
А1
В1
М
С1
К
А
В
С
D1
D
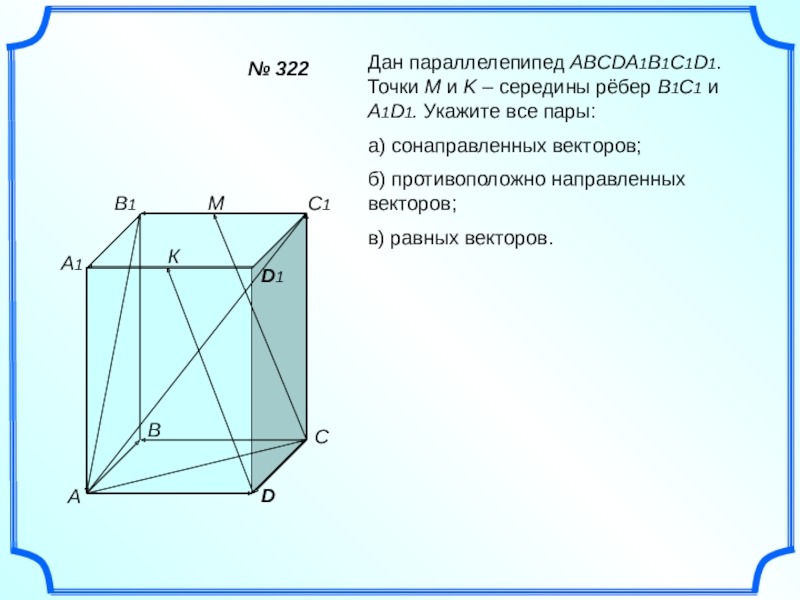
Дан параллелепипед ABCDA1B1C1D1. Точки M и K – середины рёбер B1C1
и A1D1. Укажите все пары:
а) сонаправленных векторов;
б) противоположно направленных векторов;
в) равных векторов.
а) сонаправленных векторов;
б) противоположно направленных векторов;
в) равных векторов.
№ 322
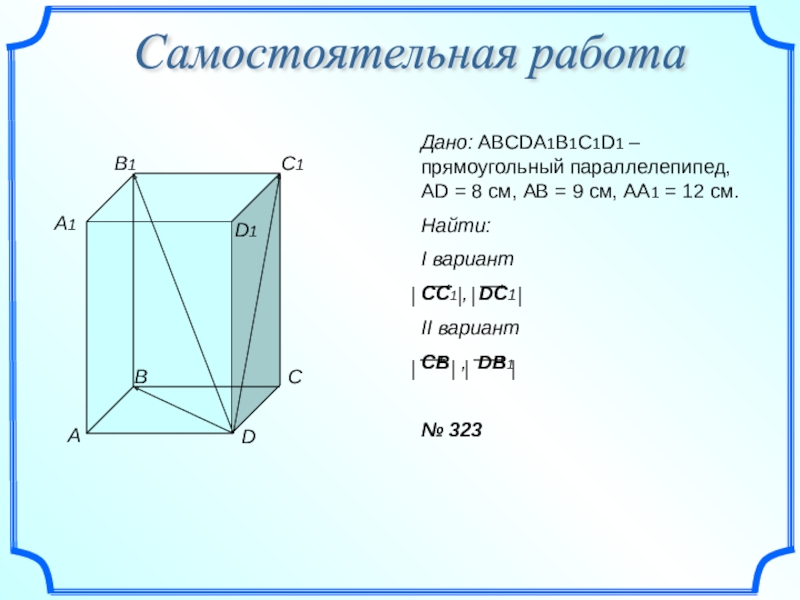
Слайд 17Самостоятельная работа
А
В
С
А1
В1
С1
D1
D
Дано: ABCDA1B1C1D1 – прямоугольный параллелепипед, AD = 8 см,
AB = 9 см, AA1 = 12 см.
Найти:
I вариант
CC1 , DC1
II вариант
CB , DB1
№ 323
Найти:
I вариант
CC1 , DC1
II вариант
CB , DB1
№ 323
