Руководитель: Захарова Галина Михайловна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему: Пирамида-гениальная находка природы
Содержание
- 1. Презентация по математике на тему: Пирамида-гениальная находка природы
- 2. Введение Программа дисциплины «математика» в
- 3. Пирамиды и математика
- 4. Очень часто в своих
- 5. Слайд 5
- 6. Ещё несколько примеров о магических свойствах пирамид
- 7. В 1977 году близ города Осташкова на
- 8. Данная информация, полученная из различных источников, побудила меня к проведению нескольких экспериментов.
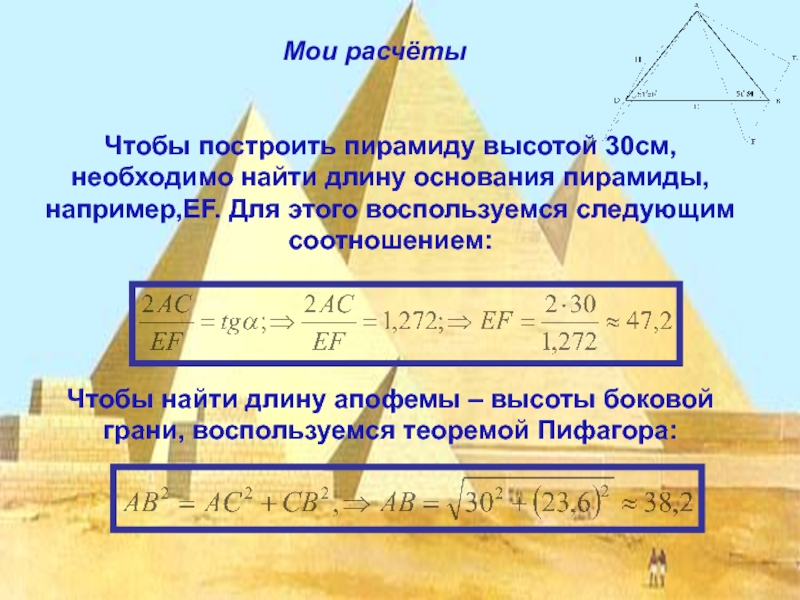
- 9. Мои расчётыЧтобы построить пирамиду высотой 30см,необходимо найти
- 10. 2-ой опыт: Сделав из картона пирамиду приблизительно
- 11. Вывод: пирамида – действительно, гениальная находка природы,
- 12. В большом энциклопедическом словаре пирамида определяется как
- 13. Почти пять тысячелетий тому
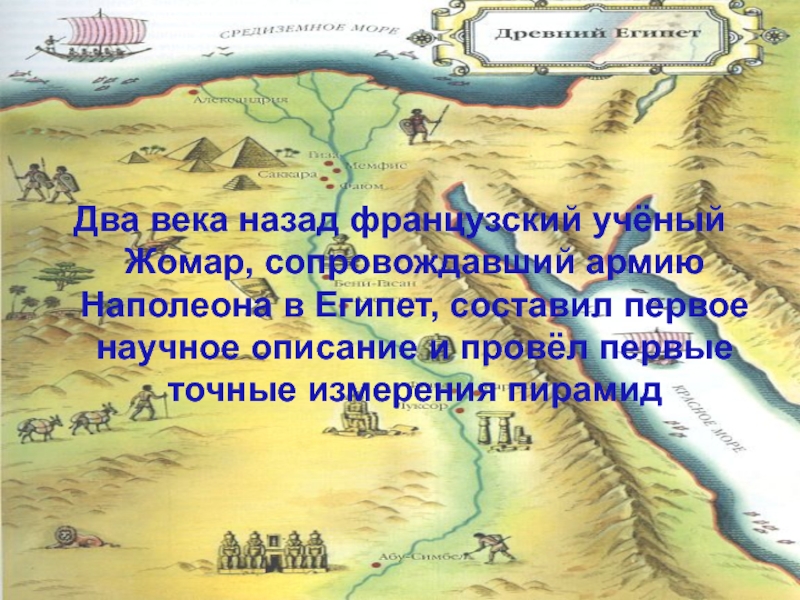
- 14. Два века назад французский учёный Жомар, сопровождавший
- 15. Три знаменитые большие пирамиды близ Гизы:
- 16. Самая высокая из них – пирамида Хеопса,
- 17. Из источников
- 18. * Изучая материал
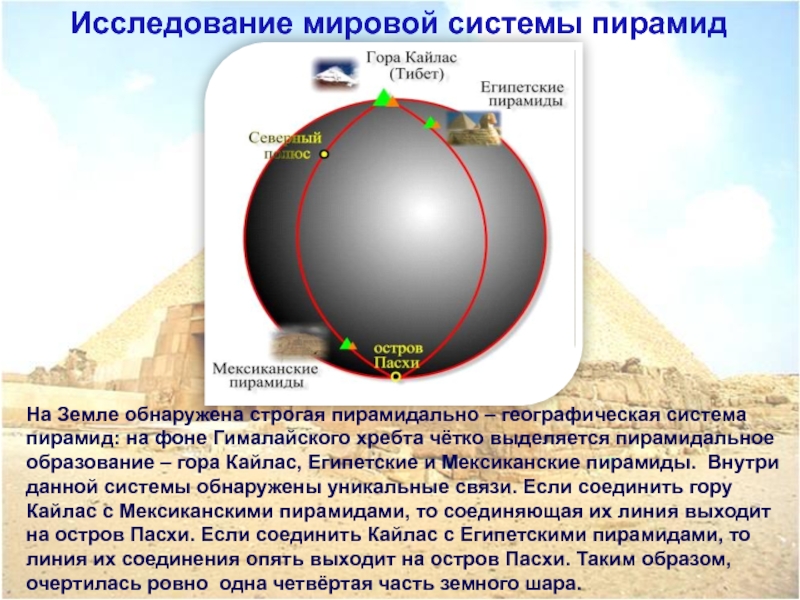
- 19. Исследование мировой системы пирамидНа Земле обнаружена строгая
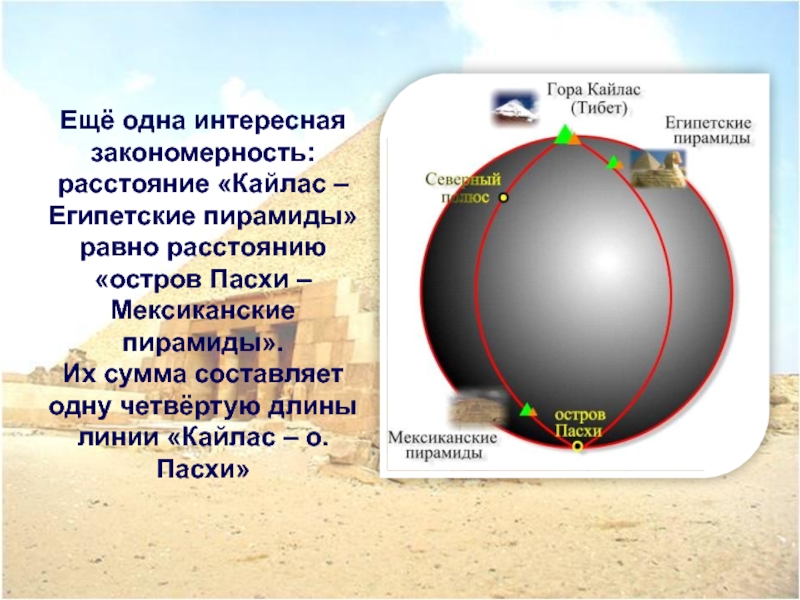
- 20. Ещё одна интересная закономерность: расстояние «Кайлас –
- 21. Пирамиды представляют большой интерес с точки зрения
- 22. Яркими представителями в этой области являются:Торговый
- 23. Тайницкая Благовещенская ПетровскаяКремлёвские башни
- 24. Троицкая Константино-Еленинская
- 25. В заключение представляю свои исследования в области
- 26. Начав своё исследование по выявлению пирамид в
- 27. Ворота и ограждения некоторых жилых домов
- 28. Дворец, да и только! Жилой дом по улице Фурманова
- 29. Величавый и могучий «Илья Муромец» по ул. Социалистической
- 30. Сказочно смотрятся беседки на игровых площадках детских садов
- 31. Пирамидами привлекает внимание сооружение
- 32. Выбранная с помощью руководителя тема для исследования,
- 33. 1. А.М. Прохоров и др. «Математический энциклопедический
Слайд 2Введение
Программа дисциплины «математика» в разделе «Поверхности
и
темы: «Пирамида и её свойства». Это наиболее интересный
материал данного раздела, потому что пирамида, как
геометрическая форма, пожалуй, одно из самых совершенных в
природе тел. Материя, пытаясь сохранить самоё себя в вечной борьбе со временем, ищет самые безопасные, устойчивые, энергетически комфортные формы.
«Это горы камня, возведённые на горах камня»,-сказал греческий философ.
«Всё боится времени, а время боится пирамид»,-провозгласили арабы.
«Стоя перед пирамидами, вы плотно запахиваете пальто, потому что вас бьёт дрожь, и вы не можете вымолвить ни слова»,-написал Гюстав Флобер.
«Солдаты! На вас смотрят сорок веков»,-воскликнул Наполеон перед знаменитой битвой с мамлюками на плато Гиза.
В связи с этим встаёт вопрос: в чём тайна пирамид? В чём сила их притягательности? Чтобы ответить на данные вопросы, я буду рассматривать пирамиду с различных точек зрения.
Цель исследования: на конкретных и доступных примерах доказать, что пирамида – уникальная и гениальная находка природы, обладающая магическими свойствами; показать историческую сущность и географическую значимость; убедить в том, что её геометрическая форма самая совершенная и красивая.
Слайд 3Пирамиды и математика
Кроме того, с математической точки зрения пирамиду характеризует следующие параметры : боковые рёбра, стороны основания, высота – перпендикуляр, опущенный из вершины на плоскость основания, апофема – высота боковой грани.
Площадь боковой поверхности вычисляется по формуле:
Объём пирамиды вычисляется по формуле:
Слайд 4 Очень часто в своих исследованиях учёные используют свойства
Проведем анализ размеров пирамиды Хеопса, следуя рассуждениям, приведенным в замечательной книге украинского ученого Николая Васютинского "Золотая пропорция" (1990 г.).
В 1837 г. английский полковник Г. Вайз измерил угол наклона граней пирамиды: он оказался равным a = 51°51'. Эта величина и сегодня признается большинством исследователей. Указанному значению угла отвечает tg a = 1,27306. Эта величина соответствует отношению высоты пирамиды Н к половине ее основания с, то есть H / (с / 2) = 2H / с.
И вот здесь исследователей ожидал большой сюрприз! Дело в том, что если взять корень квадратный из золотой пропорции √t , то мы получим следующий результат √t = 1,272. Сравнивая эту величину с величиной tg a = 1,27306, мы видим, что эти величины очень близки между собой. Если же принять угол a = 51°50', то есть уменьшить его всего на одну угловую минуту, то величина tg a станет равной 1,272, совпадающей с величиной √t. Следует отметить, что в 1840 г. Г. Вайз повторил свои измерения и уточнил, что значение угла a =51°50'.
Слайд 5
Пирамида с пропорциями Золотого
Многие учёные исследовали уникальные свойства пирамиды с пропорциями Золотого сечения и были очень удивлены тем, что при морозе 40º внутри пирамиды не замерзает обычная вода, но при встряхивании бутылки она замерзает за 2-3 секунды.
Эксперименты проводились и в области сельского хозяйства. В Днепропетровской и Запорожской областях были засеяны тысячи гектаров семенами различных культур, побывавшими в пирамиде с пропорциями Золотого сечения. Прибавка урожая составила от 30% до 50%. Даже в условиях засухи растения прекрасно росли и развивались.
Слайд 6Ещё несколько примеров о магических свойствах пирамид
Вернувшись во Францию, он построил деревянную модель пирамиды с длиной основания около одного метра. Сориентировав её по сторонам света и поместив туда тело мёртвой кошки, он через несколько дней обнаружил её мумифицировавшейся.
Того же эффекта он достигал и с другими органическими веществами, которые в дальнейшем не портились и не гнили.
Слайд 7В 1977 году близ города Осташкова на берегу озера Селигер была
Детский писатель Владислав Крапивин в одной из своих повестей рассказывает о магической силе пирамид, описывая, как пятиклассник обыгрывает директора школы в шахматы, одевая во время игры на голову бумажную шляпу в форме пирамиды.
Слайд 8Данная информация, полученная из различных источников, побудила меня к проведению нескольких
Слайд 9Мои расчёты
Чтобы построить пирамиду высотой 30см,необходимо найти длину основания пирамиды, например,EF.
Чтобы найти длину апофемы – высоты боковой грани, воспользуемся теоремой Пифагора:
Слайд 102-ой опыт: Сделав из картона пирамиду приблизительно с пропорциями Золотого сечения
3-ий опыт: Под ту же самую пирамиду поместила замоченные семена гороха. Другую порцию замочила в банке и поставила в другой комнате. Через три дня обнаружила, что горох пророс в обеих случаях, но его ростки под пирамидой были более крупными и имели зелёный окрас. Ростки гороха в банке были меньше и белые. Пророщенные семена посадили в один горшок. Семена, находившиеся под пирамидой взошли быстрее и через три дня я заметила, что всходы были низкорослые с многочисленными побегами, а всходы другого гороха были высокими и без побегов (только верхушка).
Слайд 11
Вывод: пирамида – действительно, гениальная находка природы, в которой пространство свернулось
Слайд 12
В большом энциклопедическом словаре пирамида определяется как монументальное сооружение, имеющее геометрическую
2-го тысячелетий до н. э., а так же постаменты храмов в Центральной и Южной Америке, связанные с космологическими культами.
История египетских пирамид
Слайд 13
Почти пять тысячелетий тому назад египетский фараон
Изучением пирамид занимались многие археологи, учёные, математики и все открывали их интересные свойства.
Слайд 14Два века назад французский учёный Жомар, сопровождавший армию Наполеона в Египет,
Слайд 15 Три знаменитые большие пирамиды близ Гизы: пирамиды фараона Хеопса, его
Слайд 16Самая высокая из них – пирамида Хеопса, или Большая пирамида, которая
В древности её высота достигала 148 метров. Сторона квадратного основания равна 233 метрам, а площадь основания превышает 54000 кв.м. Общий объём всего сооружения – более 2 500 000 куб.м. Сложена пирамида из 2 300 000 каменных глыб весом свыше 2-х тонн каждая. Глыбы со всех сторон гладко отшлифованы. Это значит, что строителям пришлось обработать около
14 000 000 поверхностей, т.к. каждый монолит имел 6 граней. И все поверхности отшлифованы с такой математической точностью, что между их соединениями нельзя просунуть лезвие ножа.
До 50-х годов 20-го столетия вес пирамиды превышал тоннаж всего военно-морского флота США, а её каменных блоков вполне хватило бы, чтобы построить город со стотысячным населением или обнести всю Францию стеной 3-х метровой высоты.
Геродот утверждал, что сооружение пирамиды длилось 20 лет и над ним работало в течение каждых трёх месяцев 100 тысяч человек.
Учёные утверждают, что творение Хеопса не могла бы уничтожить даже атомная бомба, сброшенная на Херосиму.
Слайд 17
Из источников научно – познавательной литературы
При их постройке было установлено, что квадрат, построенный на высоте пирамиды, в точности равен площади каждого из боковых треугольников. Это подтверждается и новейшими измерениями.
Мы знаем, что отношение между длинной окружности и ее диаметром, есть постоянная величина, хорошо известна не только математикам, но и школьникам – это число
=3,1416…
Если сложить 4 стороны основания пирамиды Хеопса, мы получим 931,22 м. Разделив это число на удвоенную высоту пирамиды (2·148,208),получим 3,1416…, то есть число
Следовательно, пирамида Хеопса – единственный в своём роде памятник, который представляет собой материальное воплощение числа , играющего важную роль в математике.
Слайд 18*
Изучая материал в различных источниках, я
Китай (долина пирамид), Россия (Алтайские пирамиды),
Северная Америка (подводные пирамиды на озере Рок),
Украина (крымские пирамиды), Франция (в Бретани) и, наконец, самый значительный комплекс пирамид в Тибете во главе с самой высокой из них — горой-пирамидой Кайлас.
Однако в расположении пирамид явно просматривается некоторая закономерность.
География пирамид
Слайд 19Исследование мировой системы пирамид
На Земле обнаружена строгая пирамидально – географическая система
Слайд 20Ещё одна интересная закономерность: расстояние «Кайлас – Египетские пирамиды»равно расстоянию «остров
Их сумма составляет одну четвёртую длины линии «Кайлас – о.Пасхи»
Слайд 21
Пирамиды представляют большой интерес с точки зрения архитектуры и дизайнерского искусства.
В наше время это очень модно и придаёт зданиям и другим сооружениям определённый шик.
Пирамиды в архитектуре
Слайд 22 Яркими представителями в этой области являются:
Торговый центр в Илинге, Лондон
Стеклянная
Слайд 25В заключение представляю свои исследования в области архитектуры и дизайнерского искусства
Свой родной город я не могу и не буду сравнивать ни с Лондоном, ни с Парижем, ни с Москвой, но с уверенностью хочу заявить, что он преображается и хорошеет с каждым днём. А пирамиды, используемые в архитектуре придают ему интересный и загадочный вид.
Слайд 26Начав своё исследование по выявлению пирамид в архитектуре своего города, я
Слайд 32Выбранная с помощью руководителя тема для исследования, была очень интересной и
Изученный материал, результаты моих экспериментов позволяют сделать вывод, что цель моего исследования достигнута.
Заключение
Слайд 331. А.М. Прохоров и др. «Математический энциклопедический словарь».- М.:Советская энциклопедия, 1988.
2.
3. Терра – Лексикон: «Иллюстрированный энциклопедический словарь».-М.: ТЕРРА,1998.
4. Всемирная история (энциклопедия для детей). – М.: «Аванта+»,1993.
5. В Уваров «Волшебные свойства пирамид». Лениздат; 2006.
6. Г. Райхардт «Семь чудес света», 1996.
7. В.П. Бабанин «Тайны великих пирамид».
С-Пб.; Лань, 1999.
8. Интернет – ресурсы.
Список используемой литературы