Т. А.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Параллельное проектирование. Площадь ортогональной проекции. Изображение пространственных фигур.
Содержание
- 1. Презентация по математике на тему Параллельное проектирование. Площадь ортогональной проекции. Изображение пространственных фигур.
- 2. Цели урокаобучающая: сформулировать понятие параллельного проектирования; формировать
- 3. Параллельное проектированиеПусть π - некоторая плоскость, l
- 4. Свойство №1Если прямая параллельна или совпадает с
- 5. Свойство №2Параллельное проектирование сохраняет отношение длин отрезков,
- 6. Свойство №3Если две параллельные прямые не параллельны
- 7. Ортогональная проекция точкиОртогональной проекцией точки А на
- 8. Ортогональная проекция фигурыОртогональной проекцией фигуры на данную
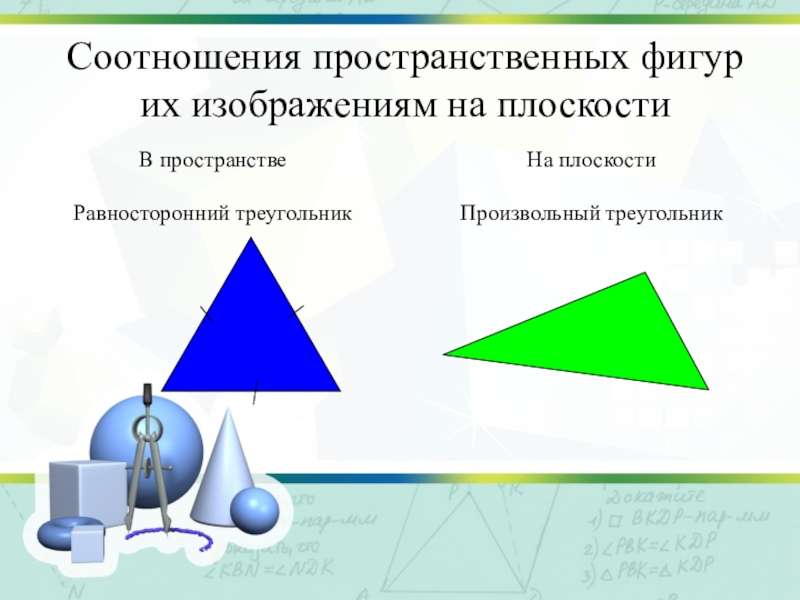
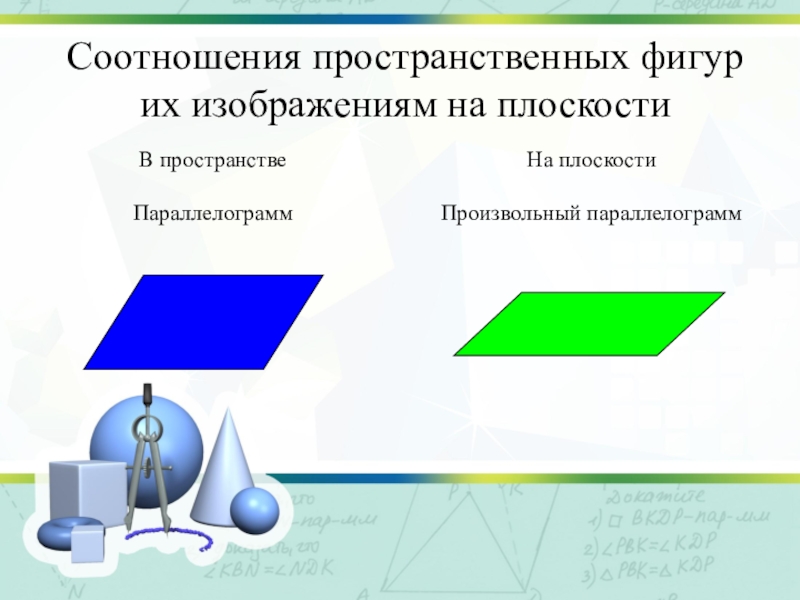
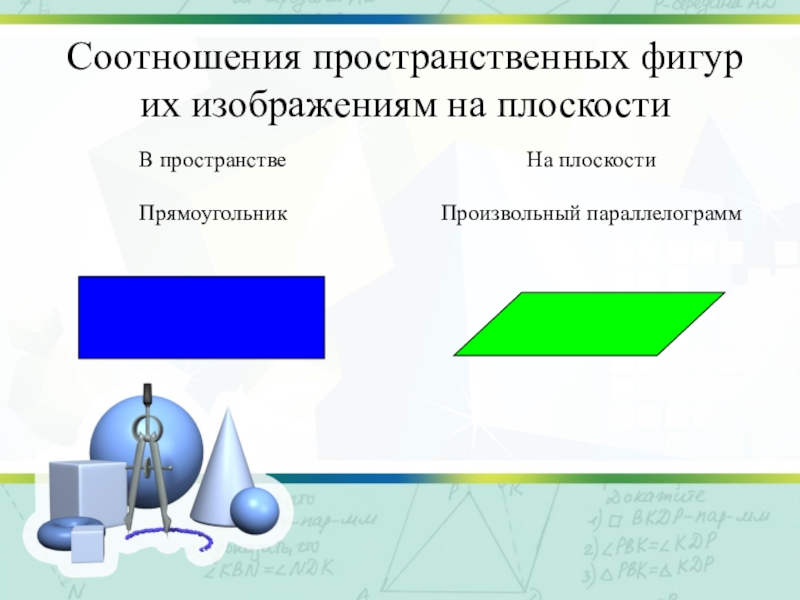
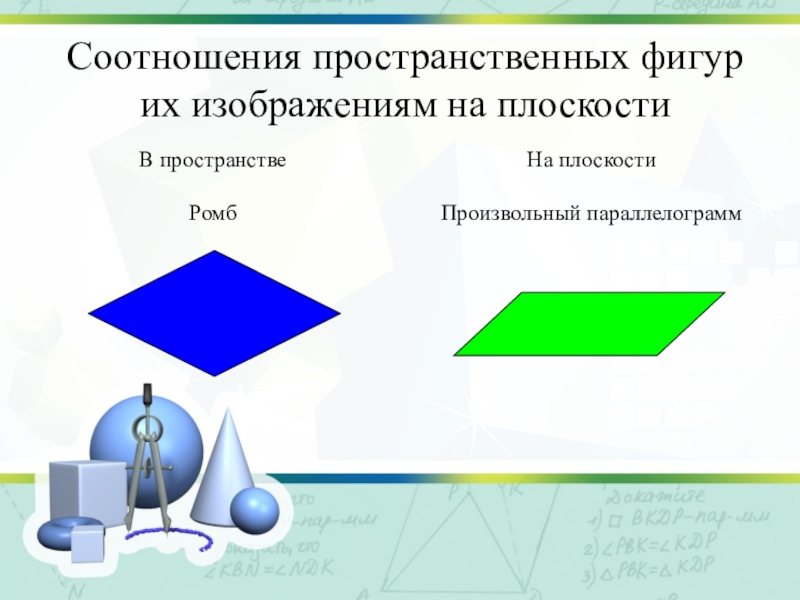
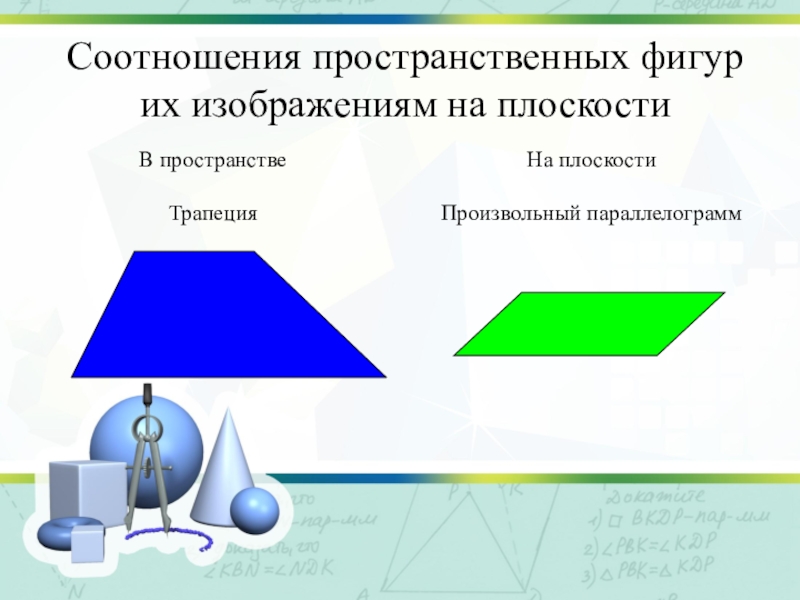
- 9. Соотношения пространственных фигур их изображениям на плоскости
- 10. Соотношения пространственных фигур их изображениям на плоскости
- 11. Соотношения пространственных фигур их изображениям на плоскости
- 12. Соотношения пространственных фигур их изображениям на плоскости
- 13. Соотношения пространственных фигур их изображениям на плоскости
- 14. Соотношения пространственных фигур их изображениям на плоскости
- 15. Алгоритм построения изображения пирамидыИзображение пирамиды всегда начинают
- 16. Алгоритм изображения призмыИзображение призмы всегда начинают с
- 17. Домашнее задание Записать опорный конспект согласно материалу
Цели урокаобучающая: сформулировать понятие параллельного проектирования; формировать у учащихся умение применять понятия и свойства параллельного проектирования к решению задач; развивающая: развивать абстрактное мышление, пространственное воображение и интуицию;воспитательная: содействовать формированию и развитию ответственности, познавательного интереса к изучаемой
Слайд 1Тема: Параллельное проектирование. Площадь ортогональной проекции.
Изображение пространственных фигур.
Преподаватель ГБПОУ КСУ №32
Малькова
Слайд 2Цели урока
обучающая: сформулировать понятие параллельного проектирования; формировать у учащихся умение применять
понятия и свойства параллельного проектирования к решению задач;
развивающая: развивать абстрактное мышление, пространственное воображение и интуицию;
воспитательная: содействовать формированию и развитию ответственности, познавательного интереса к изучаемой дисциплине.
развивающая: развивать абстрактное мышление, пространственное воображение и интуицию;
воспитательная: содействовать формированию и развитию ответственности, познавательного интереса к изучаемой дисциплине.
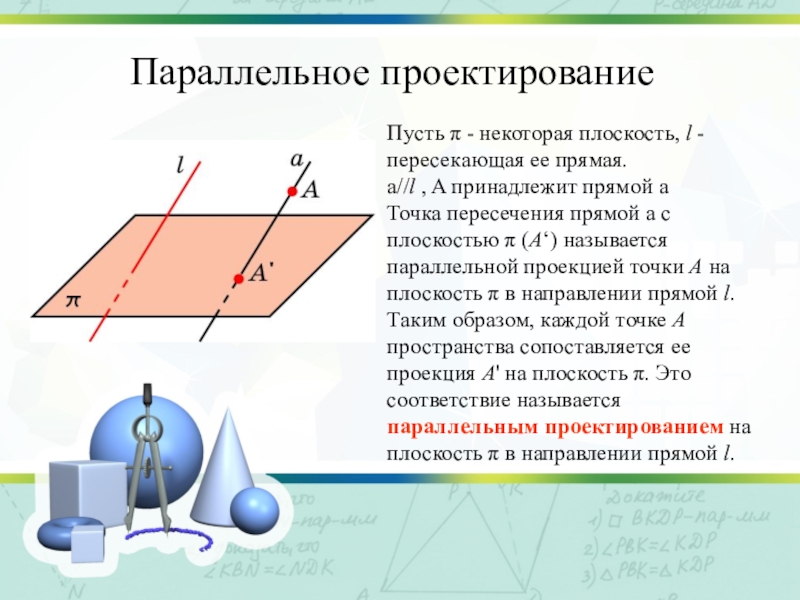
Слайд 3Параллельное проектирование
Пусть π - некоторая плоскость, l - пересекающая ее прямая.
a//l , A принадлежит прямой a
Точка пересечения прямой a с плоскостью π (A‘) называется параллельной проекцией точки A на плоскость π в направлении прямой l.
Таким образом, каждой точке A пространства сопоставляется ее проекция A' на плоскость π. Это соответствие называется параллельным проектированием на плоскость π в направлении прямой l.
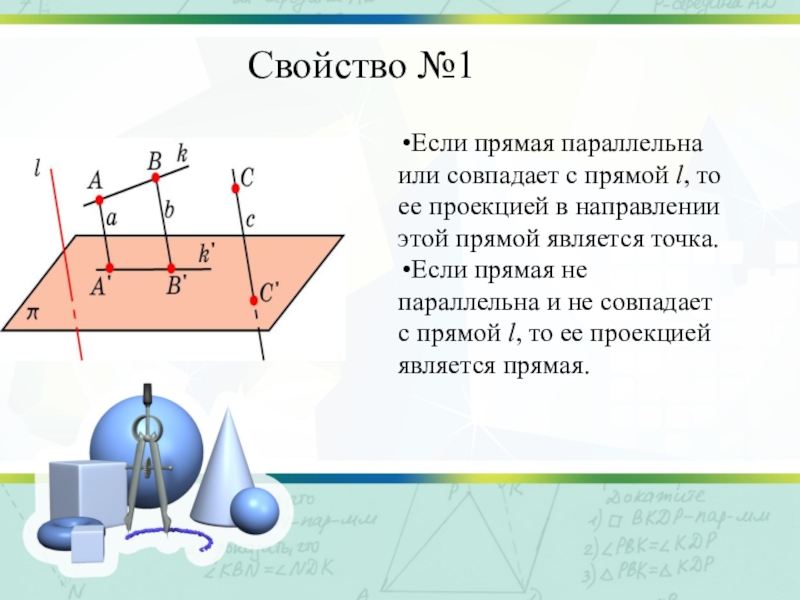
Слайд 4Свойство №1
Если прямая параллельна или совпадает с прямой l, то ее
проекцией в направлении этой прямой является точка.
Если прямая не параллельна и не совпадает с прямой l, то ее проекцией является прямая.
Если прямая не параллельна и не совпадает с прямой l, то ее проекцией является прямая.
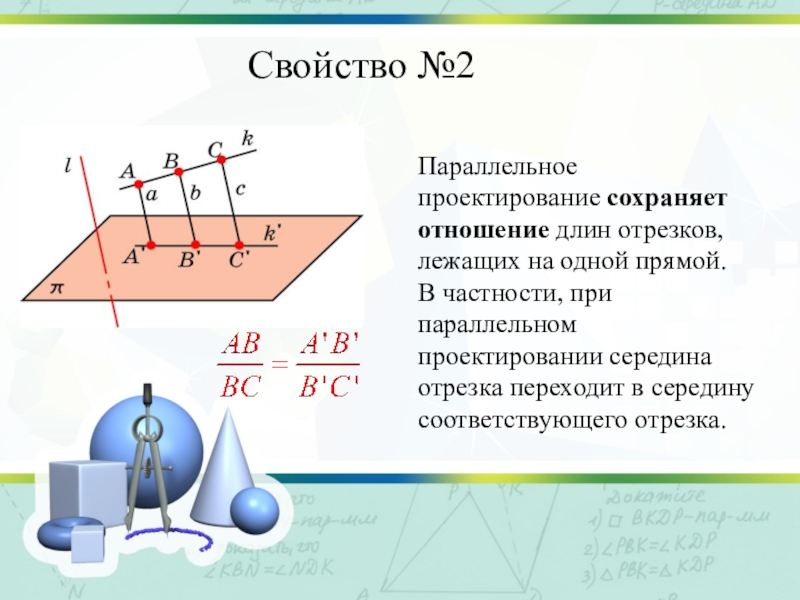
Слайд 5Свойство №2
Параллельное проектирование сохраняет отношение длин отрезков, лежащих на одной прямой.
В частности, при параллельном проектировании середина отрезка переходит в середину соответствующего отрезка.
Слайд 6Свойство №3
Если две параллельные прямые не параллельны прямой l, то их
проекциями в направлении l являются две параллельные прямые или одна прямая.
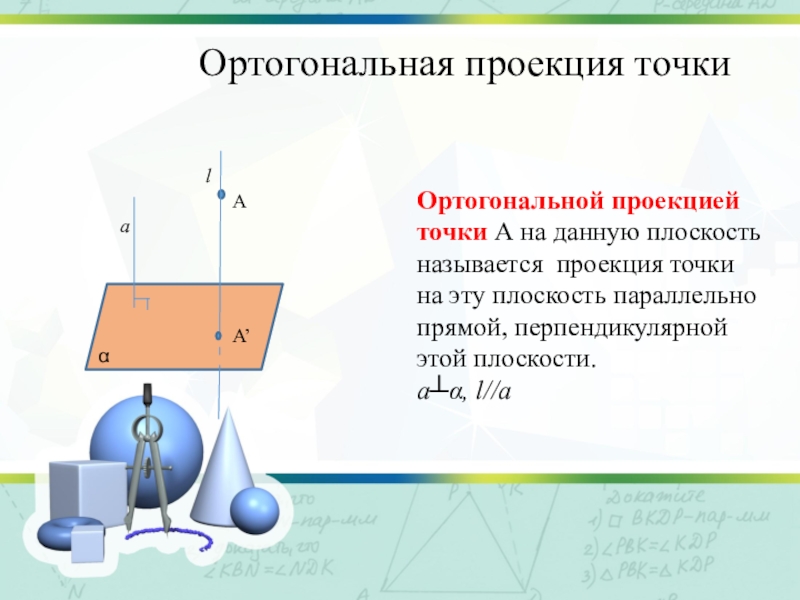
Слайд 7Ортогональная проекция точки
Ортогональной проекцией точки А на данную плоскость называется проекция
точки на эту плоскость параллельно прямой, перпендикулярной этой плоскости.
a┴α, l//a
a┴α, l//a
Слайд 8Ортогональная проекция фигуры
Ортогональной проекцией фигуры на данную плоскость состоит из ортогональных
проекций всех точек данной фигуры на эту плоскость. Ортогональная проекция используется при изображении пространственных тел на плоскости, особенно в технических чертежах. Она дает более реалистичное изображении, в отличии от произвольной параллельной проекции. Особенно круглых тел.
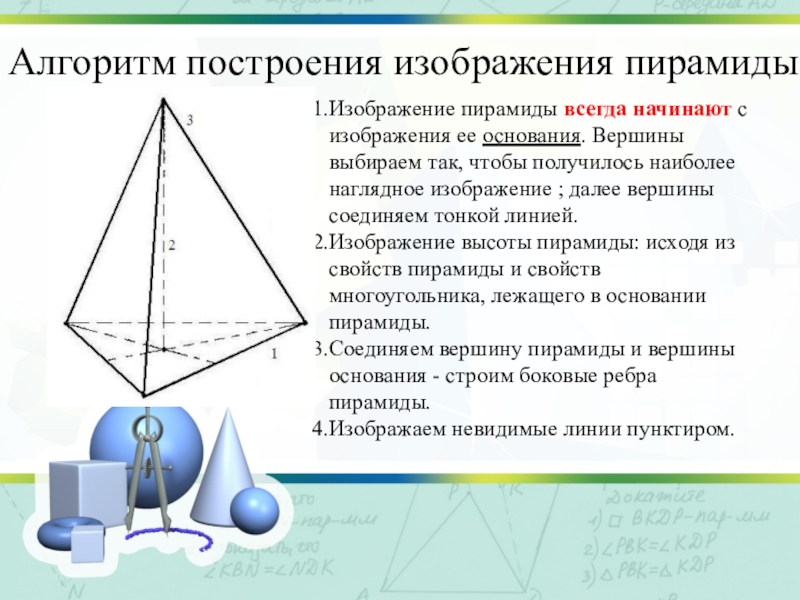
Слайд 15Алгоритм построения изображения пирамиды
Изображение пирамиды всегда начинают с изображения ее основания.
Вершины выбираем так, чтобы получилось наиболее наглядное изображение ; далее вершины соединяем тонкой линией.
Изображение высоты пирамиды: исходя из свойств пирамиды и свойств многоугольника, лежащего в основании пирамиды.
Соединяем вершину пирамиды и вершины основания - строим боковые ребра пирамиды.
Изображаем невидимые линии пунктиром.
Изображение высоты пирамиды: исходя из свойств пирамиды и свойств многоугольника, лежащего в основании пирамиды.
Соединяем вершину пирамиды и вершины основания - строим боковые ребра пирамиды.
Изображаем невидимые линии пунктиром.
Слайд 16Алгоритм изображения призмы
Изображение призмы всегда начинают с изображения ее основания. Вершины
выбираем так, чтобы получилось наиболее наглядное изображение ; далее вершины соединяем тонкой линией.
Изображение высоты призмы: исходя из свойств призмы и свойств многоугольника, лежащего в основании призмы.
Вершины верхней грани призмы соединяем с вершинами основания- строим боковые ребра пирамиды.
Изображаем невидимые линии пунктиром.
Изображение высоты призмы: исходя из свойств призмы и свойств многоугольника, лежащего в основании призмы.
Вершины верхней грани призмы соединяем с вершинами основания- строим боковые ребра пирамиды.
Изображаем невидимые линии пунктиром.
Слайд 17Домашнее задание
Записать опорный конспект согласно материалу из презентации.
Построить изображение пирамиды
в основании которой лежит правильный треугольник.
Построить изображение пирамиды в основании которой лежит прямоугольник.
Построить изображение призмы в основании которой лежит квадрат.
Построить изображение призмы в основании которой лежит равнобедренный треугольник.
Построить изображение призмы в основании которой лежит равнобедренная трапеция.
Ответьте на вопросы:
Что является параллельной проекцией отрезка, квадрата, треугольника?
Может ли при параллельном проецировании параллелограмма получиться трапеция и наоборот?
Построить изображение пирамиды в основании которой лежит прямоугольник.
Построить изображение призмы в основании которой лежит квадрат.
Построить изображение призмы в основании которой лежит равнобедренный треугольник.
Построить изображение призмы в основании которой лежит равнобедренная трапеция.
Ответьте на вопросы:
Что является параллельной проекцией отрезка, квадрата, треугольника?
Может ли при параллельном проецировании параллелограмма получиться трапеция и наоборот?