- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Магические квадраты
Содержание
- 1. Презентация по математике на тему Магические квадраты
- 2. Цель работы: Познакомится с историей появления магических
- 3. История появления магических квадратов. Трудно назвать такую
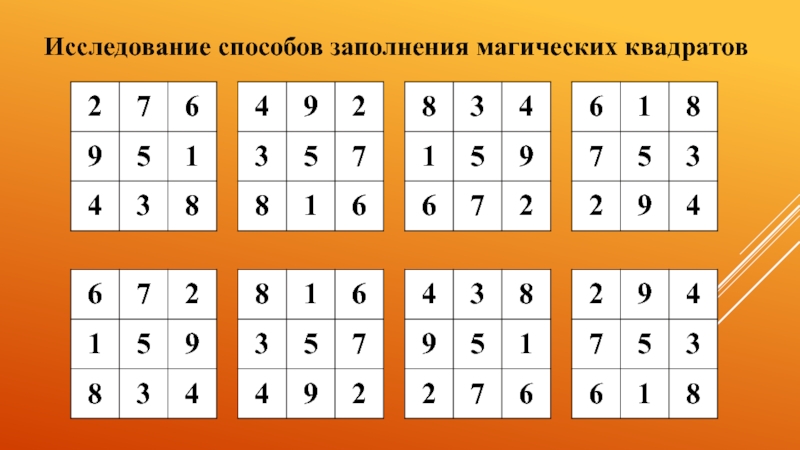
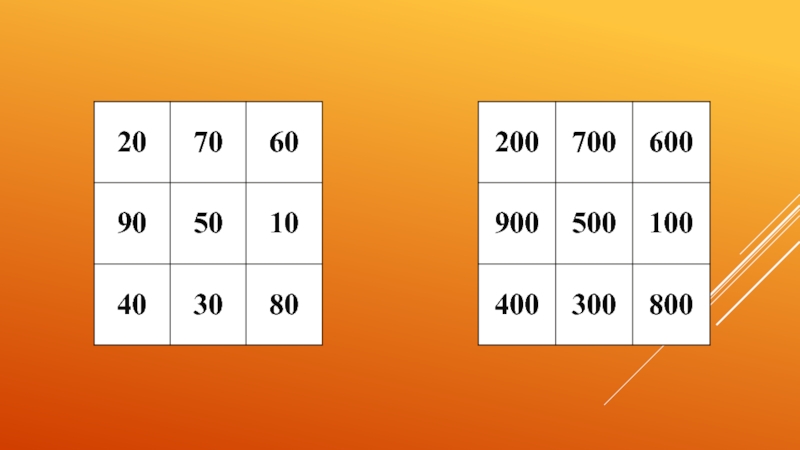
- 4. Исследование способов заполнения магических квадратов
- 5. Слайд 5
- 6. «Числа 2, 3, 4, 5, 6, 7,
- 7. Прослеживается закономерность: Сумма чисел по строкам, столбцам
- 8. Используя эти закономерности, определим сумму чисел в
- 9. Слайд 9
- 10. Составим магический квадрат с суммой чисел по
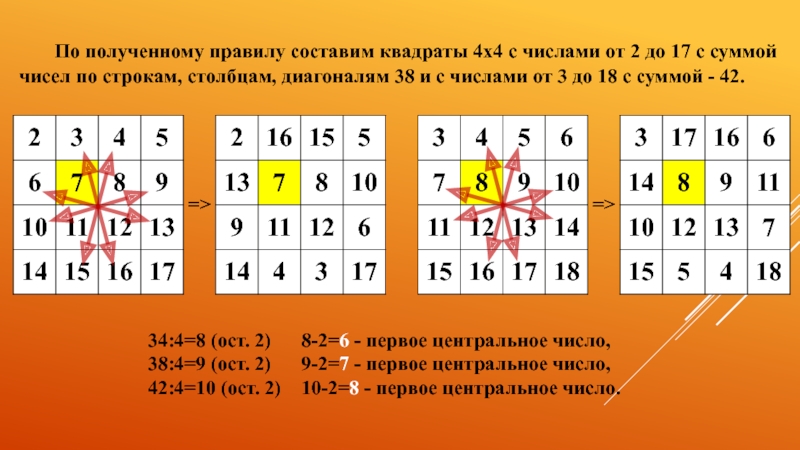
- 11. По полученному правилу составим квадраты 4х4 с
- 12. Квадрат 5х5. Сумма чисел в строках, столбцах,
- 13. Закономерность: магические квадраты с четным числом клеток
- 14. Найди значения выражений, впиши их в клетки
- 15. 2. 10 чисел, помеченные красным цветом, стоят
- 16. 3. На старой доске нарисован квадрат. В
- 17. В данной работе рассмотрены вопросы,
- 18. Спасибо за внимание !
Слайд 2Цель работы:
Познакомится с историей появления магических квадратов
Задачи:
Исследовать способы заполнения магических
Вывести алгоритм
Придумать применение магических квадратов
Актуальность:
Однажды, когда я ходил на олимпиаду, то одним из заданий был магический квадрат и мне захотелось узнать как можно больше о нём.
Гипотеза:
Для заполнения магического квадрата существуют специальные способы, позволяющие быстро это сделать.
Слайд 3История появления магических квадратов.
Трудно назвать такую отрасль человеческой деятельности, где
Слайд 6«Числа 2, 3, 4, 5, 6, 7, 8, 9 и 10
«Числа 2, 3, 4, 5, 6, 7, 8, 9 и 10 разместить в квадрате 3х3 так, чтобы сумма чисел по любой горизонтали, вертикали, и диагонали равнялось 18»
Слайд 7Прослеживается закономерность:
Сумма чисел по строкам, столбцам и диагоналям должна делиться
Частное от деления суммы чисел в строках, столбцах и диагоналях и 3-х будет стоять в центре квадрата и являться пятым числом в ряду натуральных чисел, которые необходимо найти
При делении суммы всех чисел в квадрате на 3 получается сумма чисел по строкам, столбцам и диагоналям
Слайд 8Используя эти закономерности, определим сумму чисел в строках, столбцах и диагоналях
1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16=136
136 : 4 = 34 – искомая сумма
Запишем эти числа в квадрате по порядку
Сумма чисел по диагоналям равна 34.
Остается поменять местами только числа 3, 4, 5, 6, 8, 9, 12, 14, 15
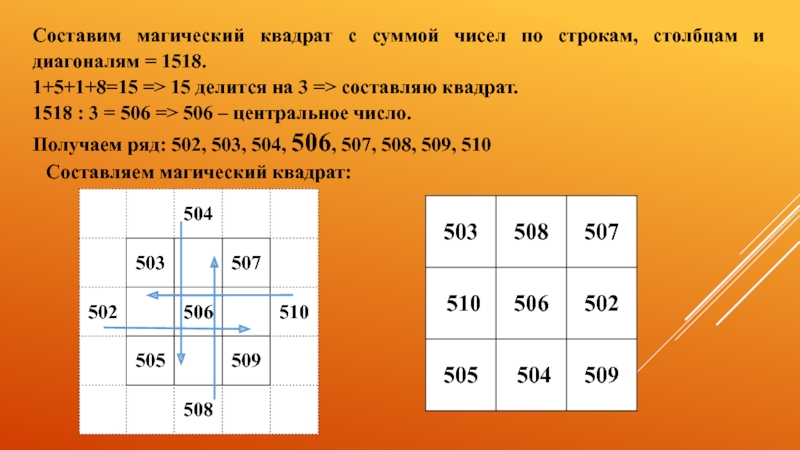
Слайд 10Составим магический квадрат с суммой чисел по строкам, столбцам и диагоналям
1+5+1+8=15 => 15 делится на 3 => составляю квадрат.
1518 : 3 = 506 => 506 – центральное число.
Получаем ряд: 502, 503, 504, 506, 507, 508, 509, 510
Составляем магический квадрат:
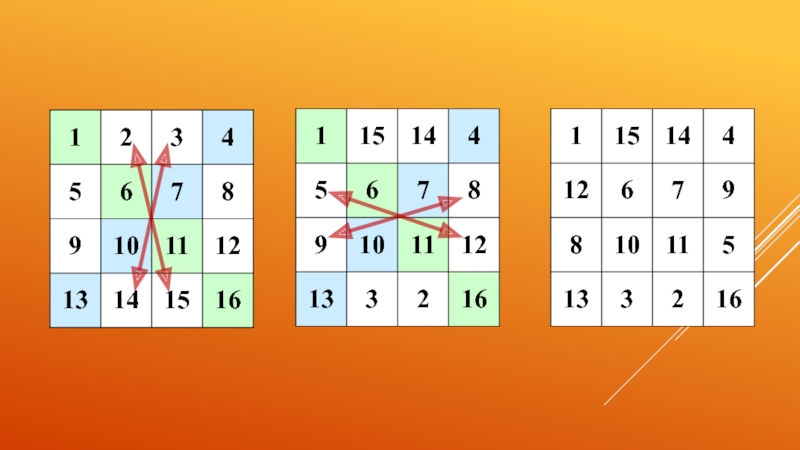
Слайд 11По полученному правилу составим квадраты 4х4 с числами от 2 до
34:4=8 (ост. 2) 8-2=6 - первое центральное число,
38:4=9 (ост. 2) 9-2=7 - первое центральное число,
42:4=10 (ост. 2) 10-2=8 - первое центральное число.
Слайд 12Квадрат 5х5. Сумма чисел в строках, столбцах, диагоналях в магическом квадрате:
65 : 5 = 13 – центральное число.
Записываем числа по порядку по диагоналям. Сумма по диагоналям в квадрате равна 65. Определяем расположение остальных чисел.
Слайд 13Закономерность: магические квадраты с четным числом клеток составляются по одной закономерности,
Магический квадрат с четным числом клеток:
Взять число, которое делится на количество клеток стороны квадрата с определенным остатком (деля количество клеток стороны на 2, получаем необходимый остаток).
От частного этого числа и стороны квадрата отнять остаток и получим 1-е центральное число.
Расставить числа в возрастающем и убывающем порядке по строкам.
По диагоналям числа остаются на месте, остальные меняются между собой.
Магический квадрат с нечетным числом клеток:
Сумма чисел по столбцам, строкам и диагоналям должна делиться на количество клеток одной стороны.
Частное от этого деления является центральным числом квадрата.
Предыдущие и последующие за центральным числа расставляются по порядку по диагоналям.
Пустые клетки заполняются числами, оказавшимися за квадратом
Слайд 14Найди значения выражений, впиши их в клетки квадрата с подходящими буквами
Математические задачи
Слайд 152. 10 чисел, помеченные красным цветом, стоят не на своих местах.
Слайд 163. На старой доске нарисован квадрат. В клетках этого квадрата должны
Слайд 17 В данной работе рассмотрены вопросы, связанные с историей развития
Несмотря на то, что собственно магические квадраты не нашли широкого применения в науке и технике, они подвигли на занятия математикой множество незаурядных людей и способствовали развитию других разделов математики: теории групп, определителей, матриц и др.