- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Конус
Содержание
- 1. Презентация по математике на тему Конус
- 2. Цель урока сегодня:Рассмотреть понятие конуса, усеченного конуса,
- 3. Окружность -Окружностью называется геометрическая фигура,состоящая из всех
- 4. Конусные фигуры в бытуФормы конуса в профессии «Повара, кондитера»
- 5. Конус -это тело, ограниченное конической поверхностью и кругом с границей L
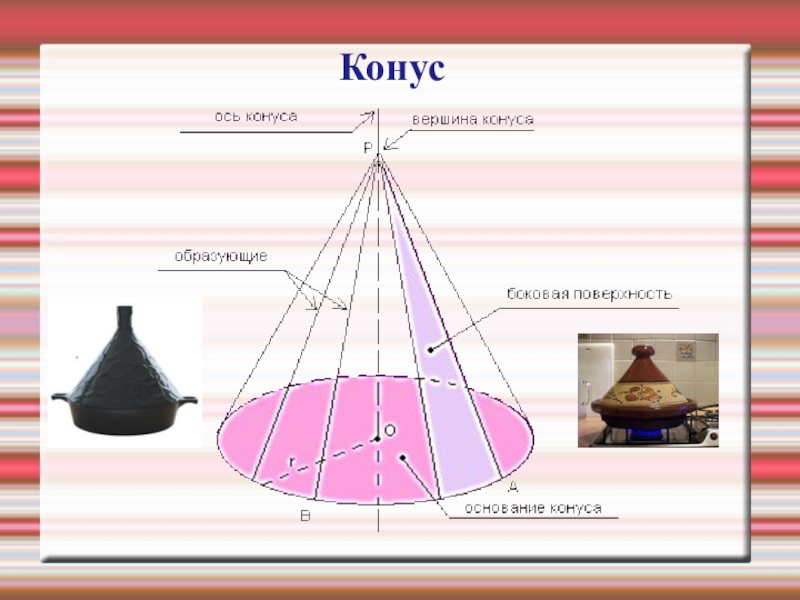
- 6. Конус
- 7. Конус получен вращением прямоугольного треугольника АВС вокруг катета АВ
- 8. Осевое сечение конуса Если секущая
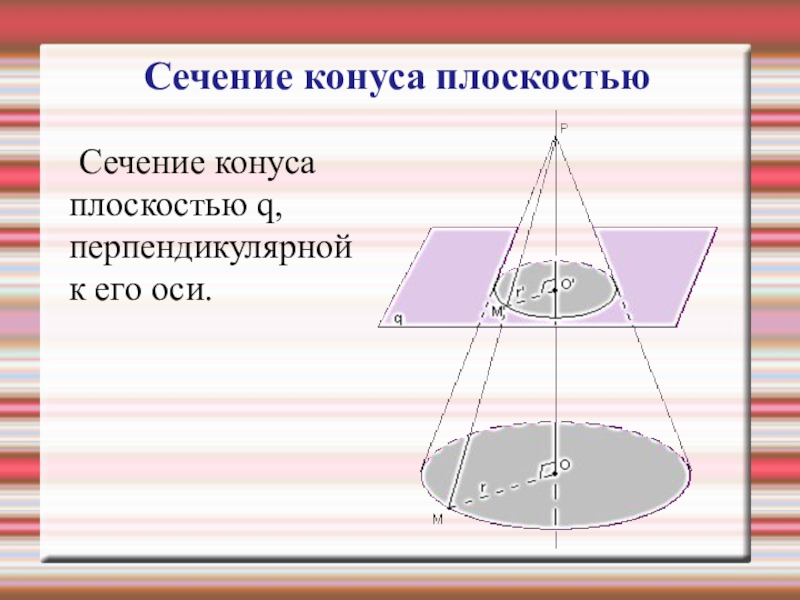
- 9. Сечение конуса плоскостью q, перпендикулярной
- 10. Площадь поверхности конусаЗа площадь боковой поверхности конуса
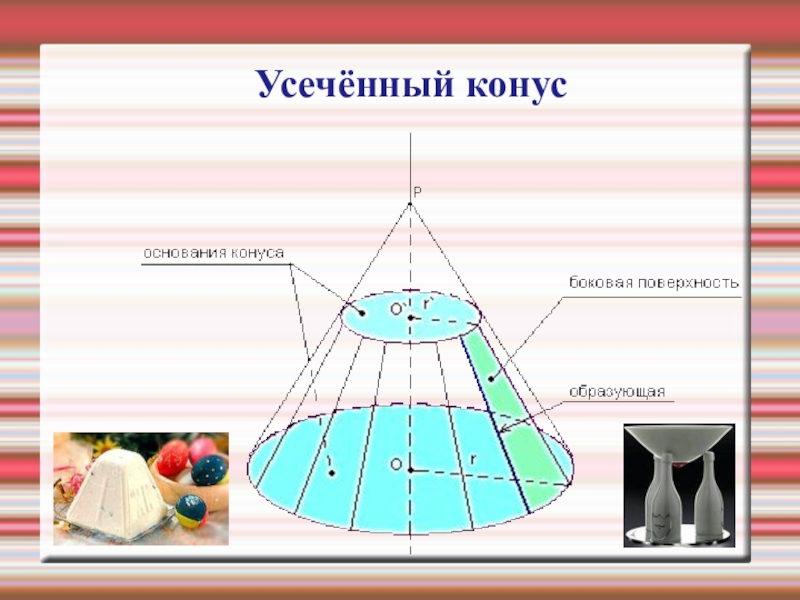
- 11. Усечённый конус
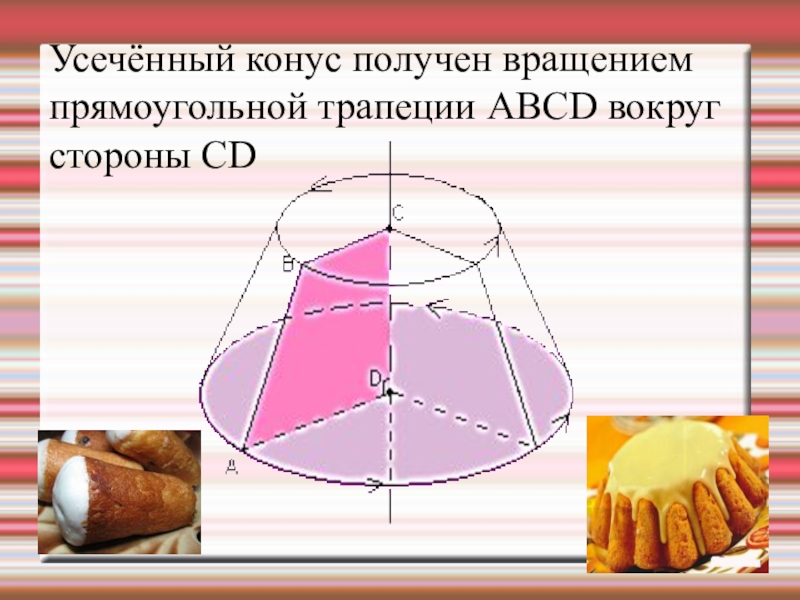
- 12. Усечённый конус получен вращением прямоугольной трапеции АВСD вокруг стороны CD
- 13. Площадь боковой поверхности усечённого конусаравна произведению полусуммы
- 14. Решение задач на нахождение площадей боковой и полной поверхности конуса, усечённого конуса rl
- 15. Решение задач на нахождение площадей боковой и
- 16. Подведем итог по теме:Что такое конус?При вращении
- 17. Спасибо за внимание!
Слайд 1
«Понятие конуса. Площадь поверхности конуса. Усеченный конус»
Разработала: Преподаватель математики Зайцева Светлана
Слайд 2Цель урока сегодня:
Рассмотреть понятие конуса, усеченного конуса, их элементов, научиться решению
Рассмотреть понятие площади боковой поверхности и полной поверхности конуса и усеченного конуса, научиться решать задачи на их нахождение
Слайд 3
Окружность -
Окружностью называется геометрическая фигура,состоящая из всех точек плоскости, расположенных на
Треугольник -
Геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, и соединяющих их отрезков
Слайд 8Осевое сечение конуса
Если секущая плоскость проходит через ось
Слайд 10
Площадь поверхности конуса
За площадь боковой поверхности конуса принимается площадь её развертки.
Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую. S=πrl
Площадь полной поверхности конуса- сумма площадей боковой поверхности и основания.S=πr(l+r)
Слайд 13Площадь боковой поверхности усечённого конуса
равна произведению полусуммы длин окружностей оснований на
S = π (r + r₁) l
Слайд 14Решение задач на нахождение площадей боковой и полной поверхности конуса, усечённого
r
l
Слайд 15Решение задач на нахождение площадей боковой и полной поверхности конуса, усечённого
Задача 2. Сколько потребуется посыпки на торт «Муравейник» диаметром основания 26 см, и высотой 15 см, если на каждый квадратный сантиметр ее требуется 3 г.
Рекомендации к решению: Торт «Муравейник» имеет форму конуса, вся посыпка представляет собой боковую поверхность. Зная диаметр найдем радиус, зная высоту и радиус найдем образующую, а затем и площадь боковой поверхности, т.е. площадь поверхности посыпки.
Слайд 16Подведем итог по теме:
Что такое конус?
При вращении какой фигуры получается конус,
3.Как надо пересечь конус плоскостью, чтобы в сечении получить: а) равнобедренный треугольник, б) круг.
4.Как получить усеченный конус из полного конуса?
5.Назовите основные элементы конуса, усеченного конуса.
6. Сформулируйте теорему Пифагора.
7.Как находится площадь:
а) боковой поверхности конуса?
б)Полной поверхности конуса?
в)Полной поверхности усеченного конуса?