№8 г. Ярцево Смоленской области
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии в 8 классе на тему прямоугольник
Содержание
- 1. Презентация по геометрии в 8 классе на тему прямоугольник
- 2. 1.Диагонали параллелограмма равны 7 дм и 4
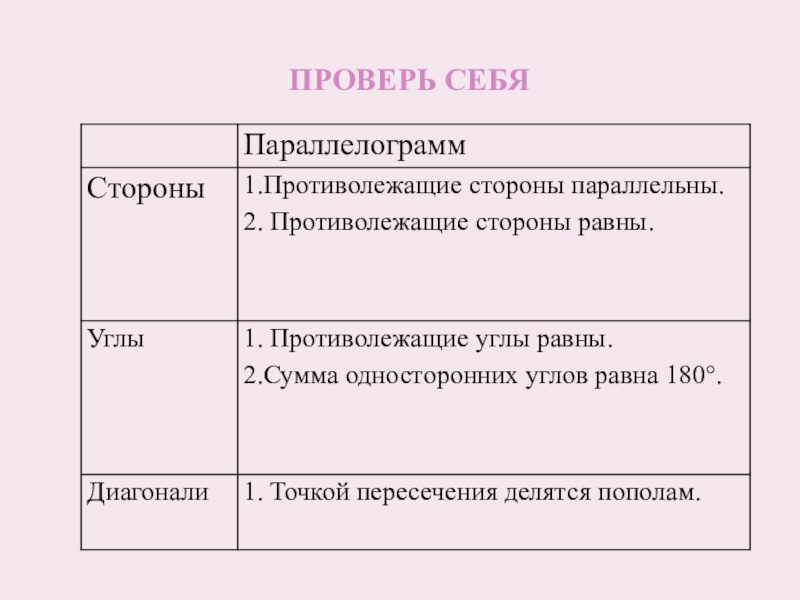
- 3. Работая в парах, заполнить таблицу о свойствах параллелограмма
- 4. ПРОВЕРЬ СЕБЯ
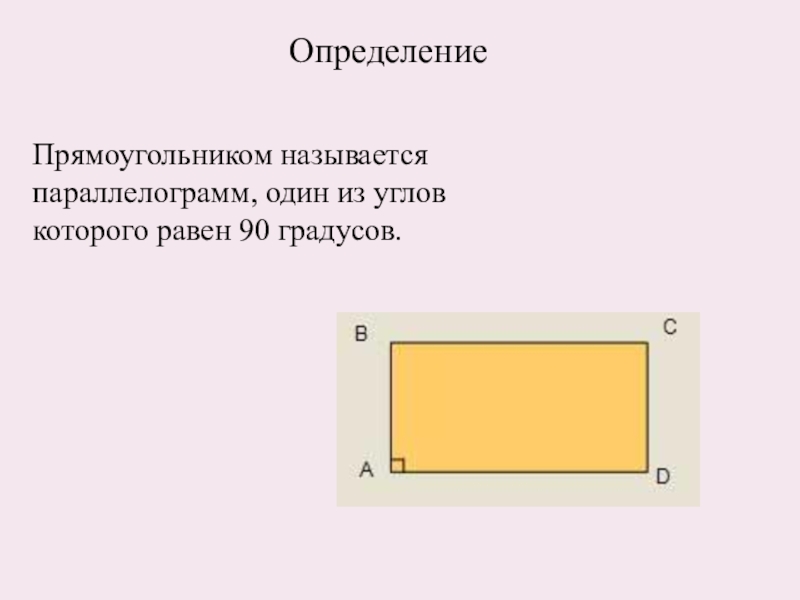
- 5. ОпределениеПрямоугольником называется параллелограмм, один из углов которого равен 90 градусов.
- 6. Прямоугольник в жизни
- 7. СУММА УГЛОВ ПРЯМОУГОЛЬНИКА
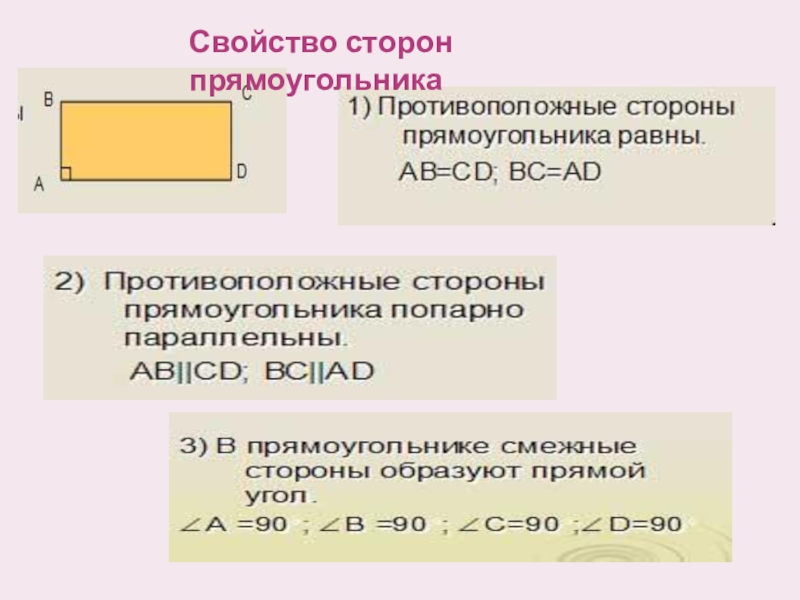
- 8. Свойство сторон прямоугольника
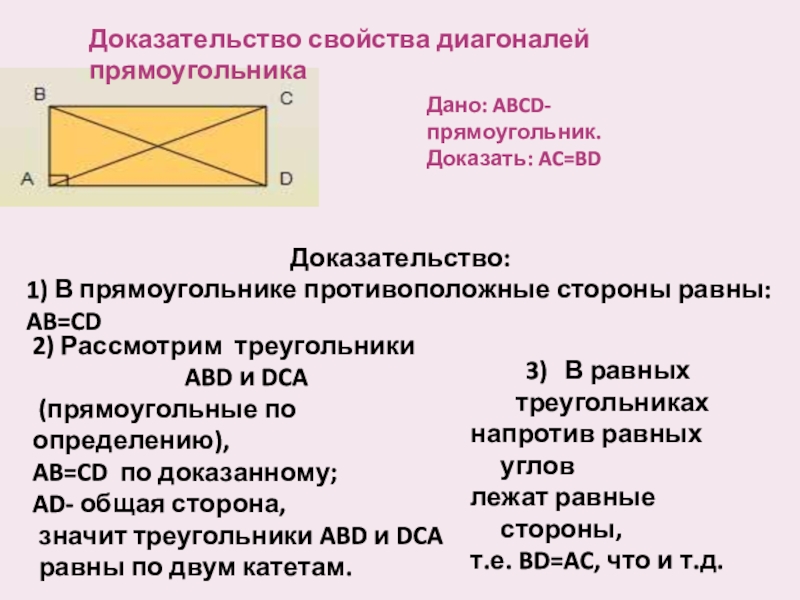
- 9. Доказательство свойства диагоналей прямоугольникаДано: ABCD- прямоугольник.Доказать: AC=BDДоказательство:1)
- 10. Доказательство:2). В равных треугольниках против равных сторон
- 11. Устное решение задач:А) Существует параллелограмм, у которого
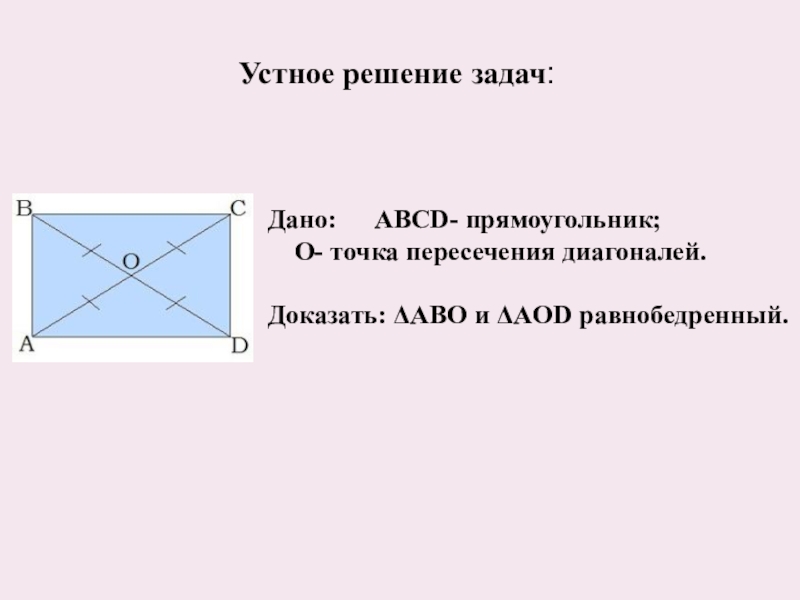
- 12. Д) Дано: ABCD- прямоугольник; O- точка пересечения
- 13. Устное решение задач: Дано: ABCD- прямоугольник; O- точка пересечения диагоналей. Доказать: ΔABO и ΔAOD равнобедренный.
- 14. Проверка заполнения таблицы
- 15. Слайд 15
1.Диагонали параллелограмма равны 7 дм и 4 дм(8 дм и 5 дм). На отрезки какой длины делит их точка пересечения?2. Один из углов параллелограмма равен 30° ( 145°).Найти остальные углы.3. Периметр параллелограмма 26 см (36 см)
Слайд 21.Диагонали параллелограмма равны 7 дм и 4 дм(8 дм и 5
дм).
На отрезки какой длины делит их точка пересечения?
На отрезки какой длины делит их точка пересечения?
2. Один из углов параллелограмма равен 30° ( 145°).
Найти остальные углы.
3. Периметр параллелограмма 26 см (36 см) ,
а одна из сторон равна 5 см (7см).
Найдите длины остальных сторон.
4. У параллелограмма все углы равны.
Найдите их градусную меру.
Математическский диктант
Слайд 5Определение
Прямоугольником называется
параллелограмм, один из углов
которого равен 90 градусов.
Слайд 9Доказательство свойства диагоналей прямоугольника
Дано: ABCD- прямоугольник.
Доказать: AC=BD
Доказательство:
1) В прямоугольнике противоположные стороны
равны: AB=CD
2) Рассмотрим треугольники
ABD и DCA
(прямоугольные по определению),
AB=CD по доказанному;
AD- общая сторона,
значит треугольники ABD и DCA
равны по двум катетам.
В равных
треугольниках
напротив равных углов
лежат равные стороны,
т.е. BD=AC, что и т.д.
Слайд 10Доказательство:
2). В равных треугольниках против равных сторон лежат соответственно
равные углы: ∠A=∠D и так как
∠A+∠D = 180° , то ∠А= 90°, значит, ABCD - прямоугольник
по определению, ч.т.д.
∠A+∠D = 180° , то ∠А= 90°, значит, ABCD - прямоугольник
по определению, ч.т.д.
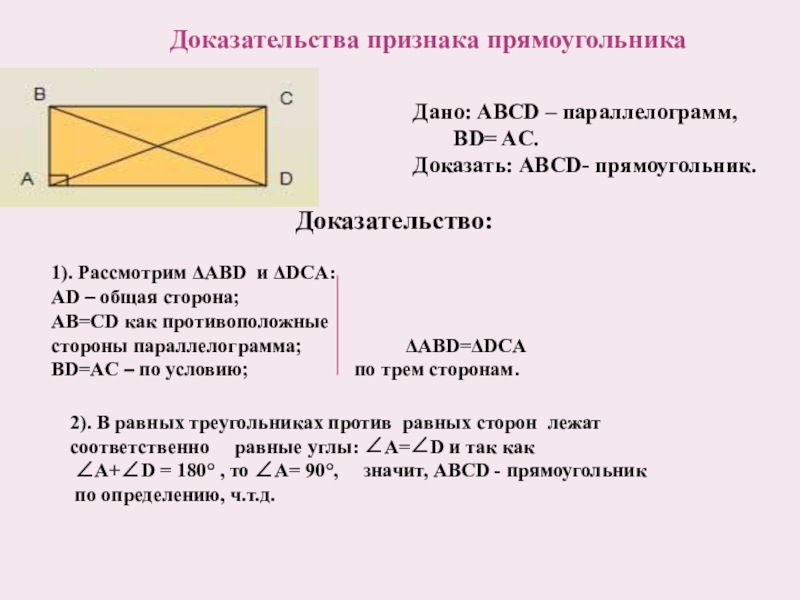
Дано: ABCD – параллелограмм,
BD= AC.
Доказать: ABCD- прямоугольник.
Доказательства признака прямоугольника
1). Рассмотрим ΔABD и ΔDCA:
AD – общая сторона;
AB=CD как противоположные
стороны параллелограмма; ΔABD=ΔDCA
BD=AC – по условию; по трем сторонам.
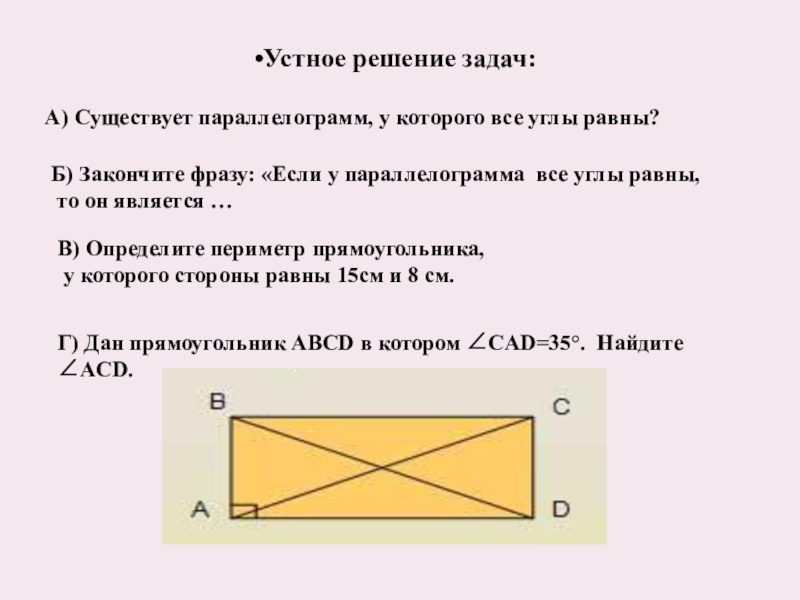
Слайд 11Устное решение задач:
А) Существует параллелограмм, у которого все углы равны?
Б) Закончите
фразу: «Если у параллелограмма все углы равны,
то он является …
то он является …
В) Определите периметр прямоугольника,
у которого стороны равны 15см и 8 см.
Г) Дан прямоугольник ABCD в котором ∠CAD=35°. Найдите ∠ACD.
Слайд 12Д)
Дано: ABCD- прямоугольник;
O- точка пересечения диагоналей.
Доказать: ΔABO и ΔAOD равнобедренный.
Слайд 13Устное решение задач:
Дано: ABCD- прямоугольник;
O- точка пересечения диагоналей.
Доказать: ΔABO
и ΔAOD равнобедренный.
