Подготовила учитель математики
Халилова Васпие Ибраимовна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии в 7 классе на тему Расстояние от точки до прямой
Содержание
- 1. Презентация по геометрии в 7 классе на тему Расстояние от точки до прямой
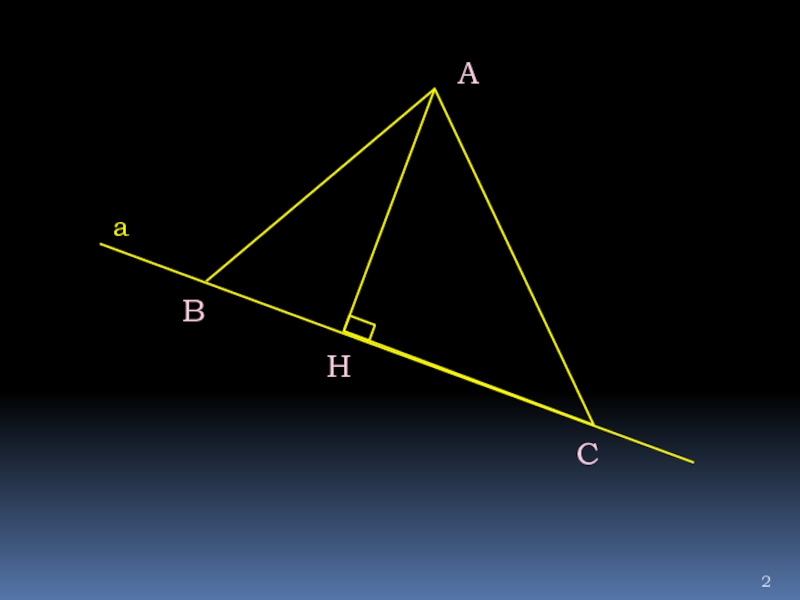
- 2. аАВНС
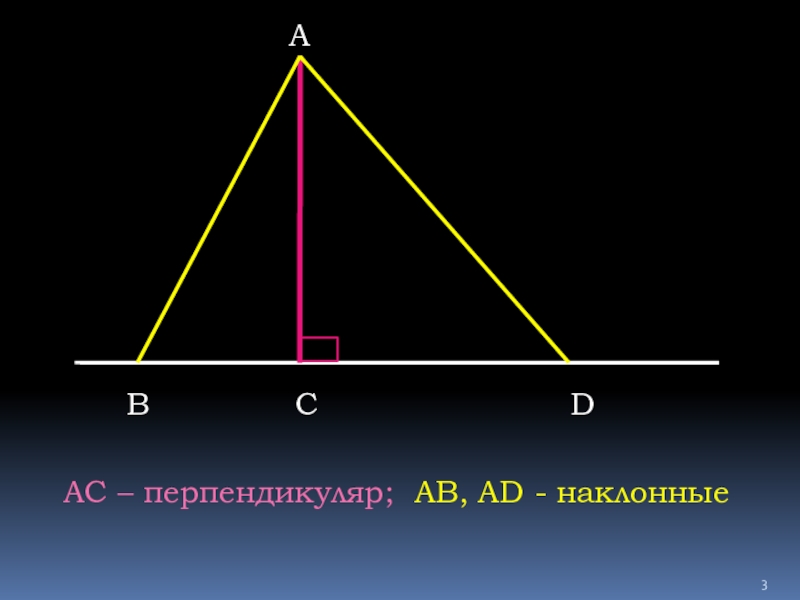
- 3. АВСDАС – перпендикуляр; АВ, AD - наклонные
- 4. Вывод:Перпендикуляр, проведённый из точки к прямой, меньше любой наклонной, проведённой из той же точки к прямой.
- 5. Определение:Длина перпендикуляра, проведённого из точки к прямой, называется расстоянием от этой точки до прямой.
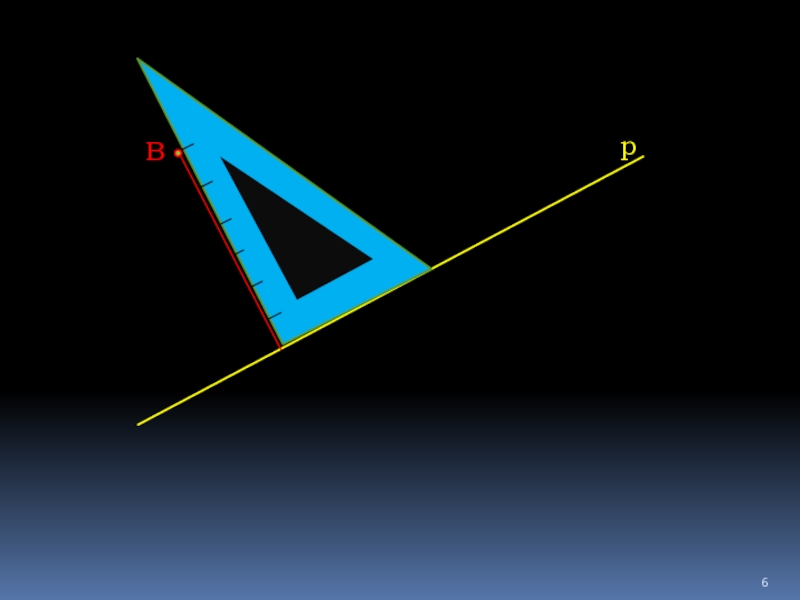
- 6. Вр
- 7. Теорема.Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
- 8. 12аbAXBYДоказательство:Так как XY ⊥ b, то XY
- 9. Определение:Расстояние от произвольной точки одной из параллельных прямых до другой прямой называется расстоянием между этими прямыми.
- 10. Теорема.Все точки плоскости, расположенные по одну сторону
- 11. АВаДоказать, что АВ ∥ аДоказательство:
- 12. Домашнее задание:§ 37, вопросы 14-18.2. Решить задачи № 272, 278.
аАВНС
Слайд 1Расстояние от точки до прямой.
Расстояние между параллельными прямыми.
Урок геометрии в
VII классе
Слайд 4Вывод:
Перпендикуляр, проведённый из точки к прямой, меньше любой наклонной, проведённой из
той же точки к прямой.
Слайд 5Определение:
Длина перпендикуляра, проведённого из точки к прямой, называется расстоянием от этой
точки до прямой.
Слайд 81
2
а
b
A
X
B
Y
Доказательство:
Так как XY ⊥ b, то XY ⊥ a. Прямоугольные треугольники
ABY и YXA равны по гипотенузе и острому углу ( AY – общая гипотенуза, а углы 1 и 2 равны как накрест лежащие углы при пересечении параллельных прямых a и b секущей AY ). Следовательно, XY = AB, что и требовалось доказать.
Доказать, что АВ = XY
Слайд 9Определение:
Расстояние от произвольной точки одной из параллельных прямых до другой прямой
называется расстоянием между этими прямыми.
Слайд 10Теорема.
Все точки плоскости, расположенные по одну сторону от данной прямой и
равноудалённые от неё, лежат на прямой, параллельной данной.
Слайд 11А
В
а
Доказать, что АВ ∥ а
Доказательство:
Так как
АС ⊥ а и BD ⊥ а, то АС ∥ BD, значит, накрест лежащие углы АСВ и СВD равны. ∆ АСВ = ∆ DBC по двум сторонам и углу между ними (АС = BD по условию теоремы, ВС – общая сторона, ∠АСВ = ∠CBD как накрест лежащие при параллельных прямых АС и BD и секущей ВС), следовательно, ∠АВС = ∠BCD.
∠АВС и ∠BCD – накрест лежащие углы при прямых АВ и СD и секущей ВС и они равны, следовательно, АВ ∥СD, т.е. АВ ∥ а, что и требовалось доказать.
∠АВС и ∠BCD – накрест лежащие углы при прямых АВ и СD и секущей ВС и они равны, следовательно, АВ ∥СD, т.е. АВ ∥ а, что и требовалось доказать.
С
D