- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии в 10 классе на тему Теорема о трех перпендикулярах
Содержание
- 1. Презентация по геометрии в 10 классе на тему Теорема о трех перпендикулярах
- 2. Самостоятельная работаВариант 1.Прямая АВ проходит через вершину
- 3. Проверка С.Р. По теме «Признак перпендикулярности прямой и плоскости»Prezentacii.com
- 4. Прямая АВ проходит через вершину В треугольника
- 5. Прямая MN проходит через вершину N треугольника
- 6. Перпендикуляр и наклоннаяНаклонная равна 16см, угол между
- 7. Теорема о трех перпендикулярахПрямая, проведенная в плоскости
- 8. Обратная теоремаПрямая, проведенная в плоскости через основание
Слайд 2Самостоятельная работа
Вариант 1.
Прямая АВ проходит через вершину В треугольника ВСD и
Вариант 2.
Прямая MN проходит через вершину N треугольника PNK и образует прямые углы со сторонами PN и NK. Докажите, что MN ⊥ PK.
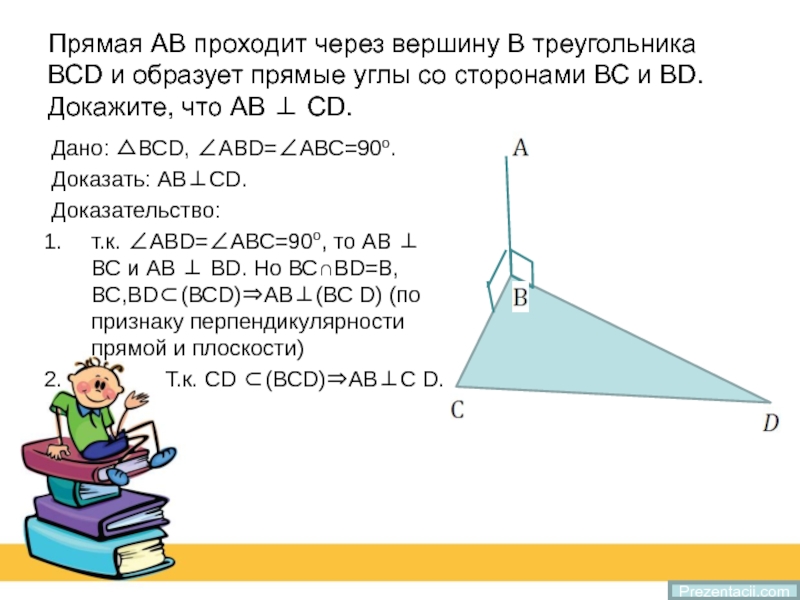
Слайд 4Прямая АВ проходит через вершину В треугольника ВСD и образует прямые
Дано: △ВСD, ∠АВD=∠АВС=90о.
Доказать: АВ⊥СD.
Доказательство:
т.к. ∠АВD=∠АВС=90о, то АВ ⊥ ВС и АВ ⊥ ВD. Но ВС∩ВD=В, ВС,BD⊂(ВСD)⇒АВ⊥(ВС D) (по признаку перпендикулярности прямой и плоскости)
Т.к. CD ⊂(ВСD)⇒АВ⊥С D.
Prezentacii.com
Слайд 5Прямая MN проходит через вершину N треугольника PNK и образует прямые
Дано: △PNK, ∠MNK=∠MNP=90о.
Доказать: MN⊥PK.
Доказательство:
т.к. ∠MNK=∠MNP=90о, то MN ⊥ NK и MN ⊥ PN. Но PN∩NK=N, PN,NK⊂(PNK)⇒MN⊥(PKN) (по признаку перпендикулярности прямой и плоскости)
Т.к. PK ⊂(PKN)⇒NM⊥PK.
Prezentacii.com
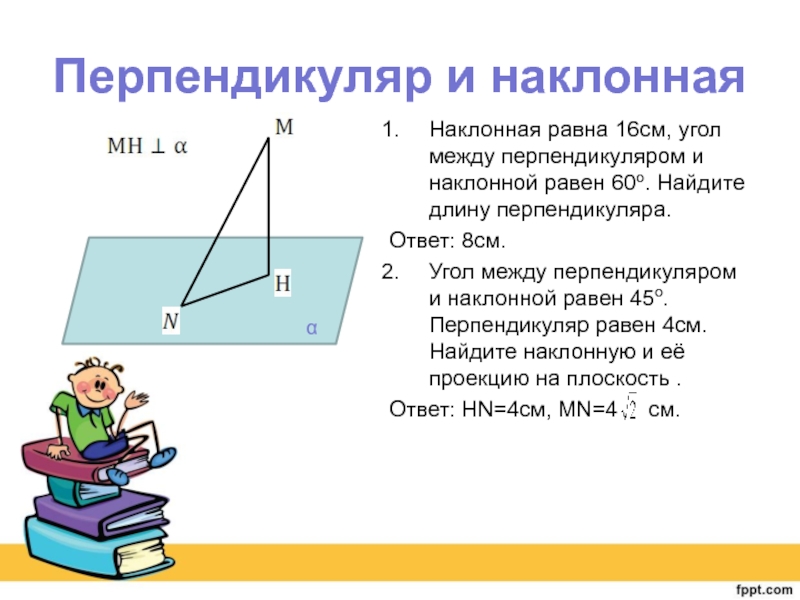
Слайд 6Перпендикуляр и наклонная
Наклонная равна 16см, угол между перпендикуляром и наклонной равен
Ответ: 8см.
Угол между перпендикуляром и наклонной равен 45о. Перпендикуляр равен 4см. Найдите наклонную и её проекцию на плоскость .
Ответ: HN=4см, MN=4 см.
α
Слайд 7Теорема о трех перпендикулярах
Прямая, проведенная в плоскости через основание наклонной перпендикулярно
Дано: АН⊥α,
АМ-наклонная,
НМ-её проекция,
а⊂α, М∊а, а⊥НМ.
Доказать: а⊥АМ.
Слайд 8Обратная теорема
Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней,
Дано: АН⊥α,
АМ-наклонная,
НМ-её проекция,
а⊂α, М∊а, а⊥АМ.
Доказать: а⊥НМ.