- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Тетраэдр (10 класс)
Содержание
- 1. Презентация по геометрии Тетраэдр (10 класс)
- 2. Входная диагностика уровня уровня имеющихся знаний по данной теме:
- 3. Цели и задачи проекта:Узнать типы и свойства
- 4. Тетра́эдр (греч. четырёхгранник) — простейший многогранник, гранями которого
- 5. 1) Отрезок, соединяющий середины противоположных ребер тетраэдра,
- 6. Формулы для правильного тетраэдра:Площадь полной поверхностиПравильный тетраэдр-тетраэдр,
- 7. В тетраэдре DABC дано: угол ADB =54,
- 8. Применение тетраэдров: Тетраэдр образует жёсткую, статически определимую конструкцию.
- 9. Тетраэдры в природе:Некоторые плоды, находясь вчетвером на
- 10. Выводы:
Входная диагностика уровня уровня имеющихся знаний по данной теме:
Слайд 1Тетраэдр
Презентация к урокам геометрии.
Каторова О.Г.,
учитель математики
МБОУ Гимназии № 2
города Сарова
Слайд 3Цели и задачи проекта:
Узнать типы и свойства тетраэдров.
Представить модель тетраэдра.
Применение тетраэдра
в практической деятельности человека.
Решение задач, связанных с тетраэдром.
Решение задач, связанных с тетраэдром.
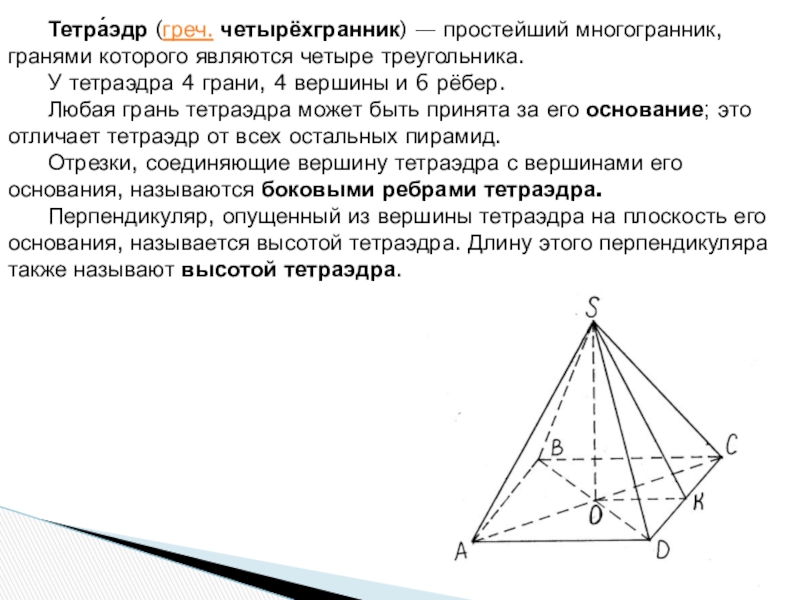
Слайд 4 Тетра́эдр (греч. четырёхгранник) — простейший многогранник, гранями которого являются четыре треугольника.
У
тетраэдра 4 грани, 4 вершины и 6 рёбер.
Любая грань тетраэдра может быть принята за его основание; это отличает тетраэдр от всех остальных пирамид.
Отрезки, соединяющие вершину тетраэдра с вершинами его основания, называются боковыми ребрами тетраэдра.
Перпендикуляр, опущенный из вершины тетраэдра на плоскость его основания, называется высотой тетраэдра. Длину этого перпендикуляра также называют высотой тетраэдра.
Любая грань тетраэдра может быть принята за его основание; это отличает тетраэдр от всех остальных пирамид.
Отрезки, соединяющие вершину тетраэдра с вершинами его основания, называются боковыми ребрами тетраэдра.
Перпендикуляр, опущенный из вершины тетраэдра на плоскость его основания, называется высотой тетраэдра. Длину этого перпендикуляра также называют высотой тетраэдра.
Слайд 51) Отрезок, соединяющий середины противоположных ребер тетраэдра, называется бимедианой тетраэдра (бимедианы
FK,HT,LN). Все бимедианы тетраэдра пересекаются в одной точке и делятся ею пополам.
2) Отрезок, соединяющий вершину тетраэдра с центроидом (точка пересечения его медиан) противолежащей грани, называется медианой этого тетраэдра(РH1)
3) Точка пересечения медиан тетраэдра совпадает с точкой пересечения его бимедиан.
2) Отрезок, соединяющий вершину тетраэдра с центроидом (точка пересечения его медиан) противолежащей грани, называется медианой этого тетраэдра(РH1)
3) Точка пересечения медиан тетраэдра совпадает с точкой пересечения его бимедиан.
Тетраэдр (свойства) :
Слайд 6Формулы для правильного тетраэдра:
Площадь полной поверхности
Правильный тетраэдр-тетраэдр, у которого все грани
– правильные треугольники.
Объем
Высота
Другие виды тетраэдров:
Прямоугольный тетраэдр, у которого все ребра, прилежащие к одной из вершин, перпендикулярны между собой
Равногранный тетраэдр, у которого все грани — равные между собой треугольники.
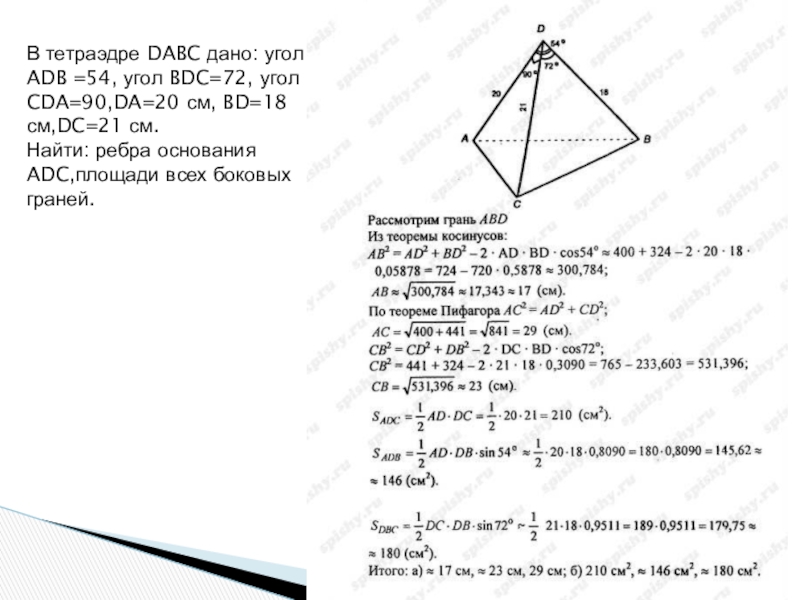
Слайд 7В тетраэдре DABC дано: угол ADB =54, угол BDC=72, угол CDA=90,DA=20
см, BD=18 см,DC=21 см.
Найти: ребра основания ADC,площади всех боковых граней.
Найти: ребра основания ADC,площади всех боковых граней.
Слайд 8Применение тетраэдров:
Тетраэдр образует жёсткую, статически определимую конструкцию. Тетраэдр, выполненный из стержней,
часто используется в качестве основы для пространственных несущих конструкций пролётов зданий, перекрытий, балок, ферм, мостов и т. д. Стержни испытывают только продольные нагрузки.
Прямоугольный тетраэдр используется в оптике. Если грани, имеющие прямой угол, покрыть светоотражающим составом или весь тетраэдр выполнить из материала с сильным светопреломлением, чтобы возникал эффект полного внутреннего отражения, то свет, направленный в грань, противоположную вершине с прямыми углами, будет отражаться в том же направлении, откуда он пришёл. Это свойство используется для создания уголковых отражателей.
Прямоугольный тетраэдр используется в оптике. Если грани, имеющие прямой угол, покрыть светоотражающим составом или весь тетраэдр выполнить из материала с сильным светопреломлением, чтобы возникал эффект полного внутреннего отражения, то свет, направленный в грань, противоположную вершине с прямыми углами, будет отражаться в том же направлении, откуда он пришёл. Это свойство используется для создания уголковых отражателей.
Слайд 9Тетраэдры в природе:
Некоторые плоды, находясь вчетвером на одной кисти, располагаются в
вершинах тетраэдра, близкого к правильному. Такая конструкция обусловлена тем, что центры четырёх одинаковых шаров, касающихся друг друга, находятся в вершинах правильного тетраэдра. Поэтому похожие на шар плоды образуют подобное взаимное расположение. Например, таким образом могут располагаться грецкие орехи.