- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Синус, косинус 8 класс
Содержание
- 1. Презентация по геометрии Синус, косинус 8 класс
- 2. Цели урокаНаучить учащихся вычислять значения синуса, косинуса
- 3. СодержаниеПроверка домашнего заданияУстная работаВычисление значений синуса, косинуса
- 4. Проверка домашнего заданияЗадача № 591(в) Дано:ΔАВС∠С=900ВС=1 АС=2
- 5. Проверка домашнего задания Ответы к тесту:А2) А3) В4) Б5) Б
- 6. Устная работа1. Сформулируйте теорему Пифагора для прямоугольного
- 7. Устная работаДано:ΔАВС∠С=900ВС=5 АВ=13 Найти:Sin A, cos A, tg A,Sin B, cos B, tg B.
- 8. Решение задачиПо теореме Пифагора:АВ2=ВС2+АС2АС2=169-25АС2=144АС=12SIN A=BCABCOS A=ACABtg A=BCACSIN B =ACABCOS B=BCABtg B =ACBC
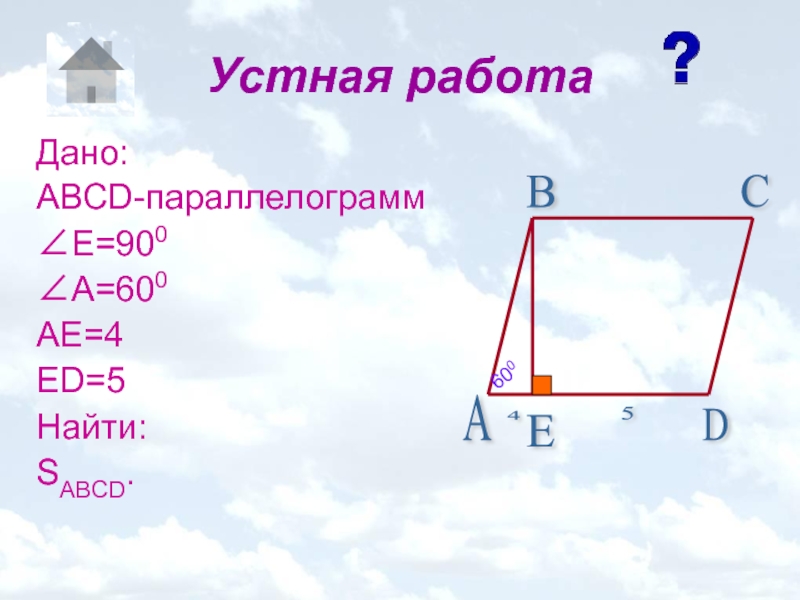
- 9. Устная работаДано:АВСD-параллелограмм∠E=900∠A=600AE=4 ED=5Найти:SABCD.
- 10. Решение задачиПо теореме Пифагора:AB2=AE2+BE2BE2=64-16=48∠ABE=300SABCD=BE·ADAD=4+5=9AE=0,5∙AB => AB=8
- 11. Вычисление значений синуса, косинуса и тангенса для
- 12. Решение задачи №1Пусть ВС=х тогда АВ=2х 300
- 13. Вычисление значений синуса, косинуса и тангенса для
- 14. Решение задачи №2Пусть ВС=х тогда АC=х => SIN 450=> tg 450=> COS 450
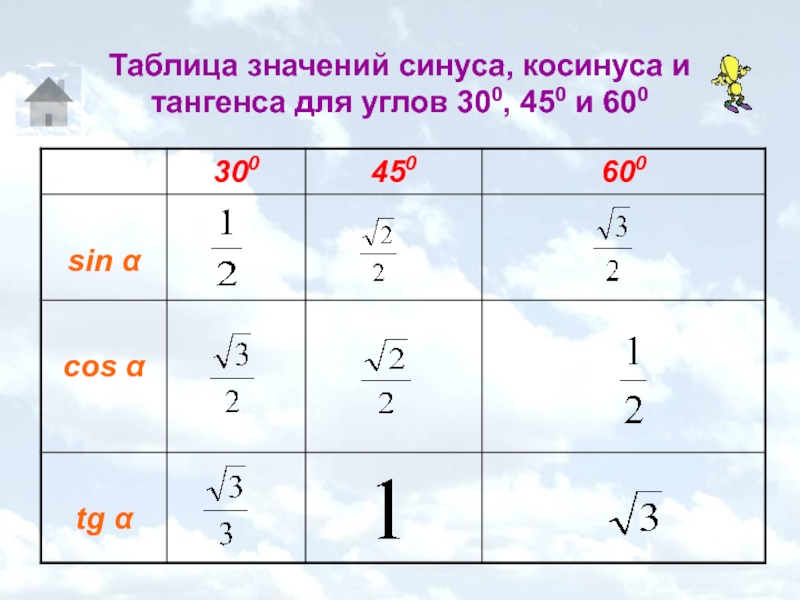
- 15. Таблица значений синуса, косинуса и тангенса для углов 300, 450 и 600
- 16. Решение задачЗадача №3 В прямоугольной трапеции основания
- 17. Решение задачи №3Проведем ВН⊥ADBH=CD=4 AH=AD – HD=5 ΔABH-прямоугольныйПО ТЕОРЕМЕ ПИФАГОРА:АВ2=ВН2+АН2
- 18. Решение задач В прямоугольном треугольнике гипотенуза
- 19. Решение задачи №4ΔABС-прямоугольный∠В=900-α∠В=300, так как α=600=> ВС=АВ∙SIN
- 20. Итоги урокаКак найти острый угол прямоугольного треугольника,
- 21. Итоги урока3. Как взаимосвязаны два катета прямоугольного
- 22. Домашнее заданиеВыучить значения синуса, косинуса и тангенса
Слайд 2Цели урока
Научить учащихся вычислять значения синуса, косинуса и тангенса для углов
Формировать навыки решения прямоугольных треугольников, используя синус, косинус и тангенс острого угла.
Слайд 3Содержание
Проверка домашнего задания
Устная работа
Вычисление значений синуса, косинуса и тангенса для углов
Таблица значений синуса, косинуса и тангенса для углов 300, 450 и 600
Решение задач
Итоги урока
Домашнее задание
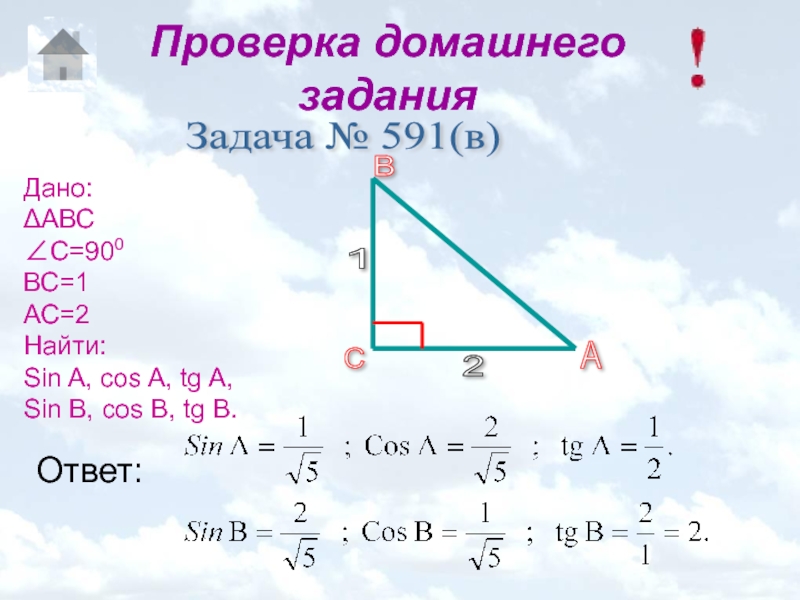
Слайд 4Проверка домашнего задания
Задача № 591(в)
Дано:
ΔАВС
∠С=900
ВС=1
АС=2
Найти:
Sin A, cos A,
Sin B, cos B, tg B.
Ответ:
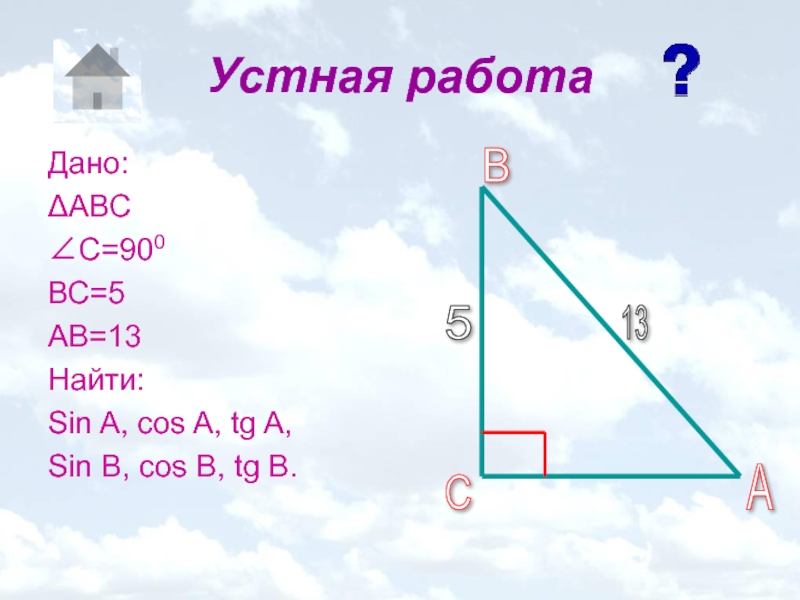
Слайд 6Устная работа
1. Сформулируйте теорему Пифагора для прямоугольного треугольника.
2.Что называют синусом, косинусом,
3. Как найти площадь параллелограмма?
4. Как найти катет прямоугольного треугольника, лежащий напротив угла в 300?
C2=a2+b2
S=a∙h
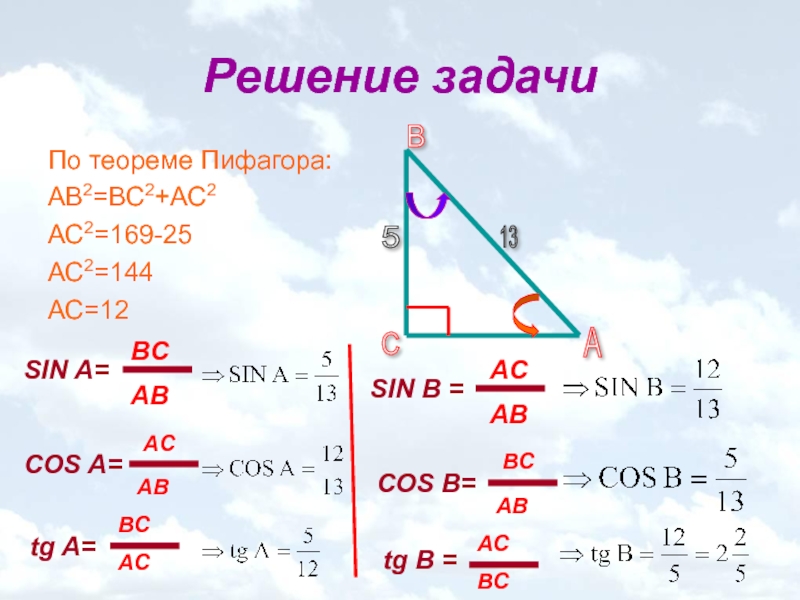
Слайд 8Решение задачи
По теореме Пифагора:
АВ2=ВС2+АС2
АС2=169-25
АС2=144
АС=12
SIN A=
BC
AB
COS A=
AC
AB
tg A=
BC
AC
SIN B =
AC
AB
COS B=
BC
AB
tg B
AC
BC
Слайд 10Решение задачи
По теореме Пифагора:
AB2=AE2+BE2
BE2=64-16=48
∠ABE=300
SABCD=BE·AD
AD=4+5=9
AE=0,5∙AB => AB=8
Слайд 11Вычисление значений синуса, косинуса и тангенса для углов 300, 450 и
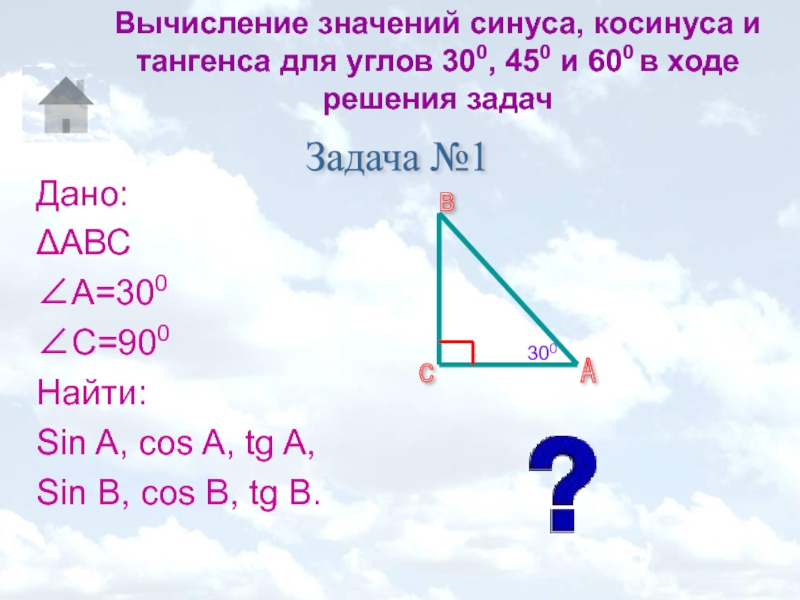
Дано:
ΔАВС
∠А=300
∠С=900
Найти:
Sin A, cos A, tg A,
Sin B, cos B, tg B.
Задача №1
300
Слайд 13Вычисление значений синуса, косинуса и тангенса для углов 300, 450 и
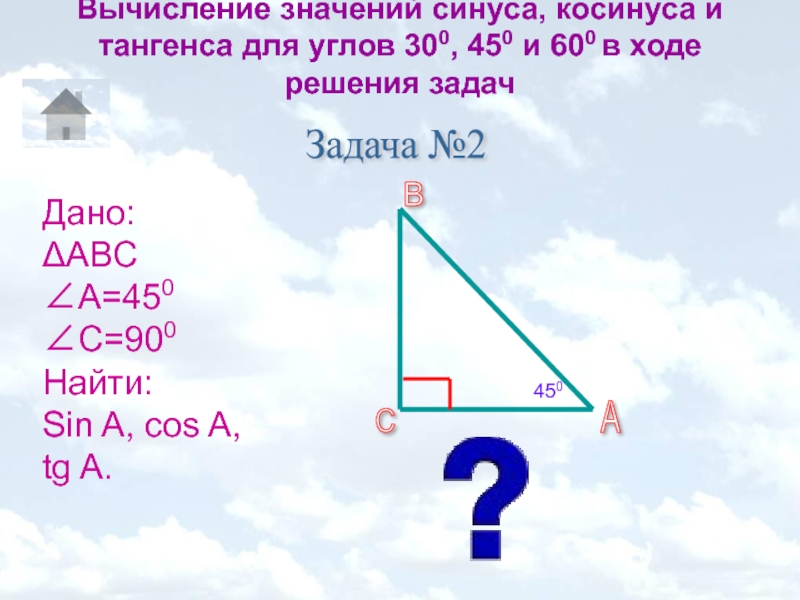
Задача №2
Дано:
ΔАВС
∠А=450
∠С=900
Найти:
Sin A, cos A, tg A.
Слайд 16Решение задач
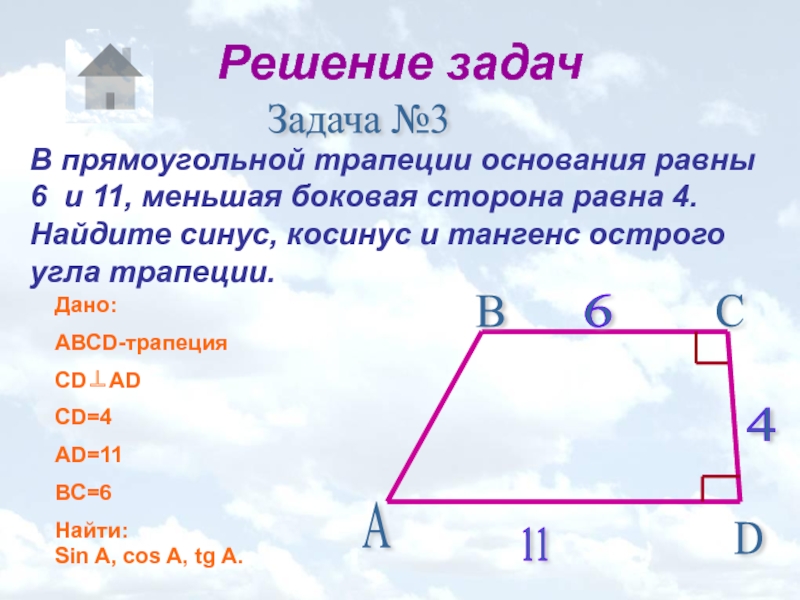
Задача №3
В прямоугольной трапеции основания равны 6 и 11,
Дано:
АВСD-трапеция
CD⊥AD
CD=4
AD=11
BC=6
Найти:
Sin A, cos A, tg A.
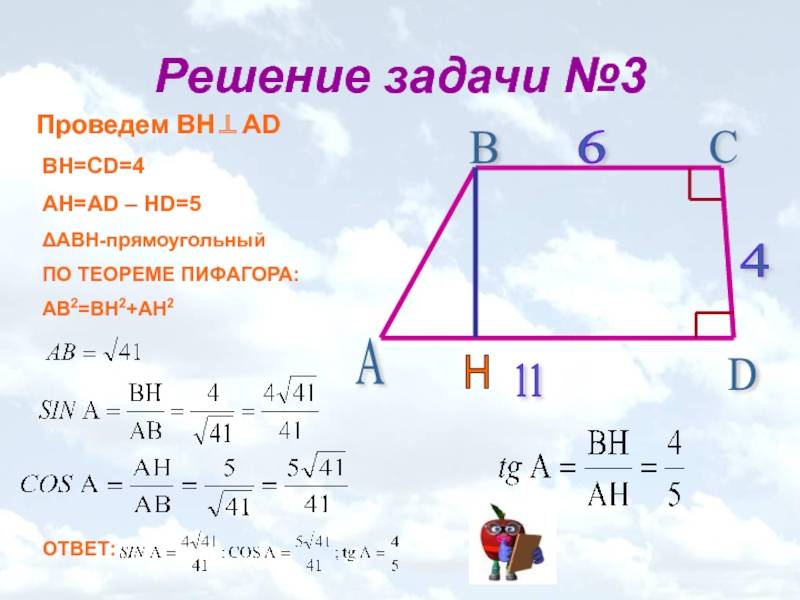
Слайд 17Решение задачи №3
Проведем ВН⊥AD
BH=CD=4
AH=AD – HD=5
ΔABH-прямоугольный
ПО ТЕОРЕМЕ ПИФАГОРА:
АВ2=ВН2+АН2
Слайд 18Решение задач
В прямоугольном треугольнике гипотенуза равна с, а один
Задача № 4
Дано:
ΔАВС
∠А=α=600
AВ=24
Найти:
∠В, АС, ВС,
Выразить через
α и с.
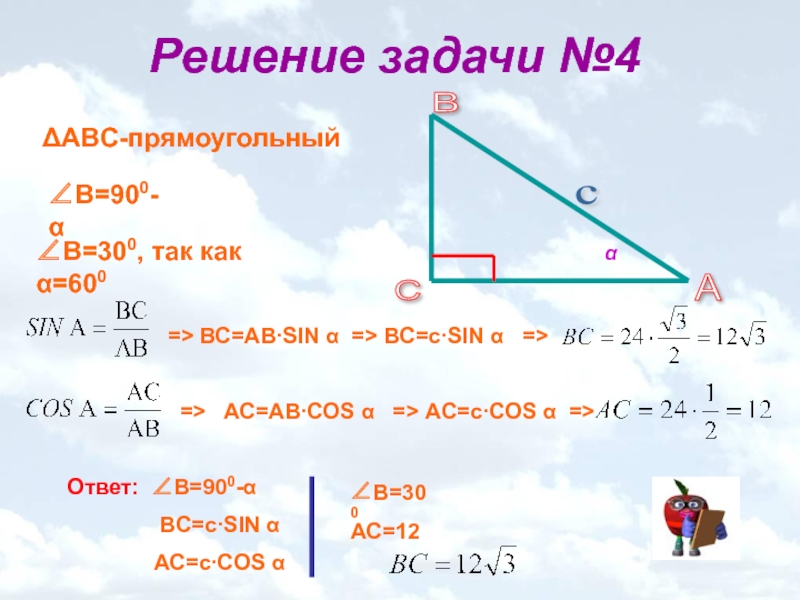
Слайд 19Решение задачи №4
ΔABС-прямоугольный
∠В=900-α
∠В=300, так как α=600
=> ВС=АВ∙SIN α => BС=c∙SIN α
=> AС=АВ∙COS α => AС=c∙COS α =>
Ответ: ∠В=900-α
BС=c∙SIN α
AС=c∙COS α
∠В=300
АС=12
Слайд 20Итоги урока
Как найти острый угол прямоугольного треугольника, если другой острый угол
2. Какая связь существует между катетом, противолежащим ему углом и гипотенузой?
Слайд 21Итоги урока
3. Как взаимосвязаны два катета прямоугольного треугольника и один из
4. Какая связь существует между катетом, прилежащим к нему острым углом и гипотенузой?
5. Для каких углов сегодня узнали значения синуса, косинуса и тангенса?
Слайд 22Домашнее задание
Выучить значения синуса, косинуса и тангенса для углов 300, 450
№ 595; № 597; № 598(б).