Презентация, доклад по теме прямоугольный треугольник для итогового повторения в 9 классе

Содержание

1. Презентация по теме прямоугольный треугольник для итогового повторения в 9 классе
2. Признаки равенстваАВСA1B1 C1 По двум катетам.По катету
3. Признаки подобияАВСA1B1 C1 ΔABC ∞ Δ A1B1C1
4. Теорема ПифагораСумма квадратов катетов равна квадрату гипотенузы:Справедливо
5. Соотношения между сторонами и углами аbcαβ)))проверь себя
6. Свойства проекций катетовabchВысота, опущенная на гипотенузу, является
7. Вписанная окружностьabcrРадиус вписанной окружностиr, он равен:Длина гипотенузы
8. Описанная окружностьabcROГипотенуза прямоугольного треугольника является диаметром окружности,
9. Площадь треугольника аbcαβ)))

Признаки равенстваАВСA1B1 C1 По двум катетам.По катету и гипотенузе.По катету и прилежащему острому углу.По катету и противолежащему острому углу.По гипотенузе и острому углу.

Главная
Геометрия
Презентация по теме прямоугольный треугольник для итогового повторения в 9 классе

Слайд 1Прямоугольный треугольник
Треугольник, у которого один угол прямой, называется прямоугольным.
Сторона, лежащая против

прямого угла, называется гипотенузой (АВ).
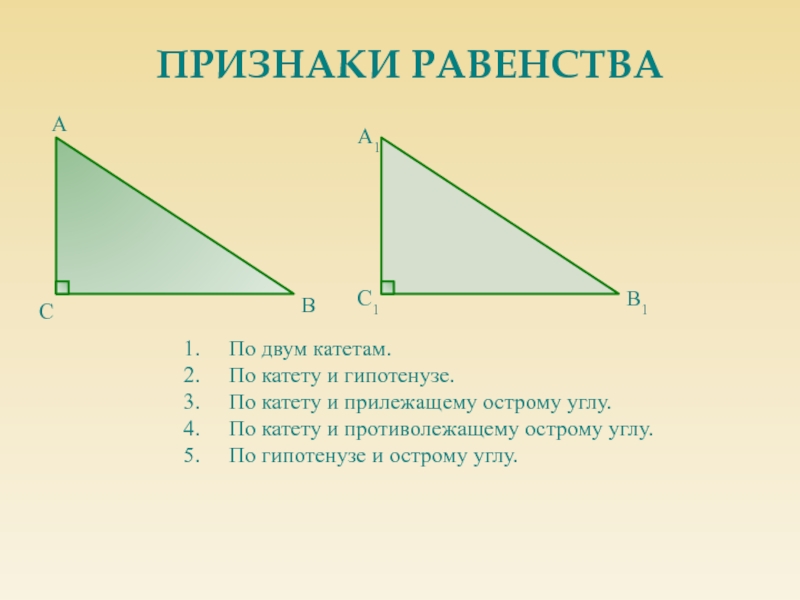
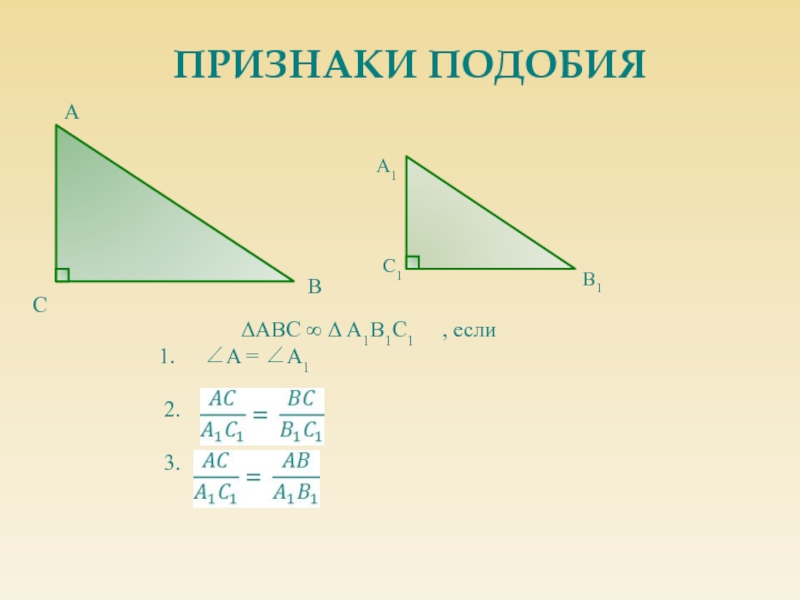
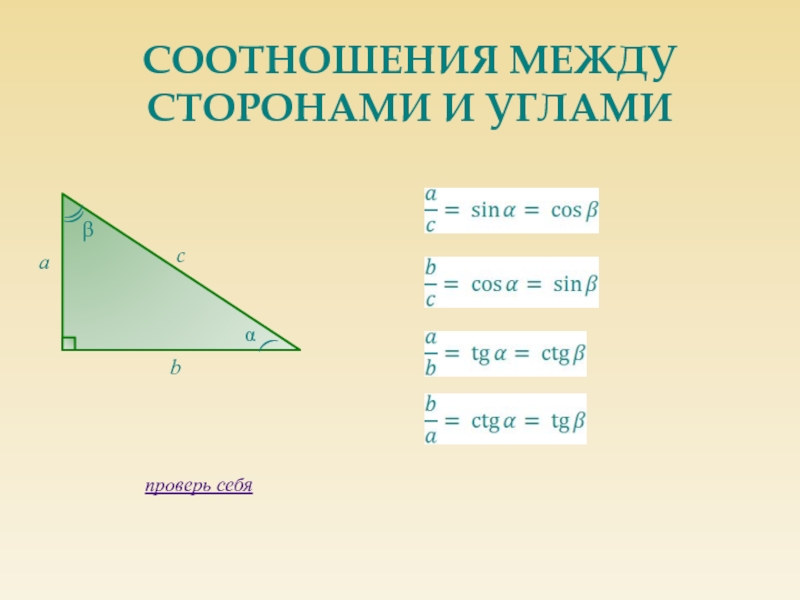
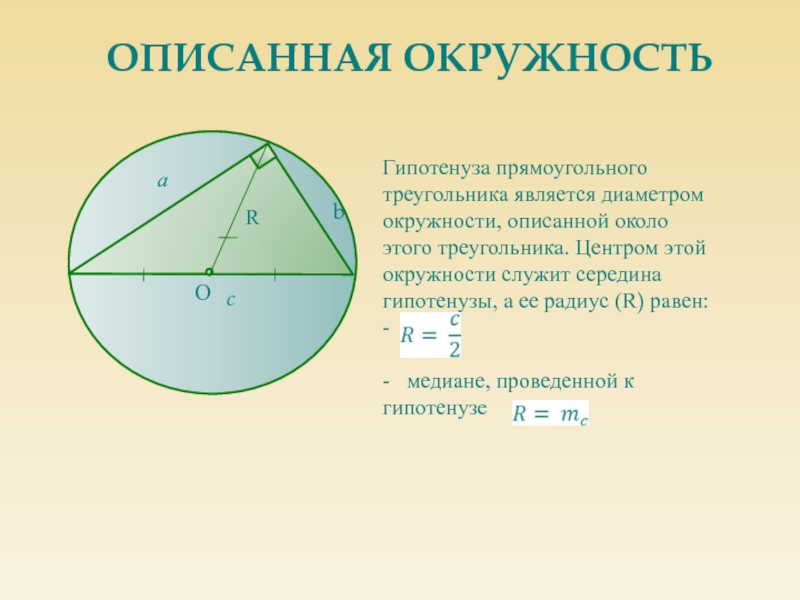
Стороны, прилежащие к прямому углу, называются катетами (АС, ВС).

Свойства
1. Сумма двух острых углов равна 900 .
2. Катет, лежащий против угла в 300 , равен половине гипотенузы.
3. Если катет равен половине гипотенузы, то угол, лежащий против этого катета, равен 300 .

Учитель математики МАОУ СОШ № 22
г. Тамбова Склярова Светлана Александровна

Прямоугольный треугольникТреугольник, у которого один угол прямой, называется прямоугольным.Сторона, лежащая против прямого угла, называется гипотенузой (АВ).Стороны, прилежащие

Слайд 2Признаки равенства
А
В
С
A1
B1
C1
По двум катетам.
По катету и гипотенузе.
По катету и

прилежащему острому углу.
По катету и противолежащему острому углу.
По гипотенузе и острому углу.

Признаки равенстваАВСA1B1 C1 По двум катетам.По катету и гипотенузе.По катету и прилежащему острому углу.По катету и противолежащему

Слайд 3Признаки подобия
А
В
С
A1
B1
C1
ΔABC ∞ Δ A1B1C1 ,

если
∠A = ∠A1

2.

3.

Слайд 4Теорема Пифагора
Сумма квадратов катетов равна квадрату гипотенузы:
Справедливо и обратное утверждение: если

для сторон
треугольника выполняется соотношение
то треугольник является прямоугольным, причем стороны a и b – его
катеты, а сторона с – гипотенуза.

a, b, c

Теорема ПифагораСумма квадратов катетов равна квадрату гипотенузы:Справедливо и обратное утверждение: если для сторон треугольника выполняется соотношение то

Слайд 5Соотношения между сторонами и углами
а
b
c
α
β
)
)
)
проверь себя

Слайд 6Свойства проекций катетов
a
b
c
h
Высота, опущенная на гипотенузу, является средним пропорциональным между проекциями

катетов на гипотенузу:

Высота выражается через стороны и проекции катетов:

Каждый катет является средним пропорциональным между гипотенузой и проекцией этого катета на гипотенузу:

Свойства проекций катетовabchВысота, опущенная на гипотенузу, является средним пропорциональным между проекциями катетов на гипотенузу:Высота выражается через стороны

Слайд 7Вписанная окружность
a
b
c
r
Радиус вписанной окружности
r, он равен:
Длина гипотенузы и полупериметр связаны с

радиусом вписанной окружности формулой: r + c = p

Вписанная окружностьabcrРадиус вписанной окружностиr, он равен:Длина гипотенузы и полупериметр связаны с радиусом вписанной окружности формулой: r

Слайд 8Описанная окружность
a
b
c
R
O
Гипотенуза прямоугольного треугольника является диаметром окружности, описанной около этого треугольника.

Центром этой окружности служит середина гипотенузы, а ее радиус (R) равен:
-

- медиане, проведенной к гипотенузе

Описанная окружностьabcROГипотенуза прямоугольного треугольника является диаметром окружности, описанной около этого треугольника. Центром этой окружности служит середина гипотенузы,

Слайд 9Площадь треугольника
а
b
c
α
β
)
)
)

Скачать презентацию

Презентация, доклад по теме прямоугольный треугольник для итогового повторения в 9 классе

Содержание

Слайд 1Прямоугольный треугольник
Треугольник, у которого один угол прямой, называется прямоугольным.
Сторона, лежащая против

Слайд 2Признаки равенства
А
В
С
A1
B1
C1
По двум катетам.
По катету и гипотенузе.
По катету и

Слайд 3Признаки подобия
А
В
С
A1
B1
C1
ΔABC ∞ Δ A1B1C1 ,

Слайд 4Теорема Пифагора
Сумма квадратов катетов равна квадрату гипотенузы:
Справедливо и обратное утверждение: если

Слайд 5Соотношения между сторонами и углами
а
b
c
α
β
)
)
)
проверь себя

Слайд 6Свойства проекций катетов
a
b
c
h
Высота, опущенная на гипотенузу, является средним пропорциональным между проекциями

Слайд 7Вписанная окружность
a
b
c
r
Радиус вписанной окружности
r, он равен:
Длина гипотенузы и полупериметр связаны с

Слайд 8Описанная окружность
a
b
c
R
O
Гипотенуза прямоугольного треугольника является диаметром окружности, описанной около этого треугольника.

Слайд 9Площадь треугольника
а
b
c
α
β
)
)
)

Что такое shareslide.ru?

Обратная связь

Презентация, доклад по теме прямоугольный треугольник для итогового повторения в 9 классе

Содержание

Слайд 1Прямоугольный треугольникТреугольник, у которого один угол прямой, называется прямоугольным.Сторона, лежащая против

Слайд 2Признаки равенстваАВСA1B1 C1 По двум катетам.По катету и гипотенузе.По катету и

Слайд 3Признаки подобияАВСA1B1 C1 ΔABC ∞ Δ A1B1C1 ,

Слайд 4Теорема ПифагораСумма квадратов катетов равна квадрату гипотенузы:Справедливо и обратное утверждение: если

Слайд 5Соотношения между сторонами и углами аbcαβ)))проверь себя

Слайд 6Свойства проекций катетовabchВысота, опущенная на гипотенузу, является средним пропорциональным между проекциями

Слайд 7Вписанная окружностьabcrРадиус вписанной окружностиr, он равен:Длина гипотенузы и полупериметр связаны с

Слайд 8Описанная окружностьabcROГипотенуза прямоугольного треугольника является диаметром окружности, описанной около этого треугольника.

Слайд 9Площадь треугольника аbcαβ)))

Похожие презентации

Что такое shareslide.ru?

Обратная связь

Слайд 1Прямоугольный треугольник
Треугольник, у которого один угол прямой, называется прямоугольным.
Сторона, лежащая против

Слайд 2Признаки равенства
А
В
С
A1
B1
C1
По двум катетам.
По катету и гипотенузе.
По катету и

Слайд 3Признаки подобия
А
В
С
A1
B1
C1
ΔABC ∞ Δ A1B1C1 ,

Слайд 4Теорема Пифагора
Сумма квадратов катетов равна квадрату гипотенузы:
Справедливо и обратное утверждение: если

Слайд 5Соотношения между сторонами и углами
а
b
c
α
β
)
)
)
проверь себя

Слайд 6Свойства проекций катетов
a
b
c
h
Высота, опущенная на гипотенузу, является средним пропорциональным между проекциями

Слайд 7Вписанная окружность
a
b
c
r
Радиус вписанной окружности
r, он равен:
Длина гипотенузы и полупериметр связаны с

Слайд 8Описанная окружность
a
b
c
R
O
Гипотенуза прямоугольного треугольника является диаметром окружности, описанной около этого треугольника.

Слайд 9Площадь треугольника
а
b
c
α
β
)
)
)