- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Пирамида (10 класс)
Содержание
- 1. Презентация по геометрии Пирамида (10 класс)
- 2. Пирамида — многогранник — многогранник, в основании которого лежит многоугольник, а
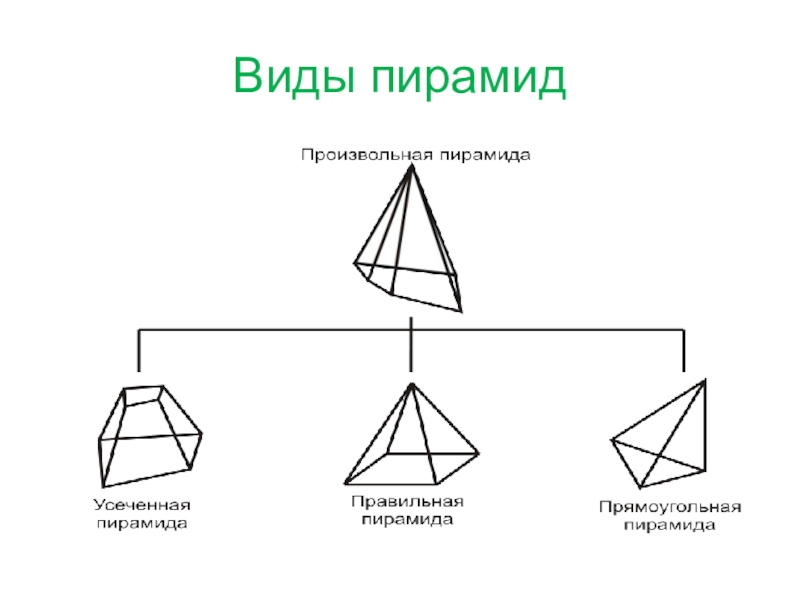
- 3. Виды пирамид
- 4. Правильная пирамида Определение. Пирамида называется правильной, если
- 5. Усеченная пирамида. Определение. Усеченной пирамидой является многогранник, заключенный меж
- 6. Формулы для нахождения площадей поверхности.
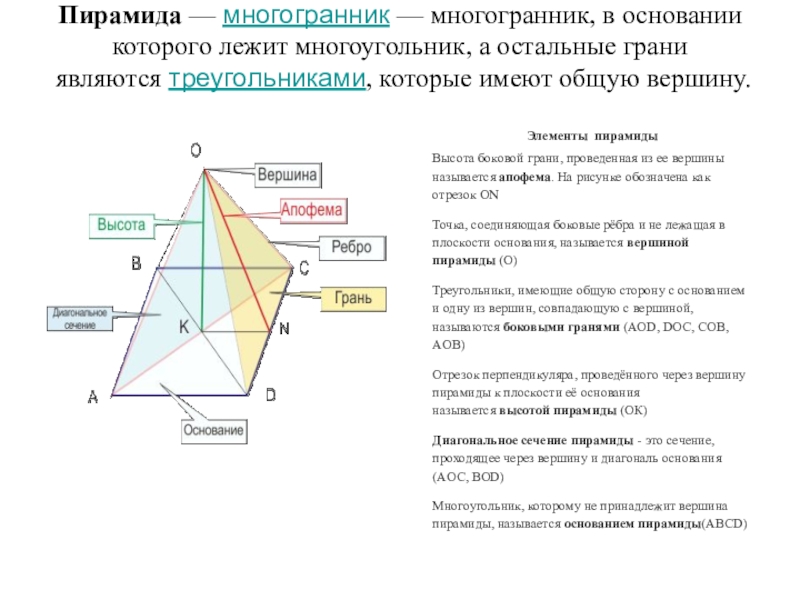
Слайд 2Пирамида — многогранник — многогранник, в основании которого лежит многоугольник, а остальные грани являются треугольниками, которые
Элементы пирамиды
Высота боковой грани, проведенная из ее вершины называется апофема. На рисунке обозначена как отрезок ON
Точка, соединяющая боковые рёбра и не лежащая в плоскости основания, называется вершиной пирамиды (О)
Треугольники, имеющие общую сторону с основанием и одну из вершин, совпадающую с вершиной, называются боковыми гранями (AOD, DOC, COB, AOB)
Отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания называется высотой пирамиды (ОК)
Диагональное сечение пирамиды - это сечение, проходящее через вершину и диагональ основания (AOC, BOD)
Многоугольник, которому не принадлежит вершина пирамиды, называется основанием пирамиды(ABCD)
Слайд 4Правильная пирамида Определение. Пирамида называется правильной, если ее основание – правильный многоугольник,
Свойства правильной пирамиды
боковые ребра равны между собой
апофемы равны
боковые грани равны между собой (при этом, соответственно, равны их площади, боковые стороны и основания), то есть они являются равными треугольниками
все боковые грани являются равными равнобедренными треугольниками
в любую правильную пирамиду можно как вписать, так и описать около неё сферу
если центры вписанной и описанной сферы совпадают, то сумма плоских углов при вершине пирамиды равна π, а каждый из них соответственно π/n, где n — количество сторон многоугольника основания
площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему
около основания правильной пирамиды можно описать окружность
все боковые грани образуют с плоскостью основания правильной пирамиды равные углы
все высоты боковых граней равны между собой
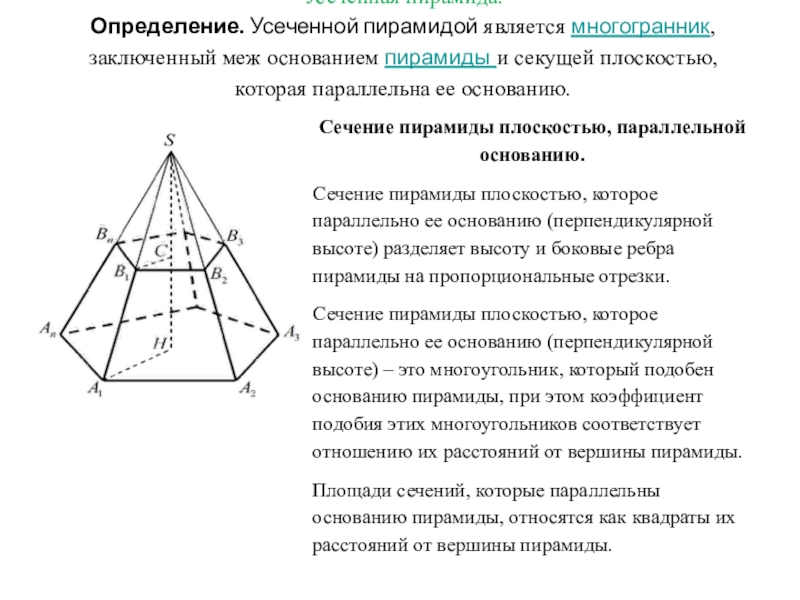
Слайд 5Усеченная пирамида. Определение. Усеченной пирамидой является многогранник, заключенный меж основанием пирамиды и секущей плоскостью, которая параллельна
Сечение пирамиды плоскостью, параллельной основанию.
Сечение пирамиды плоскостью, которое параллельно ее основанию (перпендикулярной высоте) разделяет высоту и боковые ребра пирамиды на пропорциональные отрезки.
Сечение пирамиды плоскостью, которое параллельно ее основанию (перпендикулярной высоте) – это многоугольник, который подобен основанию пирамиды, при этом коэффициент подобия этих многоугольников соответствует отношению их расстояний от вершины пирамиды.
Площади сечений, которые параллельны основанию пирамиды, относятся как квадраты их расстояний от вершины пирамиды.