- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Взаимное расположение прямой и окружности (9 класс)
Содержание
- 1. Презентация по геометрии на тему Взаимное расположение прямой и окружности (9 класс)
- 2. Цель урока:1.Разобрать возможные случаи, взаимного расположения прямой
- 3. Дано:Окружность с центром в точке О радиуса
- 4. Возможны три случая:1) s
- 5. Возможны три случая:2) s=rЕсли расстояние от центра
- 6. Возможны три случая:3) s>rЕсли расстояние от центра
- 7. Выясните взаимное расположение прямой и окружности, если:r
- 8. Решаем вместеЗадача 1Написать уравнение окружности в общем
- 9. Слайд 9
- 10. Решаем вместеЗадача 3
- 11. Если необходимо найти координаты точек пересечения,
- 12. Сколько общих точек могут иметь прямая и
- 13. Самостоятельная работаВариант 1Определите количество общих точек прямой
Слайд 2Цель урока:
1.Разобрать возможные случаи, взаимного расположения прямой и окружности.
2.Разобрать типовые задачи
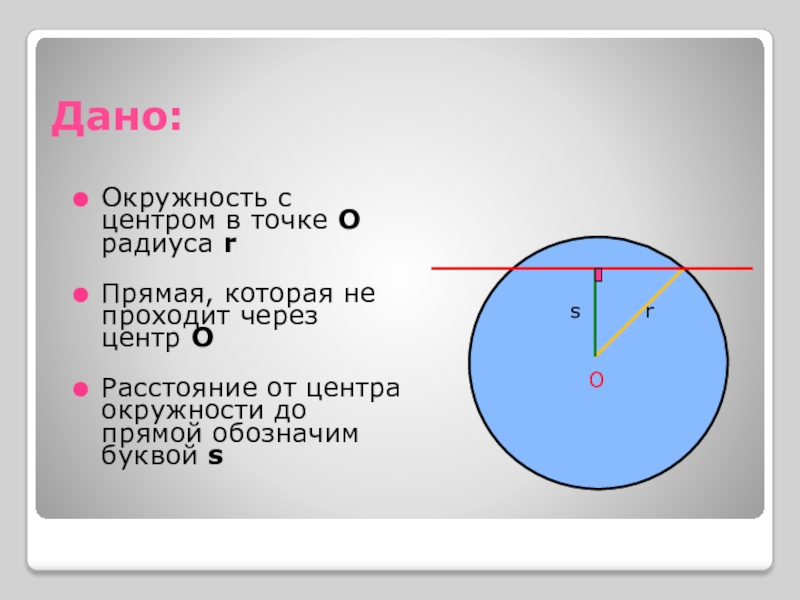
Слайд 3Дано:
Окружность с центром в точке О радиуса r
Прямая, которая не проходит
Расстояние от центра окружности до прямой обозначим буквой s
O
r
s
Слайд 4Возможны три случая:
1) s
O
s А В Прямая АВ называется секущей по отношению к окружности.
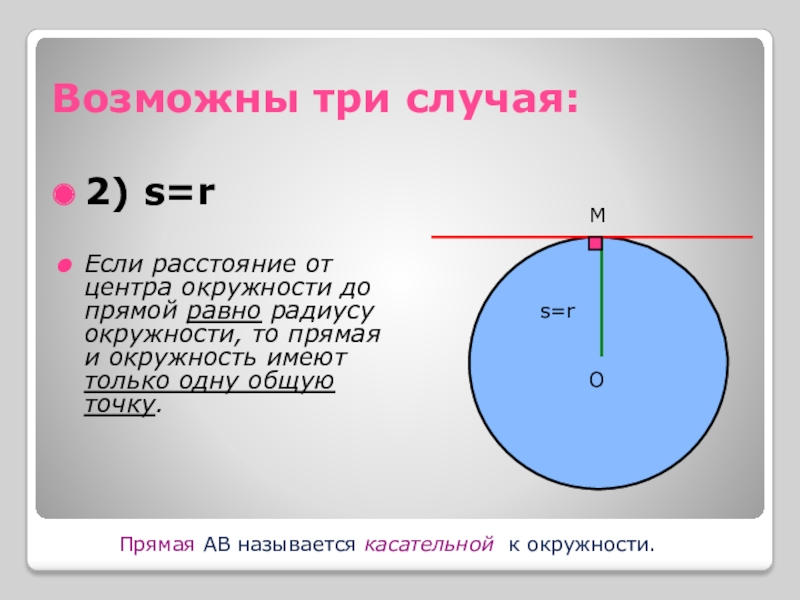
Слайд 5Возможны три случая:
2) s=r
Если расстояние от центра окружности до прямой равно
O
s=r
M
Прямая АВ называется касательной к окружности.
Слайд 6Возможны три случая:
3) s>r
Если расстояние от центра окружности до прямой больше
O
s>r
r
Прямая АВ не пересекает окружность.
Слайд 7Выясните взаимное расположение прямой и окружности, если:
r = 15 см, s
r = 6 см, s = 5,2 см
r = 3,2 м, s = 4,7 м
r = 7 см, s = 0,5 дм
r = 4 см, s = 40 мм
прямая – секущая
прямая – секущая
общих точек нет
прямая – секущая
прямая - касательная
Слайд 8Решаем вместе
Задача 1
Написать уравнение окружности в общем виде с центром в
Решение
Уравнение окружности необходимо записать в виде:
(х-2)²+(у+7)²=R².
Найдем радиус.
Так как окружность касается оси Ох, то точка касания имеет координаты (2;0).
Так как касательная расположена
перпендикулярно к окружности, то R=7.
Получили уравнение (х-2)²+(у+7)²=49.
Ответ: (х-2)²+(у+7)²=49
O
У
х
2
•
•
•
-7
R
Слайд 9
Задача 2
Найти координаты точек пересечения окружности х2+у2-8х-8у+7=0 с осью Ох.
Решение
Ось Ох задается уравнением : У=0.
Для нахождения точек пересечения решим систему уравнений:
Во второе уравнение подставим у=0, получим систему:
Решим второе уравнение относительно переменной Х:
Х1+Х2=8, Х1=1
Х1*Х2=7, Х2 =7.
Ответ: (1;0), (7;0).
Слайд 10 Решаем вместе
Задача 3
Пересекает ли прямая 2х+у=7
Решение
Для решения задачи составим систему уравнений прямой и окружности:
Решим второе уравнение:
Х2+2х+1+4-8х+4х2-13=0,
5х2-6х-8=0,
Д =36+4*5*8=36+160=196 > 0.
Так как Д> 0, то данное уравнение, а значит и система уравнений, имеют два решения
Следовательно, прямая и окружность пересекаются.
Ответ: прямая и окружность пересекаются.
Слайд 11 Если необходимо найти координаты точек пересечения, то находим корни уравнения:
замечание
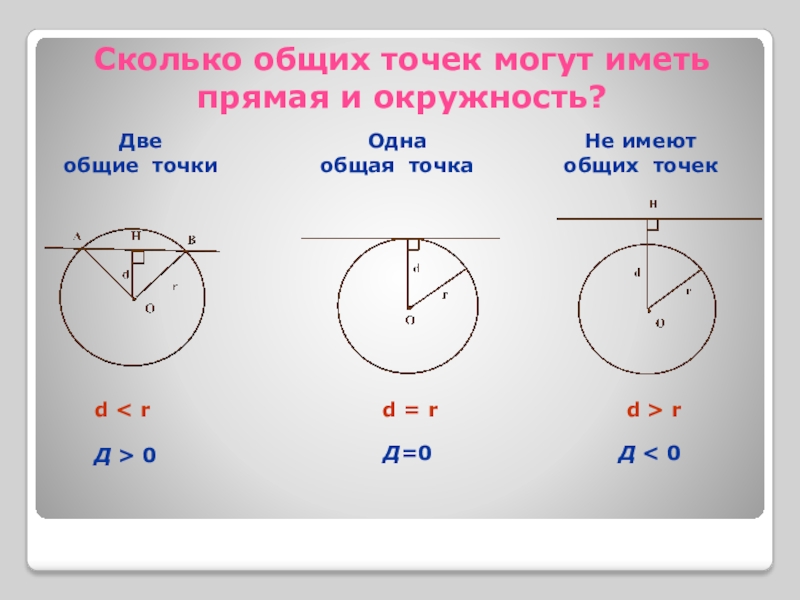
Слайд 12Сколько общих точек могут иметь прямая и окружность?
Две
Одна общая точка
Не имеют общих точек
d < r
d = r
d > r
Д > 0
Д < 0
Д=0
Слайд 13Самостоятельная работа
Вариант 1
Определите количество общих точек прямой у=х и окружности х²+у²=3.
Найдите
Вариант 2
Определите количество общих точек прямой у=х и окружности х²+у²=4.
Найдите координаты точек пересечения прямой у-х=3 и окружности (х+5)²+у²=2
⃰⃰ При каких значениях а прямая х-у=а и окружность х²+у²=9 не пересекаются.
Дом. задание: выполнить вариант соседа,
повторить решение типовых задач.