- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Простейшие фигуры и аксиомы планиметрии
Содержание
- 1. Презентация Простейшие фигуры и аксиомы планиметрии
- 2. Точка – неопределяемое понятие. Представление о точке
- 3. Прямая – неопределяемое понятие. Представление о прямой
- 4. Плоскость – неопределяемое понятие. Представление о плоскости
- 5. Луч( полупрямая )- часть прямой, состоящая из
- 6. Аксиомы планиметрии
- 7. Аксиомы принадлежности точек и прямых на плоскости1.
- 8. Аксиомы взаимного размещения точек на прямой и
- 9. Аксиомы измерения отрезков и угловКаждый отрезок имеет
- 10. Аксиомы отложения отрезков и углов1. На любой
- 11. 3. Каким бы ни был треугольник, существует
- 12. Спасибо за внимание!
Слайд 2
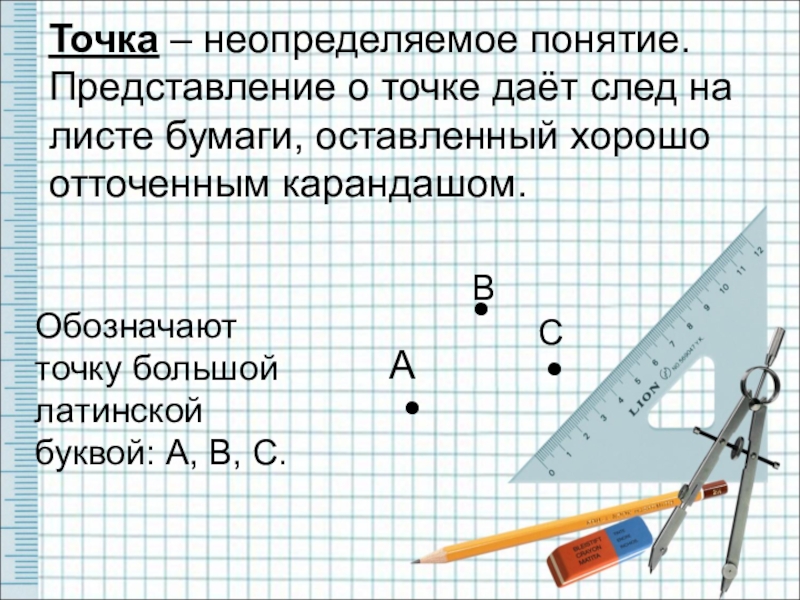
Точка – неопределяемое понятие. Представление о точке даёт след на листе
Обозначают точку большой латинской буквой: А, В, С.
•
•
•
А
В
С
Слайд 3Прямая – неопределяемое понятие. Представление о прямой дают: туго натянутая нитка,
Обозначают прямую маленькой латинской буквой: а, b…или двумя большими латинскими буквами: АС, ВС.
•
•
А
В
С
а
b
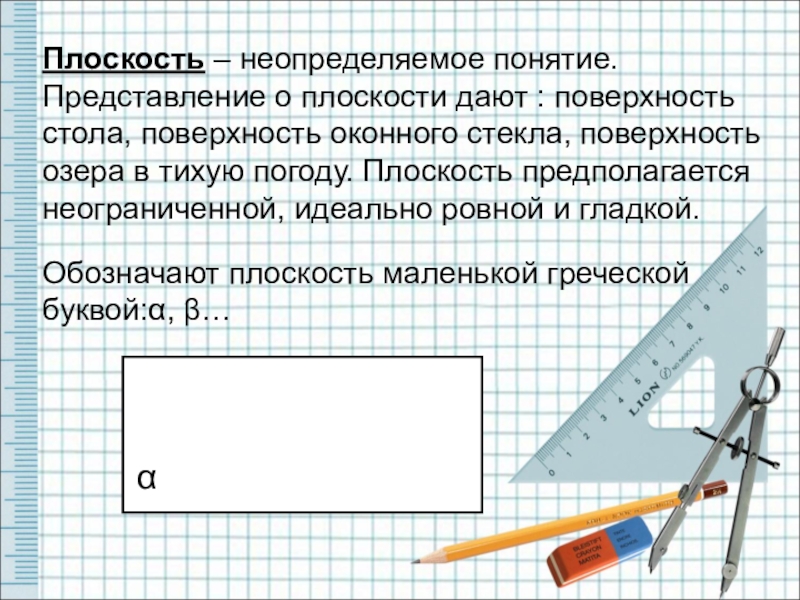
Слайд 4Плоскость – неопределяемое понятие. Представление о плоскости дают : поверхность стола,
Обозначают плоскость маленькой греческой буквой:α, β…
α
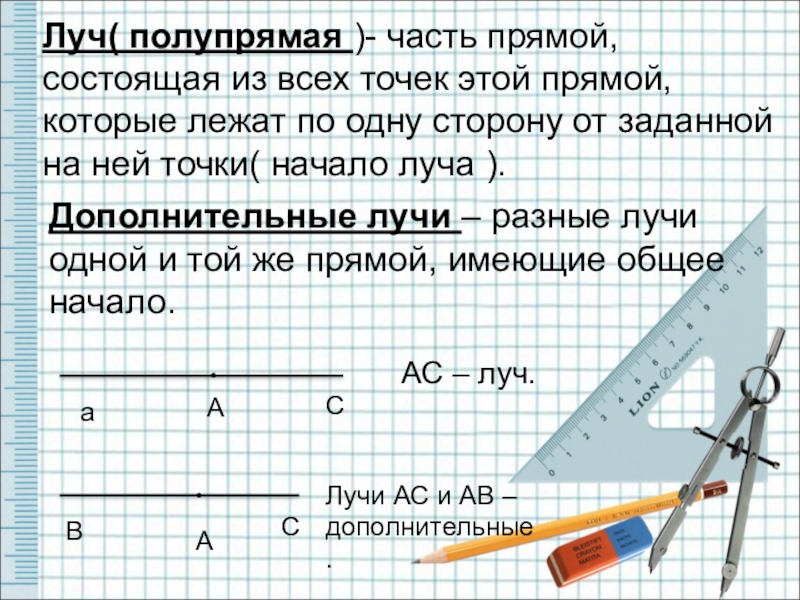
Слайд 5Луч( полупрямая )- часть прямой, состоящая из всех точек этой прямой,
Дополнительные лучи – разные лучи одной и той же прямой, имеющие общее начало.
•
А
а
С
АС – луч.
•
А
В
С
Лучи АС и АВ – дополнительные.
Слайд 7
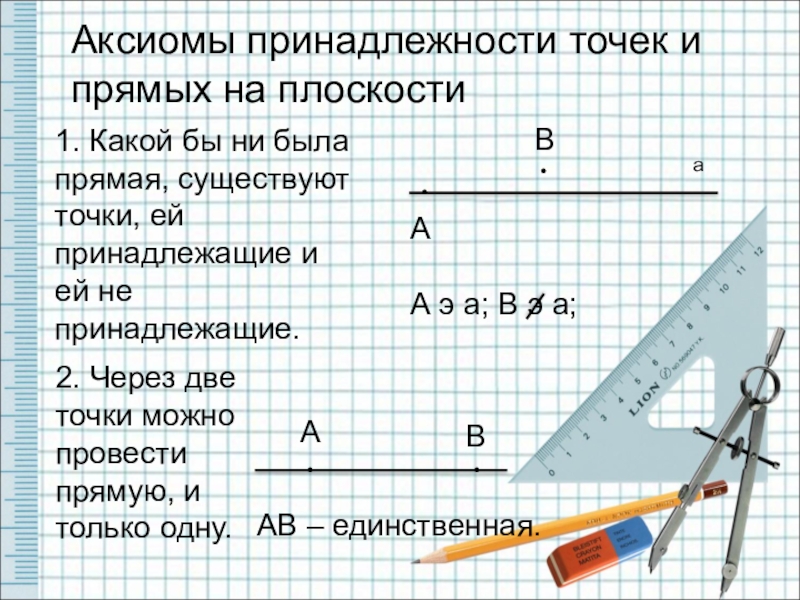
Аксиомы принадлежности точек и прямых на плоскости
1. Какой бы ни была
2. Через две точки можно провести прямую, и только одну.
А
В
•
•
а
А э а; В э а;
А
В
•
•
АВ – единственная.
Слайд 8
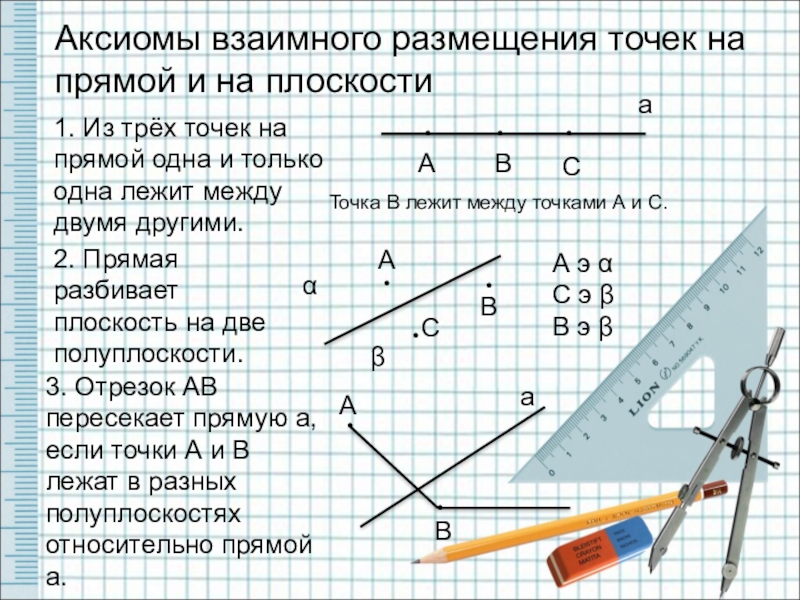
Аксиомы взаимного размещения точек на прямой и на плоскости
1. Из
2. Прямая разбивает плоскость на две полуплоскости.
3. Отрезок АВ пересекает прямую а, если точки А и В лежат в разных полуплоскостях относительно прямой а.
А
В
С
•
•
•
а
Точка В лежит между точками А и С.
А
В
а
•
•
А
В
С
α
β
•
•
•
А э α
С э β
В э β
Слайд 9
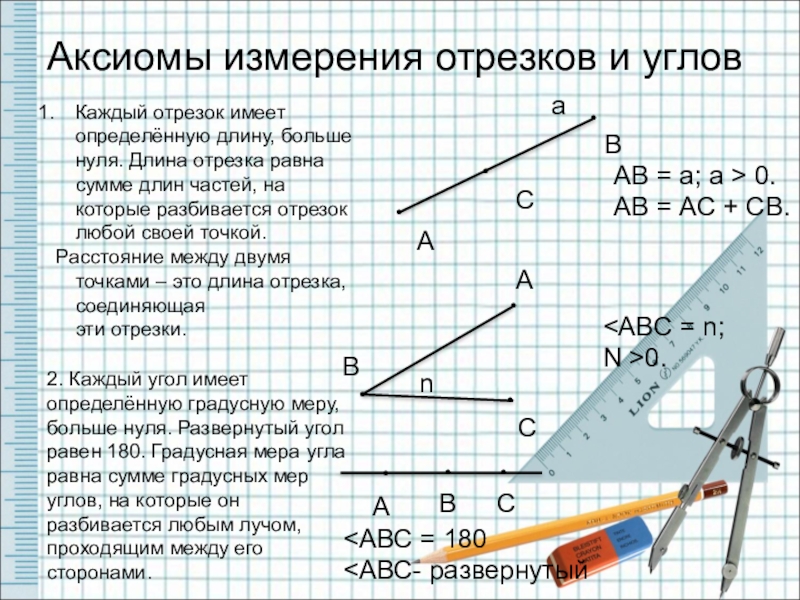
Аксиомы измерения отрезков и углов
Каждый отрезок имеет определённую длину, больше нуля.
Расстояние между двумя точками – это длина отрезка, соединяющая эти отрезки.
2. Каждый угол имеет определённую градусную меру, больше нуля. Развернутый угол равен 180. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
А
С
В
а
АВ = а; а > 0.
АВ = АС + СВ.
•
•
•
В
А
С
<АВС = n;
N >0.
n
•
•
•
•
•
•
А
В
С
<АВС = 180
<АВС- развернутый
Слайд 10
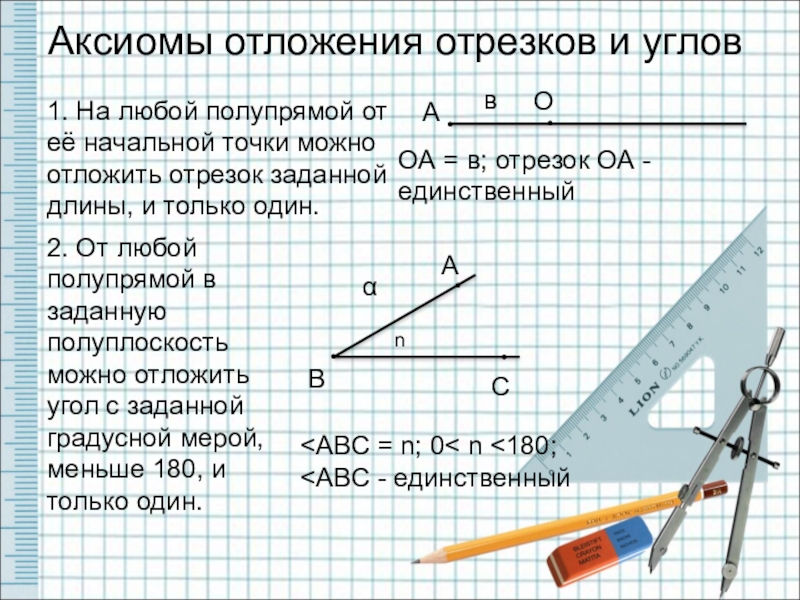
Аксиомы отложения отрезков и углов
1. На любой полупрямой от её начальной
2. От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньше 180, и только один.
ОА = в; отрезок ОА - единственный
А
О
в
•
•
В
А
С
<АВС = n; 0< n <180;
<АВС - единственный
•
•
•
n
α
Слайд 11
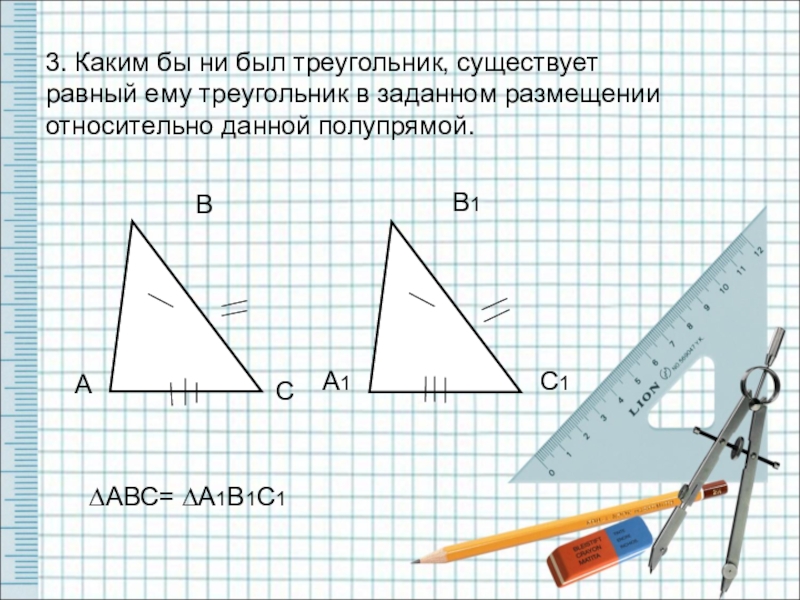
3. Каким бы ни был треугольник, существует равный ему треугольник в
А
В
С
А1
В1
С1
∆АВС= ∆А1В1С1