Урок 1
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Решение задач на различные комбинации тел 11 класс
Содержание
- 1. Презентация по геометрии Решение задач на различные комбинации тел 11 класс
- 2. Самостоятельная работа
- 3. Повторение: Какой многоугольник называется вписанным в окружность?
- 4. Повторение: Каким свойством обладает четырехугольник, который можно
- 5. Многогранник называется описанным около сферы, если сфера
- 6. Многогранник называется вписанным в сферу, если все
- 7. В любую треугольную пирамиду можно вписать
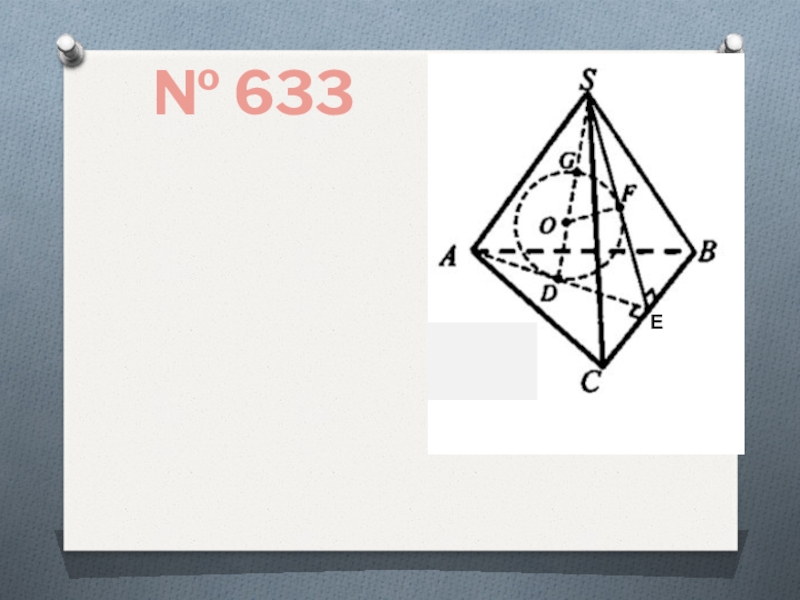
- 8. № 633 Е
- 9. Около любой треугольной пирамиды можно описать
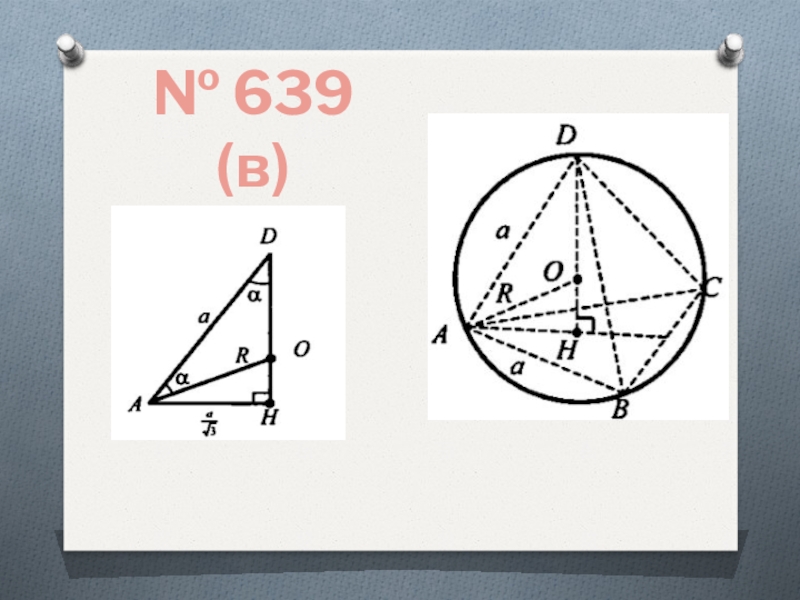
- 10. № 639 (в)Е
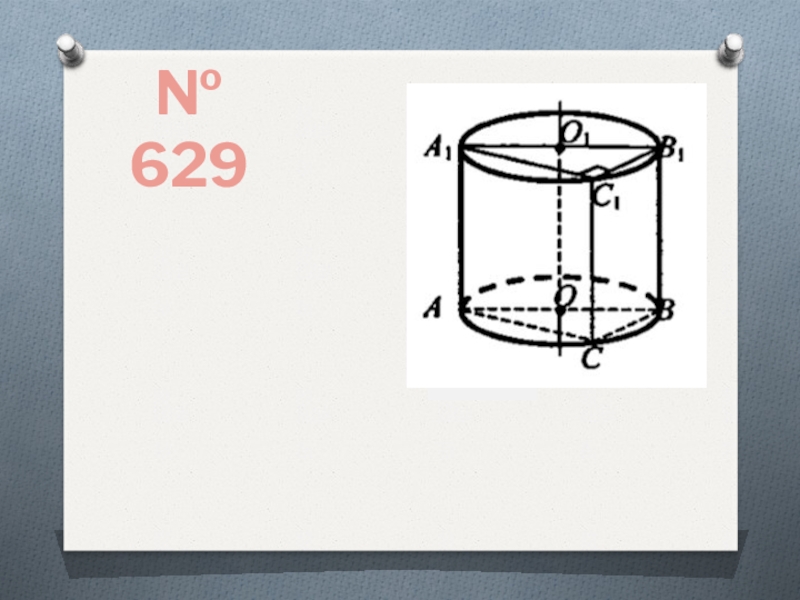
- 11. № 629
- 12. Домашнее задание:П.69, п.70№ 635, №637Дополнительная задача:Вычислите площадь
Самостоятельная работа
Слайд 1Решение задач
на
различные комбинации тел
Учитель математики
ГБОУ Школа № 1592
Крайнюк
А.Л.
Слайд 3Повторение:
Какой многоугольник называется вписанным в окружность?
Всякий ли треугольник можно
вписать в окружность?
Где находится центр окружности, описанной около треугольника?
Как найти радиус описанной вокруг треугольника окружности?
Всякий ли четырехугольник можно вписать в окружность?
Где находится центр окружности, описанной около треугольника?
Как найти радиус описанной вокруг треугольника окружности?
Всякий ли четырехугольник можно вписать в окружность?
Слайд 4Повторение:
Каким свойством обладает четырехугольник, который можно вписать в окружность?
Какой многоугольник
называется описанным около окружности?
Где находится центр окружности, вписанной в треугольник?
Как найти радиус описанной вокруг треугольника окружности?
Каким свойством обладает четырехугольник, в который можно вписать окружность?
Где находится центр окружности, вписанной в треугольник?
Как найти радиус описанной вокруг треугольника окружности?
Каким свойством обладает четырехугольник, в который можно вписать окружность?
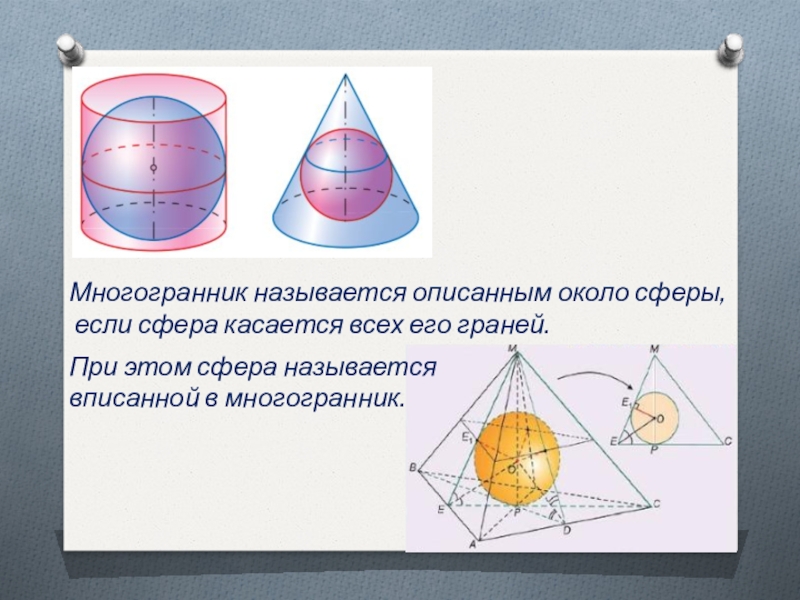
Слайд 5Многогранник называется описанным около сферы,
если сфера касается всех его граней.
При
этом сфера называется
вписанной в многогранник.
вписанной в многогранник.
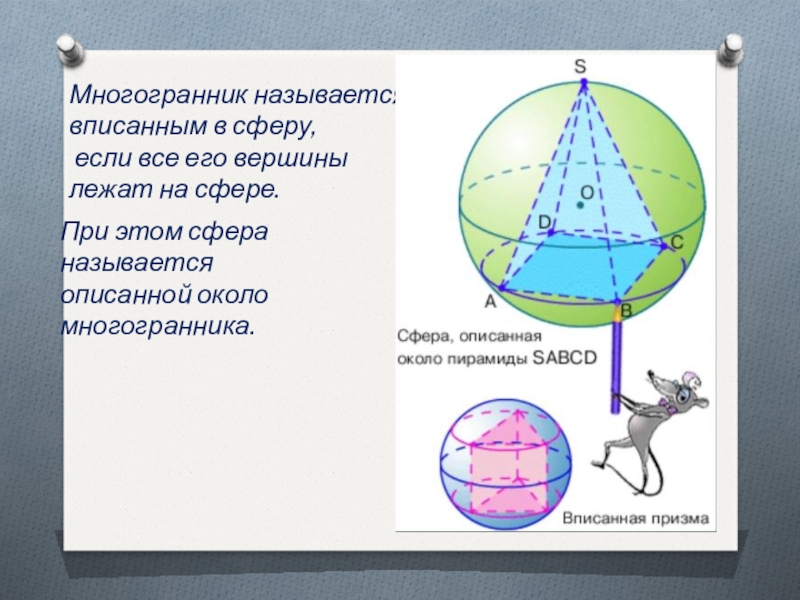
Слайд 6Многогранник называется вписанным в сферу,
если все его вершины лежат на
сфере.
При этом сфера называется описанной около
многогранника.
Слайд 7 В любую треугольную пирамиду можно вписать шар;
В пирамиду, в
основание которой можно вписать окружность, центр которой служит основанием высоты пирамиды, можно вписать шар;
В любую правильную пирамиду можно вписать шар;
Центр шара, вписанного в пирамиду, есть точка пересечения высоты пирамиды с биссектрисой угла, образованного апофемой и ее проекцией на основание;
Центр шара, вписанную в правильную пирамиду, лежит на высоте этой пирамиды.
В любую правильную пирамиду можно вписать шар;
Центр шара, вписанного в пирамиду, есть точка пересечения высоты пирамиды с биссектрисой угла, образованного апофемой и ее проекцией на основание;
Центр шара, вписанную в правильную пирамиду, лежит на высоте этой пирамиды.
Комбинация сферы и пирамиды
Слайд 9 Около любой треугольной пирамиды можно описать шар;
Если около основания
пирамиды можно описать окружность, то около пирамиды можно описать шар;
Вокруг любой правильной пирамиды можно описать шар;
Центр шара, описанного вокруг пирамиды, есть точка пересечения прямой, перпендикулярной основанию пирамиды, проходящей через центр описанной около основания окружности и плоскости, перпендикулярной любому боковому ребру, проведенной через середину этого ребра.
Вокруг любой правильной пирамиды можно описать шар;
Центр шара, описанного вокруг пирамиды, есть точка пересечения прямой, перпендикулярной основанию пирамиды, проходящей через центр описанной около основания окружности и плоскости, перпендикулярной любому боковому ребру, проведенной через середину этого ребра.
Комбинация сферы и пирамиды
Слайд 12Домашнее задание:
П.69, п.70
№ 635,
№637
Дополнительная задача:
Вычислите площадь поверхности шара, вписанного в
треугольную пирамиду, все ребра которой равны a.