Чему бы ты ни учился, ты учишься для себя.
(Петроний- сатирик Древней Греции)
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Решение задач на признаки подобия треугольников
Содержание
- 1. Презентация по геометрии Решение задач на признаки подобия треугольников
- 2. Приветствую вас на уроке геометрии в 8 классе Уроки №48-4912.01.2017 г.
- 3. Успешного усвоения материала Интересные
- 4. Отчёт по выполнению ДР в группе
- 5. Вопросы по ДР.
- 6. Экспресс-опрос по теории
- 7. 2. Отрезки АВ и CD называются
- 8. 4. Число k, равное отношению сходственных
- 9. 5. Отношение площадей двух подобных
- 10. 7. Биссектриса треугольника делит противоположную сторону
- 11. 9. Если два угла одного треугольника
- 12. 11. Если три стороны одного треугольника
- 13. 13. Треугольники АВС и KDN подобныНазовитепропорциональные стороны. 2) Назовите равные углы.
- 14. 14. Все круги между собой …
- 15. 17. Если сторона первого квадрата в
- 16. Оцените ДР
- 17. КРРешение задач на признаки подобия §1,2,пп.56-6112.01.2017г.
- 18. Закрепить теоретические знания по теме. Формировать навыки
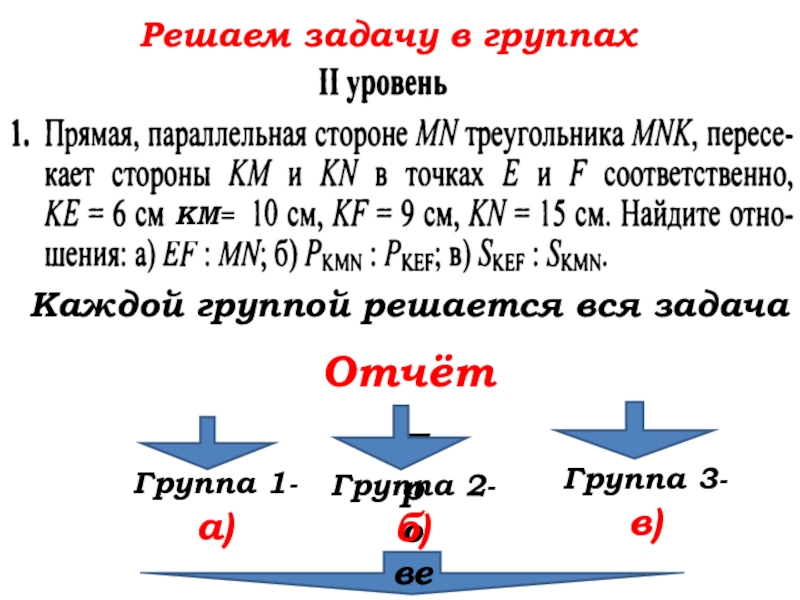
- 19. Решаем задачи в группах
- 20. Проверка Треугольники не являются подобными Решение:
- 21. Решаем задачи в группах
- 22. Проверка Треугольники являются подобными по 1 признаку Решение:
- 23. Решаем задачи в группах
- 24. Проверка Решение:Так как
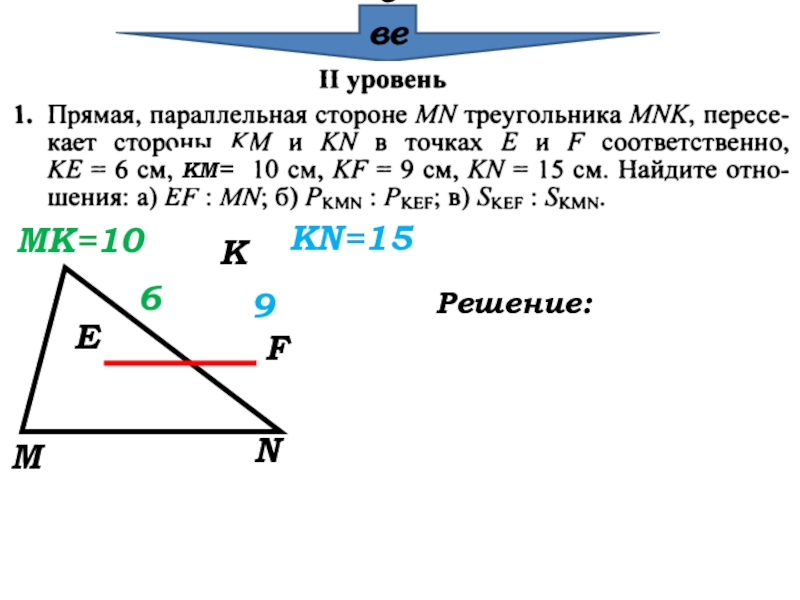
- 25. Решаем задачу в группах
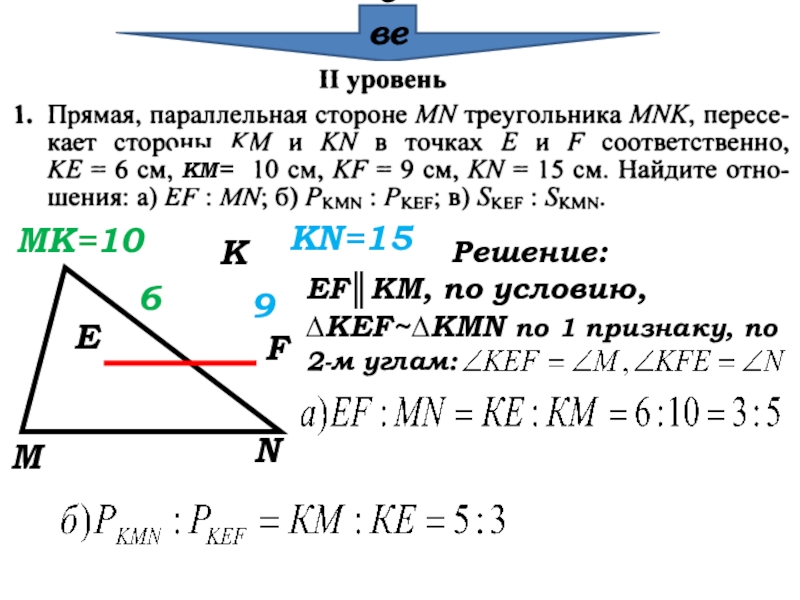
- 26. Проверка КМ=МКNEF69MK=10KN=15Решение:
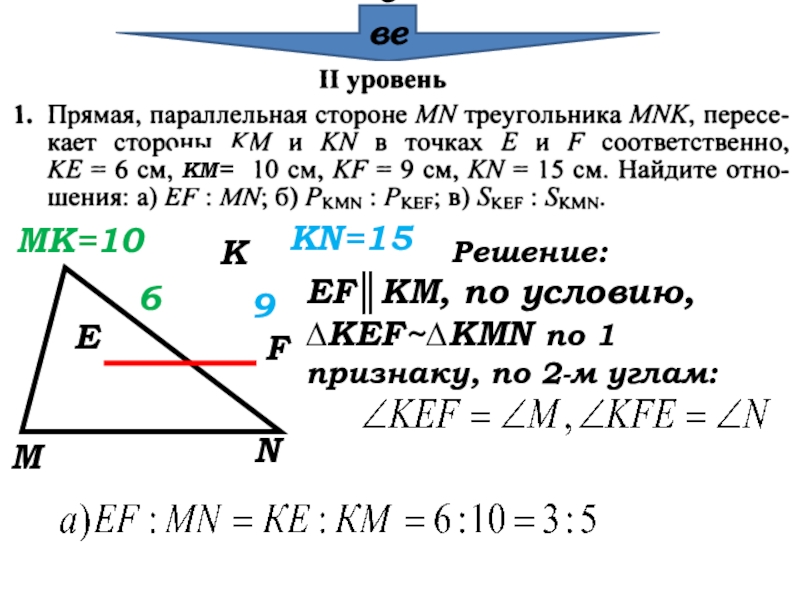
- 27. Проверка КМ=МКNEF69MK=10KN=15Решение:EF║KM, по условию,∆KEF~∆KMN по 1
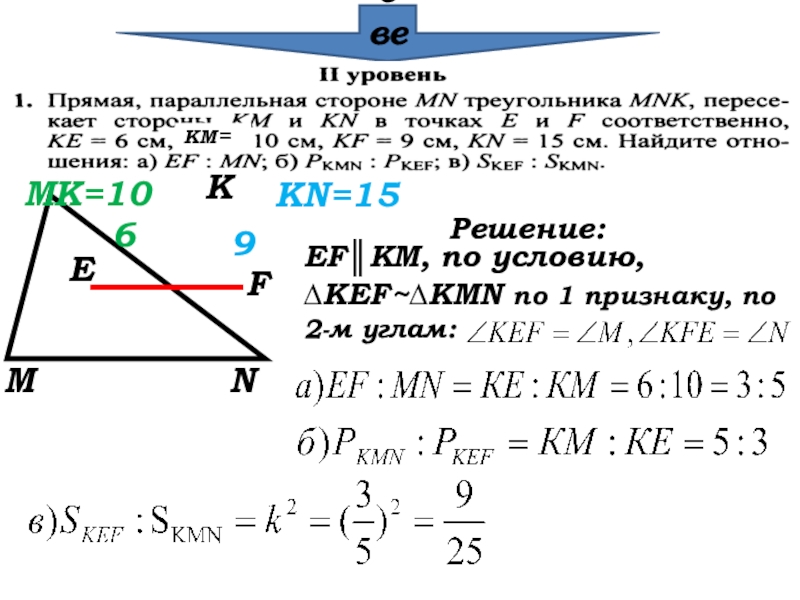
- 28. Проверка КМ=МКNEF69MK=10KN=15Решение:EF║KM, по условию,∆KEF~∆KMN по 1
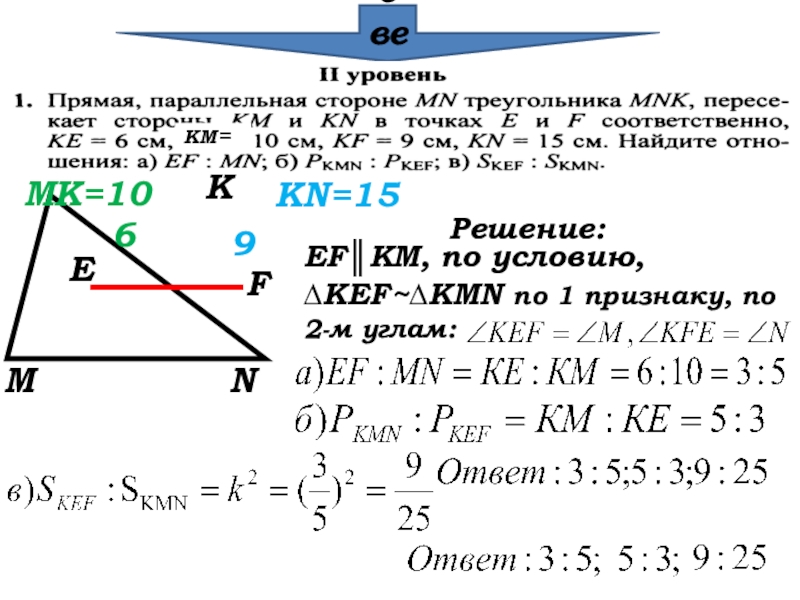
- 29. Проверка КМ=МКNEF69MK=10KN=15Решение:EF║KM, по условию,∆KEF~∆KMN по 1
- 30. Проверка КМ=МКNEF69MK=10KN=15Решение:EF║KM, по условию,∆KEF~∆KMN по 1
- 31. Решаем задачу вместе
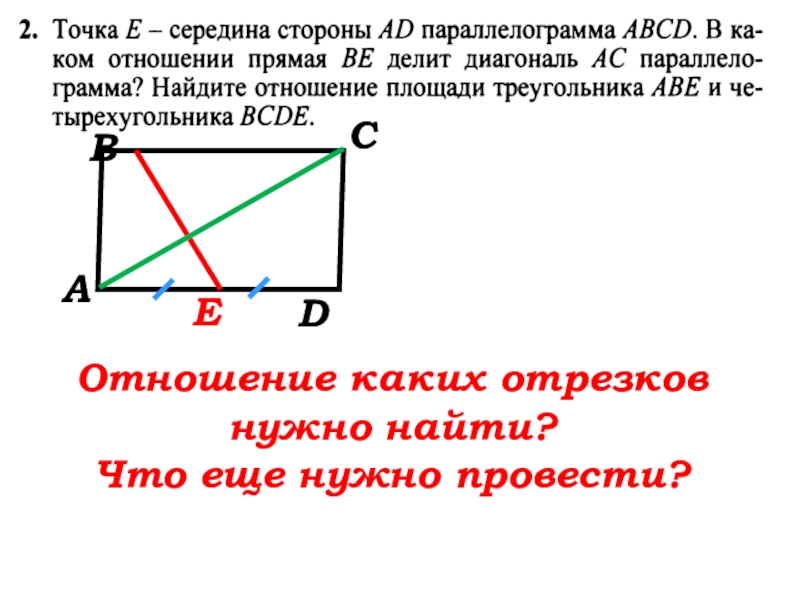
- 32. АВСDEОтношение каких отрезков нужно найти?Что еще нужно провести?
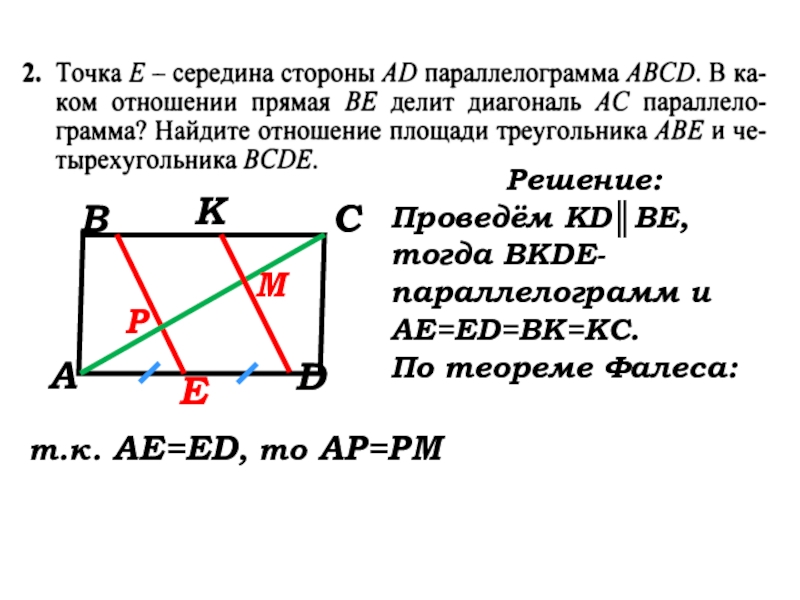
- 33. АВСDEKРМ Решение:Проведём KD║BE, тогда
- 34. АВСDEKРМ Решение:Проведём KD║BE, тогда КDEB-параллелограмм и ED=BK=KC.
- 35. АВСDEKРМ
- 36. АВСDEKРМ
- 37. АВСDEKРМ
- 38. АВСDEKРМ
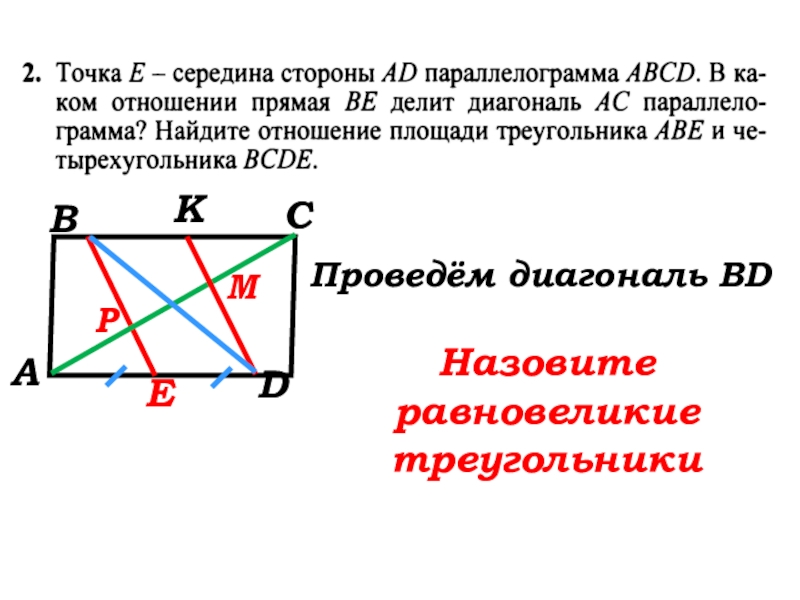
- 39. АВСDEKРМ Проведём диагональ BDНазовите равновеликие треугольники
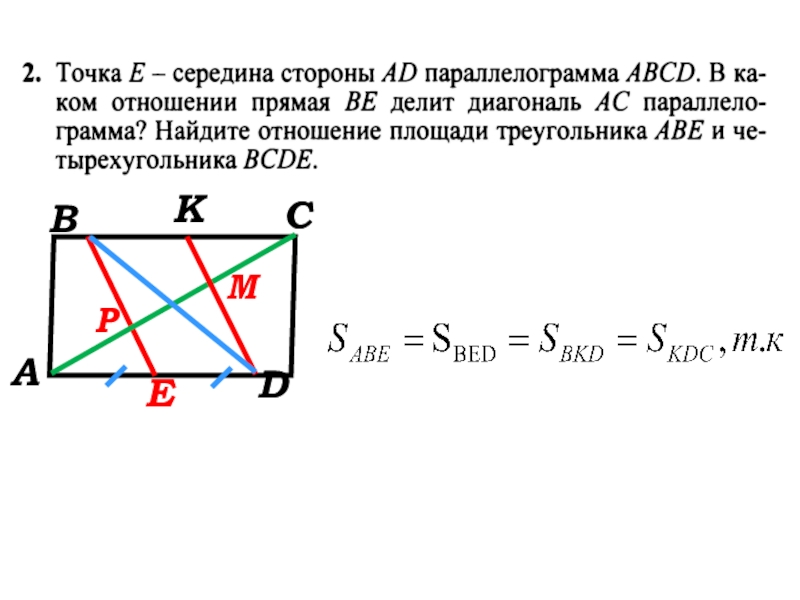
- 40. АВСDEKРМ
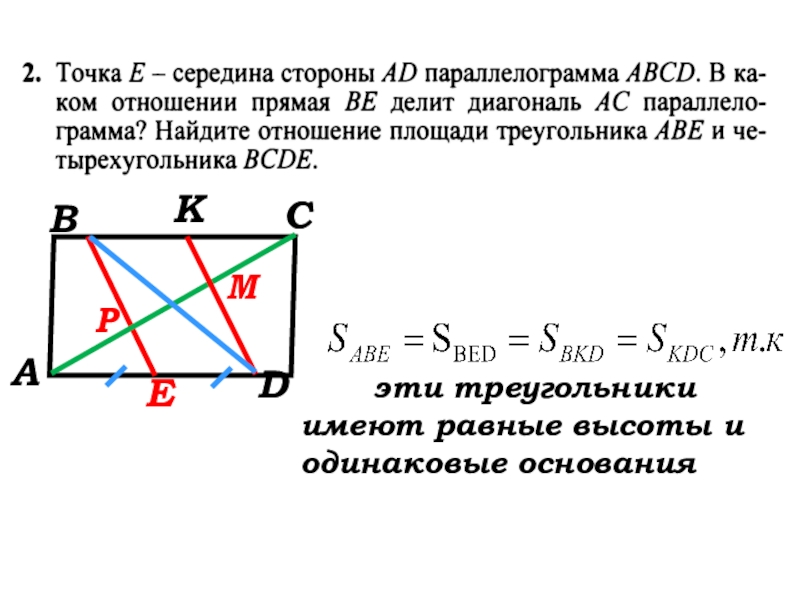
- 41. АВСDEKРМ эти треугольники имеют равные высоты и одинаковые основания
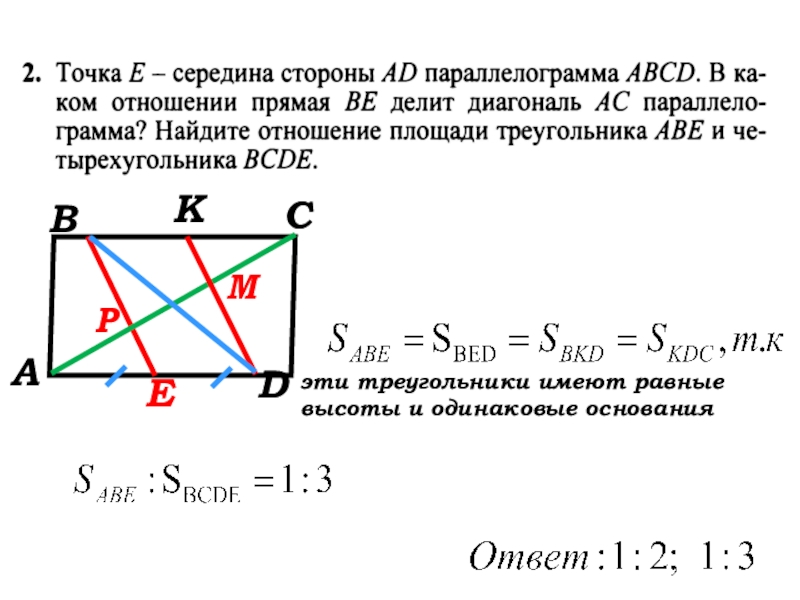
- 42. АВСDEKРМэти треугольники имеют равные высоты и одинаковые основания
- 43. Решаем задачу вместе Прочитайте задачу, выполните чертеж без обозначений
- 44. Решаем задачи вместе Что не построено на чертеже?Что нужно провести, чтобы указать расстояния?
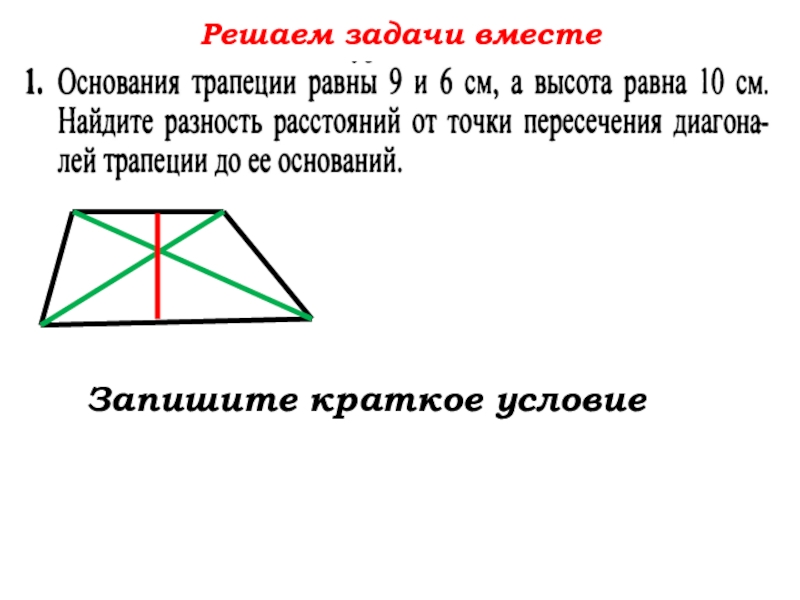
- 45. Решаем задачи вместе Запишите краткое условие
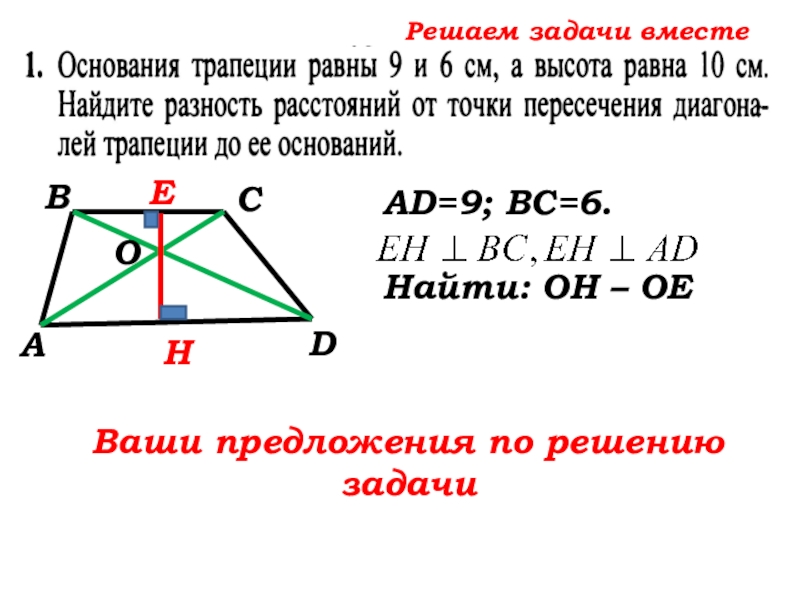
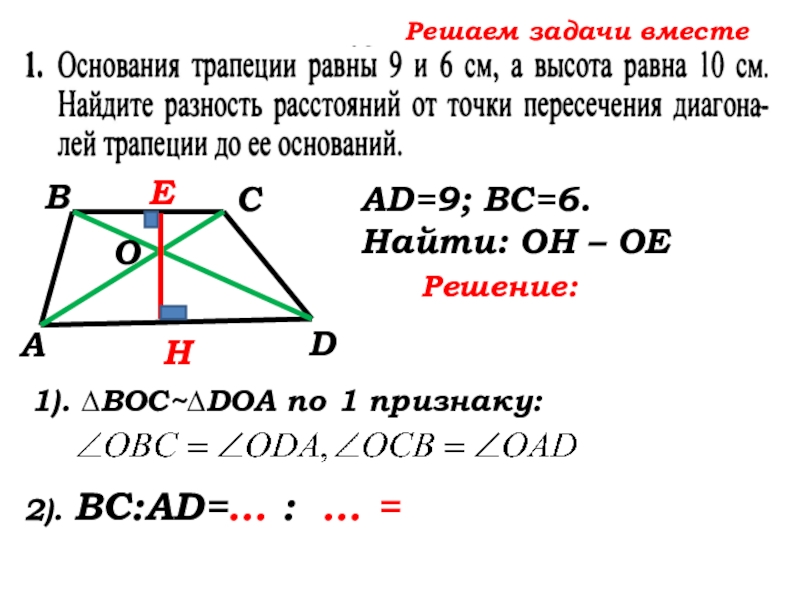
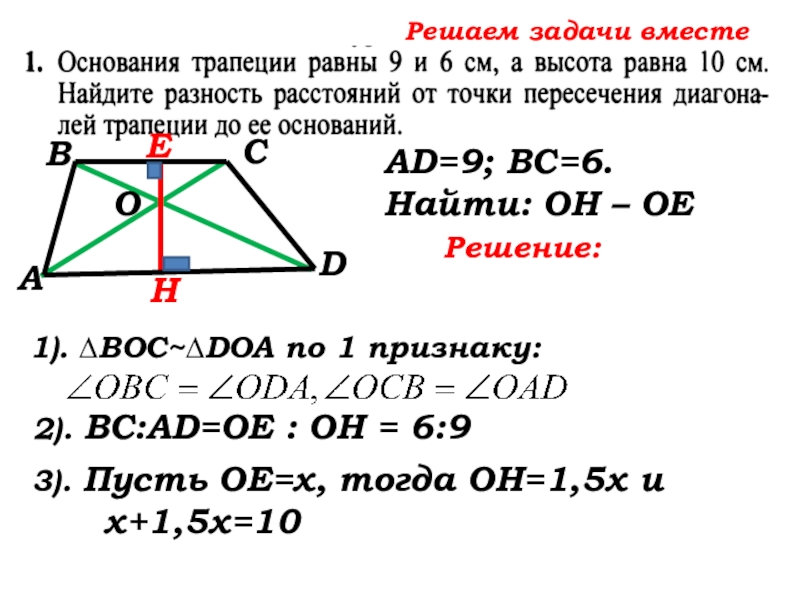
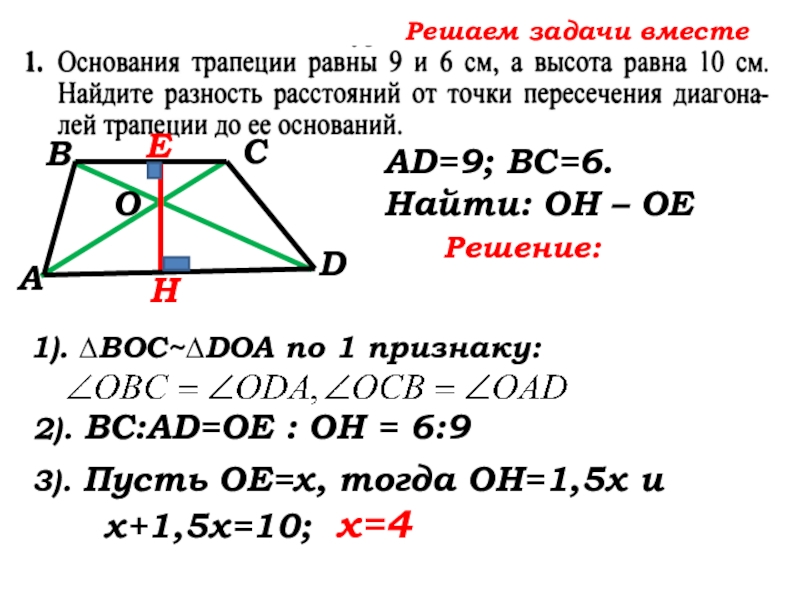
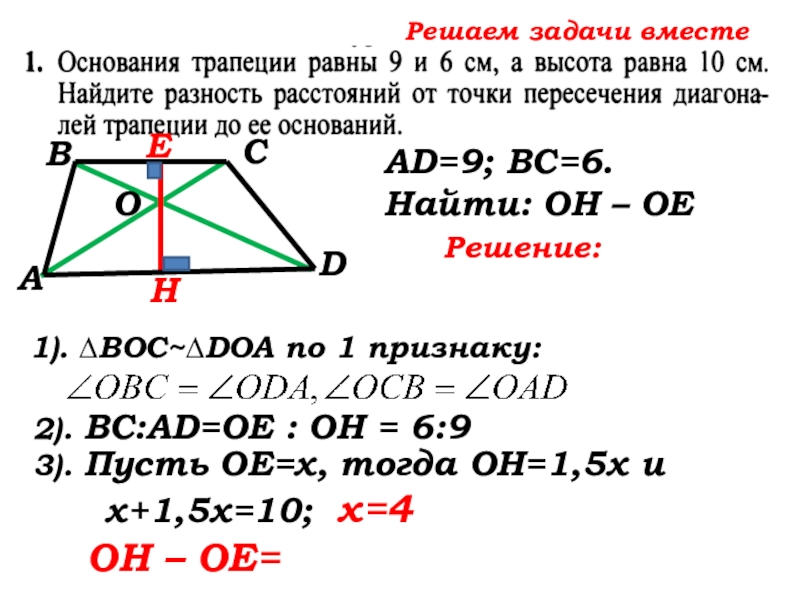
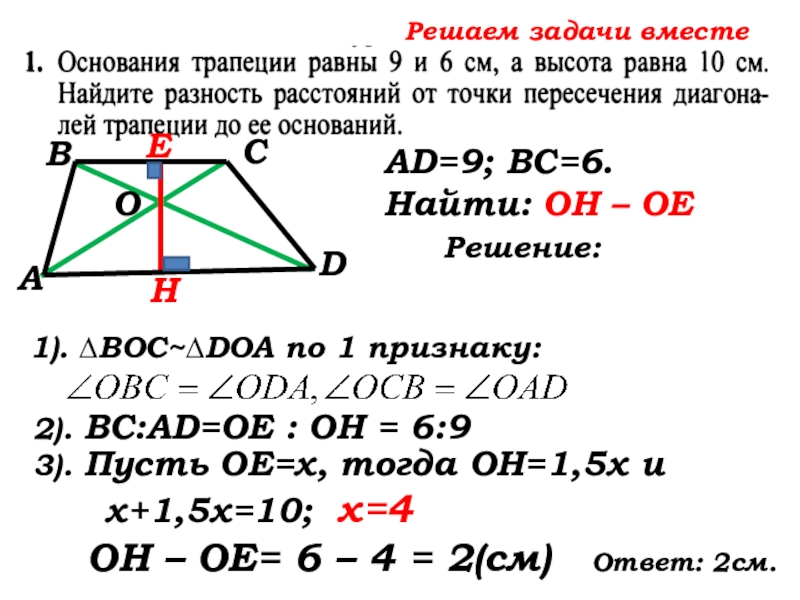
- 46. Решаем задачи вместе САВDНЕОВаши предложения по решению задачиAD=9; ВС=6. Найти: ОН – ОЕ
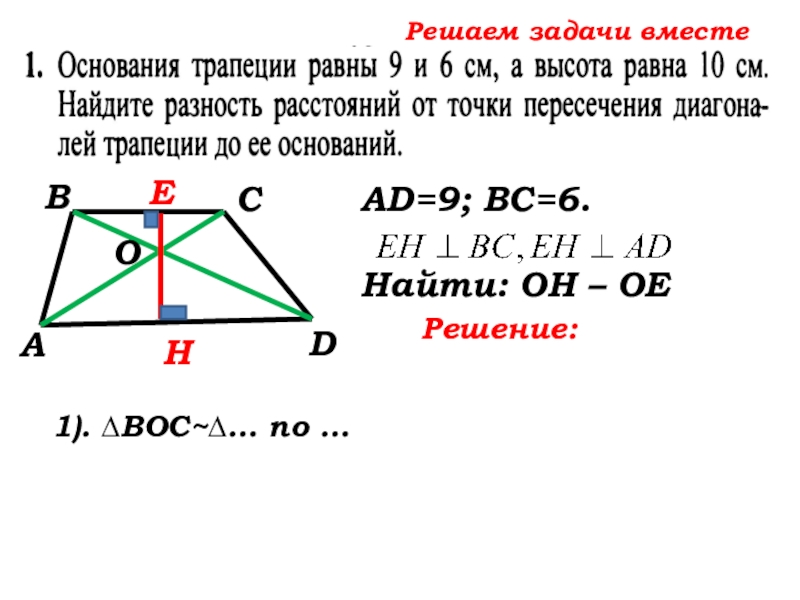
- 47. Решаем задачи вместе САВDНЕО1). ∆ВОС~∆… по
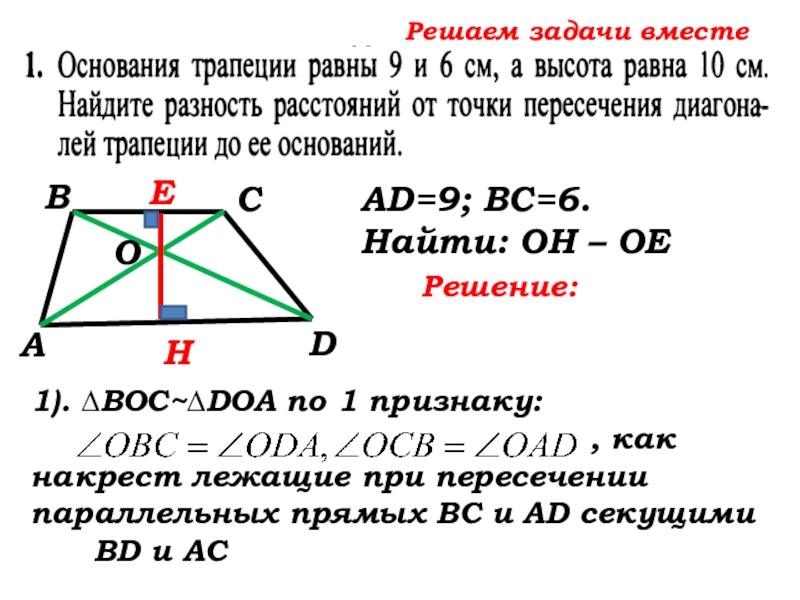
- 48. Решаем задачи вместе САВDНЕО1). ∆ВОС~∆DOA по
- 49. Решаем задачи вместе САВDНЕО1). ∆ВОС~∆DOA по
- 50. Решаем задачи вместе САВDНЕО1). ∆ВОС~∆DOA по
- 51. Решаем задачи вместе САВDНЕО1). ∆ВОС~∆DOA по
- 52. Решаем задачи вместе САВDНЕО1). ∆ВОС~∆DOA по
- 53. Решаем задачи вместе САВDНЕО1). ∆ВОС~∆DOA по
- 54. Решаем задачи вместе САВDНЕ1). ∆ВОС~∆DOA по
- 55. Решаем задачи вместе САВDНЕ1). ∆ВОС~∆DOA по
- 56. Решаем задачи вместе САВDНЕ1). ∆ВОС~∆DOA по
- 57. Решаем задачи вместе САВDНЕ1). ∆ВОС~∆DOA по
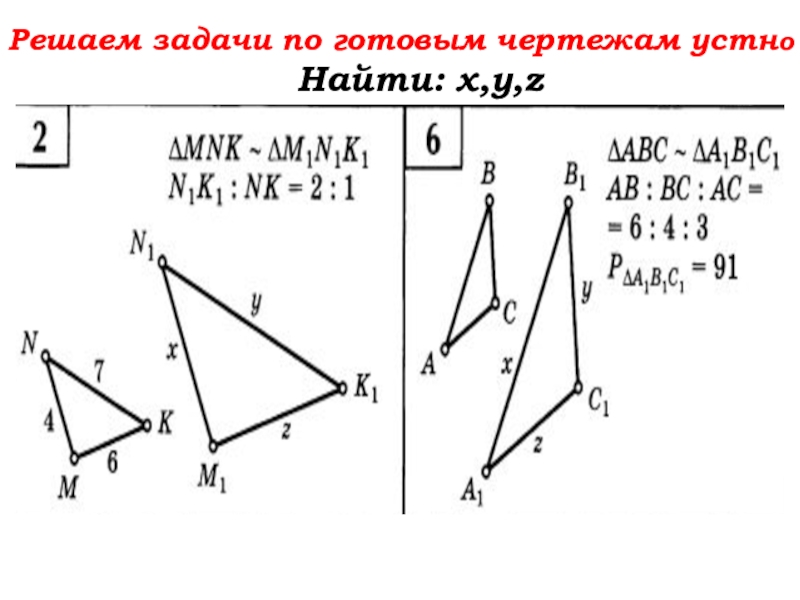
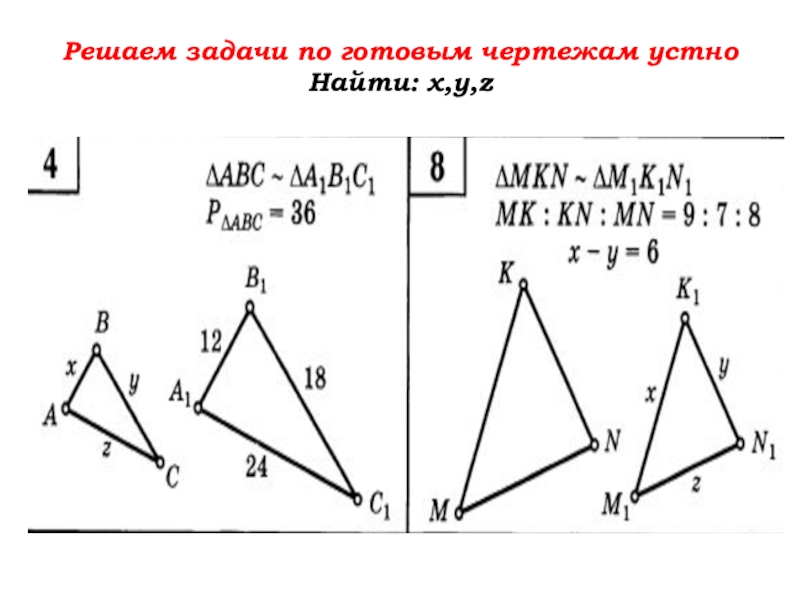
- 58. Решаем задачи по готовым чертежам устно Найти: х,у,z
- 59. Решаем задачи по готовым чертежам устноНайти: х,у,z
- 60. Самостоятельная работа
- 61. Слайд 61
- 62. АВ
- 63. Критерии
- 64. Назовите
- 65. ДР №30 на 16.01.17 Теория: Повторить опр.
- 66. Рекомендации к дополнительной задачеОбозначить:коэффициент пропорциональности за
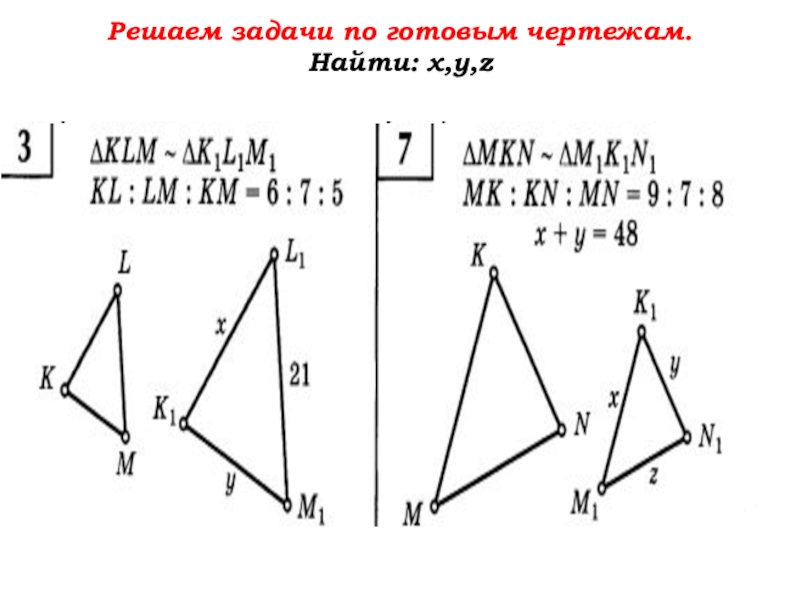
- 67. Решаем задачи по готовым чертежам.Найти: х,у,z
Приветствую вас на уроке геометрии в 8 классе Уроки №48-4912.01.2017 г.
Слайд 1 Урок геометрии в 8 классе с углубленным изучением математики Автор разработки: учитель математики
МБОУ СШ № 10 г. Павлово
Леонтьева Светлана Ивановна
Слайд 3
Успешного усвоения материала
Интересные мысли и высказывания
Высшее
назначение математики - находить порядок в хаосе, который нас окружает.
Н. Винер (1894 - 1964)
Н. Винер (1894 - 1964)
Слайд 7
2. Отрезки АВ и CD называются пропорциональными отрезкам
А1В1 и
C1D1, если …
Отношением двух отрезков называется … их длин
3. Прочитайте словами равенство:
Слайд 8
4. Число k, равное отношению сходственных сторон подобных треугольников, называется
… …
3. Два треугольника называются подобными, если их углы …равны и стороны одного треугольника … сходственным сторонам …
Слайд 9
5. Отношение площадей двух
подобных треугольников
равно
… коэффициента подобия
6. Отношение периметров
подобных треугольников
равно … …
Слайд 10
7. Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные …
… …
(№535)
(№535)
8. Отношение сходственных сторон подобных треугольников равно отношению …, … … … …
(№ 543)
8. Отношение сходственных сторон подобных треугольников равно отношению …, … … … …
(№ 543)
Слайд 11
9. Если два угла одного треугольника … равны … …
другого, то такие треугольники …
10. Если две стороны одного треугольника … двум сторонам другого треугольника и углы, … … этими сторонами, равны, то такие треугольники …
Слайд 12
11. Если три стороны одного треугольника … трем сторонам другого
треугольника, то такие треугольники …
12. Если два треугольника подобны, то их … стороны …,
а соответственные углы …
Слайд 13
13. Треугольники АВС и KDN подобны
Назовите
пропорциональные стороны.
2) Назовите равные
углы.
Слайд 14
14. Все круги между собой …
Коэффициент подобия равен отношению
… .
15. Все квадраты между собой … Коэффициент подобия равен отношению … .
16. Все равносторонние треугольники между собой …
Коэффициент подобия равен отношению … .
Слайд 15
17. Если сторона первого квадрата в 2 раза меньше стороны
второго, то площадь его … в … раз.
18. Если сторона одного равностороннего треугольника больше стороны другого в 4 раза, то его площадь … в …раз.
19. Если радиус одного круга больше радиуса другого в 5 раз, то его площадь … в … раз.
Слайд 18Закрепить теоретические знания по теме.
Формировать навыки применения признаков подобия
треугольников при решении задач.
Формировать правильную математическую речь, совершенствовать навыки решения задач.
Формировать правильную математическую речь, совершенствовать навыки решения задач.
Цели урока:
Слайд 24
Проверка
Решение:
Так как
по теореме Пифагора:
Треугольники являются подобными по 2 признаку
Слайд 25
Решаем задачу в группах
Проверка
КМ=
Группа 1-
а)
Группа 2-
б)
Группа 3-
в)
Каждой группой решается вся задача
Отчёт
Слайд 27
Проверка
КМ=
М
К
N
E
F
6
9
MK=10
KN=15
Решение:
EF║KM, по условию,
∆KEF~∆KMN по 1 признаку, по 2-м углам:
Слайд 28
Проверка
КМ=
М
К
N
E
F
6
9
MK=10
KN=15
Решение:
EF║KM, по условию,
∆KEF~∆KMN по 1 признаку, по 2-м углам:
Слайд 29
Проверка
КМ=
М
К
N
E
F
6
9
MK=10
KN=15
Решение:
EF║KM, по условию,
∆KEF~∆KMN по 1 признаку, по 2-м углам:
Слайд 30
Проверка
КМ=
М
К
N
E
F
6
9
MK=10
KN=15
Решение:
EF║KM, по условию,
∆KEF~∆KMN по 1 признаку, по 2-м углам:
Слайд 35
А
В
С
D
E
K
Р
М
Решение:
Проведём KD║BE, тогда ВКDE-параллелограмм
и
АЕ=ED=BK=KC.
По теореме Фалеса:
АЕ=ED=BK=KC.
По теореме Фалеса:
т.к. АЕ=ED, то АР=РМ
Слайд 36
А
В
С
D
E
K
Р
М
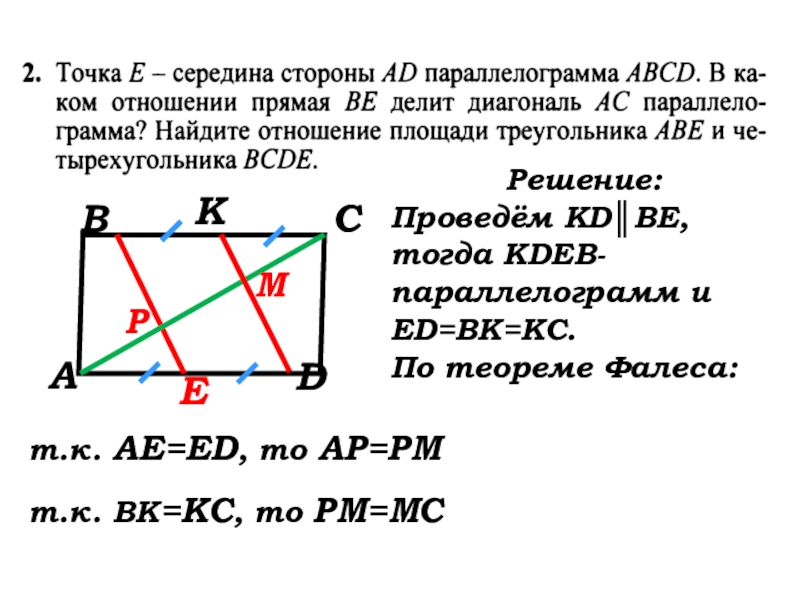
Решение:
Проведём KD║BE, тогда КDEB-параллелограмм
и
ED=BK=KC.
По теореме Фалеса:
ED=BK=KC.
По теореме Фалеса:
т.к. АЕ=ED, то АР=РМ
т.к. ВК=КС, то РМ=МС
Слайд 37
А
В
С
D
E
K
Р
М
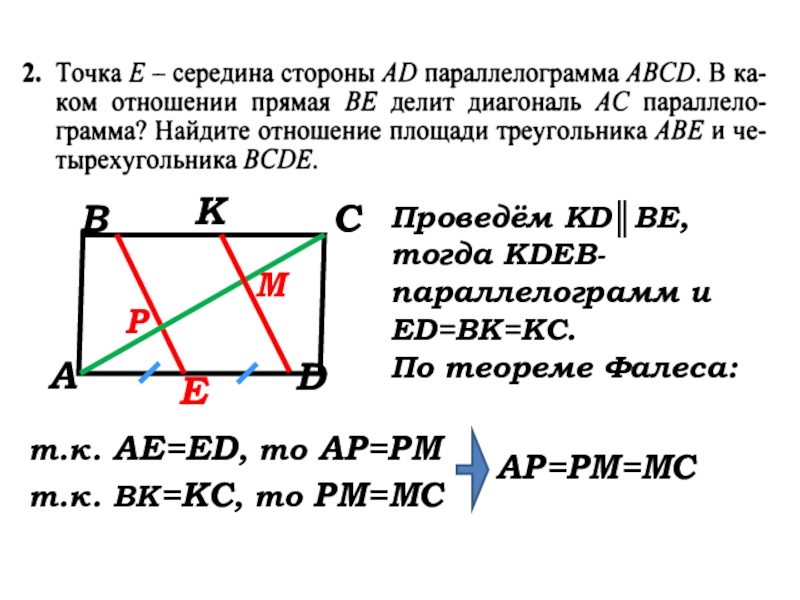
Проведём KD║BE, тогда КDEB-параллелограмм
и
ED=BK=KC.
По теореме Фалеса:
ED=BK=KC.
По теореме Фалеса:
т.к. АЕ=ED, то АР=РМ
т.к. ВК=КС, то РМ=МС
АР=РМ=МС
Слайд 38
А
В
С
D
E
K
Р
М
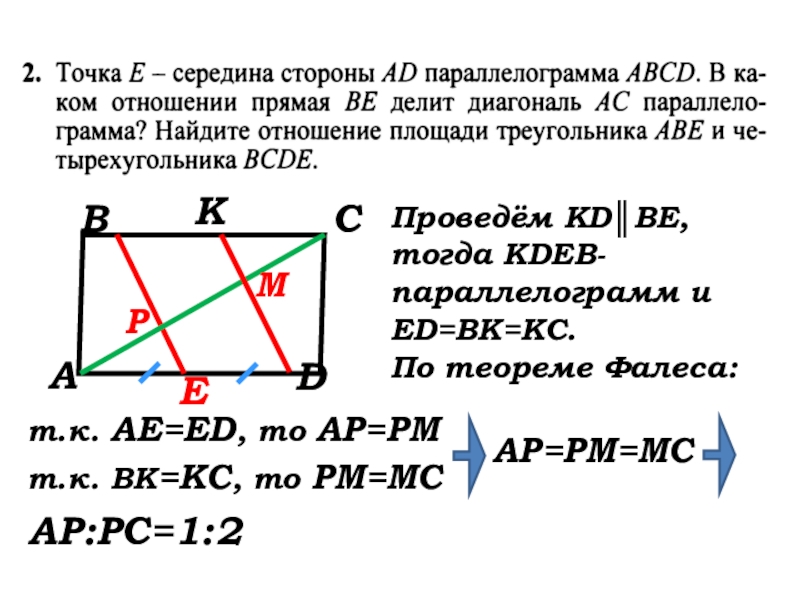
Проведём KD║BE, тогда КDEB-параллелограмм
и
ED=BK=KC.
По теореме Фалеса:
ED=BK=KC.
По теореме Фалеса:
т.к. АЕ=ED, то АР=РМ
т.к. ВК=КС, то РМ=МС
АР=РМ=МС
АР:РС=1:2
Слайд 44
Решаем задачи вместе
Что не построено
на чертеже?
Что нужно провести,
чтобы указать расстояния?
Слайд 48
Решаем задачи вместе
С
А
В
D
Н
Е
О
1). ∆ВОС~∆DOA по 1 признаку:
, как …
AD=9; ВС=6. Найти: ОН – ОЕ
Решение:
Слайд 49
Решаем задачи вместе
С
А
В
D
Н
Е
О
1). ∆ВОС~∆DOA по 1 признаку:
, как накрест лежащие при пересечении параллельных прямых ВС и AD секущими
BD и АС
BD и АС
AD=9; ВС=6. Найти: ОН – ОЕ
Решение:
Слайд 50
Решаем задачи вместе
С
А
В
D
Н
Е
О
1). ∆ВОС~∆DOA по 1 признаку:
AD=9; ВС=6.
Найти: ОН – ОЕ
Решение:
Решение:
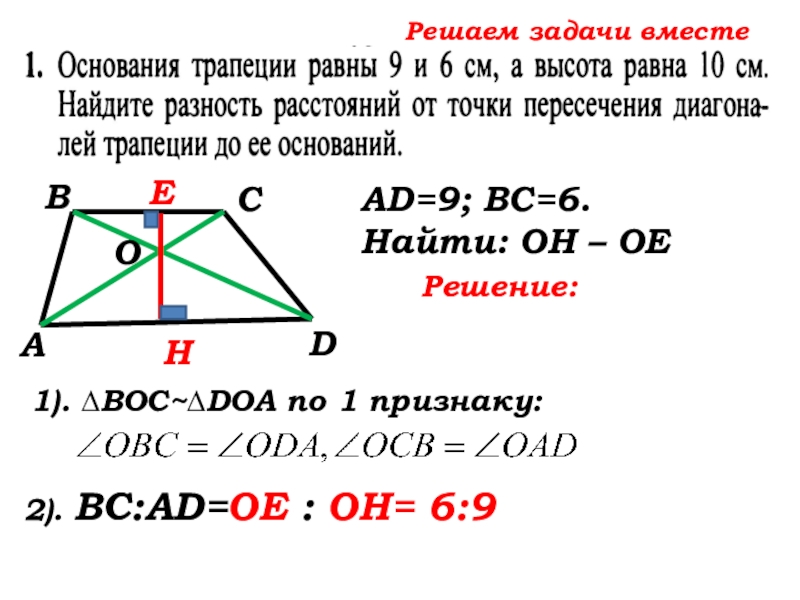
2). ВС:AD=… : … =
Слайд 51
Решаем задачи вместе
С
А
В
D
Н
Е
О
1). ∆ВОС~∆DOA по 1 признаку:
AD=9; ВС=6.
Найти: ОН – ОЕ
Решение:
Решение:
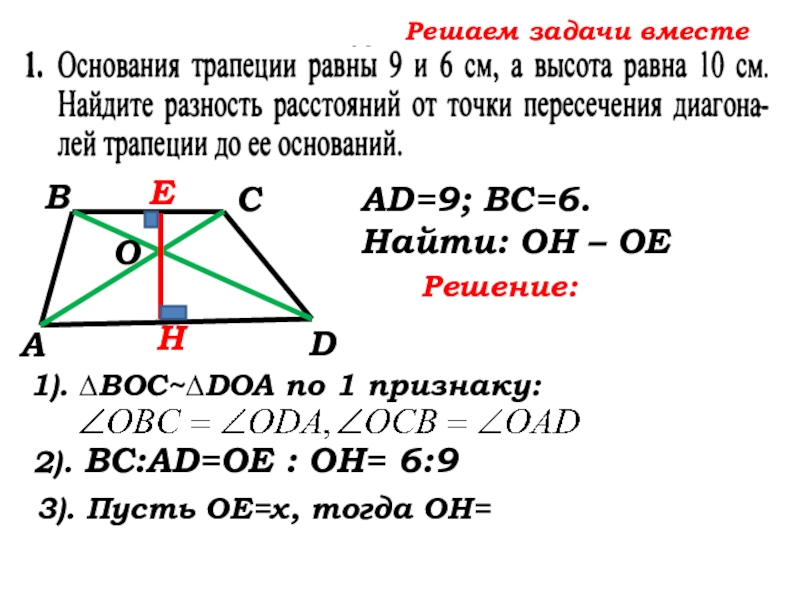
2). ВС:AD=ОЕ : ОН= 6:9
Слайд 52
Решаем задачи вместе
С
А
В
D
Н
Е
О
1). ∆ВОС~∆DOA по 1 признаку:
AD=9; ВС=6.
Найти: ОН – ОЕ
Решение:
Решение:
2). ВС:AD=ОЕ : ОН= 6:9
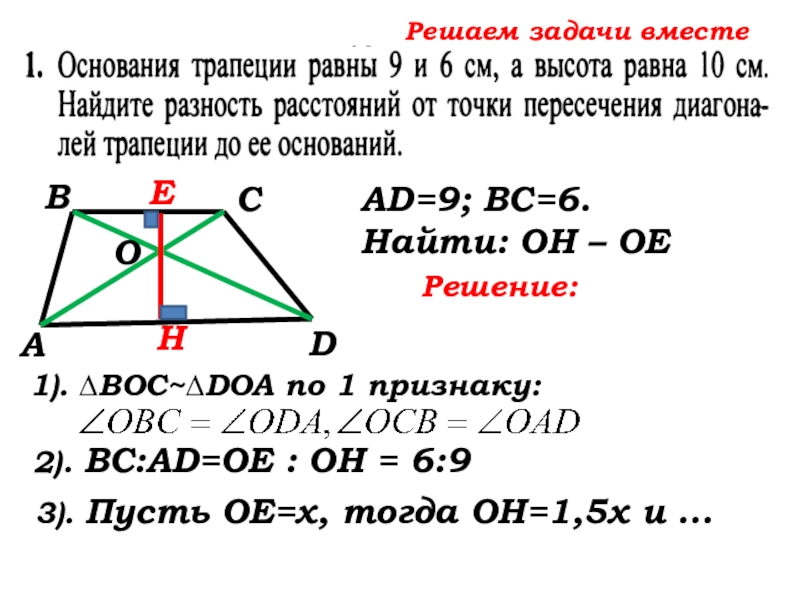
3). Пусть ОЕ=х, тогда ОН=
Слайд 53
Решаем задачи вместе
С
А
В
D
Н
Е
О
1). ∆ВОС~∆DOA по 1 признаку:
AD=9; ВС=6.
Найти: ОН – ОЕ
Решение:
Решение:
2). ВС:AD=ОЕ : ОН = 6:9
3). Пусть ОЕ=х, тогда ОН=1,5х и …
Слайд 54
Решаем задачи вместе
С
А
В
D
Н
Е
1). ∆ВОС~∆DOA по 1 признаку:
AD=9; ВС=6.
Найти: ОН – ОЕ
Решение:
Решение:
2). ВС:AD=ОЕ : ОН = 6:9
3). Пусть ОЕ=х, тогда ОН=1,5х и
х+1,5х=10
Слайд 55
Решаем задачи вместе
С
А
В
D
Н
Е
1). ∆ВОС~∆DOA по 1 признаку:
AD=9; ВС=6.
Найти: ОН – ОЕ
Решение:
Решение:
2). ВС:AD=ОЕ : ОН = 6:9
3). Пусть ОЕ=х, тогда ОН=1,5х и
х+1,5х=10; х=4
Слайд 56
Решаем задачи вместе
С
А
В
D
Н
Е
1). ∆ВОС~∆DOA по 1 признаку:
AD=9; ВС=6.
Найти: ОН – ОЕ
Решение:
Решение:
2). ВС:AD=ОЕ : ОН = 6:9
3). Пусть ОЕ=х, тогда ОН=1,5х и
х+1,5х=10; х=4
ОН – ОЕ=
Слайд 57
Решаем задачи вместе
С
А
В
D
Н
Е
1). ∆ВОС~∆DOA по 1 признаку:
AD=9; ВС=6.
Найти: ОН – ОЕ
Решение:
Решение:
2). ВС:AD=ОЕ : ОН = 6:9
3). Пусть ОЕ=х, тогда ОН=1,5х и
х+1,5х=10; х=4
ОН – ОЕ= 6 – 4 = 2(см) Ответ: 2см.
Слайд 63
Критерии оценки за урок:
1.
Комментировали ДЗ
2. Активно участвовали в решении устных задач.
3. Привели решение задач, решаемых письменно
2. Активно участвовали в решении устных задач.
3. Привели решение задач, решаемых письменно
Поставьте себе оценку за урок
Слайд 65ДР №30 на 16.01.17
Теория: Повторить опр. подобных треугольников, выводы из
задач, формулировку 3-х признаков подобия треугольников
Практика: разобрать классные задачи.
1. Прорешать задачи самостоятельной работы следующего уровня на отдельном листе. Сдать 16.01.
Дополнительная задача
КР№3 -2февраля
Практика: разобрать классные задачи.
1. Прорешать задачи самостоятельной работы следующего уровня на отдельном листе. Сдать 16.01.
Дополнительная задача
КР№3 -2февраля
Дополнительные задачи
Слайд 66
Рекомендации к дополнительной задаче
Обозначить:
коэффициент пропорциональности за k,
катет одного треугольника
за а, гипотенузу за с; а другого соответственно за а1 и с1.
По теореме Пифагора найти другой катет каждого треугольника и показать, что стороны треугольников пропорциональны.
По теореме Пифагора найти другой катет каждого треугольника и показать, что стороны треугольников пропорциональны.
