- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Решение практических задач с помощью теоремы Пифагора
Содержание
- 1. Презентация по геометрии Решение практических задач с помощью теоремы Пифагора
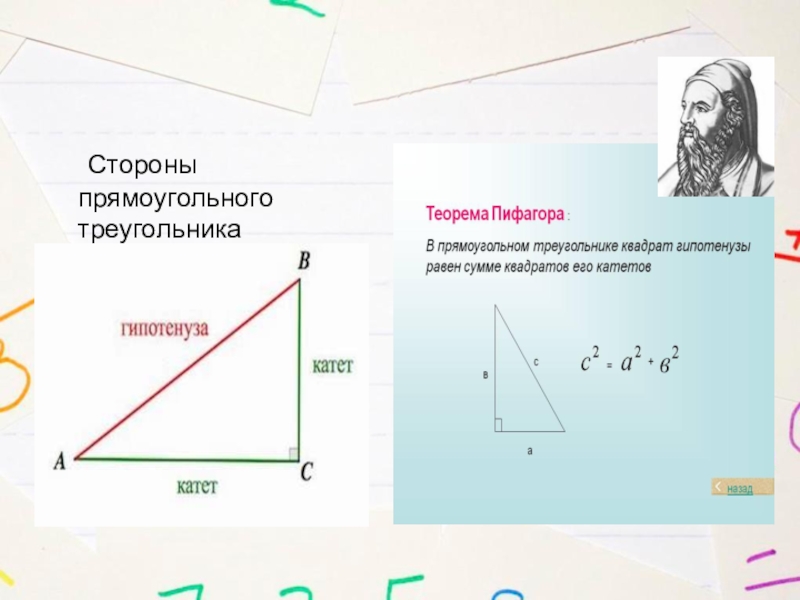
- 2. Стороны прямоугольного треугольника
- 3. Слайд 3
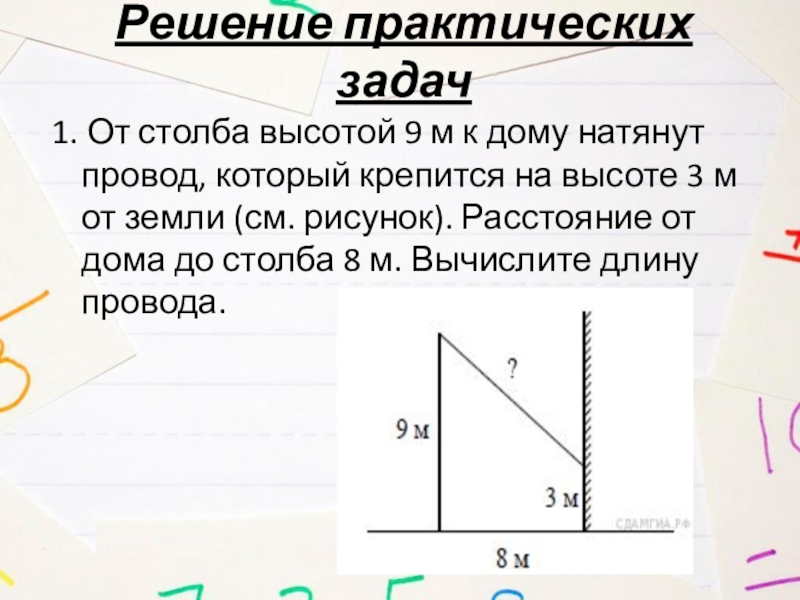
- 4. Решение практических задач1. От столба высотой 9
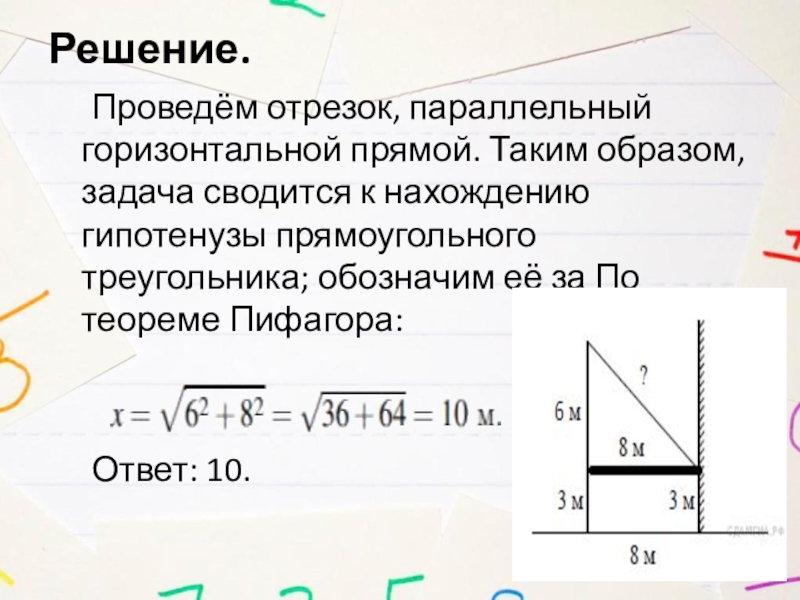
- 5. Решение. Проведём отрезок, параллельный горизонтальной прямой. Таким
- 6. 2. Лестницу длиной 3 м прислонили к
- 7. Решение Задача сводится к нахождению катета прямоугольного треугольника, по теореме Пифагора он равен: Ответ: 2,4.
- 8. 3. Мальчик прошел от дома по направлению
- 9. Решение Мальчик идёт вдоль сторон прямоугольного треугольника поэтому, искомое расстояние можно найти по теореме Пифагора: Ответ: 1000.
- 10. 4. Девочка прошла от дома по направлению
- 11. Решение Девочка идёт вдоль прямоугольной трапеции, в которой
- 12. 6. Глубина крепостного рва равна 8 м, ширина
- 13. Решение Расстояние AB — гипотенуза прямоугольного треугольника с
- 14. Лестница соединяет точки A и B и
- 15. Высота и длина каждой ступени составляют катеты
- 16. 7. Точка крепления троса, удерживающего флагшток в
- 17. Решение Задачу можно свести к нахождению гипотенузы прямоугольного
- 18. 8. От столба к дому натянут провод
- 19. Решение Проведём отрезок, параллельный горизонтальной прямой. Таким образом,
- 20. Длина стремянки в сложенном виде равна 1,85
- 21. Решение Данная задача сводится к нахождению катета прямоугольного треугольника. Пусть — искомое расстояние, тогда: Ответ: 2,22.
- 22. 10. Пожарную лестницу длиной 13 м приставили
- 23. Решение Задача сводится к нахождению катета прямоугольного треугольника: Ответ: 12.
- 24. Домашнее задание 1. Почему теорема долгое время называлась "теоремой невесты"? 2. Какие треугольники называют пифагоровыми?
Стороны прямоугольного треугольника
Слайд 4Решение практических задач
1. От столба высотой 9 м к дому натянут
провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.
Слайд 5Решение.
Проведём отрезок, параллельный горизонтальной прямой. Таким образом, задача сводится к нахождению
гипотенузы прямоугольного треугольника; обозначим её за По теореме Пифагора:
Ответ: 10.
Ответ: 10.
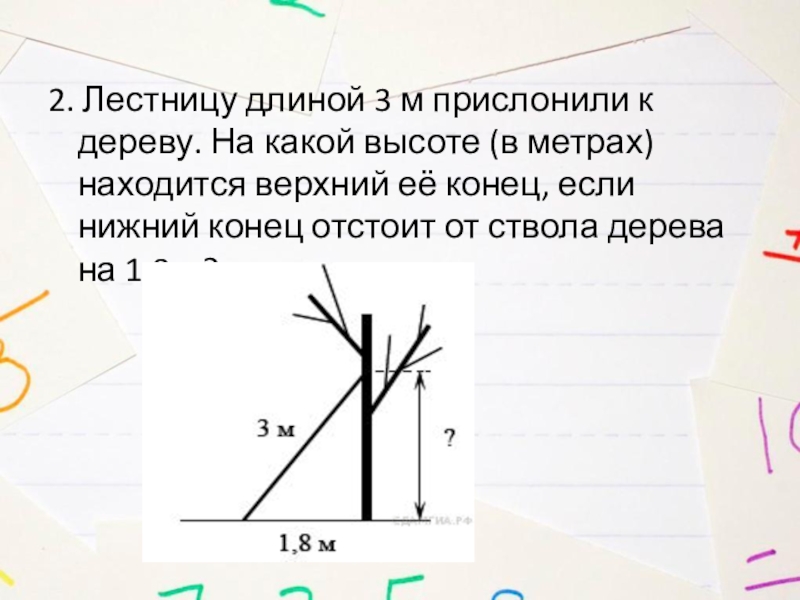
Слайд 62. Лестницу длиной 3 м прислонили к дереву. На какой высоте
(в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
Слайд 7Решение
Задача сводится к нахождению катета прямоугольного треугольника, по теореме Пифагора он
равен:
Ответ: 2,4.
Ответ: 2,4.
Слайд 83. Мальчик прошел от дома по направлению на восток 800 м.
Затем повернул на север и прошел 600 м. На каком расстоянии (в метрах) от дома оказался мальчик?
Слайд 9Решение
Мальчик идёт вдоль сторон прямоугольного треугольника поэтому, искомое расстояние можно найти
по теореме Пифагора:
Ответ: 1000.
Ответ: 1000.
Слайд 104. Девочка прошла от дома по направлению на запад 500 м.
Затем повернула на север и прошла 300 м. После этого она повернула на восток и прошла еще 100 м. На каком расстоянии (в метрах) от дома оказалась девочка?
Слайд 11Решение
Девочка идёт вдоль прямоугольной трапеции, в которой длина боковой стороны, не
перпендикулярной основаниям, есть искомое расстояние, которое можно найти по теореме Пифагора:
Ответ: 500.
Ответ: 500.
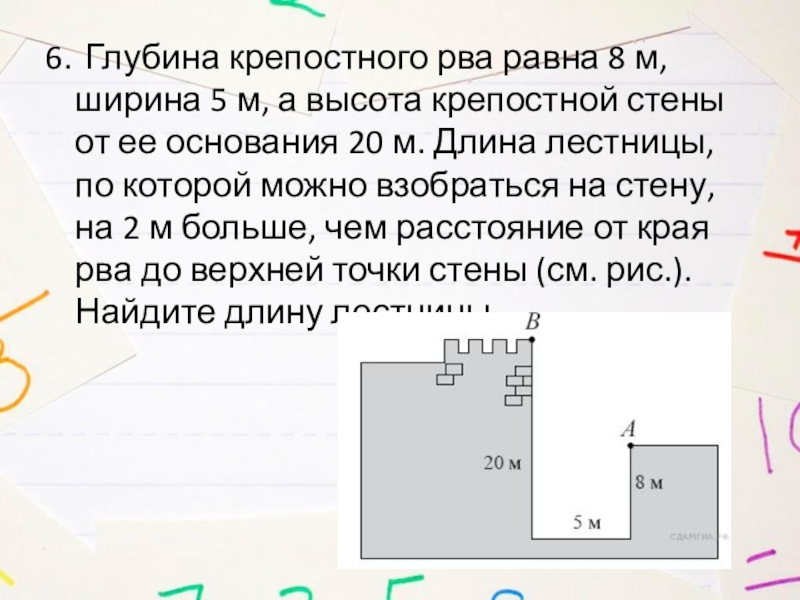
Слайд 126. Глубина крепостного рва равна 8 м, ширина 5 м, а высота
крепостной стены от ее основания 20 м. Длина лестницы, по которой можно взобраться на стену, на 2 м больше, чем расстояние от края рва до верхней точки стены (см. рис.). Найдите длину лестницы.
Слайд 13Решение
Расстояние AB — гипотенуза прямоугольного треугольника с катетами 5 м и 20 − 8 = 12 м.
Тем самым, длина AB равна 13 м, а длина лестницы равна 15 м.
Ответ: 15.
Ответ: 15.
Слайд 14 Лестница соединяет точки A и B и состоит из 35 ступеней.
Высота каждой ступени равна 14 см, а длина — 48 см. Найдите расстояние между точками A и B (в метрах).
Слайд 15 Высота и длина каждой ступени составляют катеты прямоугольного треугольника, найдём гипотенузу
этого треугольника по теореме Пифагора:
Всего ступеней 35, следовательно, расстояние между точками A и B равно 50 · 35 = 1750 см = 17,5 м.
Ответ: 17,5.
Всего ступеней 35, следовательно, расстояние между точками A и B равно 50 · 35 = 1750 см = 17,5 м.
Ответ: 17,5.
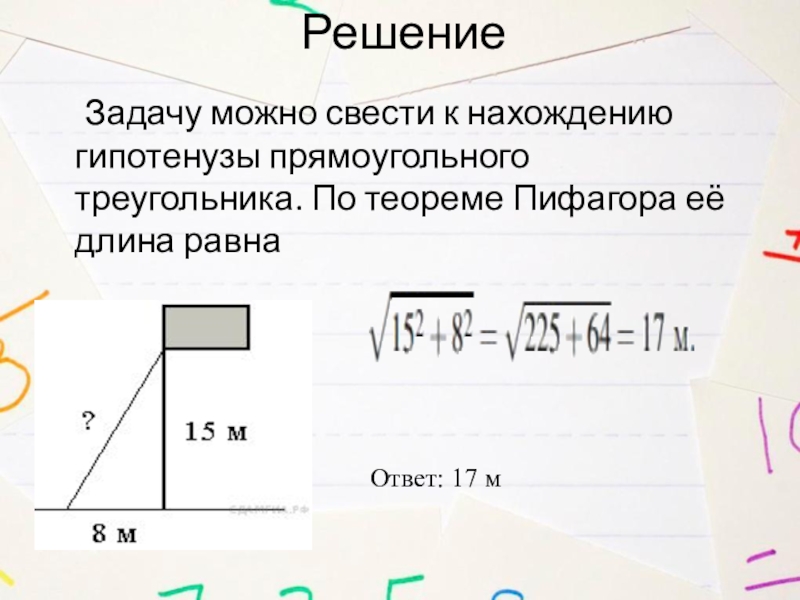
Слайд 167. Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на
высоте 15 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 8 м. Найдите длину троса.
Слайд 17Решение
Задачу можно свести к нахождению гипотенузы прямоугольного треугольника. По теореме Пифагора
её длина равна
Ответ: 17 м
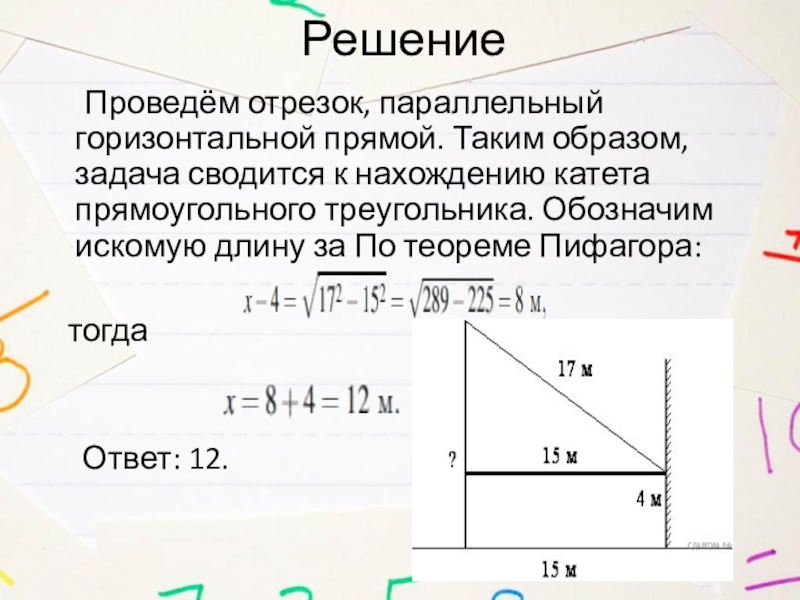
Слайд 188. От столба к дому натянут провод длиной 17 м, который
закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 15 м.
Слайд 19Решение
Проведём отрезок, параллельный горизонтальной прямой. Таким образом, задача сводится к нахождению
катета прямоугольного треугольника. Обозначим искомую длину за По теореме Пифагора:
тогда
Ответ: 12.
тогда
Ответ: 12.
Слайд 20 Длина стремянки в сложенном виде равна 1,85 м, а её высота
в разложенном виде составляет 1,48 м. Найдите расстояние (в метрах) между основаниями стремянки в разложенном виде.
Слайд 21Решение
Данная задача сводится к нахождению катета прямоугольного треугольника. Пусть — искомое
расстояние, тогда:
Ответ: 2,22.
Ответ: 2,22.
Слайд 2210. Пожарную лестницу длиной 13 м приставили к окну пятого этажа
дома. Нижний конец лестницы отстоит от стены на 5 м. На какой высоте расположено окно? Ответ дайте в метрах.
Слайд 24Домашнее задание
1. Почему теорема долгое время называлась "теоремой невесты"?
2. Какие
треугольники называют пифагоровыми?