бегать на лыжах. Ему можно научиться только путем подражания или упражнения.
Д. Пойа
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
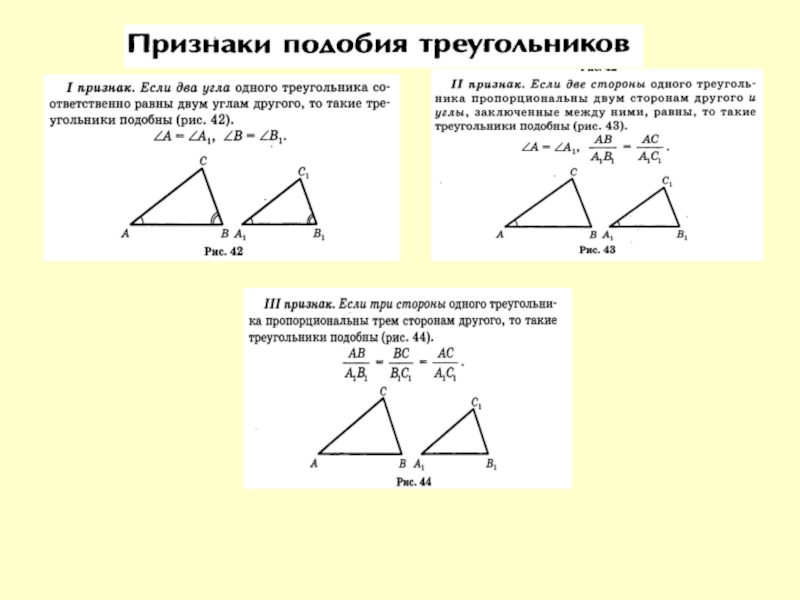
Презентация, доклад по геометрии Применение подобия треугольников
Содержание
- 1. Презентация по геометрии Применение подобия треугольников
- 2. Применение подобия треугольников к решению задач.
- 3. Слайд 3
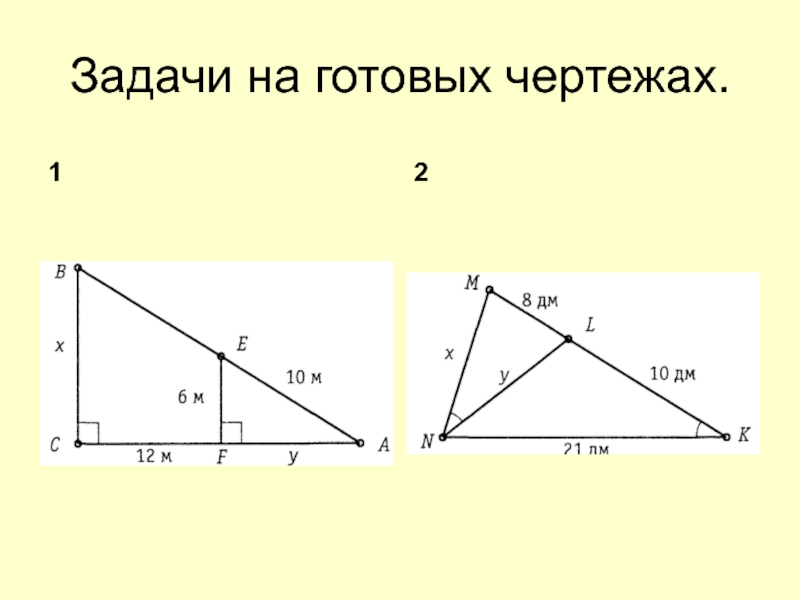
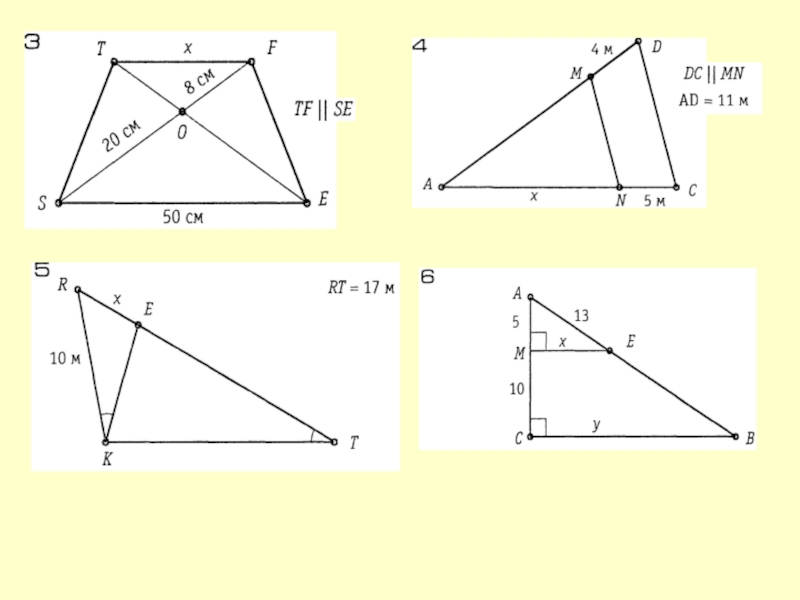
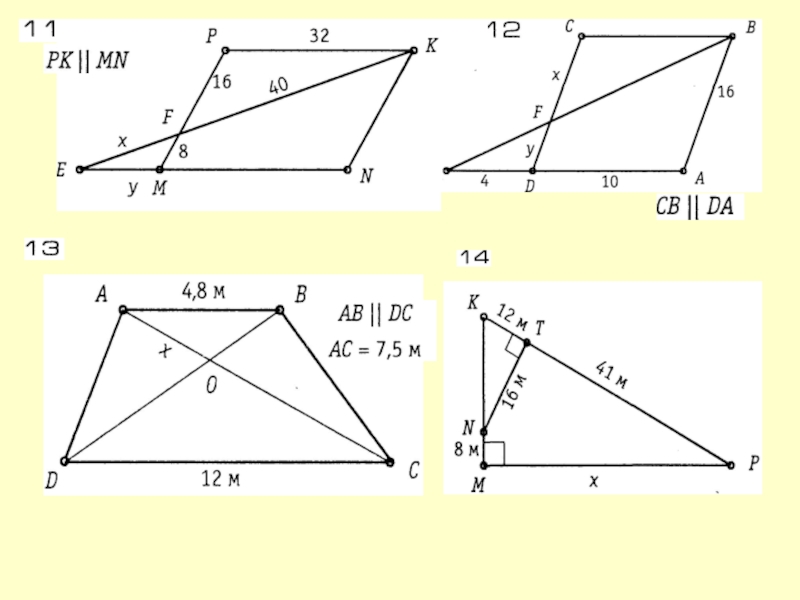
- 4. Задачи на готовых чертежах.12
- 5. Слайд 5
- 6. Слайд 6
- 7. Слайд 7
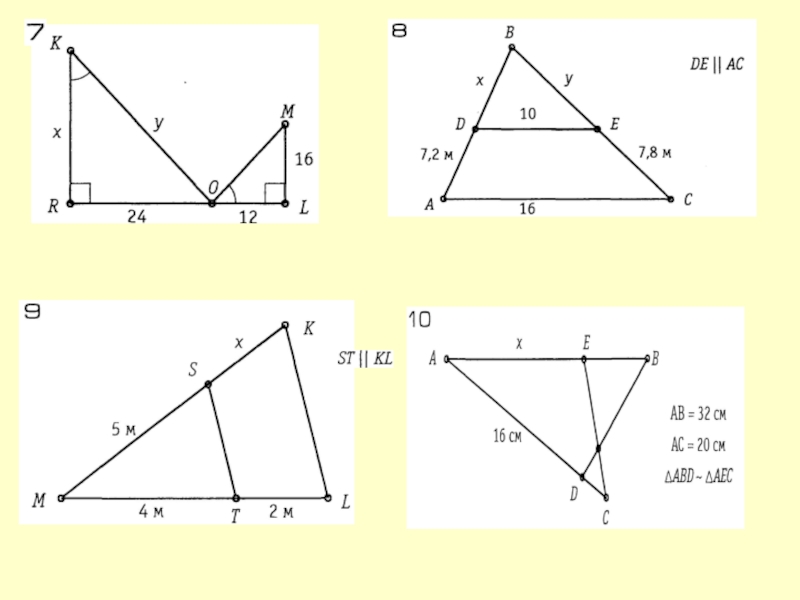
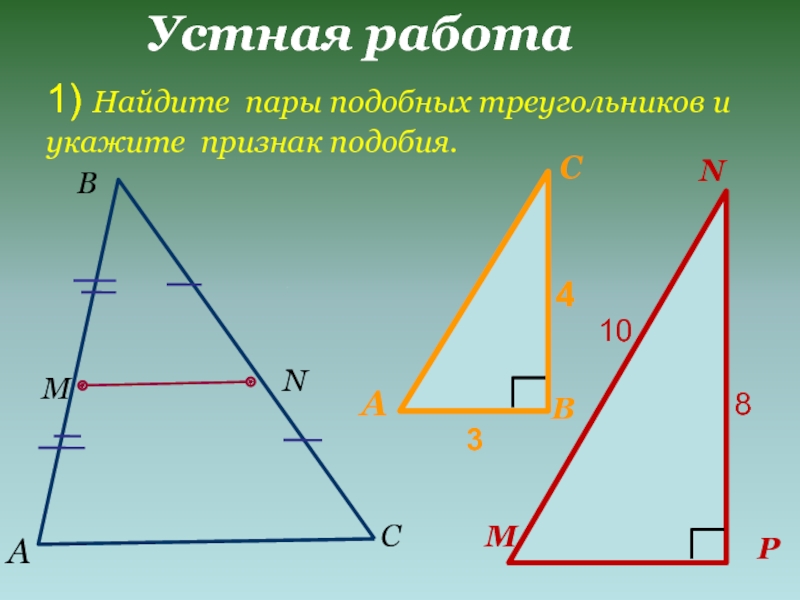
- 8. Устная работа1) Найдите пары подобных треугольников и укажите признак подобия.АВСМN34810АВСMNP
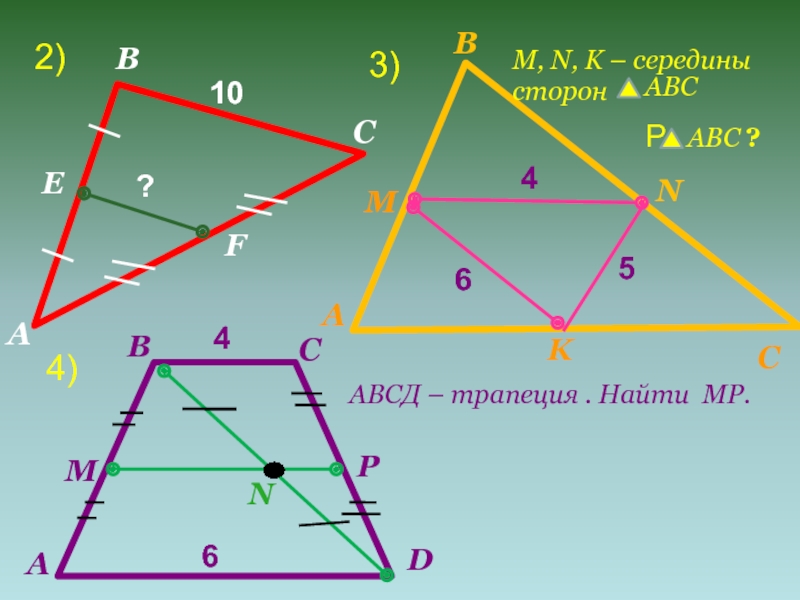
- 9. 2)АBCEF10?АBCMNK465M, N, K – середины сторон АВС PАВС ?АBCDMNP46АВСД – трапеция . Найти МР.3)4)
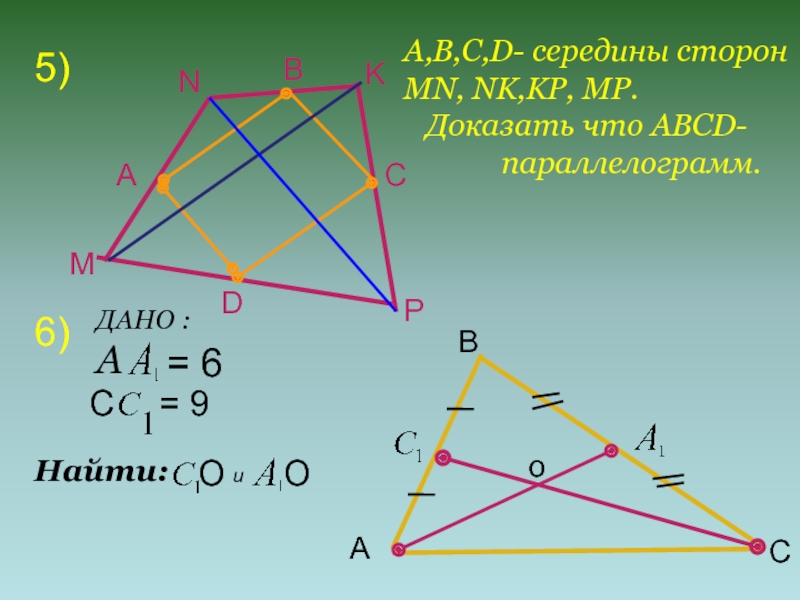
- 10. 5)МNKPАBCDА,В,С,D- середины сторон MN, NK,KP, MP.
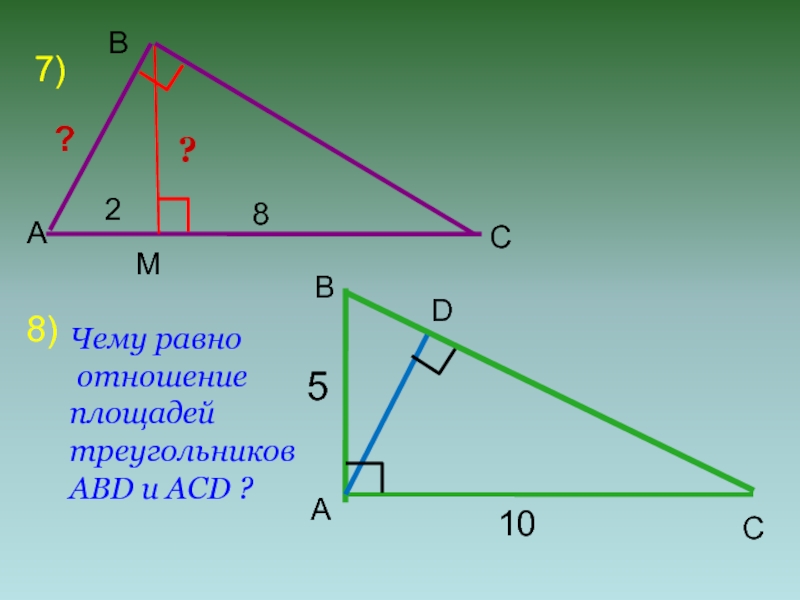
- 11. 7)МАBC?8)ABC28?D510Чему равно отношение площадей треугольниковABD и ACD ?
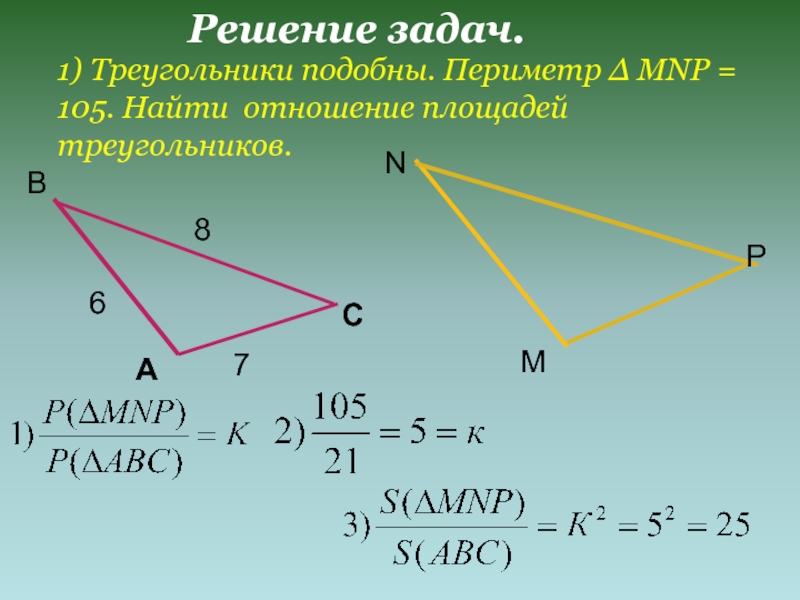
- 12. Решение задач.ABC687MNP1) Треугольники подобны. Периметр Δ MNP = 105. Найти отношение площадей треугольников.
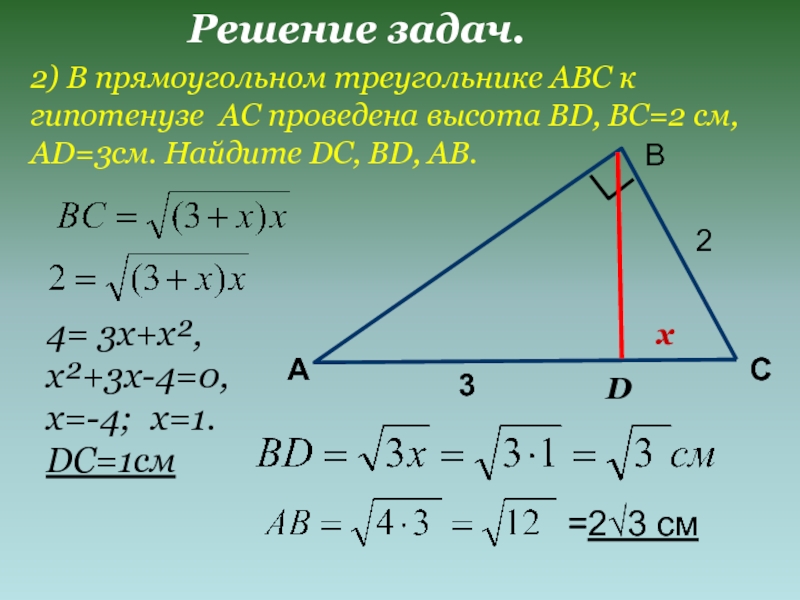
- 13. Решение задач.ABC2) В прямоугольном треугольнике ABC
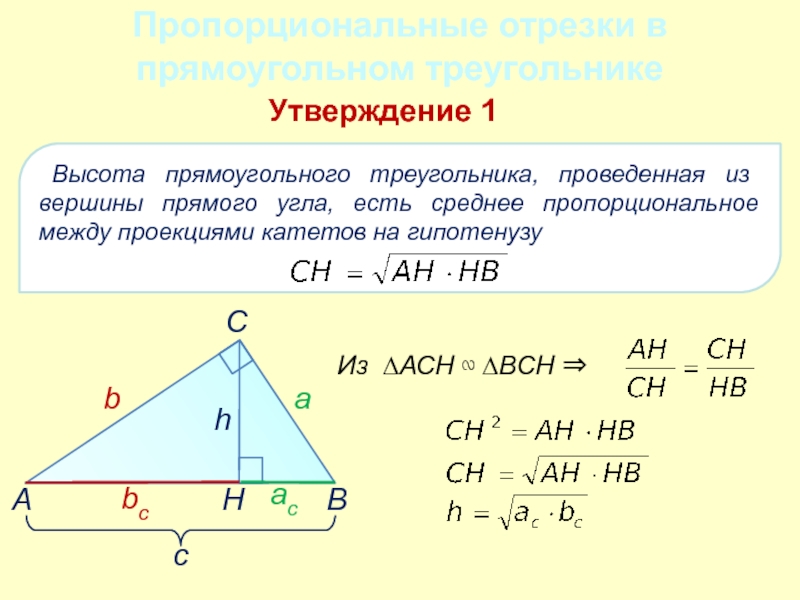
- 14. Пропорциональные отрезки в прямоугольном треугольникеУтверждение 1 Высота
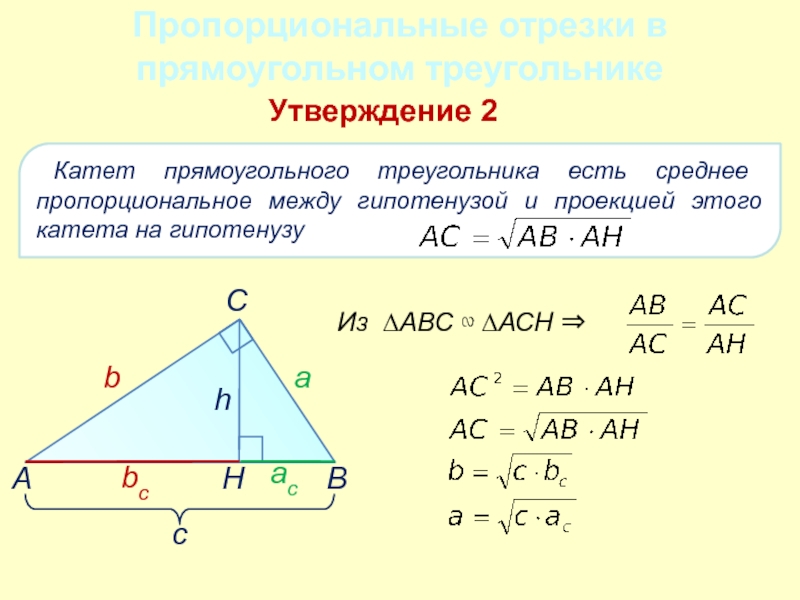
- 15. Пропорциональные отрезки в прямоугольном треугольникеУтверждение 2 Катет
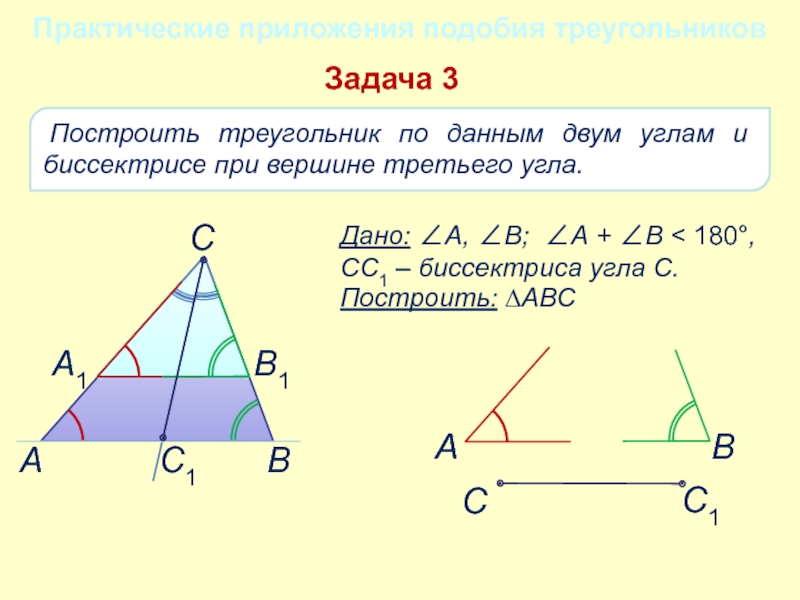
- 16. Построить треугольник по данным двум углам
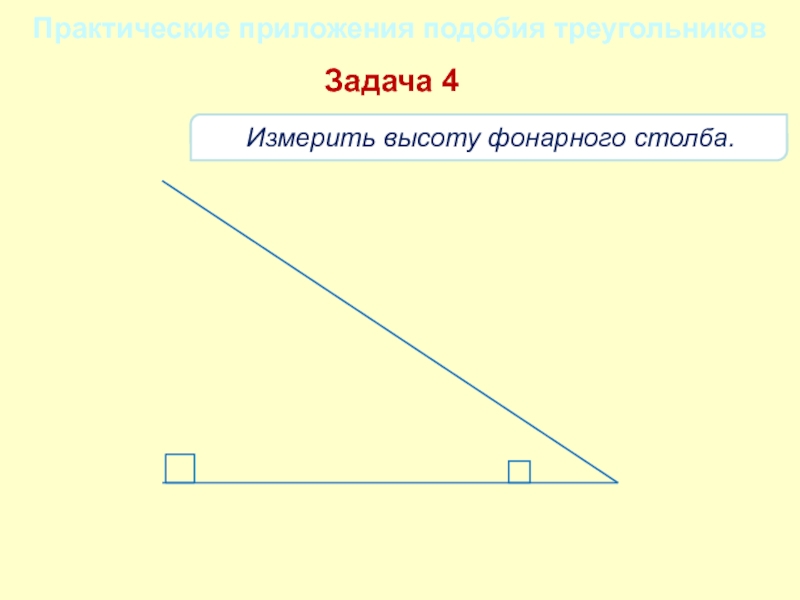
- 17. Измерить высоту фонарного столба.Практические приложения подобия треугольниковЗадача 42,14,21,7?АВСА1С1Из ∆АВС ∾ ∆А1ВС1
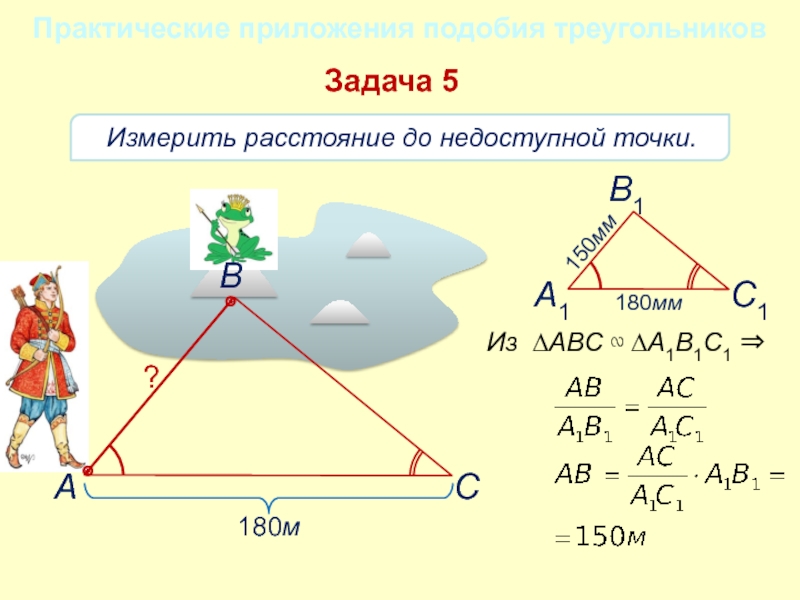
- 18. Измерить расстояние до недоступной точки.Практические приложения подобия треугольниковЗадача 5180м?АСВИз ∆АВС ∾ ∆А1В1С1
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. Слайд 24
Применение подобия треугольников к решению задач.
Слайд 8Устная работа
1) Найдите пары подобных треугольников и
укажите признак подобия.
А
В
С
М
N
3
4
8
10
А
В
С
M
N
P
Слайд 92)
А
B
C
E
F
10
?
А
B
C
M
N
K
4
6
5
M, N, K – середины
сторон
АВС
P
АВС ?
А
B
C
D
M
N
P
4
6
АВСД
– трапеция . Найти МР.
3)
4)
Слайд 105)
М
N
K
P
А
B
C
D
А,В,С,D- середины сторон
MN, NK,KP, MP.
Доказать что ABCD-
параллелограмм.
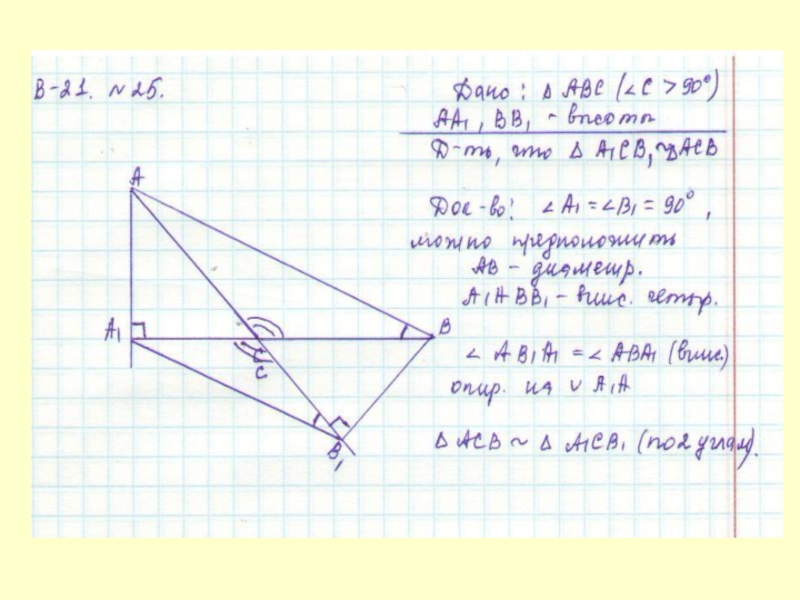
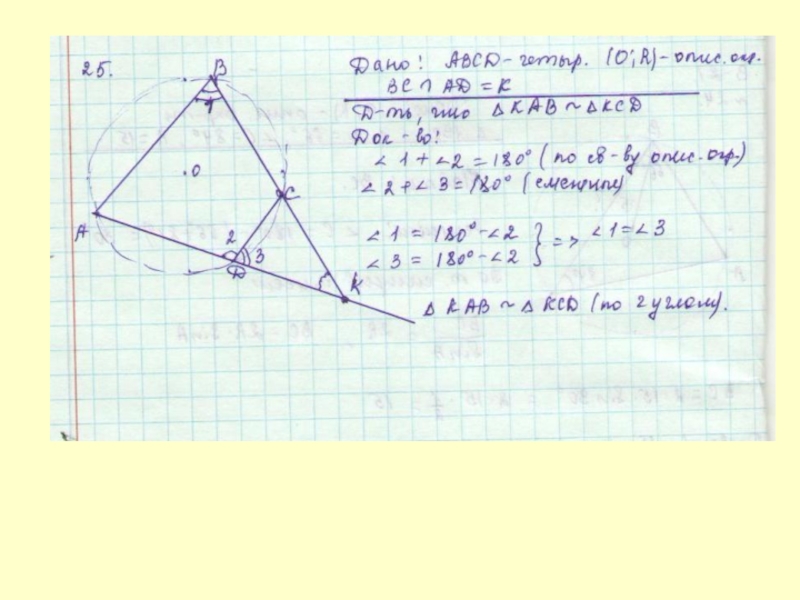
6)
A
B
C
O
o
А
= 6
C
= 9
ДАНО :
Найти:
O
и
Слайд 12
Решение задач.
A
B
C
6
8
7
M
N
P
1) Треугольники подобны. Периметр Δ MNP = 105. Найти
отношение площадей треугольников.
Слайд 13
Решение задач.
A
B
C
2) В прямоугольном треугольнике ABC к гипотенузе AC проведена
высота BD, BC=2 см, AD=3см. Найдите DC, BD, AB.
D
2
3
х
4= 3х+х²,
х²+3х-4=0,
х=-4; х=1. DC=1см
=2√3 см
Слайд 14Пропорциональные отрезки в прямоугольном треугольнике
Утверждение 1
Высота прямоугольного треугольника, проведенная из
вершины прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу
Из ∆АСН ∾ ∆ВСН
bc
ac
a
b
h
c
Слайд 15Пропорциональные отрезки в прямоугольном треугольнике
Утверждение 2
Катет прямоугольного треугольника есть среднее
пропорциональное между гипотенузой и проекцией этого катета на гипотенузу
Из ∆АВС ∾ ∆АСН
bc
ac
a
b
h
c
Слайд 16 Построить треугольник по данным двум углам и биссектрисе при вершине
третьего угла.
А
В
С
А1
В1
Дано: А, В; А + В < 180,
СС1 – биссектриса угла С.
Построить: ∆АВС
Практические приложения подобия треугольников
С1
Задача 3
А
В
С
С1
Слайд 17 Измерить высоту фонарного столба.
Практические приложения подобия треугольников
Задача 4
2,1
4,2
1,7
?
А
В
С
А1
С1
Из ∆АВС ∾
∆А1ВС1
Слайд 18 Измерить расстояние до недоступной точки.
Практические приложения подобия треугольников
Задача 5
180м
?
А
С
В
Из ∆АВС
∾ ∆А1В1С1
