- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Правильные многогранники
Содержание
- 1. Презентация по геометрии Правильные многогранники
- 2. Выпуклый многогранник называется правильным, если его грани
- 3. Историческая справкаО существовании пяти правильных многогранников знали
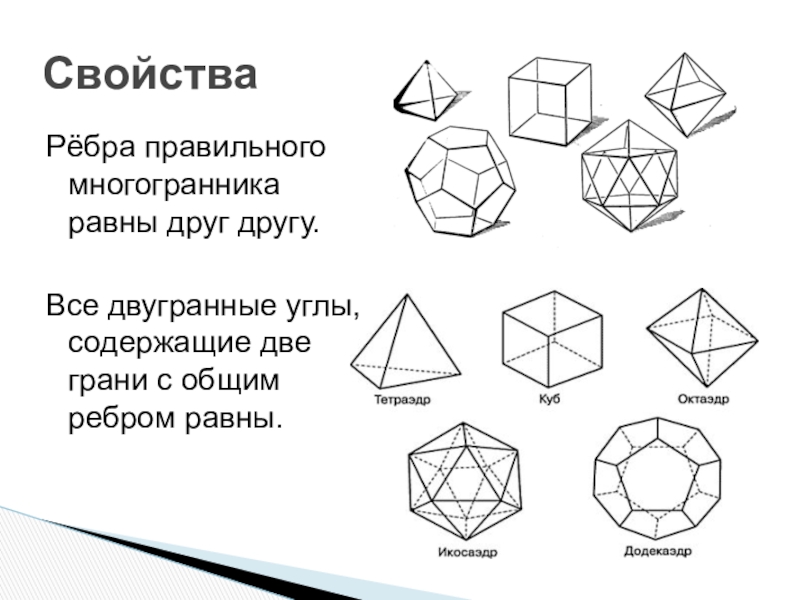
- 4. Рёбра правильного многогранника равны друг другу.Все двугранные углы, содержащие две грани с общим ребром равны.Свойства
- 5. ТеоремаНе существует правильного многогранника, гранями которого являются
- 6. По этой причине каждая вершина правильного многогранника
- 7. Существует 5 типов правильных многогранниковПравильный додекаэдрПравильный икосаэдрКубПравильный тетраэдрПравильный октаэдр
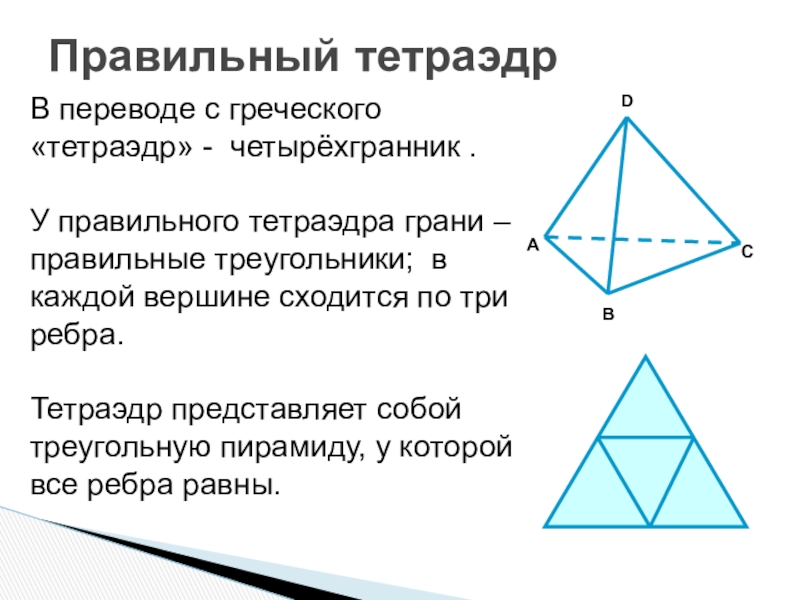
- 8. Правильный тетраэдрВ переводе с греческого «тетраэдр» -
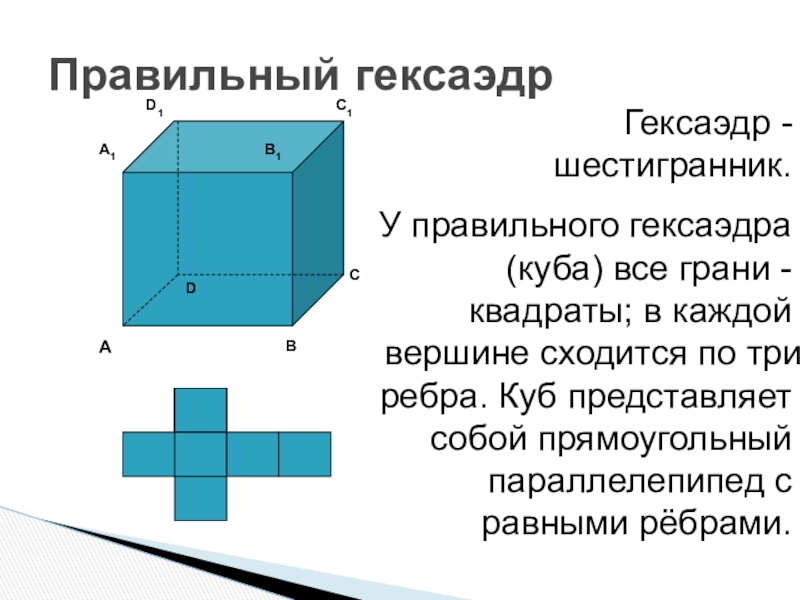
- 9. Правильный гексаэдрГексаэдр - шестигранник.У правильного гексаэдра (куба)
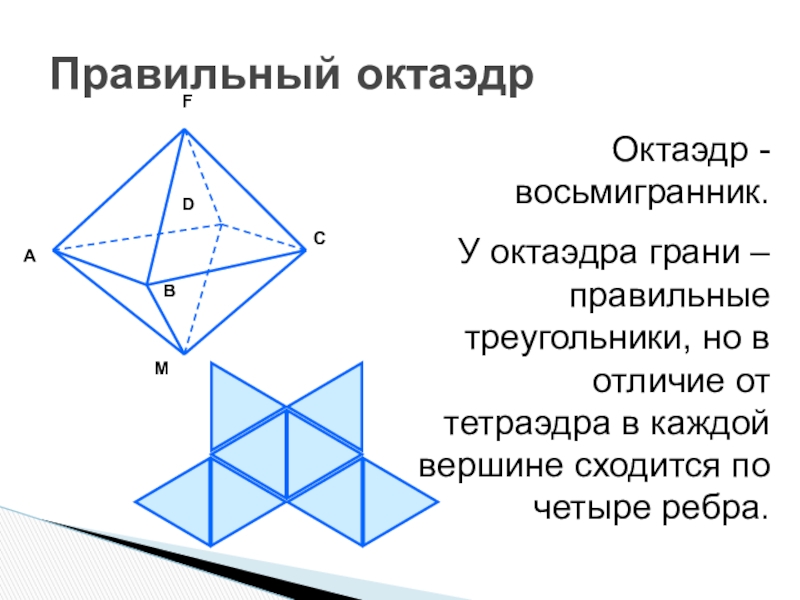
- 10. Правильный октаэдрОктаэдр - восьмигранник.У октаэдра грани –
- 11. Правильный додекаэдрДодекаэдр - двенадцатигранник.У додекаэдра грани – правильные пятиугольники. В каждой вершине сходится по три ребра.
- 12. Правильный икосаэдрИкосаэдр - двадцатигранник.У икосаэдра грани – правильные треугольники. В каждой вершине сходится по пять рёбер.
- 13. Названия многогранников Названия пришли из Древней Греции.В них указывается число граней:«эдра»-грань;«тетра»-4«гекса»-6«окта»-8«икоса»-20«додека»-12
- 14. Замечание:
- 15. Правильный тетраэдр не имеет центра симметрии;Правильный тетраэдр
Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число ребер.Определение правильного многогранника
Слайд 2Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с
одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число ребер.
Определение правильного многогранника
Слайд 3Историческая справка
О существовании пяти правильных многогранников знали еще в Древней Греции.
Великий древнегреческий мыслитель Платон считал, что четыре из них олицетворяют четыре «стихии»: тетраэдр – огонь, куб – землю, икосаэдр – воду, октаэдр – воздух. Пятый же многогранник, додекаэдр, символизировал собой все мироздание, представлял собой образ всей Вселенной, почитался главнейшим и его стали называть quinta essentia (квинта эссенциа») или «пятая сущность».
Правильные многогранники называют иногда Платоновыми телами, им посвящена последняя книга «Начал» Евклида. Её считают венцом стереометрии у древних греков.
Правильные многогранники называют иногда Платоновыми телами, им посвящена последняя книга «Начал» Евклида. Её считают венцом стереометрии у древних греков.
Слайд 4Рёбра правильного многогранника равны друг другу.
Все двугранные углы, содержащие две грани
с общим ребром равны.
Свойства
Слайд 5Теорема
Не существует правильного многогранника, гранями которого являются правильные n-угольники при n≥6.
Угол
правильного n-угольника при n≥6 не меньше 120.
При каждой вершине многогранника должно быть не менее 3 плоских углов, поэтому если бы существовал правильный многогранник, у которого все грани-правильные n-угольники при n≥6 , то сумма углов при каждой вершине такого многогранника была бы не меньше 360°(120°×3=360°), но это невозможно, т.к. сумма всех плоских углов при каждой вершине выпуклого многогранника меньше 360°.
При каждой вершине многогранника должно быть не менее 3 плоских углов, поэтому если бы существовал правильный многогранник, у которого все грани-правильные n-угольники при n≥6 , то сумма углов при каждой вершине такого многогранника была бы не меньше 360°(120°×3=360°), но это невозможно, т.к. сумма всех плоских углов при каждой вершине выпуклого многогранника меньше 360°.
Слайд 6По этой причине каждая вершина правильного многогранника может быть вершиной 3,
4 или 5 равносторонних треугольников, квадратов , правильных пятиугольников.
Слайд 7Существует 5 типов правильных многогранников
Правильный додекаэдр
Правильный икосаэдр
Куб
Правильный тетраэдр
Правильный октаэдр
Слайд 8Правильный тетраэдр
В переводе с греческого «тетраэдр» - четырёхгранник .
У правильного тетраэдра грани – правильные треугольники; в каждой вершине сходится по три ребра.
Тетраэдр представляет собой треугольную пирамиду, у которой все ребра равны.
С
Слайд 9Правильный гексаэдр
Гексаэдр - шестигранник.
У правильного гексаэдра (куба) все грани -квадраты; в
каждой вершине сходится по три ребра. Куб представляет собой прямоугольный параллелепипед с равными рёбрами.
Слайд 10Правильный октаэдр
Октаэдр - восьмигранник.
У октаэдра грани – правильные треугольники, но в
отличие от тетраэдра в каждой вершине сходится по четыре ребра.
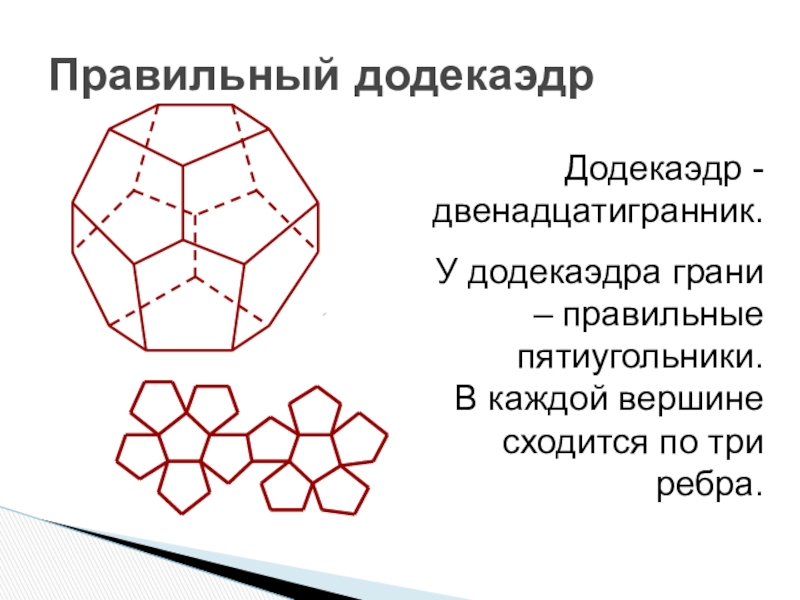
Слайд 11Правильный додекаэдр
Додекаэдр - двенадцатигранник.
У додекаэдра грани – правильные пятиугольники.
В каждой
вершине сходится по три ребра.
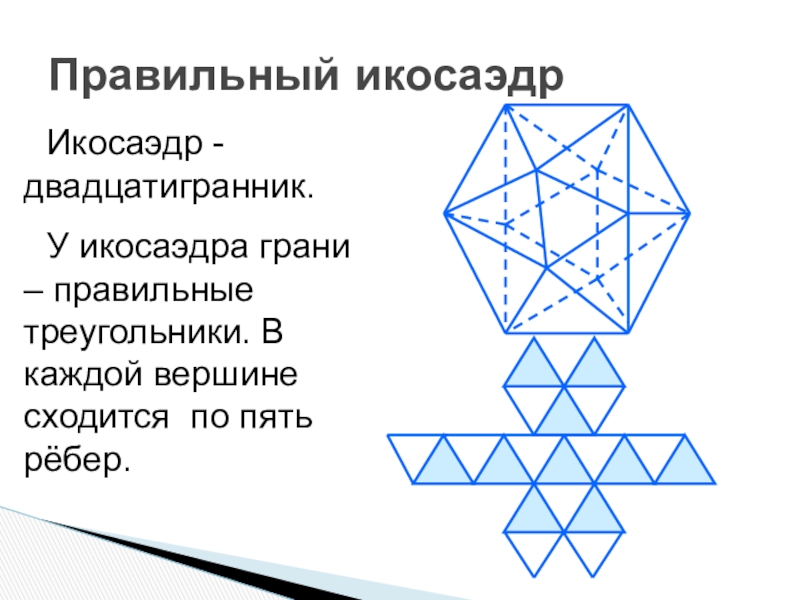
Слайд 12Правильный икосаэдр
Икосаэдр - двадцатигранник.
У икосаэдра грани – правильные треугольники. В каждой
вершине сходится по пять рёбер.
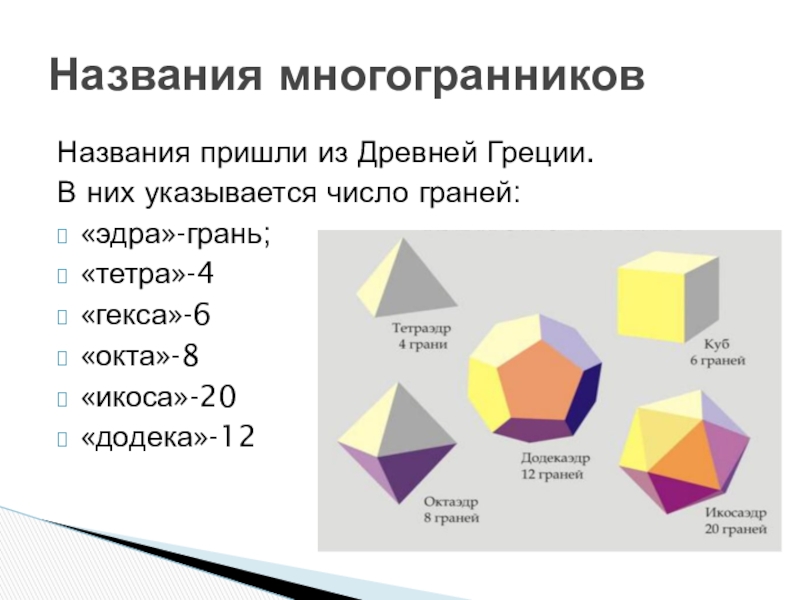
Слайд 13Названия многогранников
Названия пришли из Древней Греции.
В них указывается число граней:
«эдра»-грань;
«тетра»-4
«гекса»-6
«окта»-8
«икоса»-20
«додека»-12
Слайд 15Правильный тетраэдр не имеет центра симметрии;
Правильный тетраэдр имеет три оси симметрии
и шесть плоскостей симметрии;
Куб имеет один центр симметрии – точку пересечения его диагоналей;
Куб имеет девять осей симметрии;
Куб имеет девять плоскостей симметрии;
Правильный октаэдр, правильный икосаэдр и правильный додекаэдр имеют центр симметрии и несколько осей и плоскостей симметрии.
Куб имеет один центр симметрии – точку пересечения его диагоналей;
Куб имеет девять осей симметрии;
Куб имеет девять плоскостей симметрии;
Правильный октаэдр, правильный икосаэдр и правильный додекаэдр имеют центр симметрии и несколько осей и плоскостей симметрии.
Элементы симметрии правильных многогранников