- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Правильные многогранники
Содержание
- 1. Презентация по геометрии Правильные многогранники
- 2. Л.Кэрролл. «Правильных многогранников вызывающе мало, но этот
- 3. Еще в древней Греции были известны пять
- 4. ОпределениеМногогранник называется правильным, если все его грани
- 5. Платоновы телаДревнегреческий ученый и философ Платон (IV–V
- 6. Кубок КеплераИоганн Кеплер (1571-1630) в своей работе
- 7. Типы правильных многогранниковСуществуют пять типов правильных многогранников:тетраэдр
- 8. Правильный тетраэдрТетраэдр (tetra – четыре, hedra –
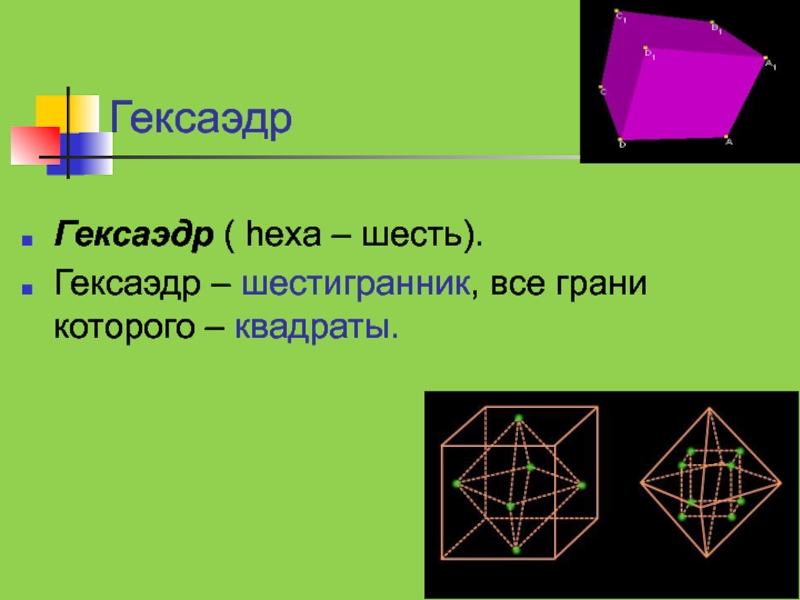
- 9. ГексаэдрГексаэдр ( hexa – шесть). Гексаэдр – шестигранник, все грани которого – квадраты.
- 10. ОктаэдрОктаэдр (okto – восемь). Октаэдр - восьмигранник, все грани которого – правильные треугольники.
- 11. ДодекаэдрДодекаэдр (dodeka – двенадцать) Додекаэдр - двенадцатигранник, все грани которого правильные пятиугольники.
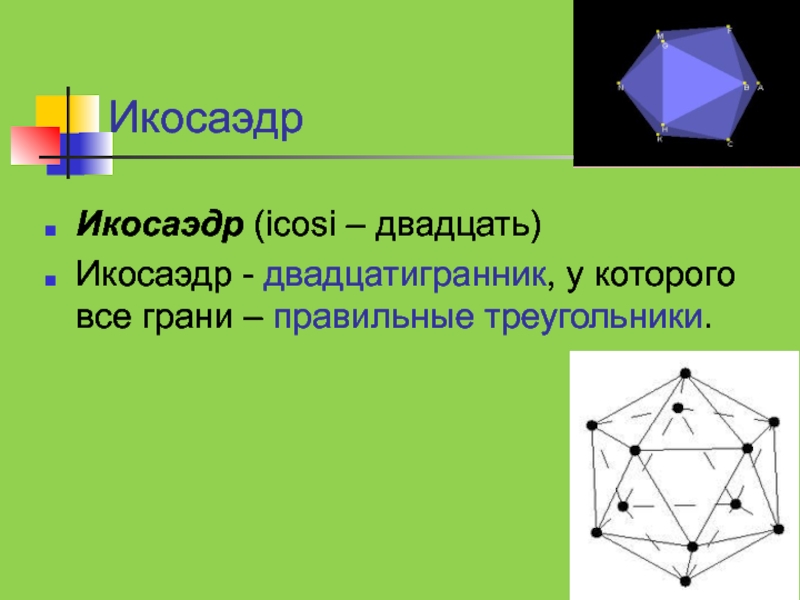
- 12. ИкосаэдрИкосаэдр (icosi – двадцать) Икосаэдр - двадцатигранник, у которого все грани – правильные треугольники.
- 13. Правильные многогранники в кристаллах В разных
- 14. Правильные многогранники в кристаллахКристаллы сернистого колчедана
- 15. Правильные многогранники в живой природе
- 16. Правильные многогранники в живой природе Вирус
- 17. Можно увидеть также, что молекула ДНК представляет
- 18. Решение задач
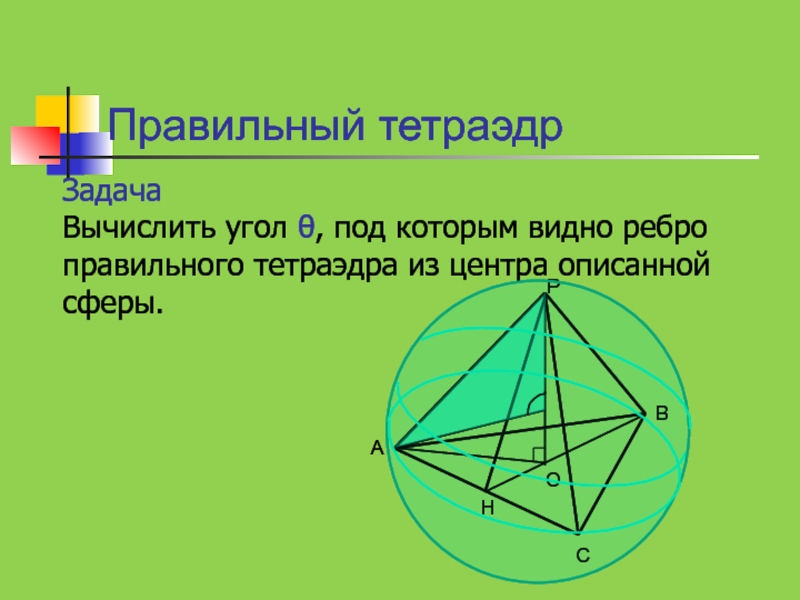
- 19. Правильный тетраэдрЗадача Вычислить угол θ, под которым видно ребро правильного тетраэдра из центра описанной сферы.
- 20. Задача 1.Рассмотрим правильный тетраэдр, ребро которого равно
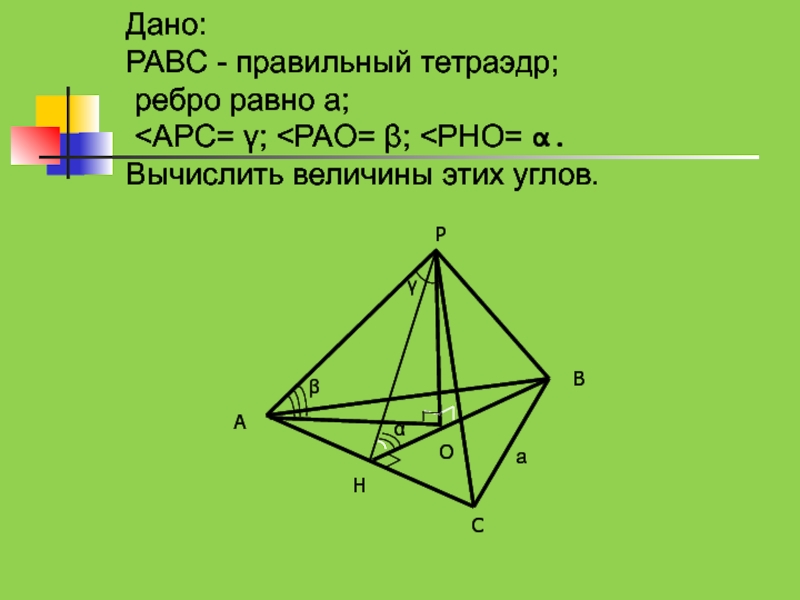
- 21. Дано: PABC - правильный тетраэдр; ребро равно а;
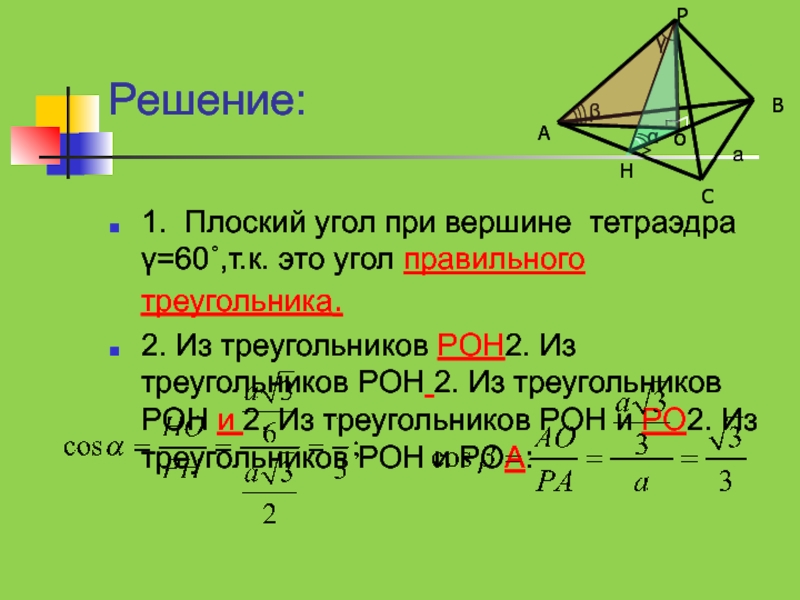
- 22. Решение:1. Плоский угол при вершине тетраэдра
- 23. Градусную меру угла можно вычислить с помощью инженерного калькулятора, округлив до нужной степени точности: α≈70,528ºβ≈54,735º
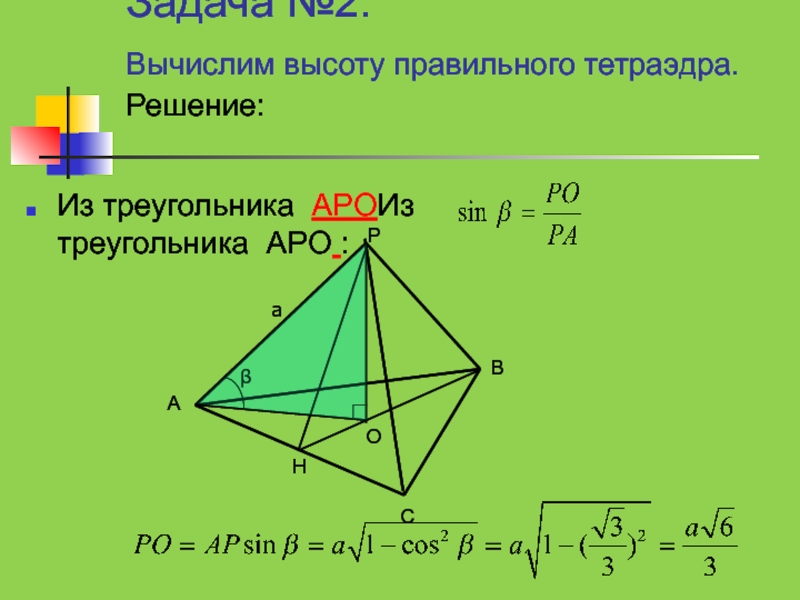
- 24. Задача №2. Вычислим высоту правильного тетраэдра.
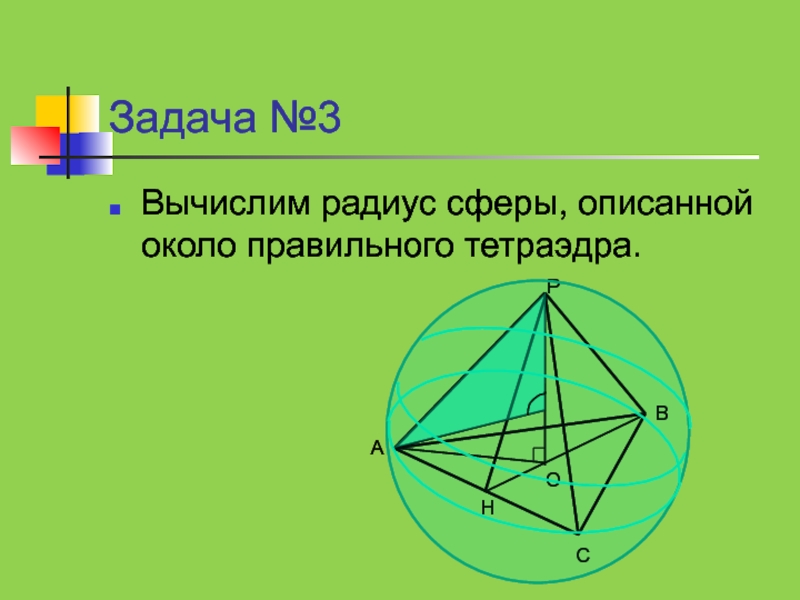
- 25. Задача №3Вычислим радиус сферы, описанной около правильного тетраэдра.
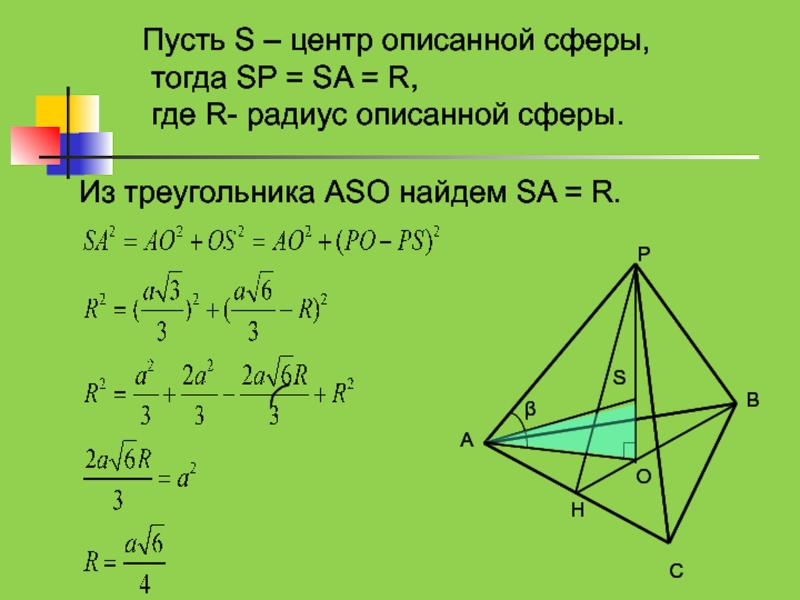
- 26. Пусть S – центр описанной сферы,
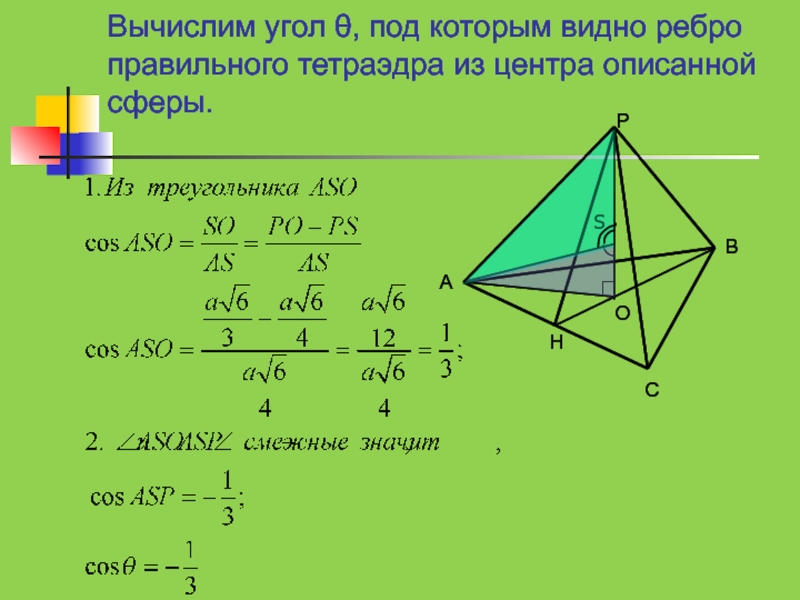
- 27. Вычислим угол θ, под которым видно ребро правильного тетраэдра из центра описанной сферы. S
- 28. Ответ: Дальше с помощью инженерного калькулятора вычисляем приближенное значение угла θ ≈ 109°27´.
- 29. Геометрия и химияЭта величина знакома нам из
Слайд 1Правильные многогранники
Выполнила
О.Б. Романько
преподаватель математики ГБПОУ СПбТК,
г. Санкт-Петербург
Слайд 2Л.Кэрролл.
«Правильных многогранников вызывающе мало,
но этот весьма скромный по численности
сумел пробраться в самые глубины различных наук».
Слайд 3 Еще в древней Греции были известны пять удивительных многогранников. Их изучали
Слайд 4Определение
Многогранник называется правильным, если
все его грани – равные между собой
из каждой его вершины выходит одинаковое число ребер ,
все двугранные углы равны.
http://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B0%D0%B2%D0%B8%D0%BB%D1%8C%D0%BD%D1%8B%D0%B9_%D0%BC%D0%BD%D0%BE%D0%B3%D0%BE%D0%B3%D1%80%D0%B0%D0%BD%D0%BD%D0%B8%D0%BA
Слайд 5Платоновы тела
Древнегреческий ученый и философ Платон (IV–V в до н. э.) считал,
Слайд 6Кубок Кеплера
Иоганн Кеплер (1571-1630) в своей работе "Тайна мироздания" в 1596
Слайд 7Типы правильных многогранников
Существуют пять типов правильных многогранников:
тетраэдр
гексаэдр
октаэдр
додекаэдр
икосаэдр
Можно доказать, что других правильных многогранников не существует.
http://polyhedron2008.narod.ru/pages/polyhedr.ht
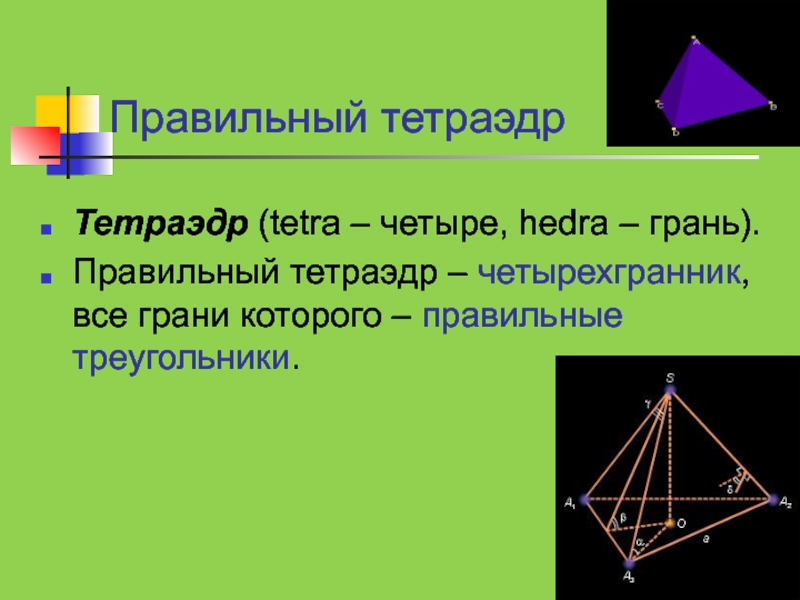
Слайд 8Правильный тетраэдр
Тетраэдр (tetra – четыре, hedra – грань).
Правильный тетраэдр –
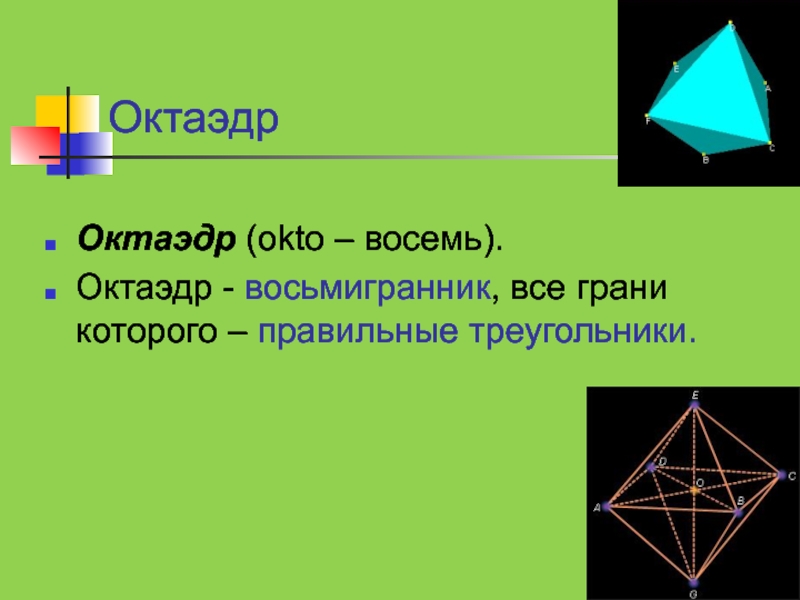
Слайд 10Октаэдр
Октаэдр (okto – восемь).
Октаэдр - восьмигранник, все грани которого –
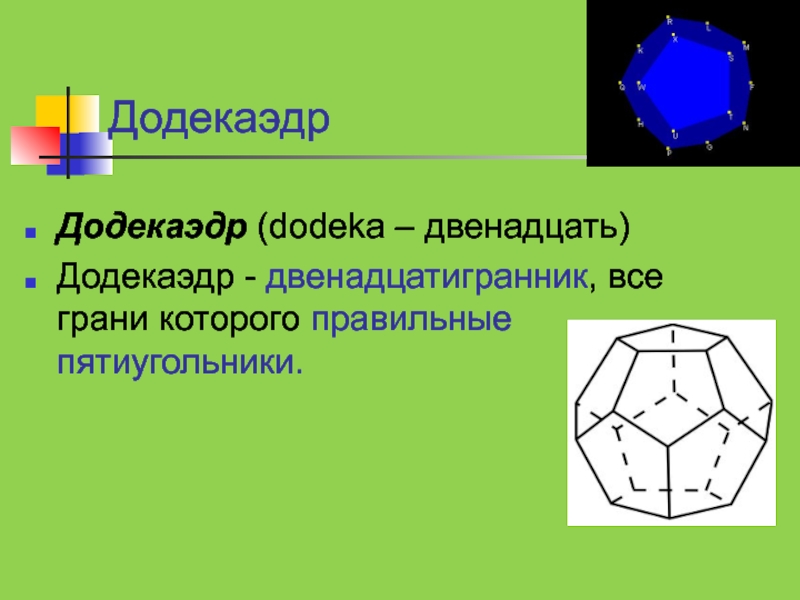
Слайд 11Додекаэдр
Додекаэдр (dodeka – двенадцать)
Додекаэдр - двенадцатигранник, все грани которого правильные
Слайд 12Икосаэдр
Икосаэдр (icosi – двадцать)
Икосаэдр - двадцатигранник, у которого все грани
Слайд 13Правильные многогранники
в кристаллах
В разных химических реакциях применяется сурьменистый сернокислый
Кристаллы поваренной соли имеют форму куба.
При производстве алюминия пользуются алюминиево-калиевыми кварцами , монокристалл которых имеет форму правильного октаэдра.
Слайд 14Правильные многогранники
в кристаллах
Кристаллы сернистого колчедана – пирита - имеют форму
Правильный многогранник – икосаэдр передаёт форму кристаллов бора.
Кристаллы алмаза представляют собой гигантские полимерные молекулы и обычно имеют форму октаэдров, ромбододекаэдров, реже — кубов или тетраэдров.
Слайд 15Правильные многогранники
в живой природе
Скелет одноклеточного организма феодарии по
Слайд 16Правильные многогранники
в живой природе
Вирус полиомиелита имеет форму додекаэдра. Он
Большинство вирусов имеют форму икосаэдра Только взяв на вооружение электронный микроскоп, биологам удалось сфотографировать вирусы и получить представление об их форме.
Слайд 17Можно увидеть также, что молекула ДНК представляет собой вращающийся куб. При
Правильные многогранники
в живой природе
Слайд 19Правильный тетраэдр
Задача
Вычислить угол θ, под которым видно ребро правильного тетраэдра
Слайд 20Задача 1.
Рассмотрим правильный тетраэдр, ребро которого равно а, плоский угол при
Слайд 22Решение:
1. Плоский угол при вершине тетраэдра γ=60˚,т.к. это
2. Из треугольников POH2. Из треугольников POH 2. Из треугольников POH и 2. Из треугольников POH и PO2. Из треугольников POH и POА:
o
γ
Слайд 23Градусную меру угла можно вычислить с помощью инженерного калькулятора, округлив до
α≈70,528º
β≈54,735º
Слайд 24Задача №2. Вычислим высоту правильного тетраэдра.
Из треугольника APOИз треугольника APO :
А
В
С
О
Н
Р
β
a
Слайд 26Пусть S – центр описанной сферы, тогда SP = SA =
Из треугольника ASO найдем SA = R.
С