г. Сургут
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Повторение. Часть 2. Треугольники, подобие (8 класс )
Содержание
- 1. Презентация по геометрии Повторение. Часть 2. Треугольники, подобие (8 класс )
- 2. Повторяем теориюЧто такое треугольник? Треугольник –это геометрическая фигура,
- 3. Повторяем теориюДавайте остановимся подробнее на прямоугольном треугольнике.900Сформулируйте
- 4. Повторяем теориюВАДля успешного решения задач мы должны
- 5. Повторяем теориюВАВспомним три признака равенства треугольников СПо
- 6. Повторяем теориюВАВспомним три признака равенства треугольников СПо
- 7. Треугольники называются подобными, если их стороны пропорциональны.Повторяем
- 8. Сформулируйте второй признак подобия треугольниковПовторяем теориюВАСдве стороны
- 9. Повторяем теориюВАСтри стороны одного треугольника пропорциональны трем
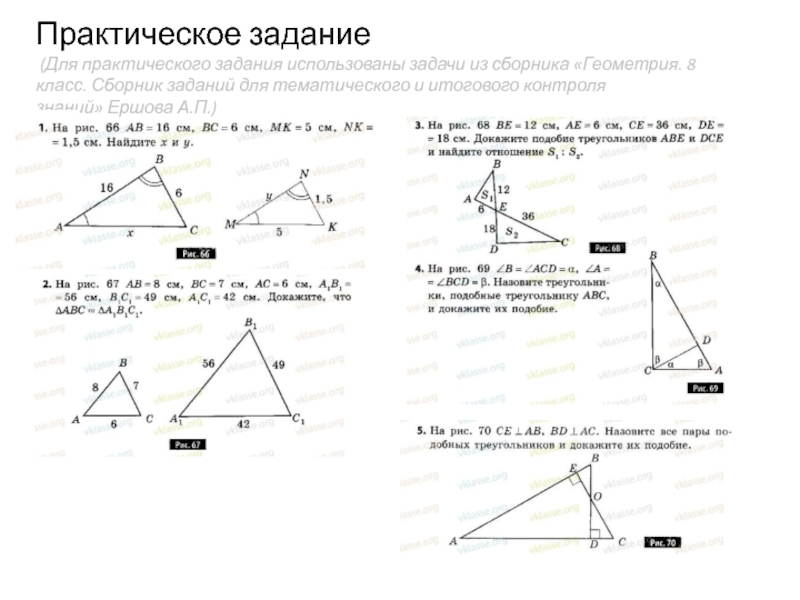
- 10. Практическое задание (Для практического задания использованы
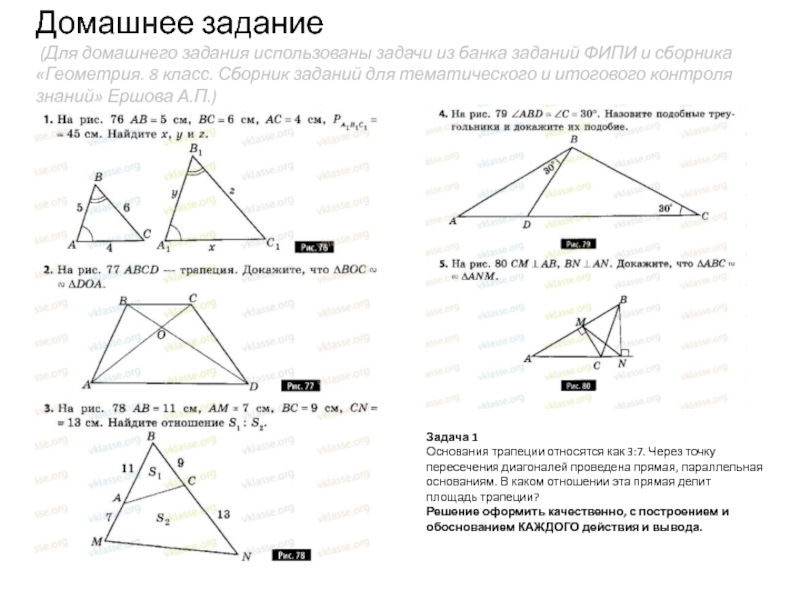
- 11. Домашнее задание (Для домашнего задания использованы
Повторяем теориюЧто такое треугольник? Треугольник –это геометрическая фигура, которая состоит из трех точек, соединенных отрезкамиВАНазовитеКакие треугольники вы знаете?остроугольныйС900А,В,С -вершины треугольникарис. 1-стороны треугольникаАВ,ВС,СА -углы треугольникаСАВ, АВС, ВСА иначе А, В, С тупоугольныйпрямоугольныйразностороннийравнобедренныйравностороннийрис. 2АВСрис.
Слайд 2Повторяем теорию
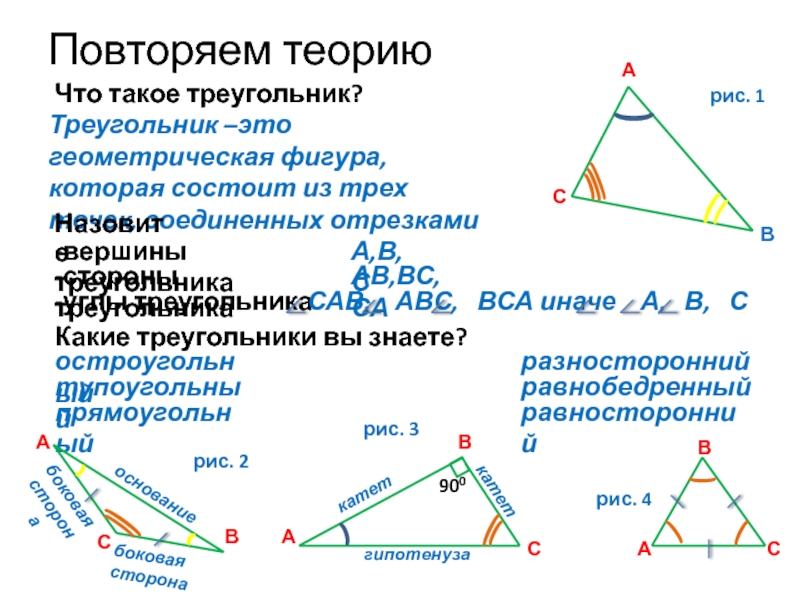
Что такое треугольник?
Треугольник –это геометрическая фигура, которая состоит из трех
точек, соединенных отрезками
В
А
Назовите
Какие треугольники вы знаете?
остроугольный
С
900
А,В,С
-вершины треугольника
рис. 1
-стороны треугольника
АВ,ВС,СА
-углы треугольника
САВ, АВС, ВСА иначе А, В, С
тупоугольный
прямоугольный
разносторонний
равнобедренный
равносторонний
рис. 2
А
В
С
рис. 3
основание
боковая сторона
боковая
сторона
катет
катет
гипотенуза
А
В
С
рис. 4
А
В
С
Слайд 3Повторяем теорию
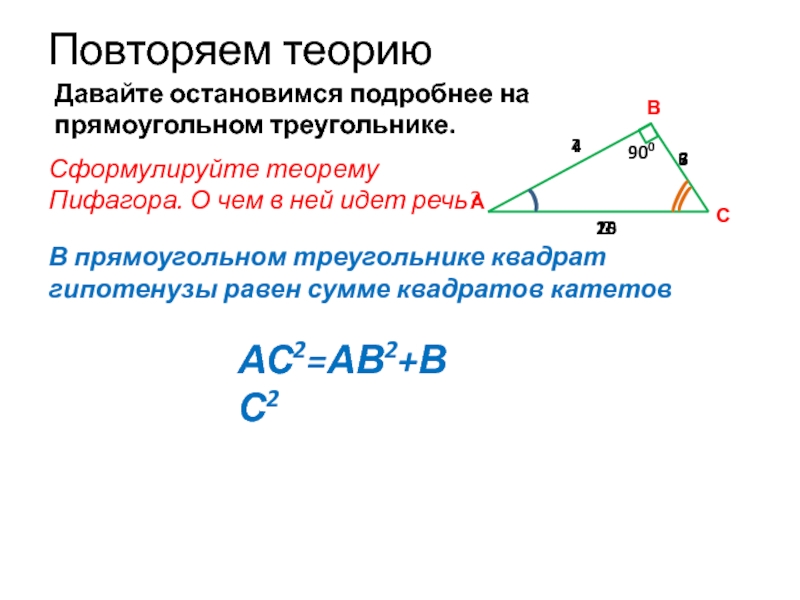
Давайте остановимся подробнее на прямоугольном треугольнике.
900
Сформулируйте теорему Пифагора. О чем
в ней идет речь?
А
В
С
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
АС2=АВ2+ВС2
25
10
6
?
4
3
?
7
?
Слайд 4Повторяем теорию
В
А
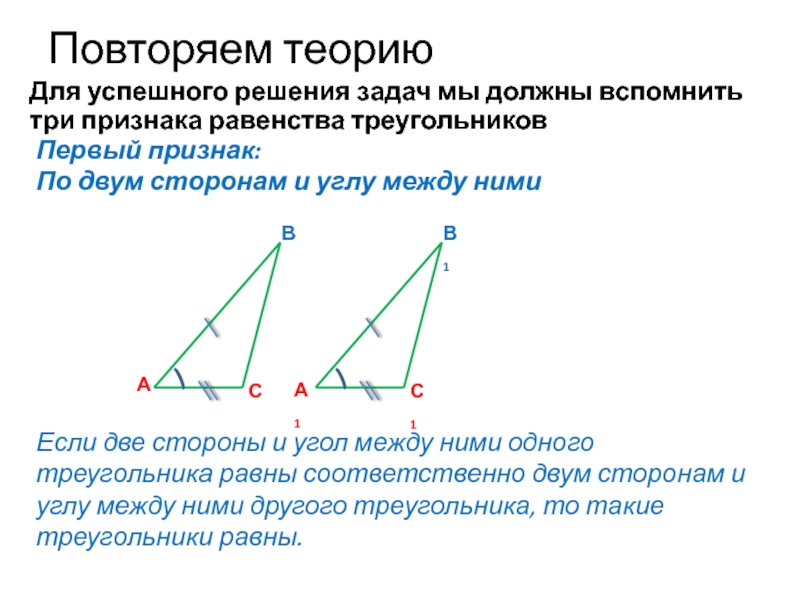
Для успешного решения задач мы должны вспомнить три признака равенства
треугольников
С
Первый признак:
Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
В1
А1
С1
По двум сторонам и углу между ними
Слайд 5Повторяем теорию
В
А
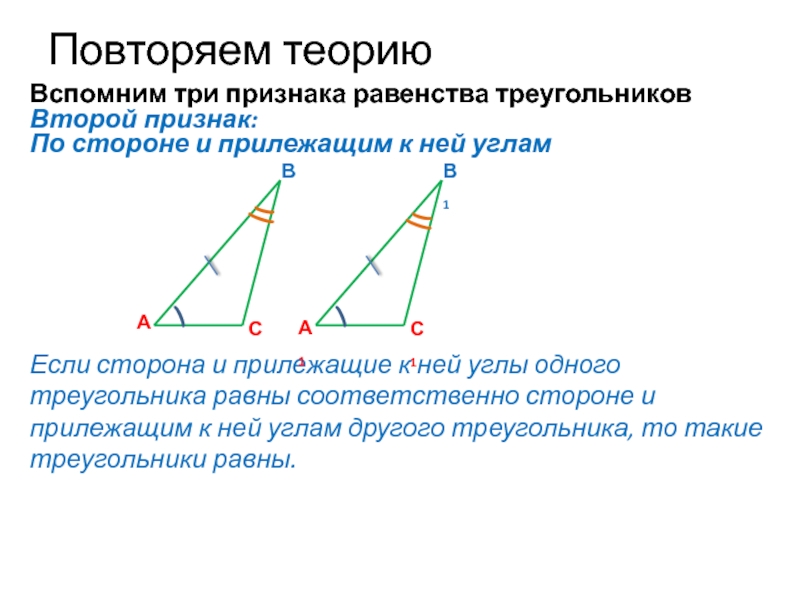
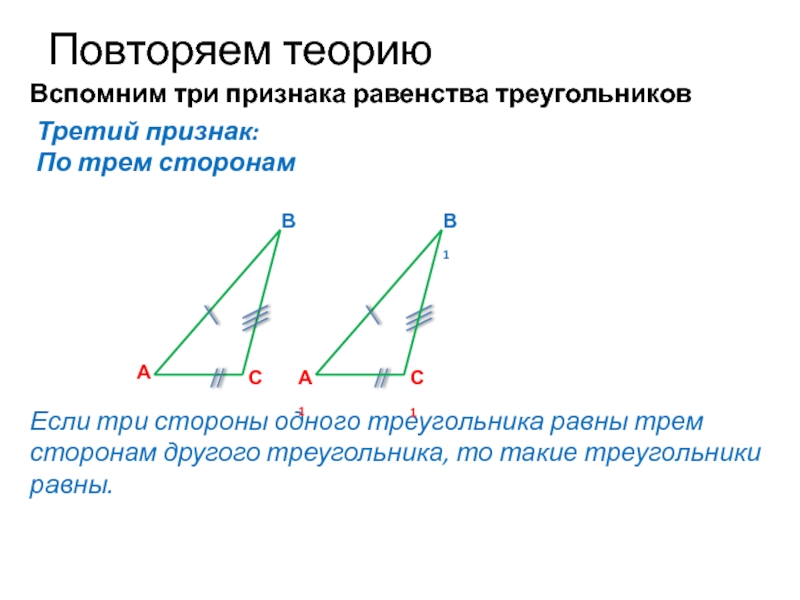
Вспомним три признака равенства треугольников
С
По стороне и прилежащим к
ней углам
Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
В1
А1
С1
Второй признак:
Слайд 6Повторяем теорию
В
А
Вспомним три признака равенства треугольников
С
По трем сторонам
Если три стороны
одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.
В1
А1
С1
Третий признак:
Слайд 7Треугольники называются подобными, если их стороны пропорциональны.
Повторяем теорию
В
А
Вспомним три признака подобия
треугольников
С
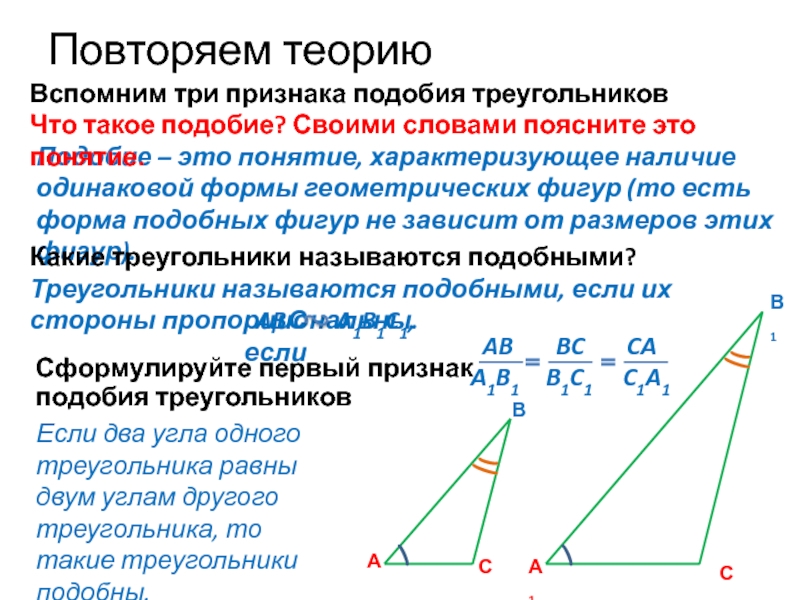
Подобие – это понятие, характеризующее наличие одинаковой формы геометрических фигур (то есть форма подобных фигур не зависит от размеров этих фигур).
Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
В1
А1
С1
Что такое подобие? Своими словами поясните это понятие.
Сформулируйте первый признак подобия треугольников
AB BC CA
A1B1 B1C1 C1A1
ABС A1B1C1, если
Какие треугольники называются подобными?
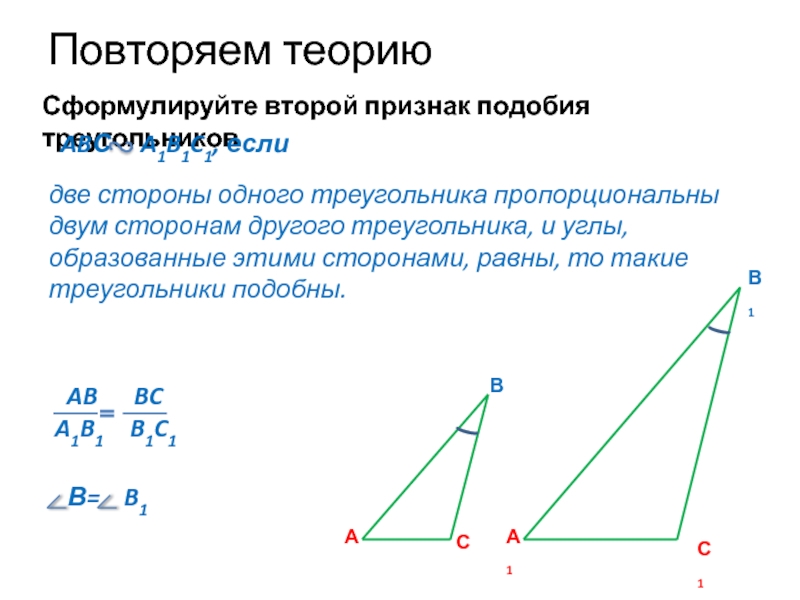
Слайд 8Сформулируйте второй признак подобия треугольников
Повторяем теорию
В
А
С
две стороны одного треугольника пропорциональны двум
сторонам другого треугольника, и углы, образованные этими сторонами, равны, то такие треугольники подобны.
В1
А1
С1
AB BC
A1B1 B1C1
ABС A1B1C1, если
В= B1
Слайд 9Повторяем теорию
В
А
С
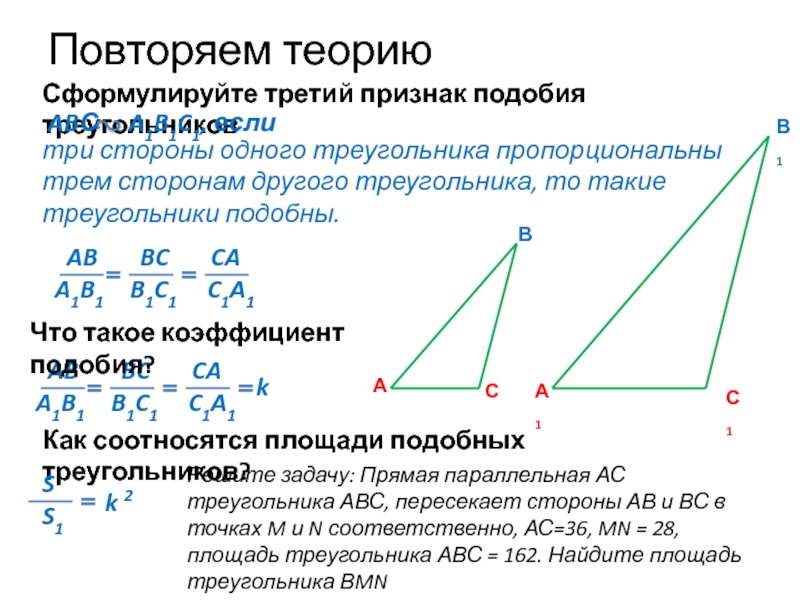
три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то
такие треугольники подобны.
В1
А1
С1
Сформулируйте третий признак подобия треугольников
ABС A1B1C1, если
AB BC CA
A1B1 B1C1 C1A1
AB BC CA
A1B1 B1C1 C1A1
Что такое коэффициент подобия?
k
Как соотносятся площади подобных треугольников?
S
S1
k 2
Решите задачу: Прямая параллельная АС треугольника АВС, пересекает стороны АВ и ВС в точках M и N соответственно, АС=36, MN = 28, площадь треугольника АВС = 162. Найдите площадь треугольника ВMN
Слайд 10Практическое задание (Для практического задания использованы задачи из сборника «Геометрия. 8
класс. Сборник заданий для тематического и итогового контроля знаний» Ершова А.П.)
Слайд 11Домашнее задание (Для домашнего задания использованы задачи из банка заданий ФИПИ
и сборника «Геометрия. 8 класс. Сборник заданий для тематического и итогового контроля знаний» Ершова А.П.)
)
Задача 1
Основания трапеции относятся как 3:7. Через точку пересечения диагоналей проведена прямая, параллельная основаниям. В каком отношении эта прямая делит площадь трапеции?
Решение оформить качественно, с построением и обоснованием КАЖДОГО действия и вывода.
