не усвоил ничего нового и ничего не прибавил к своему образованию».
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии по теме Касательная к окружности (8 класс)
Содержание
- 1. Презентация по геометрии по теме Касательная к окружности (8 класс)
- 2. Как вы думаете, сколько общих точек могут иметь прямая и окружность?О
- 3. Тема урока «Касательная к окружности»
- 4. Цель урокаРассмотреть различные случаи взаимного расположения прямой и плоскости, Ввести понятие касательной к окружности
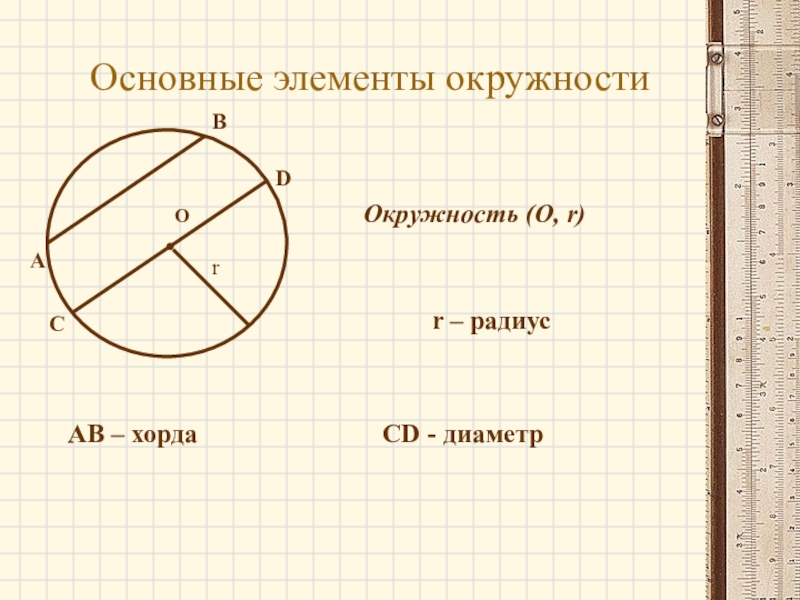
- 5. ООсновные элементы окружностиОкружность (О, r)r – радиусrABАВ – хорда СDCD - диаметр
- 6. ОРадиус окружности равен 5 см. Найдите расстояние
- 7. ОНайдите расстояние от точки А до ближайшей
- 8. ОНайдите расстояние от точки А до ближайшей
- 9. Исследуем взаимное расположение прямой и окружности в
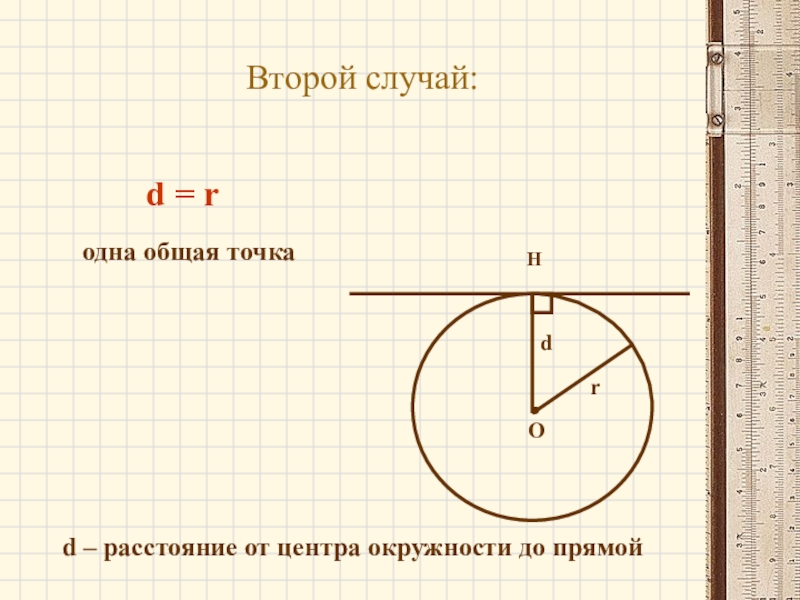
- 10. Второй случай:ОНrодна общая точкаd = rd – расстояние от центра окружности до прямойd
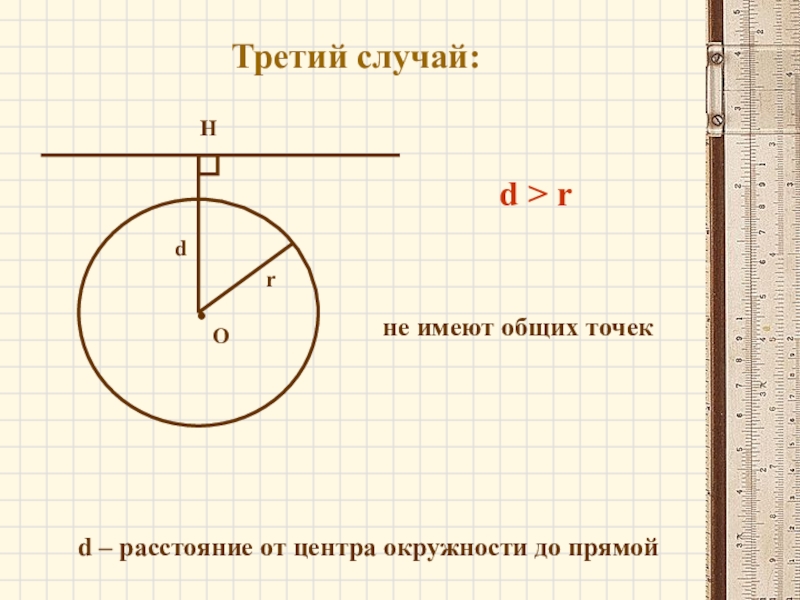
- 11. Третий случай:ОHdrd > rd – расстояние от центра окружности до прямойне имеют общих точек
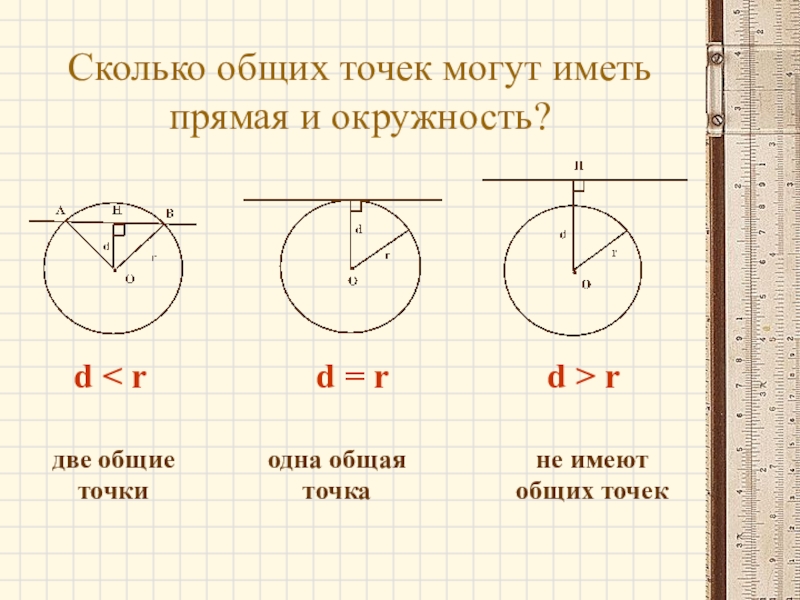
- 12. Сколько общих точек могут иметь прямая и
- 13. Взаимное расположение прямой и окружностиrd = rОкружность
- 14. Свойство касательной.Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. АВ
- 15. 600
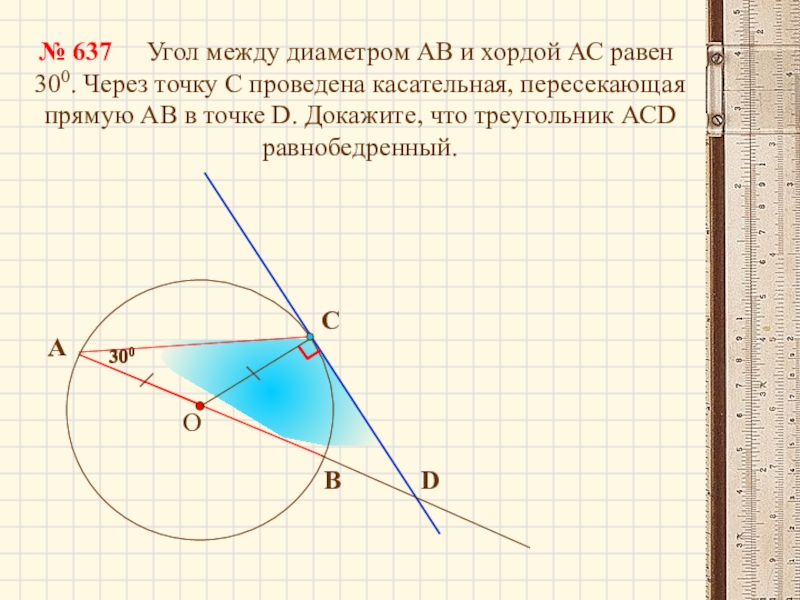
- 16. 300
- 17. Решите задачу В треугольнике АВС угол
- 18. Подготовка к ОГЭ (задание №20)Выберите верное утверждение:
- 19. Проверь себяВыберите верное утверждение: 1)Если расстояние от
- 20. Домашнее задание: П.70, 71 №636, 633. Дополнительно:
- 21. Слайд 21
Как вы думаете, сколько общих точек могут иметь прямая и окружность?О
Слайд 4Цель урока
Рассмотреть различные случаи взаимного расположения прямой и плоскости,
Ввести понятие
касательной к окружности
Слайд 6
О
Радиус окружности равен 5 см. Найдите расстояние от центра окружности до
прямой, содержащей хорду, равную 8 см.
Окружность (О, 5)
5
A
B
Н
5
Слайд 7
О
Найдите расстояние от точки А до ближайшей к неё точки окружности
с центром О радиуса r, если а) ОА = 12см,
r = 8 см.
Окружность (О, 8)
A
Н
Слайд 8
О
Найдите расстояние от точки А до ближайшей к неё точки окружности
с центром О радиуса r, если а) ОА = 6см,
r = 8 см.
Окружность (О, 8)
A
Н
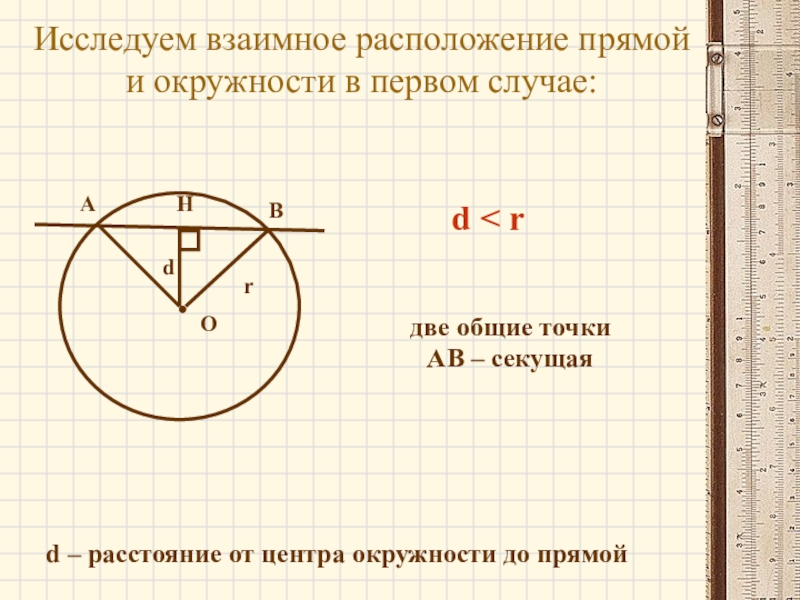
Слайд 9Исследуем взаимное расположение прямой и окружности в первом случае:
d – расстояние
от центра окружности до прямой
О
А
В
Н
d < r
две общие точки
АВ – секущая
r
d
Слайд 12Сколько общих точек могут иметь прямая и окружность?
d < r
d
= r
d > r
две общие точки
одна общая точка
не имеют общих точек
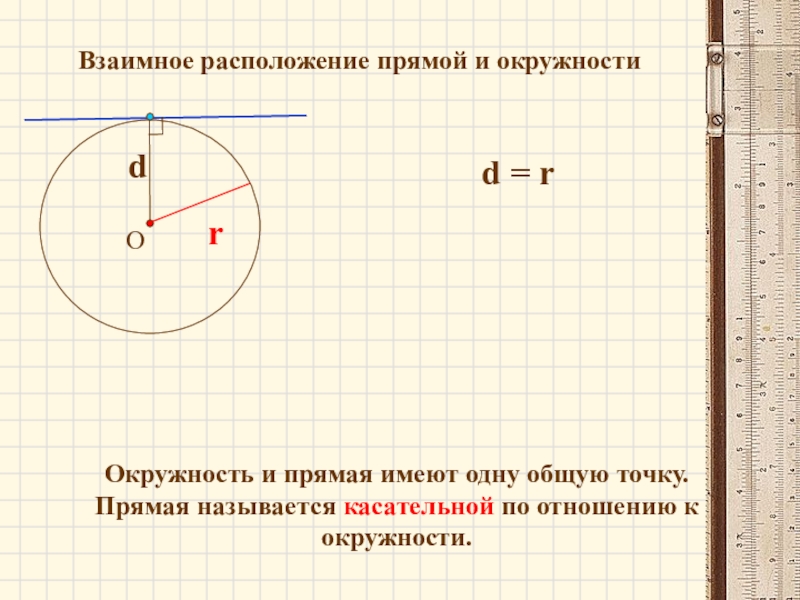
Слайд 13
Взаимное расположение прямой и окружности
r
d = r
Окружность и прямая имеют одну
общую точку.
Прямая называется касательной по отношению к окружности.
Прямая называется касательной по отношению к окружности.
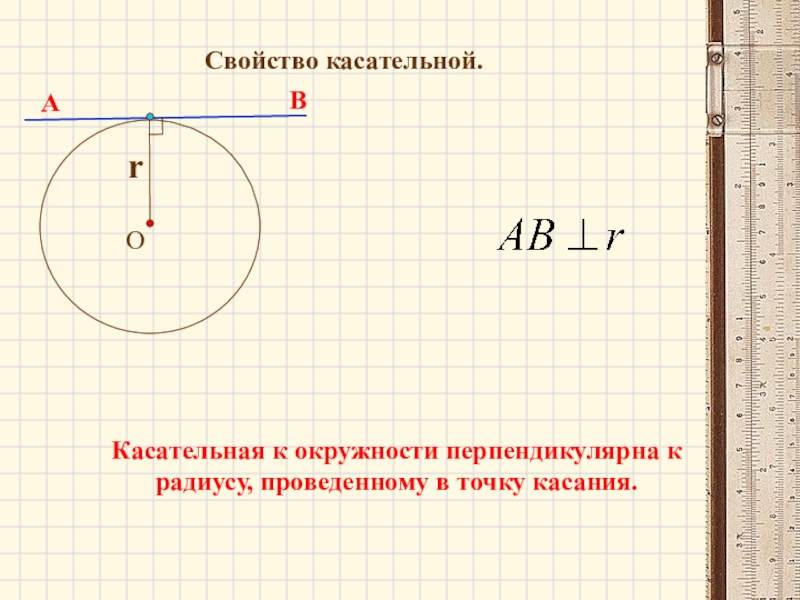
Слайд 14
Свойство касательной.
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
А
В
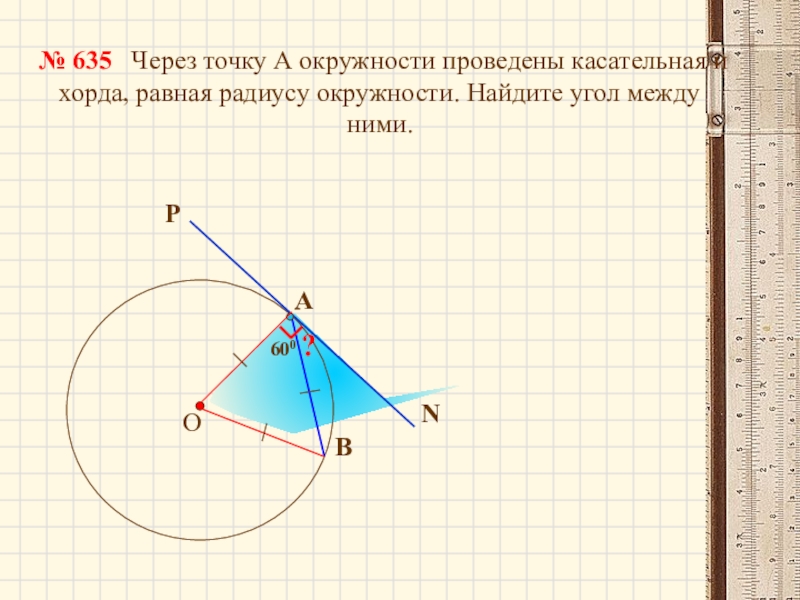
Слайд 15
600
Через точку А
окружности проведены касательная и хорда, равная радиусу окружности. Найдите угол между ними.
№ 635
?
Слайд 16
300
Угол между
диаметром АВ и хордой АС равен 300. Через точку С проведена касательная, пересекающая прямую АВ в точке D. Докажите, что треугольник АСD равнобедренный.
№ 637
300
Слайд 17Решите задачу
В треугольнике АВС угол А равен 90 градусов,
АВ = 5см, ВС= 13 см. Найдите радиус окружности центром в точке С, если она имеет с прямой АВ одну общую точку.
Слайд 18Подготовка к ОГЭ (задание №20)
Выберите верное утверждение:
1)Если расстояние от центра
до прямой больше радиуса окружности, то окружность и прямая имеют две общие точки.
2) Если расстояние от центра до прямой равно радиусу окружности, то окружность и прямая имеют одну общую точку.
3) Если расстояние от центра до прямой меньше радиуса окружности, то окружность и прямая не имеют общих точек.
4) Прямая, имеющая с окружностью одну общую точку, называется касательной к окружности.
5) Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
2) Если расстояние от центра до прямой равно радиусу окружности, то окружность и прямая имеют одну общую точку.
3) Если расстояние от центра до прямой меньше радиуса окружности, то окружность и прямая не имеют общих точек.
4) Прямая, имеющая с окружностью одну общую точку, называется касательной к окружности.
5) Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Слайд 19Проверь себя
Выберите верное утверждение:
1)Если расстояние от центра до прямой больше
радиуса окружности, то окружность и прямая имеют две общие точки.
2) Если расстояние от центра до прямой равно радиусу окружности, то окружность и прямая имеют одну общую точку.
3) Если расстояние от центра до прямой меньше радиуса окружности, то окружность и прямая не имеют общих точек.
4) Прямая, имеющая с окружностью одну общую точку, называется касательной к окружности.
5) Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Ответ: 245
2) Если расстояние от центра до прямой равно радиусу окружности, то окружность и прямая имеют одну общую точку.
3) Если расстояние от центра до прямой меньше радиуса окружности, то окружность и прямая не имеют общих точек.
4) Прямая, имеющая с окружностью одну общую точку, называется касательной к окружности.
5) Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Ответ: 245
Слайд 20Домашнее задание:
П.70, 71
№636, 633.
Дополнительно: задача с сайта Гущина
№348602 (прототип №17)
Отрезок АВ = 32 см касается окружности радиуса 24 см с центром в точке О . Окружность пересекает отрезок ОА в точке К. Найдите АК.
Отрезок АВ = 32 см касается окружности радиуса 24 см с центром в точке О . Окружность пересекает отрезок ОА в точке К. Найдите АК.
