Составила учитель математики МБОУ «Красногвардейская школа№1»
Коваленко И.Н.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии по теме: Элементы симметрии правильных многогранников
Содержание
- 1. Презентация по геометрии по теме: Элементы симметрии правильных многогранников
- 2. Симметрия в пространстве. Элементы симметрии правильных многогранников
- 3. Толковый словарь русского языка В.И. Даля:СИММЕТРИЯ -
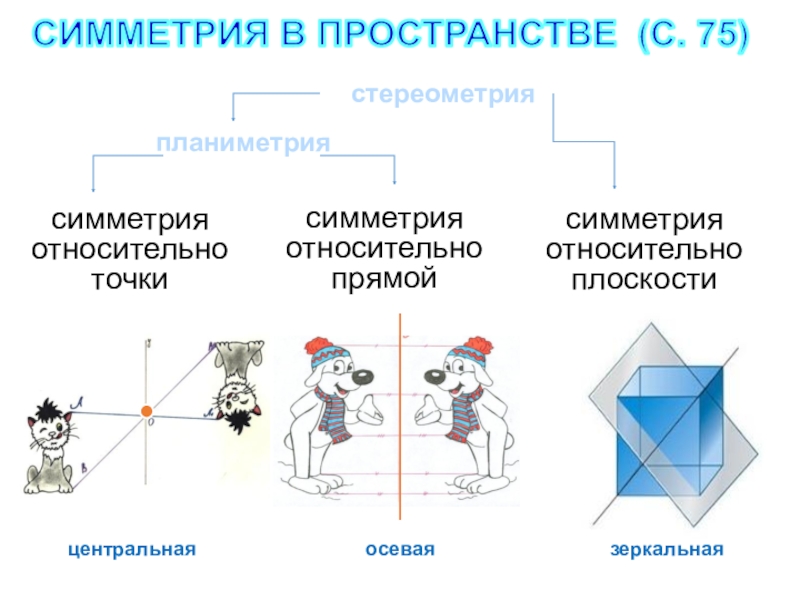
- 4. симметрия относительно точки симметрия относительно прямой симметрия относительно плоскости СИММЕТРИЯ В ПРОСТРАНСТВЕ (С. 75)планиметриястереометрияцентральнаяосеваязеркальная
- 5. СИММЕТРИЯ В ПРОСТРАНСТВЕТочки А и А1 называются
- 6. СИММЕТРИЯ В ПРОСТРАНСТВЕТочки А и А1 называются
- 7. СИММЕТРИЯ В ПРОСТРАНСТВЕТочки А и А1 называются
- 8. Центр симметрииПлоскость симметрииТочка (прямая, плоскость) называется центром
- 9. СИММЕТРИЯ В ФИЗИКЕ И ТЕХНИКЕВзаимосвязь электрического
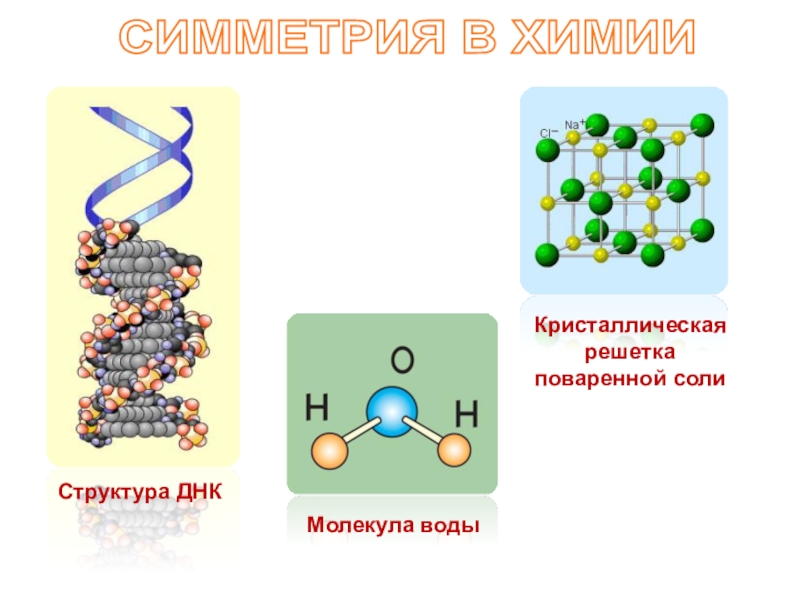
- 10. СИММЕТРИЯ В ХИМИИКристаллическая решетка поваренной солиМолекула водыСтруктура ДНК
- 11. СИММЕТРИЯ В БИОЛОГИИ (биосимметрика)
- 12. СИММЕТРИЯ В АРХИТЕКТУРЕЦерковь Покрова БогородицыЗдание МГУ в МосквеБольшой дворец в СтрельнеКонстантиновский дворец
- 13. СИММЕТРИЯ В АРХИТЕКТУРЕ
- 14. СИММЕТРИЯ В ИСКУССТВЕСальвадор Дали «Тайная вечеря»Микеланджело Гробница Джулиано Медичи
- 15. Обладает ли симметрией лицо человека?
- 16. Эпиграф «Правильных многогранников вызывающе мало, но этот
- 17. Многогранник – поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело.
- 18. Выпуклый многогранник называется правильным, если все его
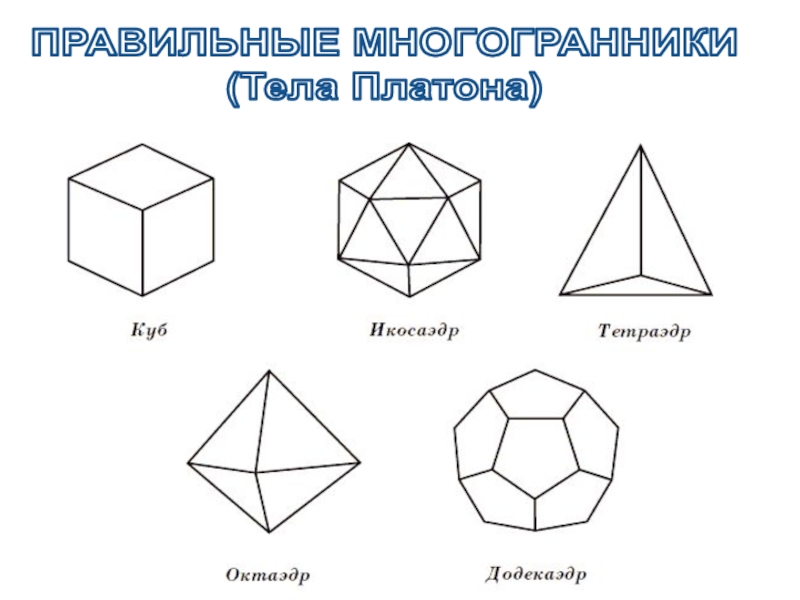
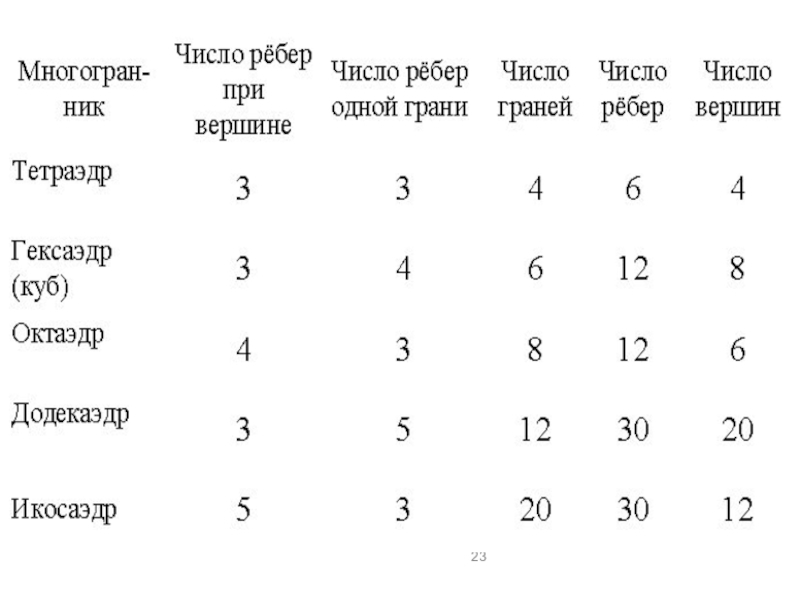
- 19. Существует пять типов правильных выпуклых многогранников: правильный тетраэдр, куб, октаэдр, додекаэдр, икосаэдр
- 20. ПРАВИЛЬНЫЕ МНОГОГРАННИКИ (Тела Платона)
- 21. Названия многогранников Пришли из Древней Греции, в
- 22. ТетраэдрИкосаэдрГексаэдрДодекаэдрОктаэдр
- 23. Слайд 23
- 24. Большой звездчатыйдодекаэдрБольшой икосаэдрМалый звездчатыйдодекаэдрБольшой додекаэдр
- 25. Правильные многогранники иногда
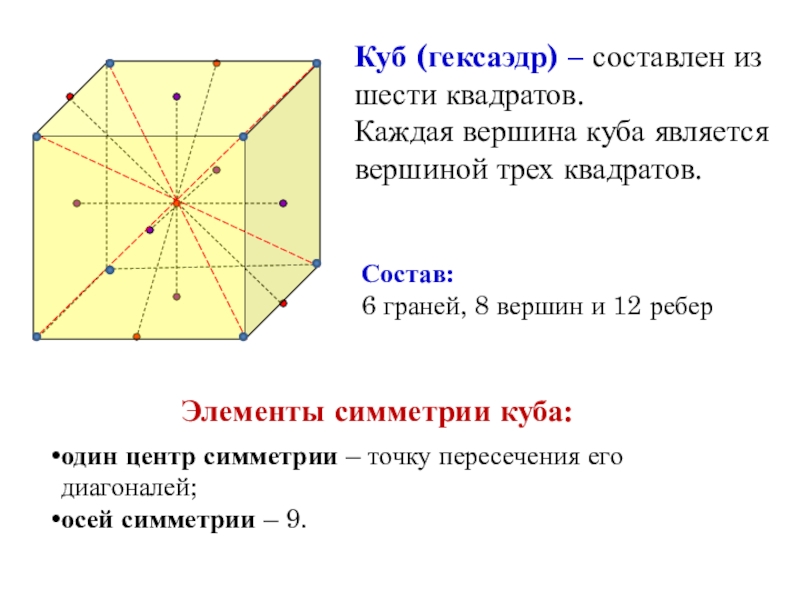
- 26. Куб (гексаэдр) – составлен из шести квадратов.
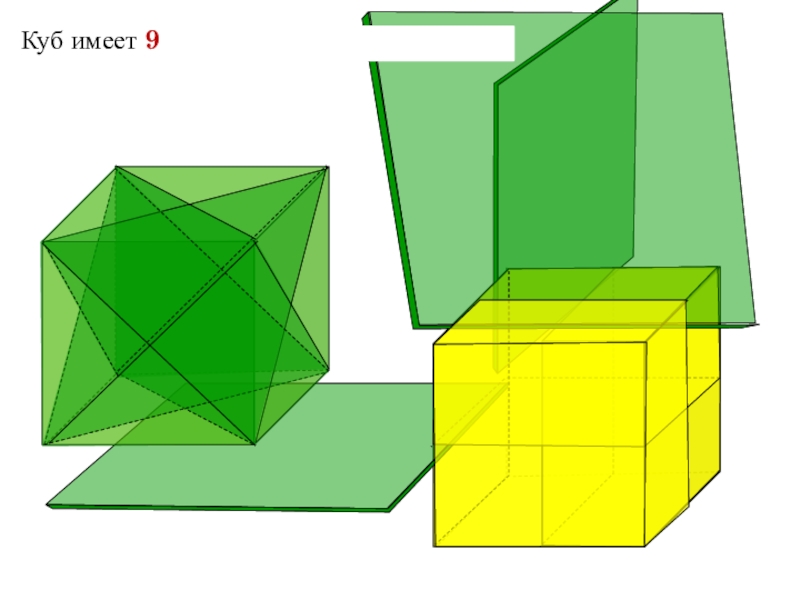
- 27. Куб имеет 9 плоскостей симметрии
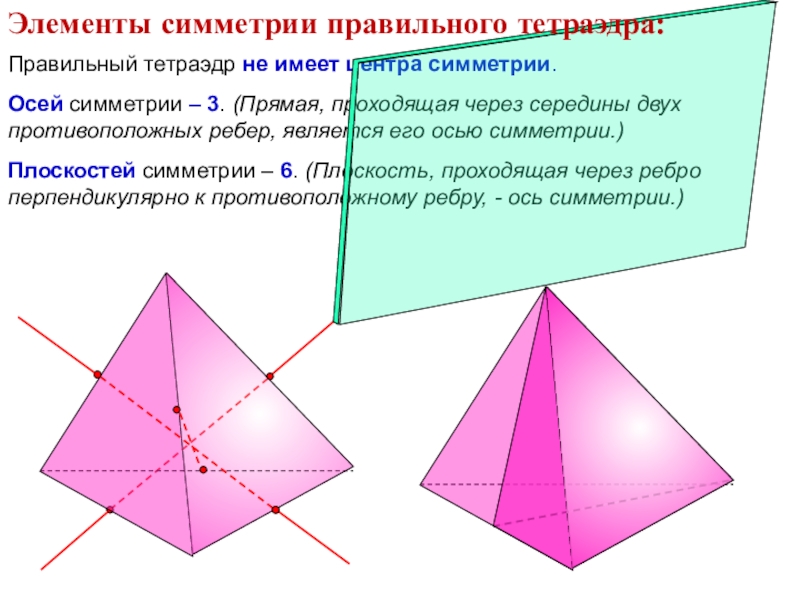
- 28. Правильный тетраэдр не имеет центра симметрии. Осей
- 29. ЗАДАНИЕ: Какой из представленных физических приборов обладает осевой симметрией?1243
- 30. ЗАДАНИЕ: Определите количество осей симметрии изображения.
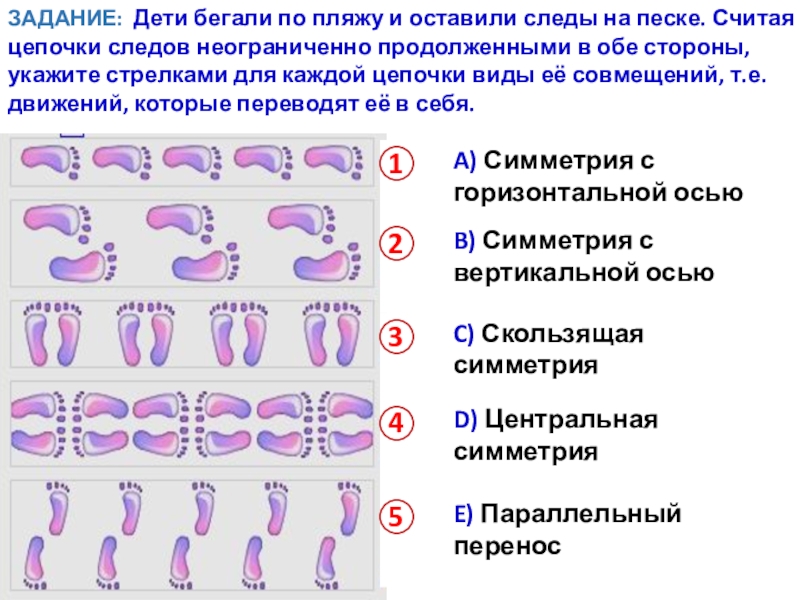
- 31. ЗАДАНИЕ: Дети бегали по пляжу и оставили
- 32. ПРОВЕРОЧНАЯ РАБОТАКритерии работы:Оценка «3» - выполнены
- 33. ОТВЕТЫ:
- 34. СПАСИБО ЗА УРОК!РЕФЛЕКСИЯ:
Симметрия в пространстве. Элементы симметрии правильных многогранников «Раз, стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия приятна для глаз? Что такое симметрия? Это врожденное чувство, отвечал
Слайд 1Урок математики в 10 классе:
«Симметрия в пространстве.
Элементы симметрии
правильных многогранников»
Слайд 2Симметрия в пространстве.
Элементы симметрии
правильных многогранников
«Раз, стоя перед черной
доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия приятна для глаз? Что такое симметрия? Это врожденное чувство, отвечал я сам себе. На чем же оно основано? Разве во всём в жизни есть симметрия?»
Л. Н. Толстой «Отрочество»
Л. Н. Толстой «Отрочество»
Слайд 3Толковый словарь русского языка В.И. Даля:
СИММЕТРИЯ - соразмер, соразмерность, равномерие, равнообразие,
соответствие, сходность; одинаковость, либо соразмерное подобие расположения частей целого, двух половин.
Новый словарь русского языка Т.Ф. Ефремовой:
СИММЕТРИЯ - соразмерное, пропорциональное расположение частей чего-либо по отношению к центру, середине.
Толковый словарь русского языка Д.Н.Ушакова:
СИММЕТРИЯ - пропорциональность, соразмерность в расположении частей целого в пространстве, полное соответствие (по расположению, величине) одной половины целого другой половине.
Слайд 4симметрия относительно точки
симметрия относительно прямой
симметрия относительно плоскости
СИММЕТРИЯ В
ПРОСТРАНСТВЕ (С. 75)
планиметрия
стереометрия
центральная
осевая
зеркальная
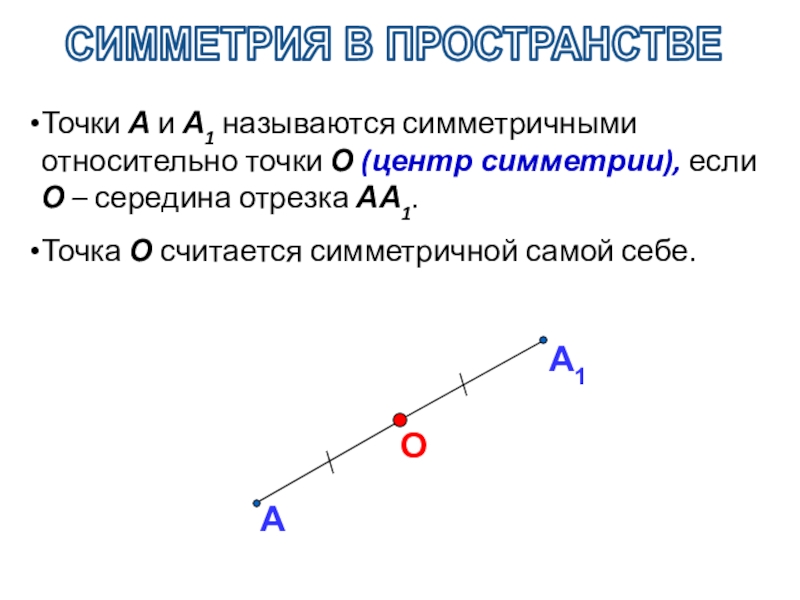
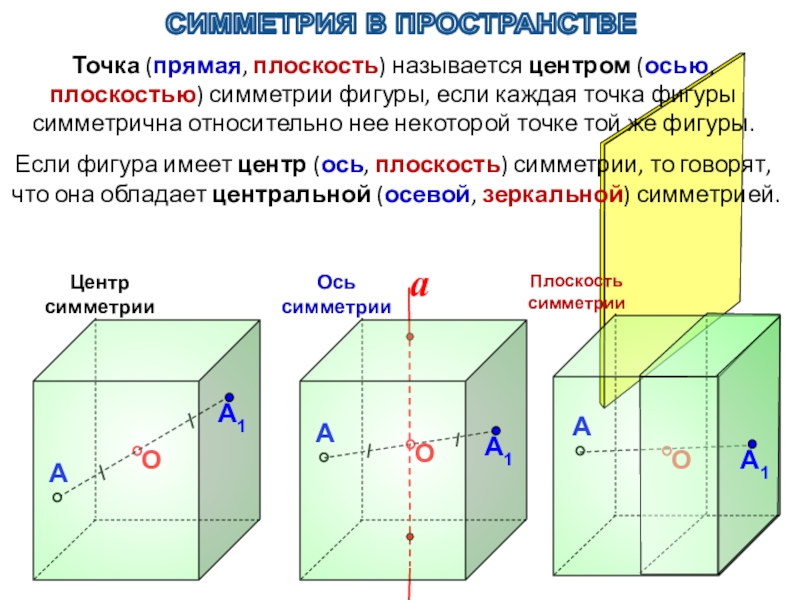
Слайд 5СИММЕТРИЯ В ПРОСТРАНСТВЕ
Точки А и А1 называются симметричными относительно точки О
(центр симметрии), если О – середина отрезка АА1.
Точка О считается симметричной самой себе.
Точка О считается симметричной самой себе.
А
О
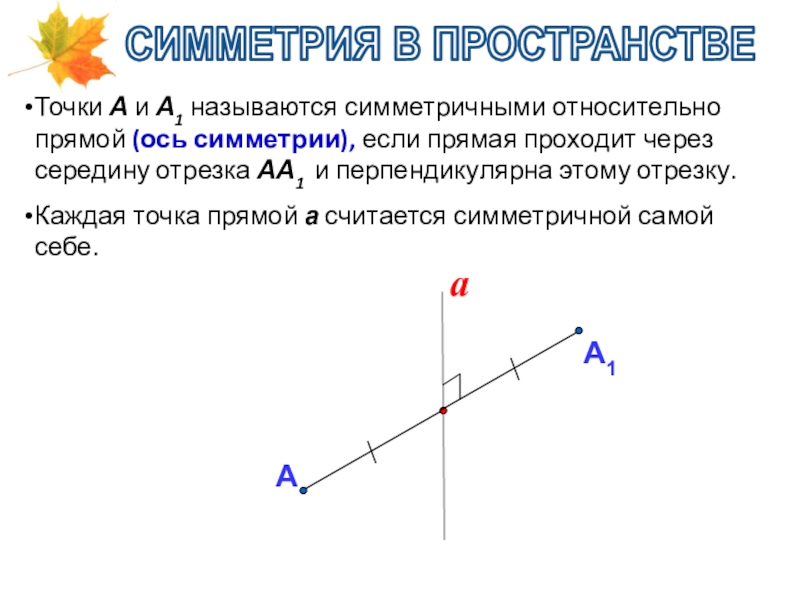
Слайд 6СИММЕТРИЯ В ПРОСТРАНСТВЕ
Точки А и А1 называются симметричными относительно прямой (ось
симметрии), если прямая проходит через середину отрезка АА1 и перпендикулярна этому отрезку.
Каждая точка прямой а считается симметричной самой себе.
Каждая точка прямой а считается симметричной самой себе.
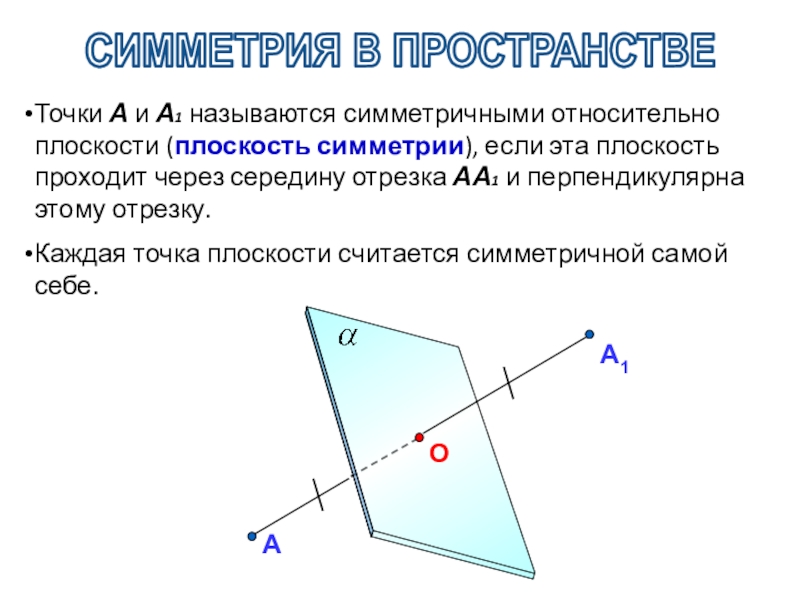
Слайд 7СИММЕТРИЯ В ПРОСТРАНСТВЕ
Точки А и А1 называются симметричными относительно плоскости (плоскость
симметрии), если эта плоскость проходит через середину отрезка АА1 и перпендикулярна этому отрезку.
Каждая точка плоскости считается симметричной самой себе.
Каждая точка плоскости считается симметричной самой себе.
А
Слайд 8Центр
симметрии
Плоскость симметрии
Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии фигуры,
если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры.
Если фигура имеет центр (ось, плоскость) симметрии, то говорят, что она обладает центральной (осевой, зеркальной) симметрией.
Если фигура имеет центр (ось, плоскость) симметрии, то говорят, что она обладает центральной (осевой, зеркальной) симметрией.
СИММЕТРИЯ В ПРОСТРАНСТВЕ
Слайд 9СИММЕТРИЯ В ФИЗИКЕ И ТЕХНИКЕ
Взаимосвязь электрического и
магнитного полей
Магнитные поля планет и Солнца
Слайд 12СИММЕТРИЯ В АРХИТЕКТУРЕ
Церковь Покрова Богородицы
Здание МГУ в Москве
Большой дворец в Стрельне
Константиновский
дворец
Слайд 16Эпиграф
«Правильных многогранников вызывающе мало, но этот весьма скромный по численности
отряд сумел пробраться в самые глубины различных наук»
Л. Кэрролл
Л. Кэрролл
Слайд 17Многогранник – поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело.
Слайд 18Выпуклый многогранник называется правильным, если все его грани – равные правильные
многоугольники и в каждой его вершине сходится равное число ребер.
Правильный многогранник
Слайд 19
Существует пять типов правильных выпуклых многогранников: правильный тетраэдр, куб, октаэдр,
додекаэдр, икосаэдр
Слайд 21Названия многогранников
Пришли из Древней Греции,
в них указывается число граней:
«тетра»
4;
«гекса» 6;
«окта» 8;
«додека» 12;
«икоса» 20;
«эдра» грань.
«гекса» 6;
«окта» 8;
«додека» 12;
«икоса» 20;
«эдра» грань.
Слайд 25 Правильные многогранники иногда называют Платоновыми телами, поскольку
они занимают видное место в философской картине мира, разработанной великим мыслителем Древней Греции Платоном.
Платон считал, что мир строится из четырёх «стихий» – огня , земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников.
Платон считал, что мир строится из четырёх «стихий» – огня , земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников.
Правильные многогранники
в философской картине мира Платона
Платон
(ок. 428 - ок. 348 до н.э.)
Слайд 26Куб (гексаэдр) – составлен из шести квадратов.
Каждая вершина куба является
вершиной трех квадратов.
Состав:
6 граней, 8 вершин и 12 ребер
Элементы симметрии куба:
один центр симметрии – точку пересечения его диагоналей;
осей симметрии – 9.
Слайд 28Правильный тетраэдр не имеет центра симметрии.
Осей симметрии – 3. (Прямая,
проходящая через середины двух противоположных ребер, является его осью симметрии.)
Плоскостей симметрии – 6. (Плоскость, проходящая через ребро перпендикулярно к противоположному ребру, - ось симметрии.)
Плоскостей симметрии – 6. (Плоскость, проходящая через ребро перпендикулярно к противоположному ребру, - ось симметрии.)
Элементы симметрии правильного тетраэдра:
Слайд 31ЗАДАНИЕ: Дети бегали по пляжу и оставили следы на песке. Считая
цепочки следов неограниченно продолженными в обе стороны, укажите стрелками для каждой цепочки виды её совмещений, т.е. движений, которые переводят её в себя.
Слайд 32ПРОВЕРОЧНАЯ РАБОТА
Критерии работы:
Оценка «3» - выполнены задания 1а, 2а, 3а;
Оценка «4» - выполнены задания 1б, 2б, 3б;
Оценка «5» - выполнены задания 1в, 2в, 3в.
