- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Параллельность плоскостей (10 класс)
Содержание
- 1. Презентация по геометрии Параллельность плоскостей (10 класс)
- 2. Геометрия – 10 Параллельность плоскостей
- 3. Задание на самоподготовку:П. 10-11 – разобрать и
- 4. Вопрос – ответ :
- 5. Вспомним:Определение параллельных прямых в пространстве.Теорема о параллельных
- 6. Вспомним:Аксиома 3. Если две плоскости имеют общую
- 7. Изучаем новое:Определение. Две плоскости называются параллельными, если они не пересекаются, то есть не имеют общих точек.
- 8. Изучаем новое:Теорема (Признак параллельности двух плоскостей). Если
- 9. Изучаем новое:Теорема (Признак параллельности двух плоскостей). Если
- 10. Изучаем новое:Задача. Докажите, что противолежащие грани параллелепипеда лежат в параллельных плоскостях.Доказательство. Что и требовалось доказать.
- 11. Изучаем новое:Доказательство. Что и требовалось доказать.
- 12. Если две параллельные плоскости пересечены третьей, то
- 13. Отрезки параллельных прямых, заключенные между параллельными плоскостями,
- 14. Упражнения: №№ 53,54
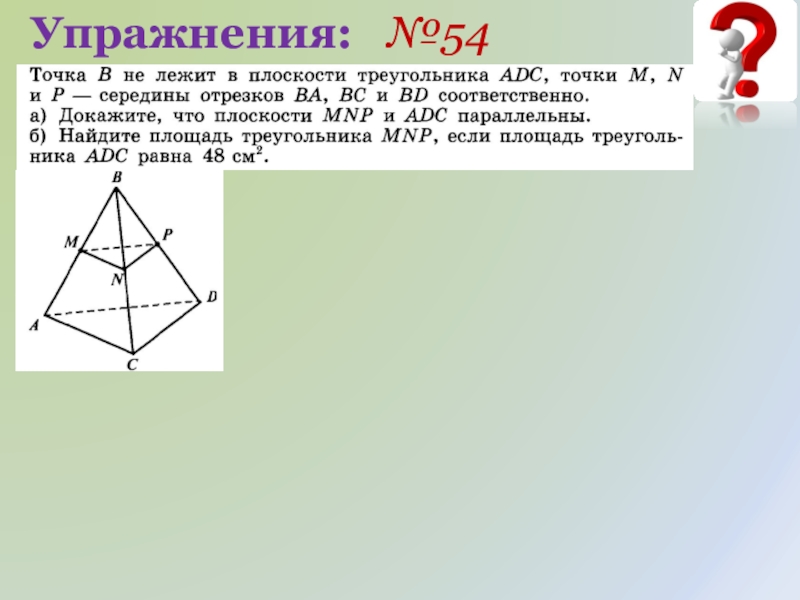
- 15. Упражнения: №54
- 16. Проверьте себя:Могут ли прямая и плоскость не
- 17. Подведем итог:Как бы вы закончили предложение?Сегодня на
Слайд 3Задание на самоподготовку:
П. 10-11 – разобрать и выучить.
Вопросы 1-13 на стр.
Выполнить упражнения:
№№ 55, 58, 59.
Слайд 5Вспомним:
Определение параллельных прямых в пространстве.
Теорема о параллельных прямых.
Лемма о пересечении плоскости
Теорема о параллельности трех прямых в пространстве.
Определение параллельных прямой и плоскости.
Признак параллельности прямой и плоскости.
Определение скрещивающихся прямых.
Признак скрещивающихся прямых.
Теорема о скрещивающихся прямых.
Теорема об углах с сонаправленными сторонами.
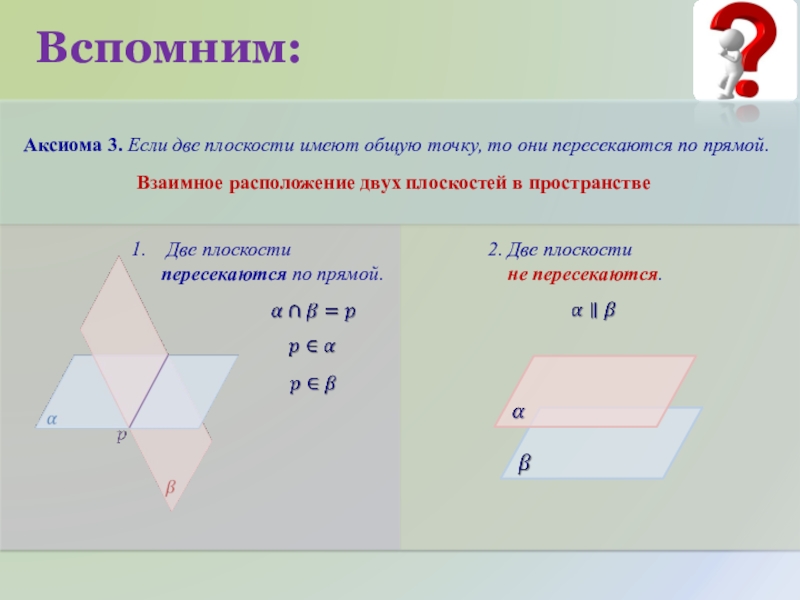
Слайд 6Вспомним:
Аксиома 3. Если две плоскости имеют общую точку, то они пересекаются
Взаимное расположение двух плоскостей в пространстве
Две плоскости
пересекаются по прямой.
2. Две плоскости
не пересекаются.
Слайд 7Изучаем новое:
Определение. Две плоскости называются параллельными, если они не пересекаются, то
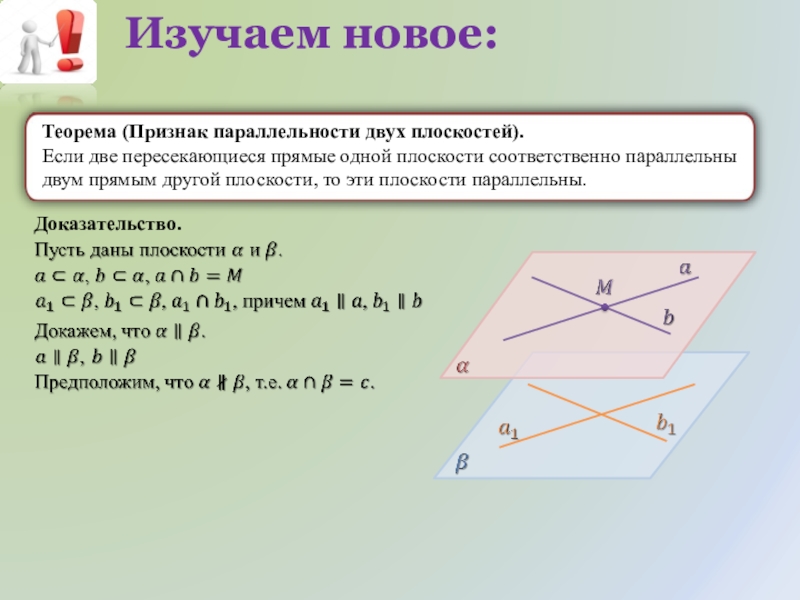
Слайд 8Изучаем новое:
Теорема (Признак параллельности двух плоскостей).
Если две пересекающиеся прямые одной
Доказательство.
Слайд 9Изучаем новое:
Теорема (Признак параллельности двух плоскостей).
Если две пересекающиеся прямые одной
Доказательство.
Теорема доказана.
Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Это не возможно.
Слайд 10Изучаем новое:
Задача. Докажите, что противолежащие грани параллелепипеда лежат в параллельных плоскостях.
Доказательство.
Что и требовалось доказать.
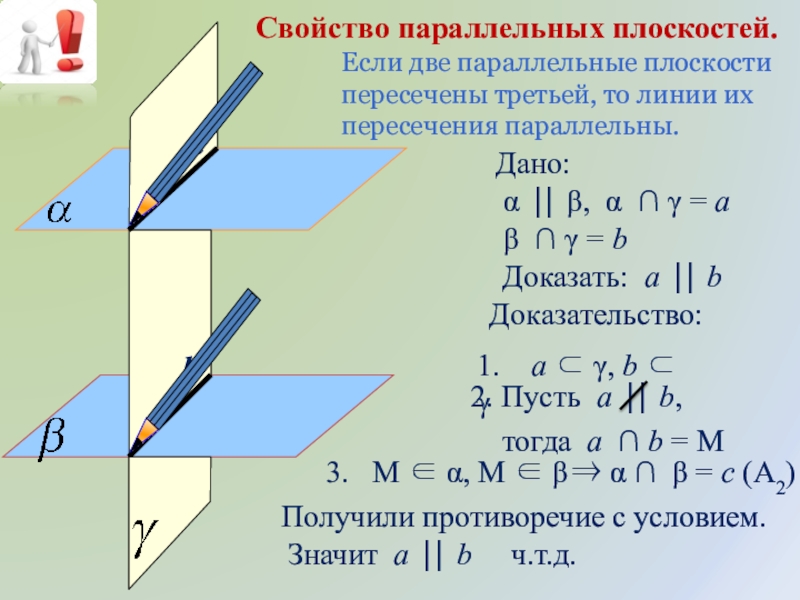
Слайд 12Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
Свойство параллельных плоскостей.
Дано:
α β, α = a
β = b
Доказать: a b
Доказательство:
1. a , b
2. Пусть a b,
тогда a b = М
3. M α, M β
α β = с (А2)
Получили противоречие с условием.
Значит a b ч.т.д.
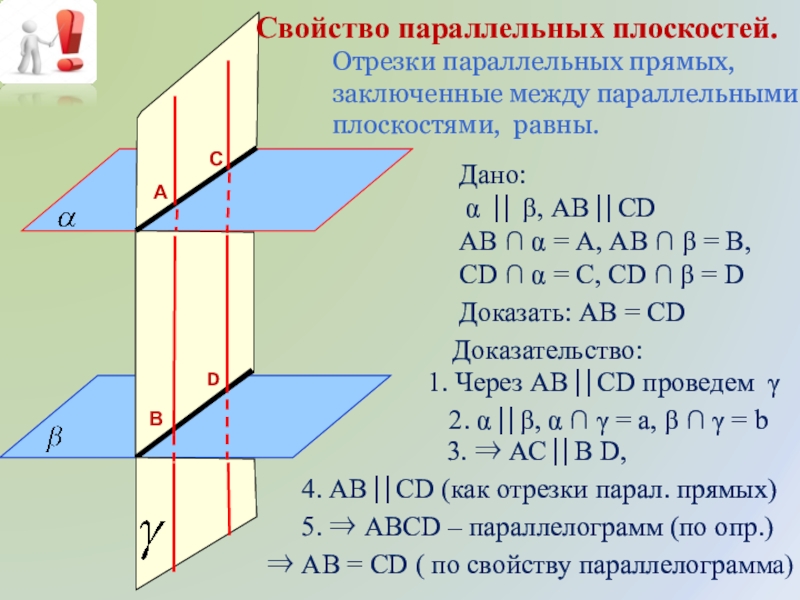
Слайд 13Отрезки параллельных прямых,
заключенные между параллельными плоскостями, равны.
Доказать: АВ = СD
Дано:
АВ α = А, АВ β = В,
СD α = С, СD β = D
Доказательство:
1. Через АВ СD проведем
2. α β, α = a, β = b
3. АС В D,
4. АВ СD (как отрезки парал. прямых)
5. АВСD – параллелограмм (по опр.)
АВ = СD ( по свойству параллелограмма)
Свойство параллельных плоскостей.
Слайд 16Проверьте себя:
Могут ли прямая и плоскость не иметь общих точек?
Верно ли,
Плоскости α и β параллельны, прямая т лежит в плоскости α. Верно ли, что прямая т параллельна плоскости β?
Верно ли, что если прямая а параллельна одной из двух параллельных плоскостей, то с другой плоскостью прямая а имеет одну общую точку?
Верно ли, что плоскости параллельны, если прямая, лежащая в одной плоскости, параллельна другой плоскости?
Да
Нет
Да
Нет
Нет
Слайд 17Подведем итог:
Как бы вы закончили предложение?
Сегодня на уроке я запомнила…….
Я научилась………………………………
Я
У меня не получилось………………….
Мне бы хотелось………………………..
Я справлюсь с домашней работой…