- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Основные понятия стереометрии. Аксиомы стереометрии 10 класс
Содержание
- 1. Презентация по геометрии Основные понятия стереометрии. Аксиомы стереометрии 10 класс
- 2. - Вспомните, что такое геометрия?Геометрия – это
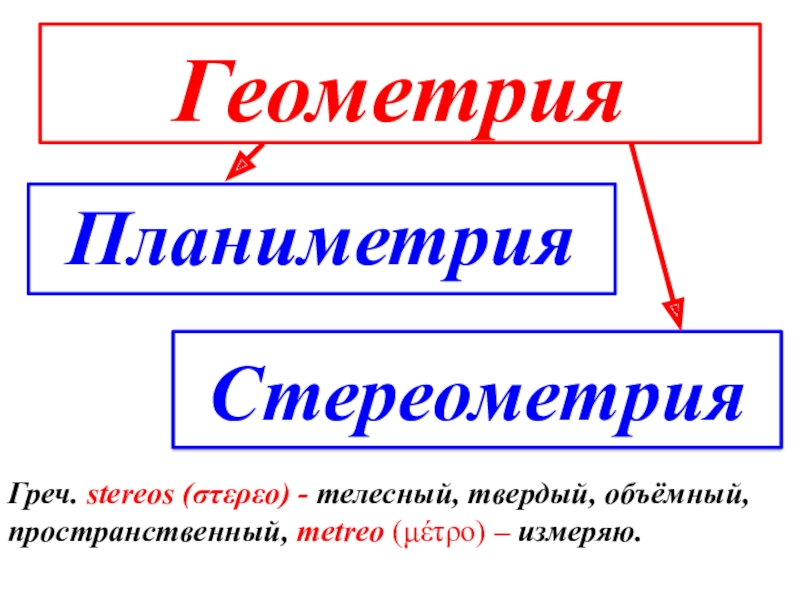
- 3. ГеометрияПланиметрияСтереометрия Греч. stereos (στερεο) - телесный, твердый, объёмный, пространственный, metreo (μέτρο) – измеряю.
- 4. Стереометрия- это раздел геометрии, в котором изучаются свойства фигур в пространстве.
- 5. Возникновение и развитие стереометрии.Развитие стереометрии началось позднее
- 6. Уже первобытный человек, перейдя от охоты к
- 7. Строитель даже самых древних примитивных построек должен
- 8. Строительство у древних египтян и жителей Месопотамии
- 9. Потребность земледелия, мореплавания, ориентировки во времени толкали
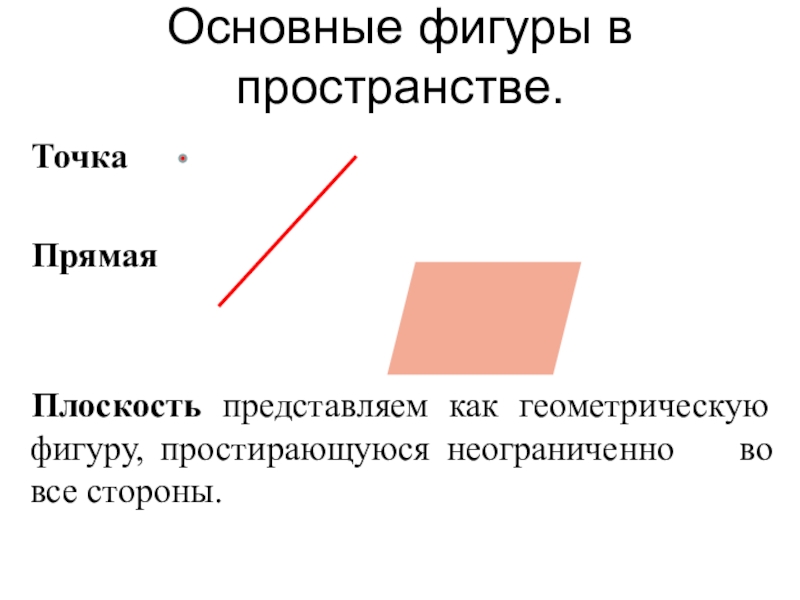
- 10. Основные фигуры в пространстве.Точка ПрямаяПлоскость представляем как геометрическую фигуру, простирающуюся неограниченно во все стороны.
- 11. Обозначение точек. Точки обозначаются прописными латинскими буквами А, В, С, …АВС
- 12. Примерами моделей точек являются:атомы и молекулы планеты в масштабах вселеннойкапли дождя
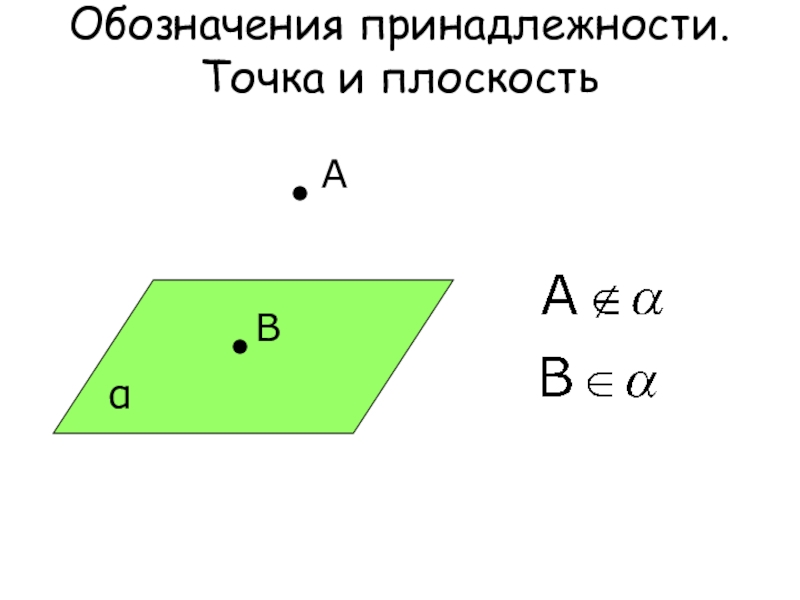
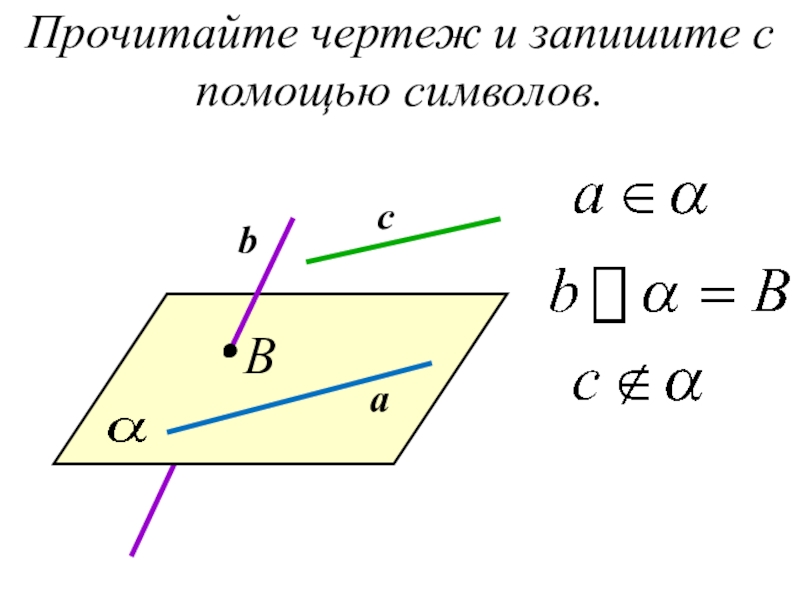
- 13. Обозначения принадлежности. Точка и плоскостьАВ
- 14. Обозначение прямых.Прямые обозначаются: строчными латинскими буквами a,
- 15. Примеры моделей прямых.инверсионные следы самолетоврельсы метеорные потоки
- 16. Обозначение плоскостей.Плоскости обозначаются греческими буквами α, β, γ,…или прописными латинскими: АВС или (АВС)…α(АВС)
- 17. Примеры моделей плоскостей.поверхность водыповерхность столаповерхность зеркала
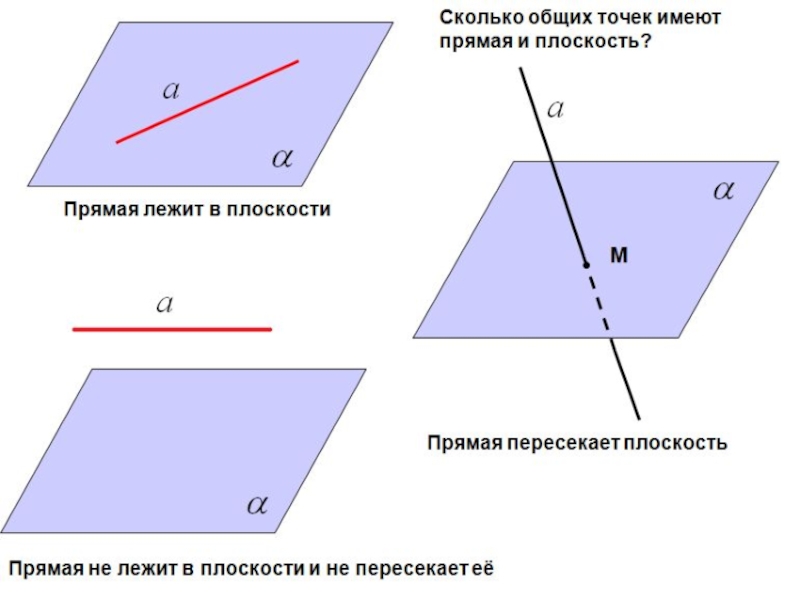
- 18. Обозначения. Прямая и плоскость.
- 19. Обозначения. Плоскости.
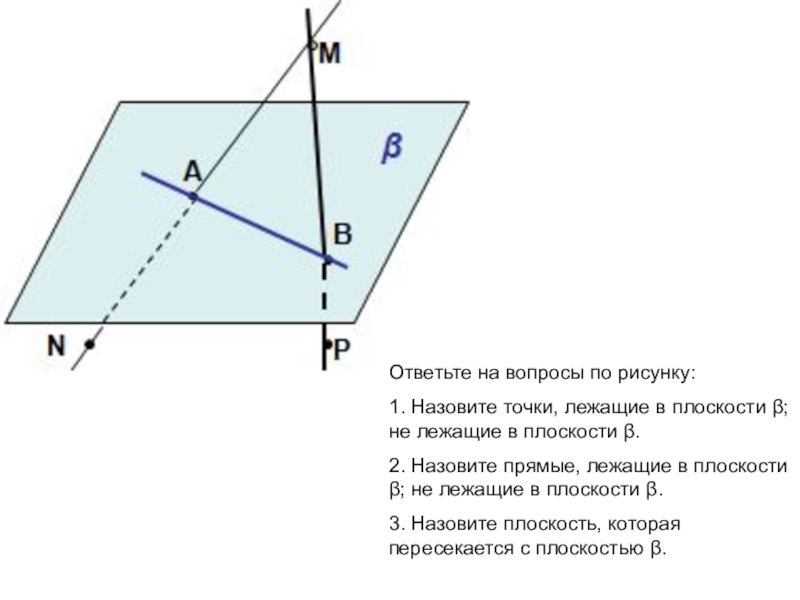
- 20. Ответьте на вопросы по рисунку:1. Назовите точки,
- 21. Что еще изучает стереометрия?Наряду с точкой, прямой и плоскостью стереометрия изучает геометрические тела и их свойства.
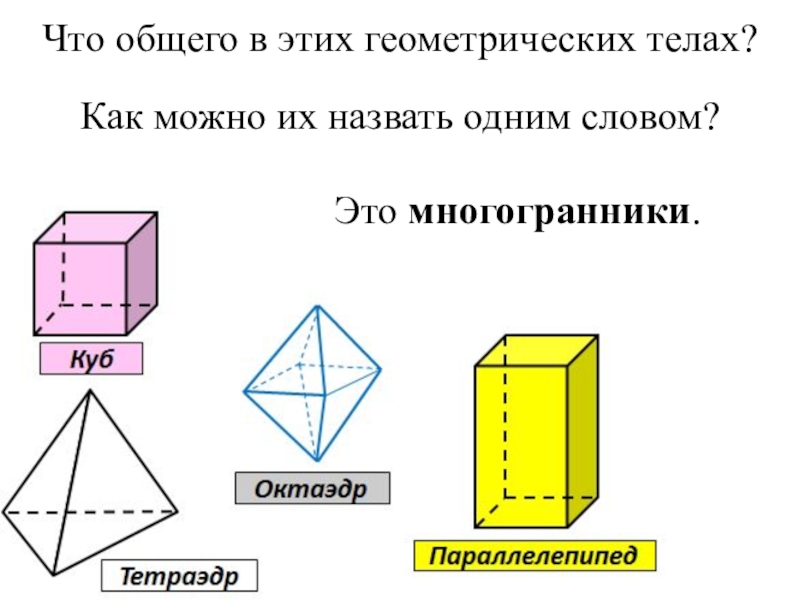
- 22. Что общего в этих геометрических телах?Как можно их назвать одним словом?Это многогранники.
- 23. Что общего в этих геометрических телах?Как можно
- 24. Окружающие нас предметы и геометрические тела.Окружающие нас
- 25. Назовите какие геометрические тела вам напоминают предметы,
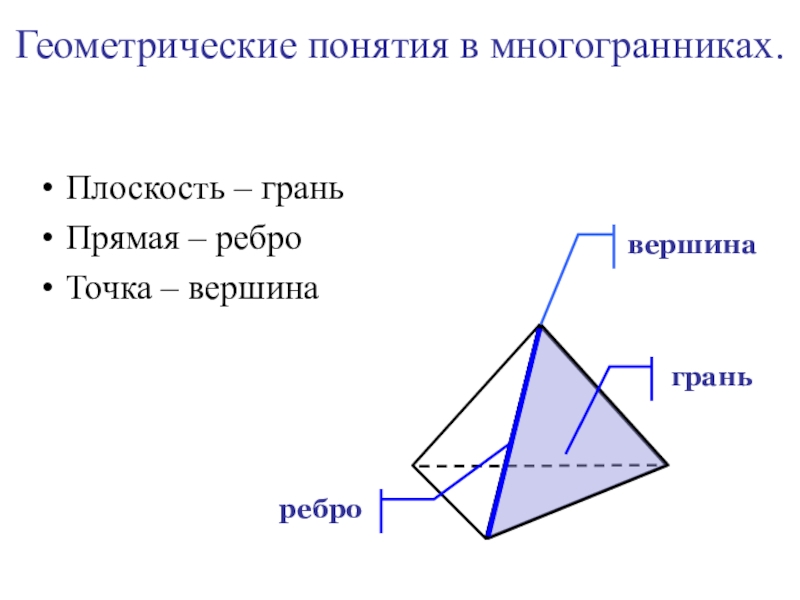
- 26. Геометрические понятия в многогранниках.Плоскость – граньПрямая – реброТочка – вершинавершинаграньребро
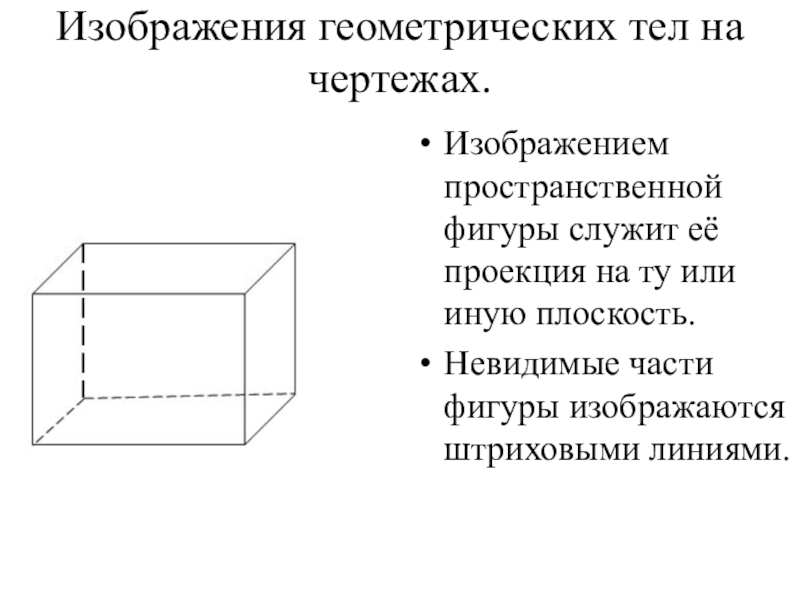
- 27. Изображения геометрических тел на чертежах.Изображением пространственной фигуры
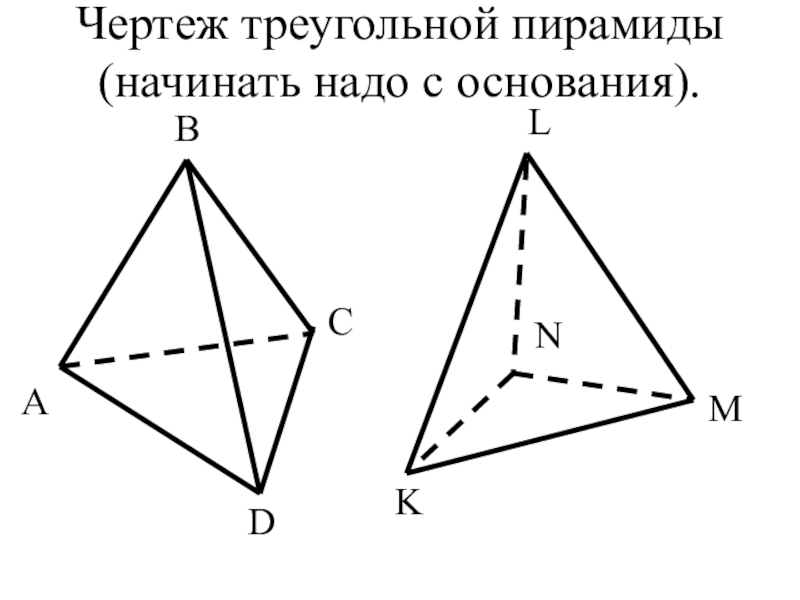
- 28. Чертеж треугольной пирамиды (начинать надо с основания).АDСВNMLK
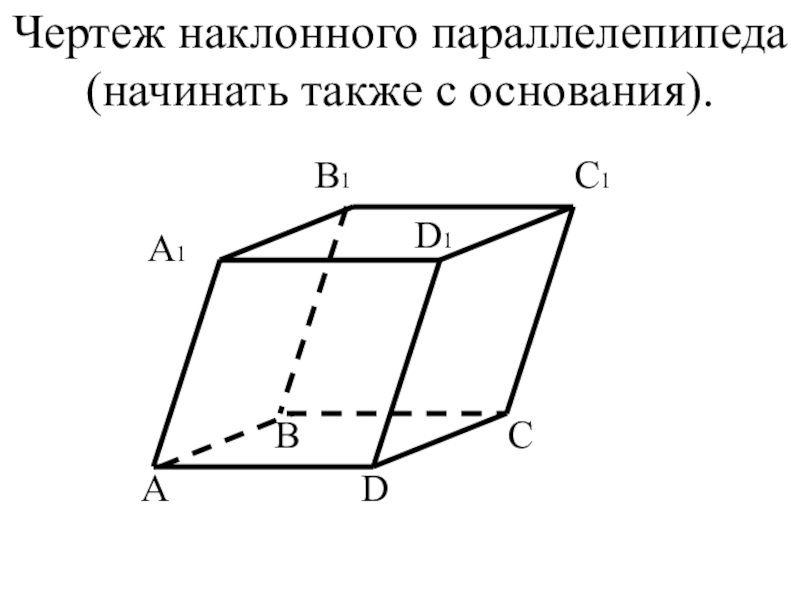
- 29. Чертеж наклонного параллелепипеда (начинать также с основания).АCBDА1D1C1B1
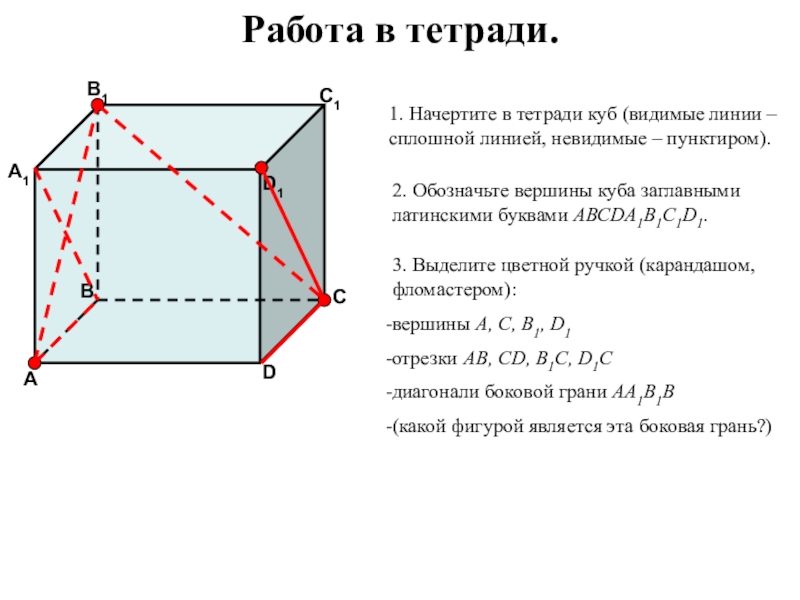
- 30. Работа в тетради.1. Начертите в тетради куб
- 31. Практическое (прикладное) значение стереометрии.Следует помнить, что геометрические
- 32. - Теперь давайте вспомним, что такое аксиома?Аксиома
- 33. 1. Аксиомы взаимного расположения точек и прямых.-
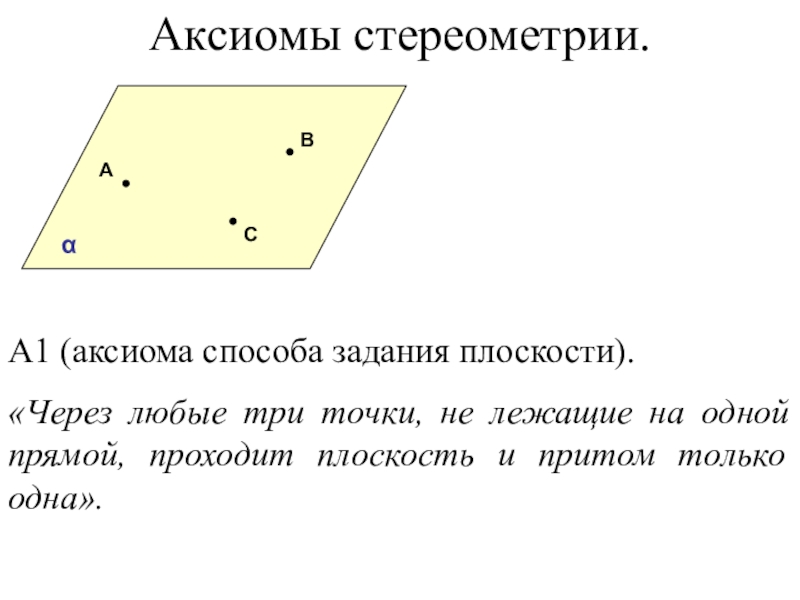
- 34. АВСА1 (аксиома способа задания плоскости). «Через
- 35. Эту аксиому можно продемонстрировать на простом примере.Если
- 36. Ответьте на вопрос. Верно ли, что:а) любые
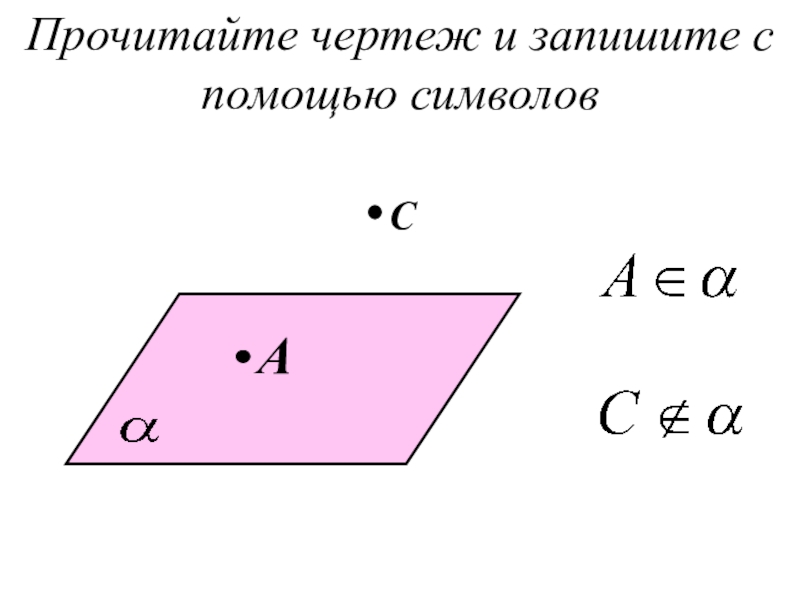
- 37. Прочитайте чертеж и запишите с помощью символовAС
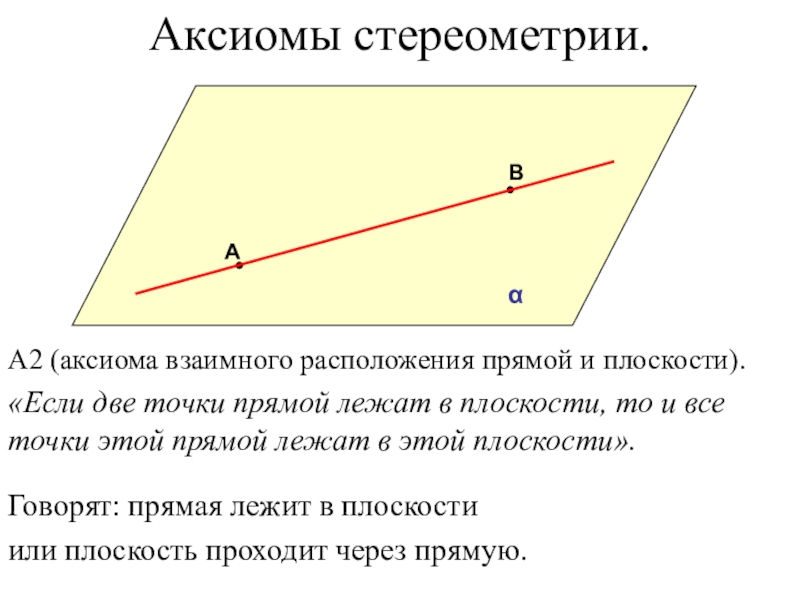
- 38. АВαА2 (аксиома взаимного расположения прямой и плоскости).
- 39. Слайд 39
- 40. Прочитайте чертеж и запишите с помощью символов.Bcba
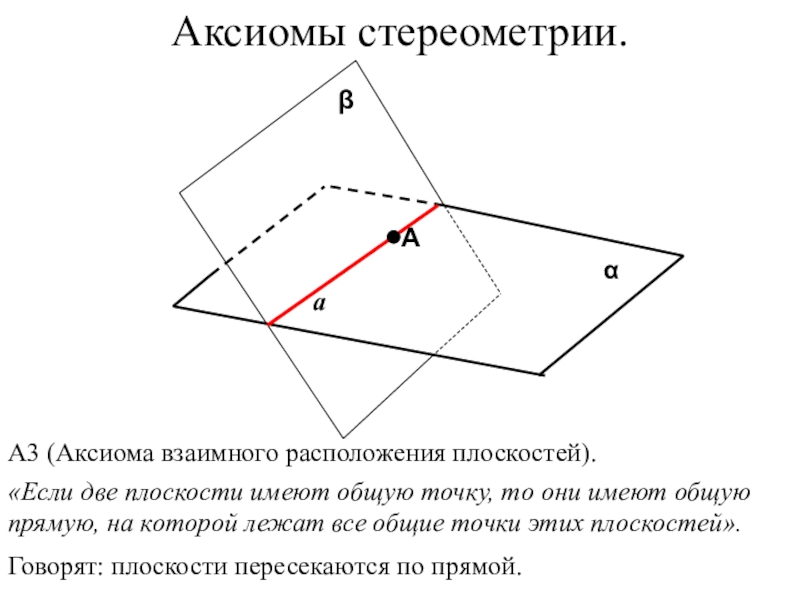
- 41. αβА3 (Аксиома взаимного расположения плоскостей). «Если
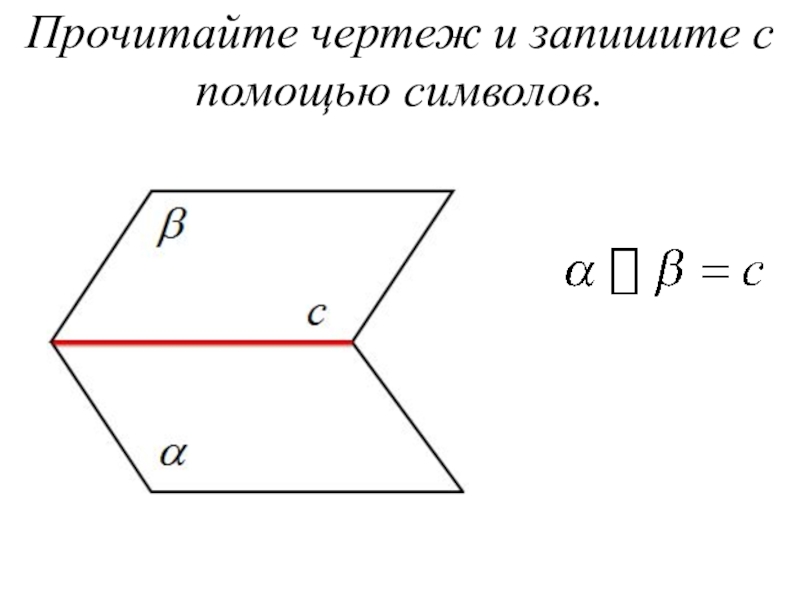
- 42. Прочитайте чертеж и запишите с помощью символов.
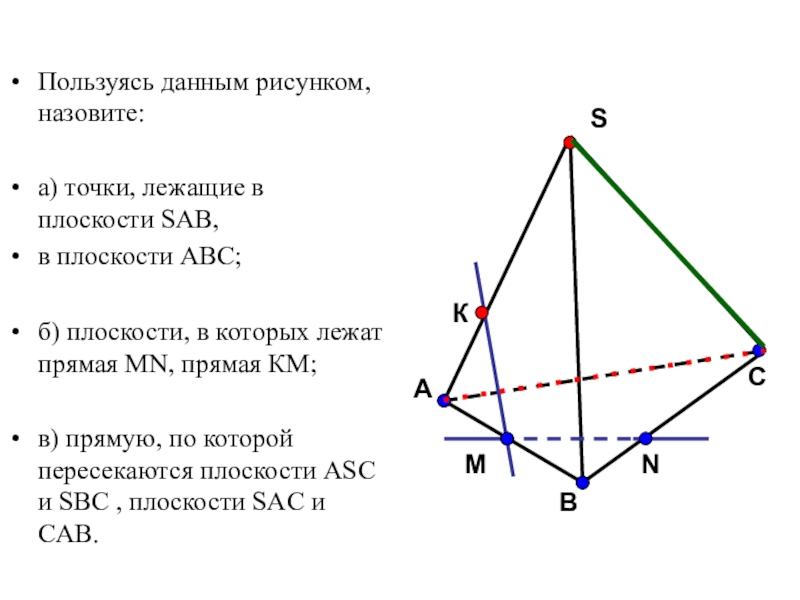
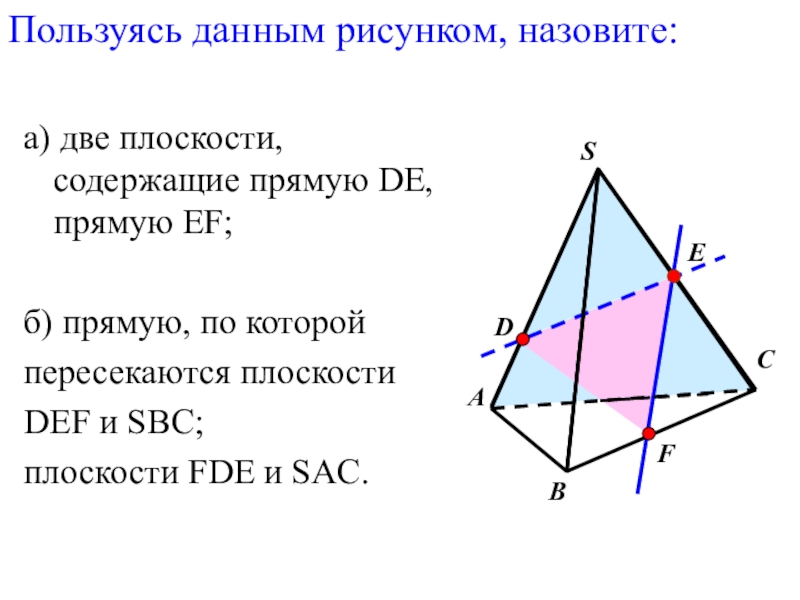
- 43. Пользуясь данным рисунком, назовите:а) точки, лежащие в
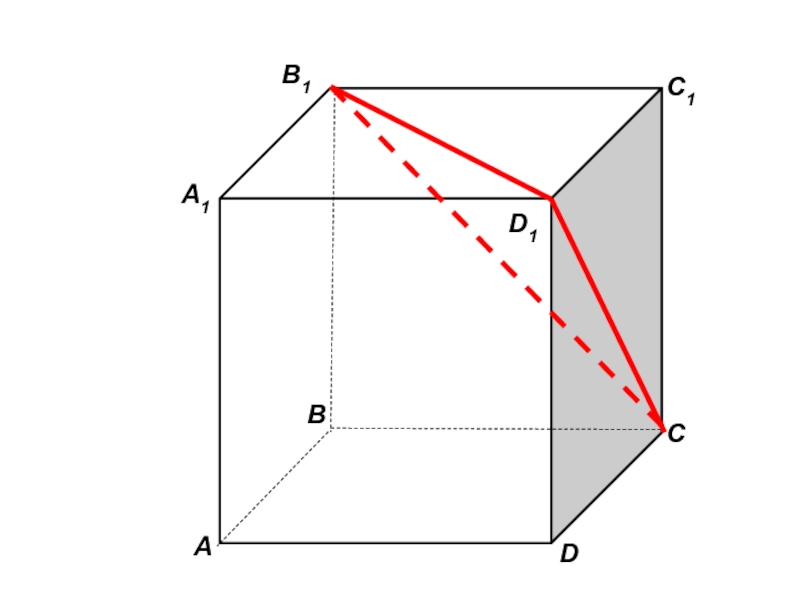
- 44. а) две плоскости, содержащие прямую DE, прямую
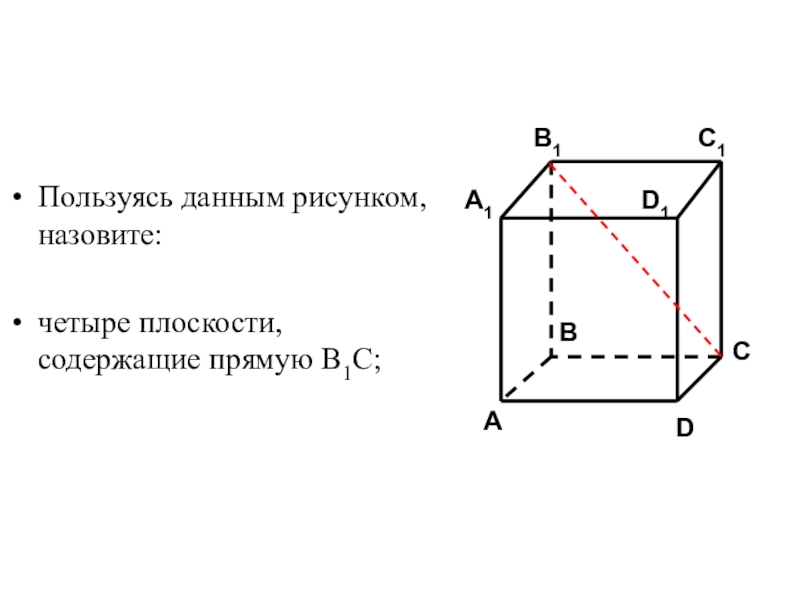
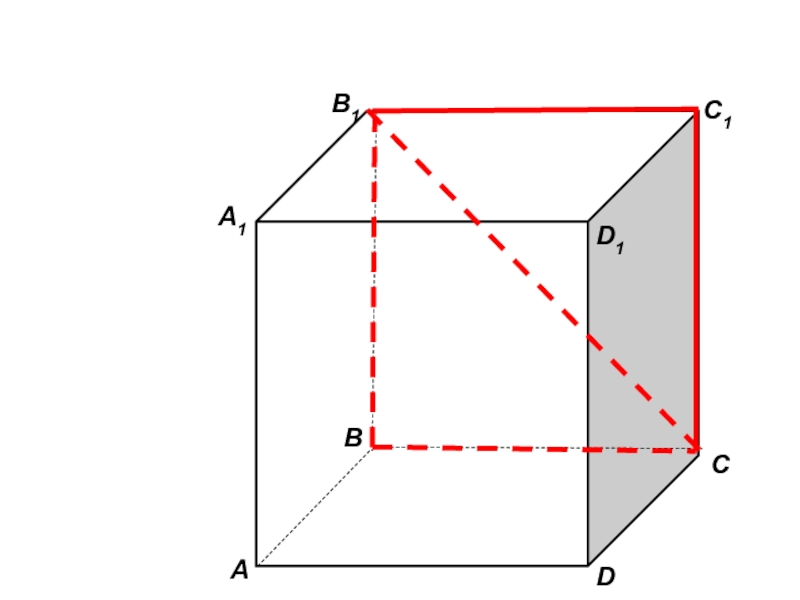
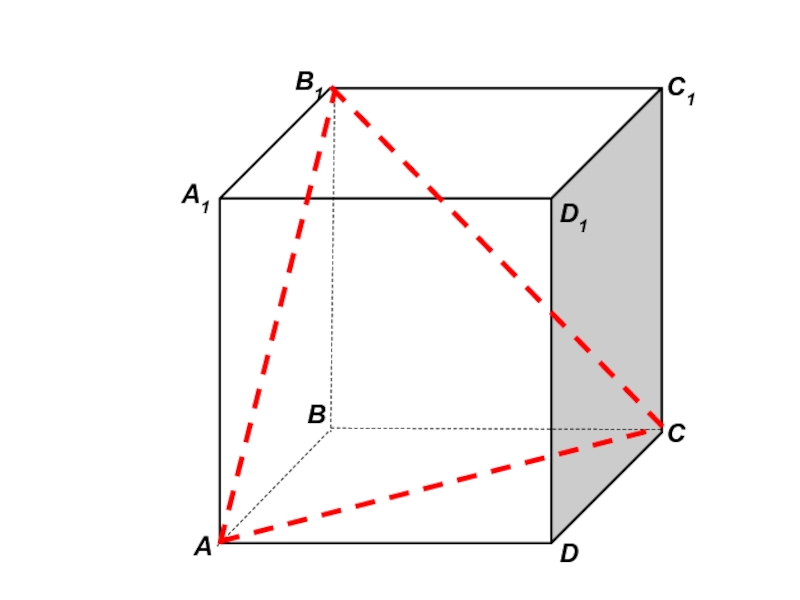
- 45. Пользуясь данным рисунком, назовите:четыре плоскости, содержащие прямую В1С;
- 46. АА1ВВ1СD1DC1
- 47. АА1ВВ1СD1DC1
- 48. АА1ВВ1СD1DC1
- 49. АА1ВВ1СD1DC1
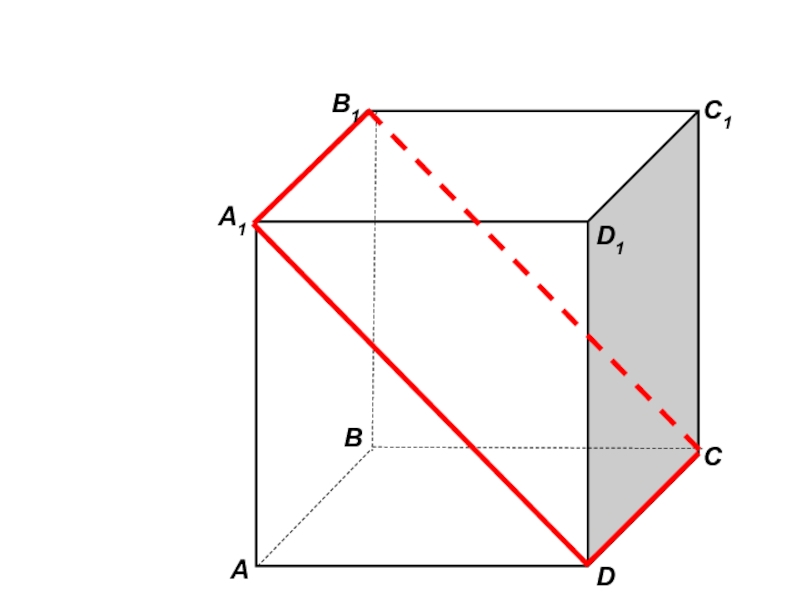
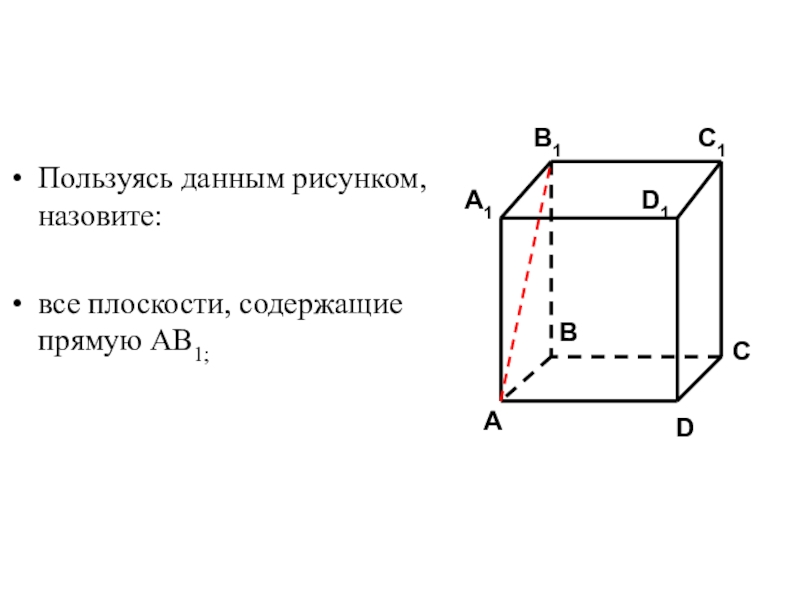
- 50. Пользуясь данным рисунком, назовите:все плоскости, содержащие прямую АВ1;
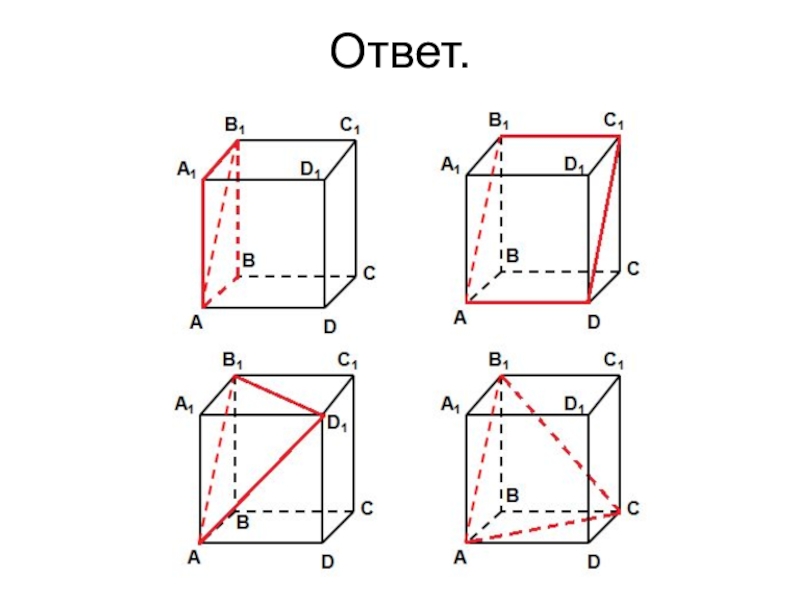
- 51. Ответ.
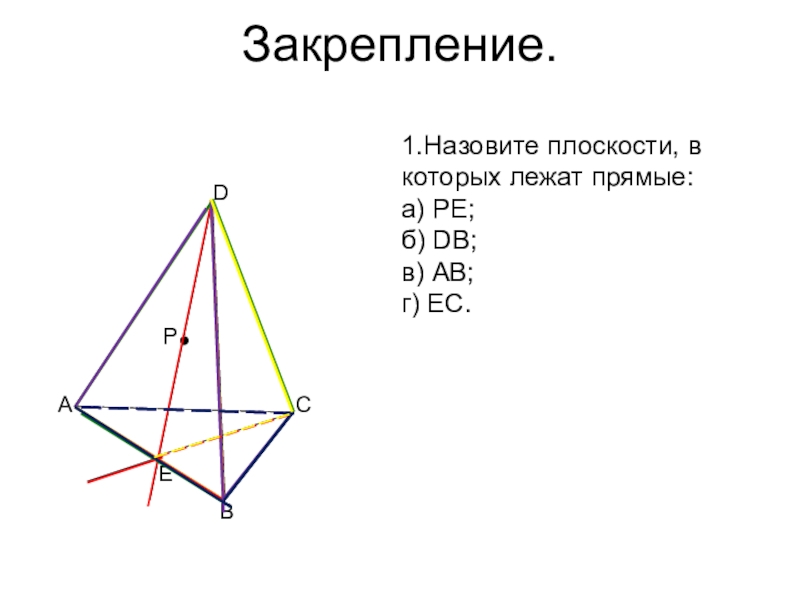
- 52. Закрепление.DCBAEP1.Назовите плоскости, в которых лежат прямые:а) PE; б) DB;в) AB; г) EC.
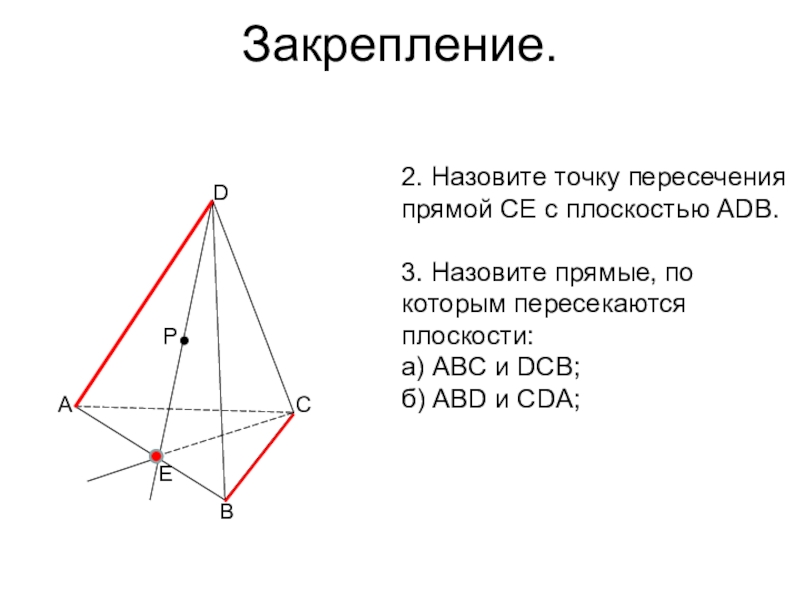
- 53. Закрепление.DCBAEP2. Назовите точку пересечения прямой СE с
- 54. Итог урока.1) Как называется раздел геометрии, который
- 55. Домашнее задание:Повторить аксиомы планиметрии, выучить аксиомы стереометрии.Прочитать
Слайд 2- Вспомните, что такое геометрия?
Геометрия – это наука о свойствах геометрических
Геометрия – от двух греч. слов: geo(η γη) – земля, metreo (μέτρο) – измеряю.
- Что такое планиметрия?
Планиметрия – раздел геометрии, в котором изучаются свойства фигур на плоскости.
А
а
Основные понятия планиметрии:
точка
прямая
- Какие основные понятия в планиметрии вы знаете?
Планиметрия – от двух слов: лат. planum - плоскость и греч. metreo (μέτρο) - измеряю.
Слайд 3Геометрия
Планиметрия
Стереометрия
Греч. stereos (στερεο) - телесный, твердый, объёмный, пространственный, metreo (μέτρο)
Слайд 5Возникновение и развитие стереометрии.
Развитие стереометрии началось позднее планиметрии, но также в
Стереометрия развивалась из наблюдений и решений вопросов, которые возникали в процессе практической деятельности человека: построение зданий и средств передвижения, рытьё каналов; изучение небесной сферы, сбор урожая…
Слайд 6
Уже первобытный человек, перейдя от охоты к земледелию, делал попытки оценивать,
Слайд 7
Строитель даже самых древних примитивных построек должен был как-то учитывать материал,
Слайд 8
Строительство у древних египтян и жителей Месопотамии требовало знакомства с
Слайд 9Потребность земледелия, мореплавания, ориентировки во времени толкали людей к астрономическим наблюдениям,
Слайд 10Основные фигуры в пространстве.
Точка
Прямая
Плоскость представляем как геометрическую фигуру, простирающуюся неограниченно
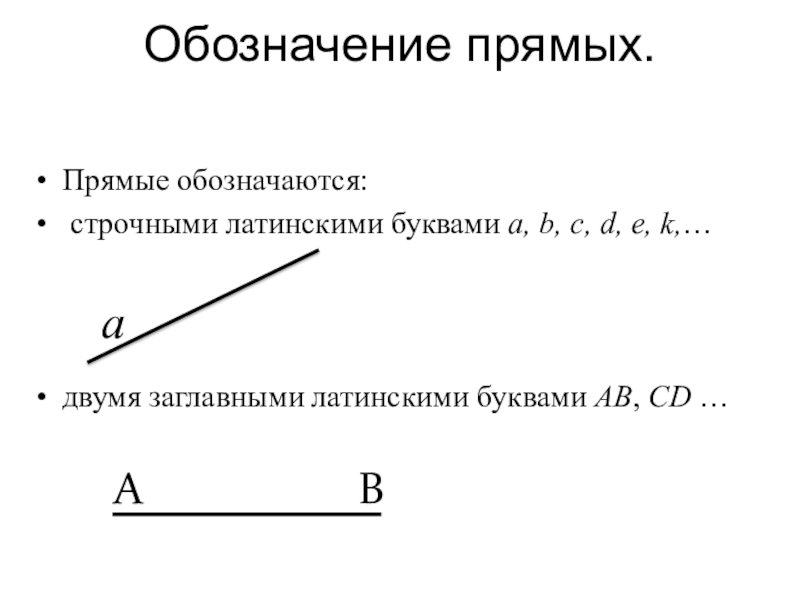
Слайд 14Обозначение прямых.
Прямые обозначаются:
строчными латинскими буквами a, b, c, d, e,
двумя заглавными латинскими буквами AB, CD …
а
A
B
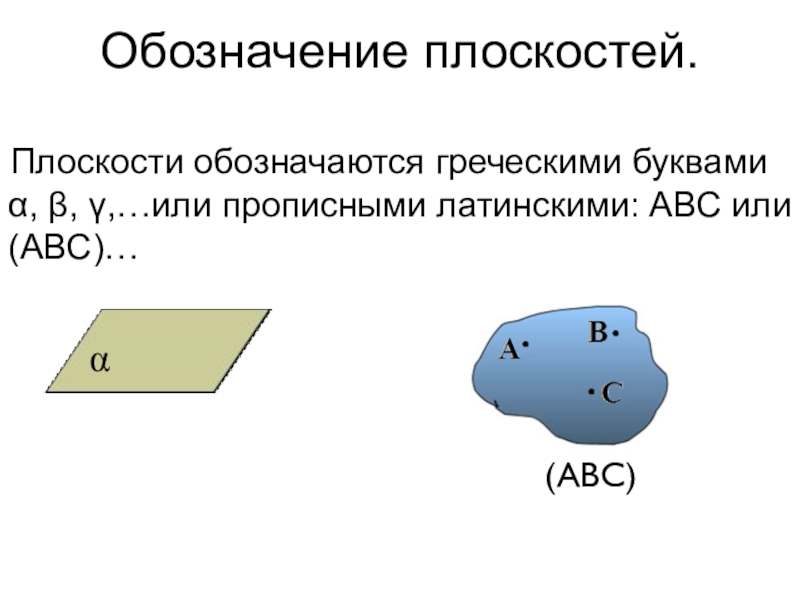
Слайд 16Обозначение плоскостей.
Плоскости обозначаются греческими буквами α, β, γ,…или прописными латинскими: АВС
α
(АВС)
Слайд 20Ответьте на вопросы по рисунку:
1. Назовите точки, лежащие в плоскости β;
2. Назовите прямые, лежащие в плоскости β; не лежащие в плоскости β.
3. Назовите плоскость, которая пересекается с плоскостью β.
Слайд 21Что еще изучает стереометрия?
Наряду с точкой, прямой и плоскостью стереометрия изучает
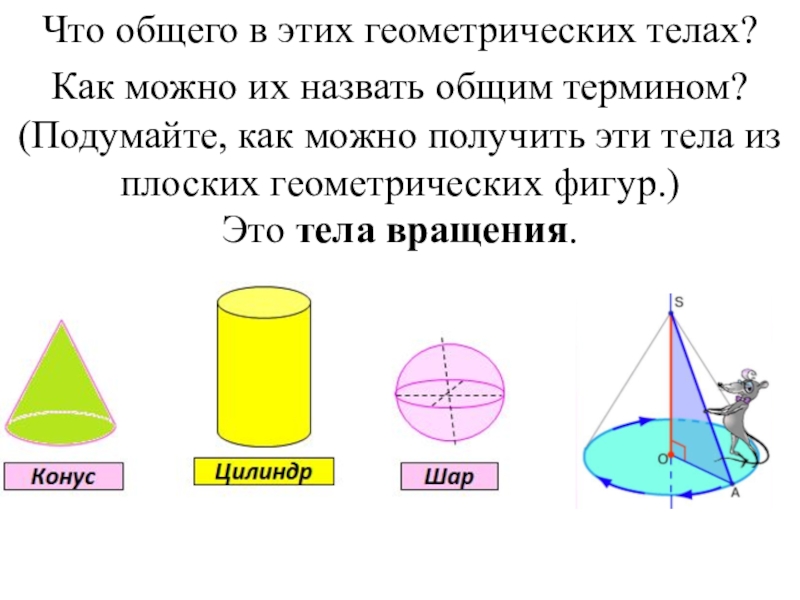
Слайд 23Что общего в этих геометрических телах?
Как можно их назвать общим термином?
Это тела вращения.
Слайд 24Окружающие нас предметы и геометрические тела.
Окружающие нас предметы дают представления о
А изучая свойства геометрических фигур – воображаемых объектов, мы получаем сведения о геометрических свойствах реальных предметов и можем использовать эти свойства в практической деятельности.
Слайд 25Назовите какие геометрические тела вам напоминают предметы, изображенные на этих рисунках:
Назовите
Слайд 26Геометрические понятия в многогранниках.
Плоскость – грань
Прямая – ребро
Точка – вершина
вершина
грань
ребро
Слайд 27Изображения геометрических тел на чертежах.
Изображением пространственной фигуры служит её проекция на
Невидимые части фигуры изображаются штриховыми линиями.
Слайд 30Работа в тетради.
1. Начертите в тетради куб (видимые линии – сплошной
2. Обозначьте вершины куба заглавными латинскими буквами АВСDА1В1С1D1.
А
В
С
D
D1
С1
В1
А1
3. Выделите цветной ручкой (карандашом, фломастером):
вершины А, С, В1, D1
отрезки АВ, СD, В1С, D1С
диагонали боковой грани АА1В1В
(какой фигурой является эта боковая грань?)
Слайд 31Практическое (прикладное) значение стереометрии.
Следует помнить, что геометрические тела являются вымышленными объектами.
Изучая
Стереометрия широко используется в строительном деле, архитектуре, машиностроении и других областях науки и техники.
Стереометрические знания широко используются в быту: рассчитать объём, вычислить оптимальную высоту для крыши на даче и т.д.
Слайд 32- Теперь давайте вспомним, что такое аксиома?
Аксиома (от греч. axíõma (αξίωμα)
- Вот что говорил об аксиомах немецкий философ Фридрих Энгельс:
"Так называемые аксиомы математики – это те немногие мыслительные определения, которые необходимы в математике в качестве исходного пункта».
А Евклиду приписывают слова:
«Если теорему так и не смогли доказать, то она становится аксиомой».
Слайд 331. Аксиомы взаимного расположения точек и прямых.
- Каждой прямой принадлежат по
- Имеются по крайней мере три точки, не лежащие на одной прямой.
- Через любые две точки проходит прямая и притом только одна.
- Из трех точек прямой одна, и только одна, лежит между двумя другими.
2. Аксиома параллельности.
- Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
3. Существуют и другие аксиомы: аксиомы измерения и откладывания отрезков и углов, аксиомы равенства фигур и т.д.
- Аксиомы стереометрии состоят из всех аксиом планиметрии и трёх аксиом стереометрии.
- Давайте вспомним аксиомы планиметрии.
- Перейдём теперь к аксиомам стереометрии.
Слайд 34А
В
С
А1 (аксиома способа задания плоскости).
«Через любые три точки, не
α
Аксиомы стереометрии.
Слайд 35Эту аксиому можно продемонстрировать на простом примере.
Если ножки стола не одинаковы
Именно поэтому некоторые декоративные столики делают с тремя ножками. Этого достаточно для устойчивости.
Слайд 36Ответьте на вопрос. Верно ли, что:
а) любые три точки лежат в
б) любые четыре точки лежат в одной плоскости;
в) любые четыре точки не лежат в одной плоскости;
г) через любые три точки проходит плоскость, и притом только одна?
д) любые три точки не лежат в одной плоскости.
Слайд 38А
В
α
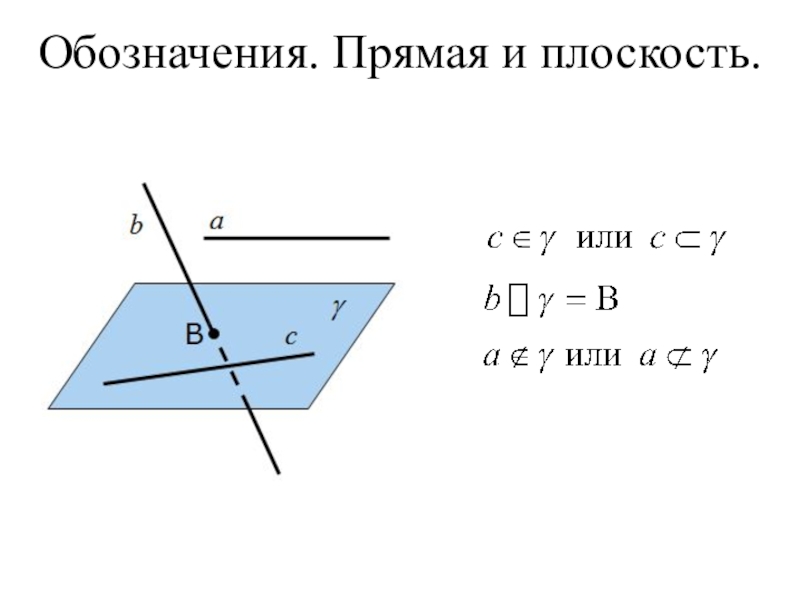
А2 (аксиома взаимного расположения прямой и плоскости).
«Если две точки
Говорят: прямая лежит в плоскости
или плоскость проходит через прямую.
Аксиомы стереометрии.
Слайд 41α
β
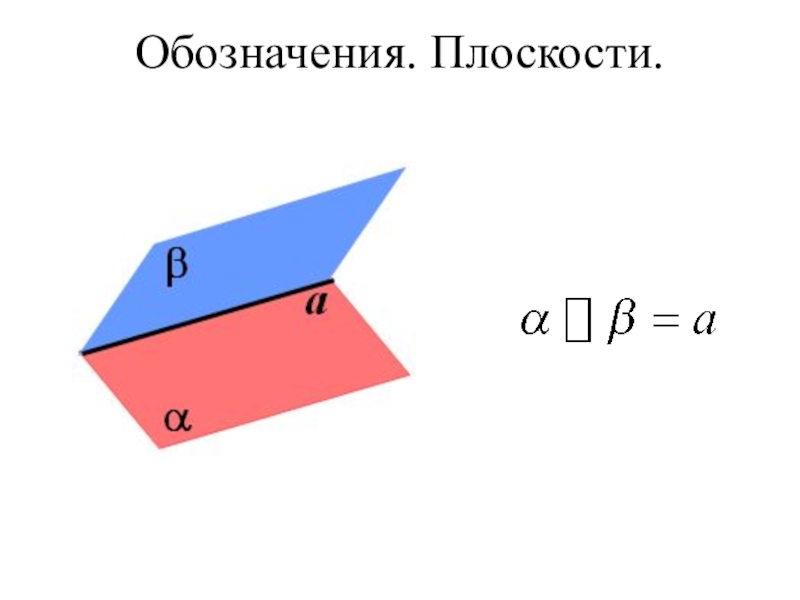
А3 (Аксиома взаимного расположения плоскостей).
«Если две плоскости имеют общую
А
а
Аксиомы стереометрии.
Говорят: плоскости пересекаются по прямой.
Слайд 43Пользуясь данным рисунком, назовите:
а) точки, лежащие в плоскости SAB,
в плоскости
б) плоскости, в которых лежат прямая MN, прямая КМ;
в) прямую, по которой пересекаются плоскости ASC и SBC , плоскости SAC и CAB.
Слайд 44а) две плоскости, содержащие прямую DE, прямую EF;
б) прямую, по которой
пересекаются
DEF и SBC;
плоскости FDE и SAC.
Пользуясь данным рисунком, назовите:
Слайд 53Закрепление.
D
C
B
A
E
P
2. Назовите точку пересечения прямой СE с плоскостью ADB.
3. Назовите прямые,
а) ABC и DCB;
б) ABD и CDA;
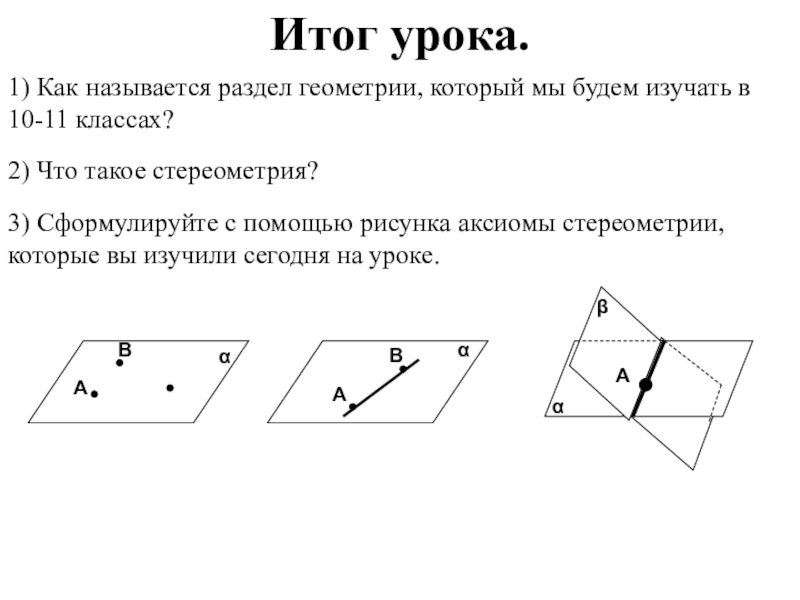
Слайд 54Итог урока.
1) Как называется раздел геометрии, который мы будем изучать в
2) Что такое стереометрия?
3) Сформулируйте с помощью рисунка аксиомы стереометрии, которые вы изучили сегодня на уроке.
А
А
В
В
α
α
А
α
β
Слайд 55Домашнее задание:
Повторить аксиомы планиметрии, выучить аксиомы стереометрии.
Прочитать пункты: Введение, 1, 2
Решить задачи: № 1; 2 (обязательно),
№ 3; 4 ( по желанию)