- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Окружность и круг (8,9 классы)
Содержание
- 1. Презентация по геометрии Окружность и круг (8,9 классы)
- 2. ПланI. Основные положения теории.II. Задачи по готовым
- 3. Основные положения теории 1.Окружность2. Вписанные углы3. Многоугольники4. Длина окружности и площадь круга
- 4. Дайте названия линиям и точкам Какой формулой
- 5. ОкружностьДва радиуса одной окружности равны.
- 6. ∆ОМК – равнобедренный и обладает всеми свойствами
- 7. Касательная к окружности перпендикулярна радиусу, проведенному в
- 8. Отрезки касательных равны∆AOB и ∆AOD – прямоугольные
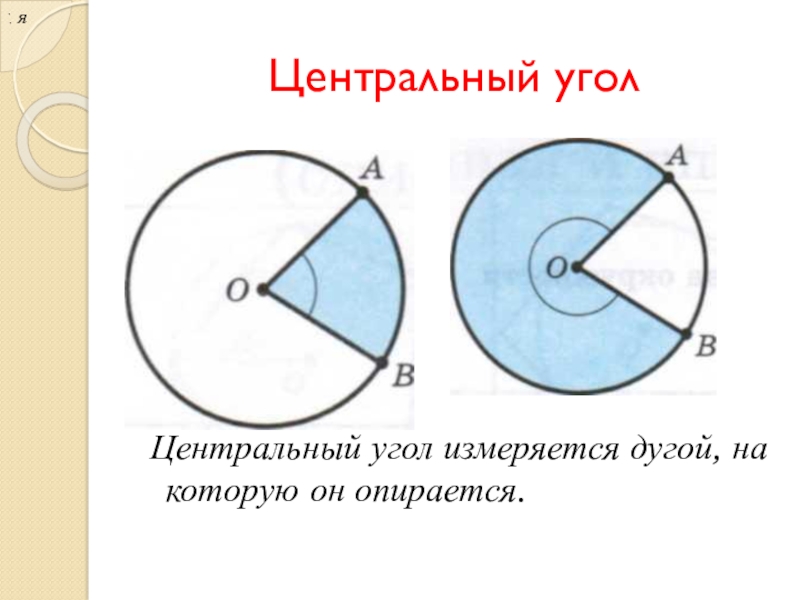
- 9. Центральный угол Центральный угол измеряется дугой, на которую он опирается... я
- 10. Вписанные углыУгол, вписанный в окружность, равен половине
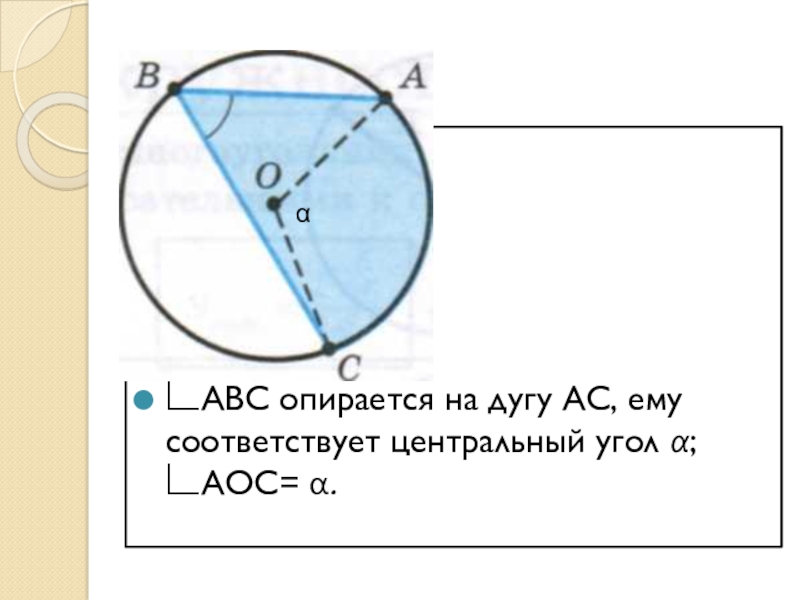
- 11. ∟ABC опирается на дугу AC, ему соответствует центральный угол α; ∟AOC= α.α
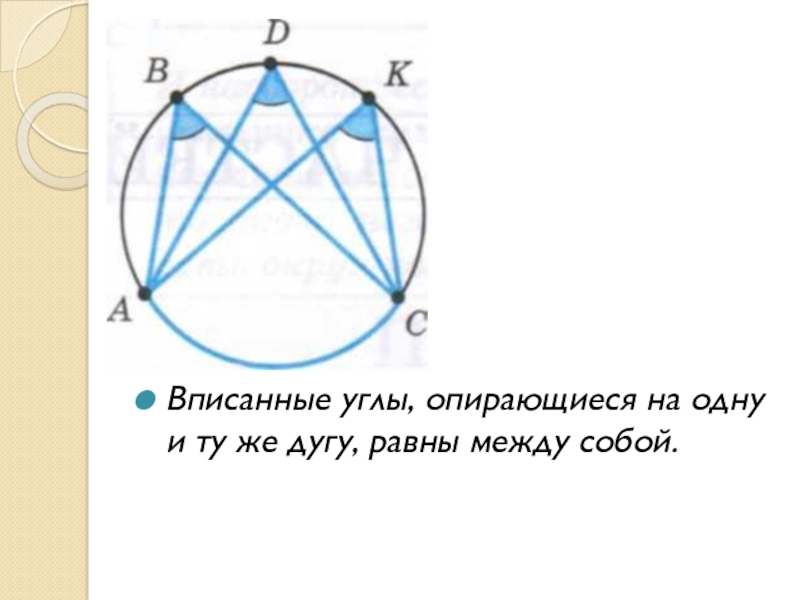
- 12. Вписанные углы, опирающиеся на одну и ту же дугу, равны между собой.
- 13. Многоугольник1. В выпуклом многоугольнике: сумма углов
- 14. Правильный многоугольникПравильный треугольникКвадратПравильный пятиугольникПравильный шестиугольник
- 15. ОRrВ правильном многоугольнике:1) все стороны и все
- 16. При решении задач часто бывает полезно находить
- 17. Длина окружности и площадь кругаОrДлина окружности:
ПланI. Основные положения теории.II. Задачи по готовым чертежам.III. Тестовые задания в соответствии заданиями КИМов.IV. Дополнительные вопросы теории и текстовые задачи к части 2.
Слайд 2План
I. Основные положения теории.
II. Задачи по готовым чертежам.
III. Тестовые задания в
соответствии заданиями КИМов.
IV. Дополнительные вопросы теории и текстовые задачи к части 2.
IV. Дополнительные вопросы теории и текстовые задачи к части 2.
Слайд 3
Основные положения теории
1.Окружность
2. Вписанные углы
3. Многоугольники
4. Длина окружности и площадь круга
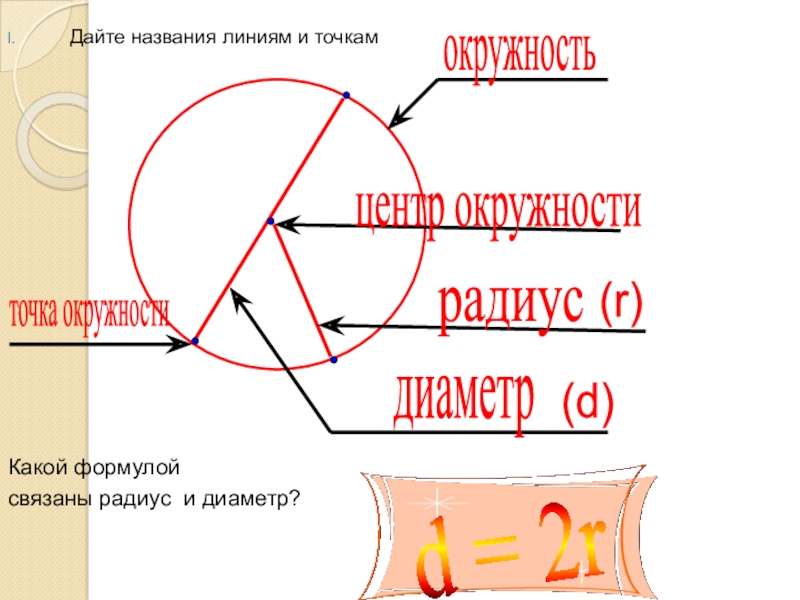
Слайд 4Дайте названия линиям и точкам
Какой формулой
связаны радиус и диаметр?
???
окружность
???
центр окружности
???
радиус
???
диаметр
(r)
(d)
???
d = 2r
???
точка окружности
Слайд 5
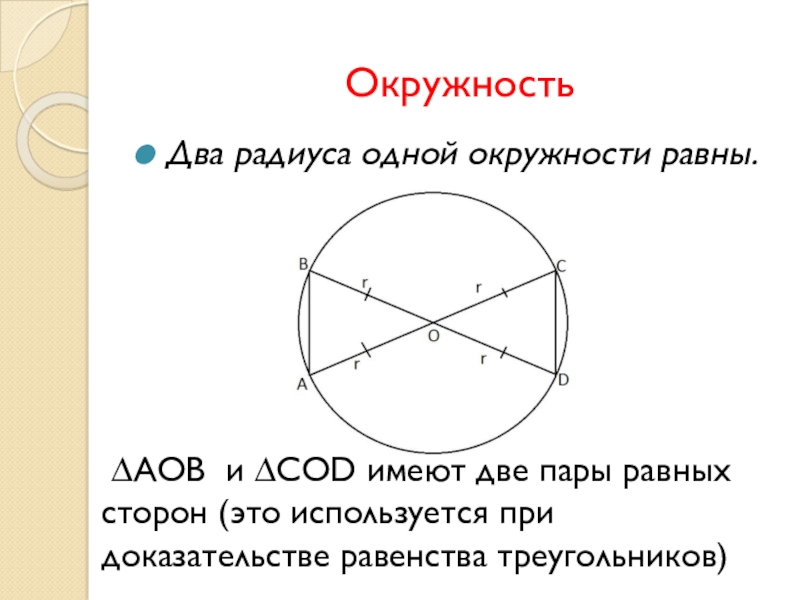
Окружность
Два радиуса одной окружности равны.
∆АОВ и ∆СОD имеют
две пары равных сторон (это используется при доказательстве равенства треугольников)
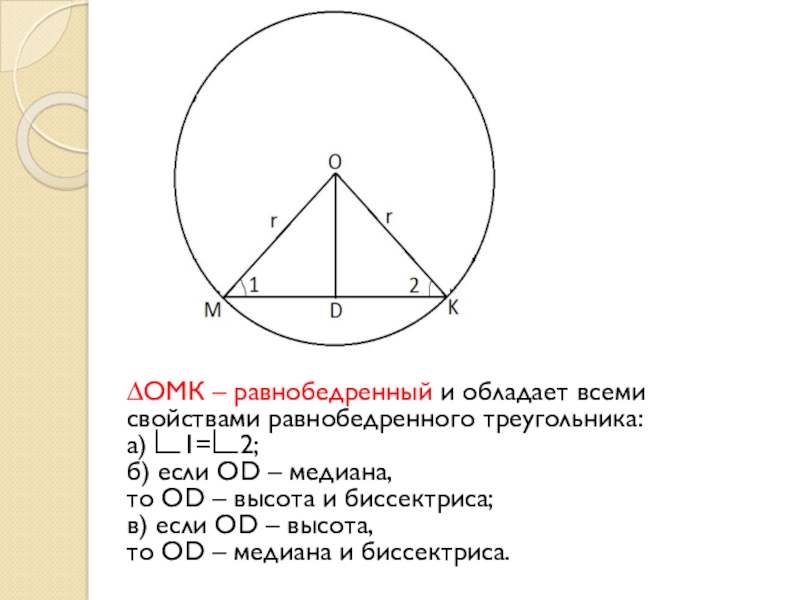
Слайд 6∆ОМК – равнобедренный и обладает всеми свойствами равнобедренного треугольника:
а) ∟1=∟2;
б) если
OD – медиана,
то OD – высота и биссектриса;
в) если OD – высота,
то OD – медиана и биссектриса.
то OD – высота и биссектриса;
в) если OD – высота,
то OD – медиана и биссектриса.
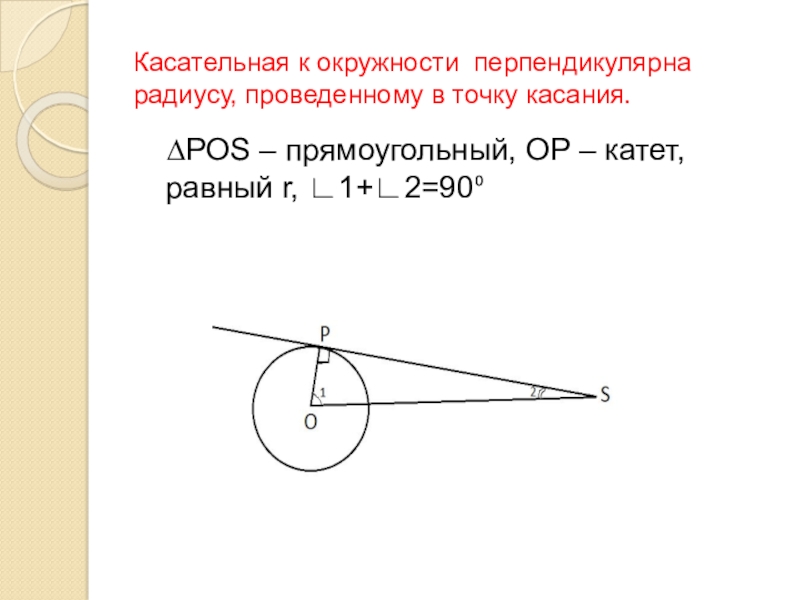
Слайд 7Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
∆POS
– прямоугольный, OP – катет, равный r, ∟1+∟2=90⁰
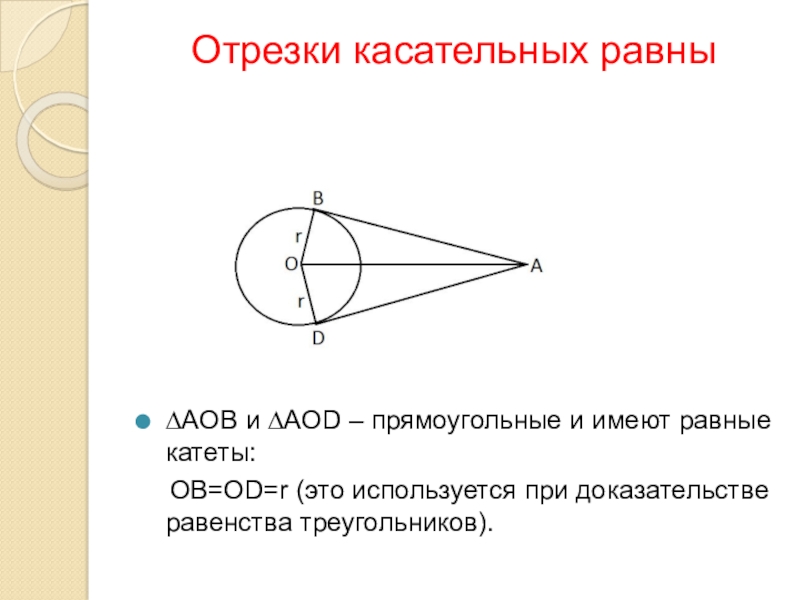
Слайд 8Отрезки касательных равны
∆AOB и ∆AOD – прямоугольные и имеют равные катеты:
OB=OD=r (это используется при доказательстве равенства треугольников).
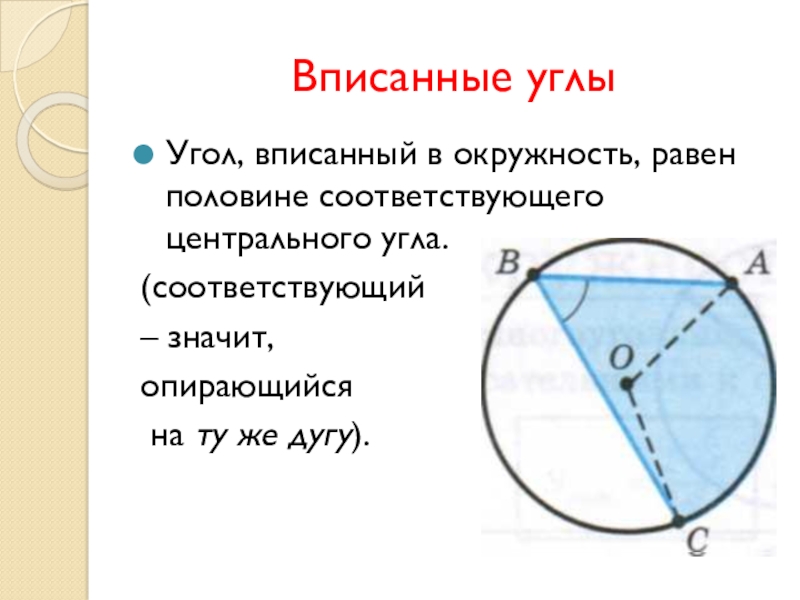
Слайд 10Вписанные углы
Угол, вписанный в окружность, равен половине соответствующего центрального угла.
(соответствующий
–
значит,
опирающийся
на ту же дугу).
опирающийся
на ту же дугу).
Слайд 13Многоугольник
1. В выпуклом многоугольнике:
сумма углов равна 180⁰*(n-2),
где
n – число его вершин(сторон).
Например:
сумма углов треугольника равна 180⁰*(3-2)=180⁰,
сумма углов пятиугольника равна 180⁰*(5-2)=540⁰.
Например:
сумма углов треугольника равна 180⁰*(3-2)=180⁰,
сумма углов пятиугольника равна 180⁰*(5-2)=540⁰.
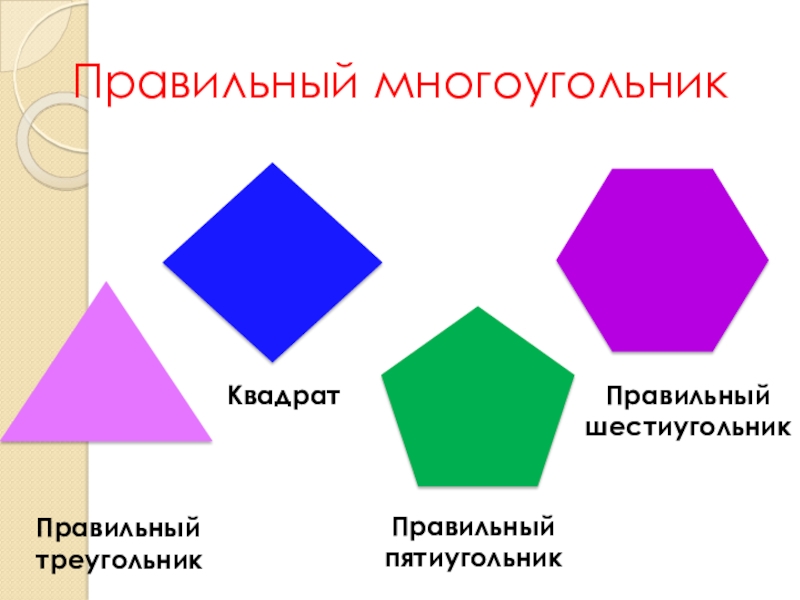
Слайд 14Правильный многоугольник
Правильный
треугольник
Квадрат
Правильный
пятиугольник
Правильный
шестиугольник
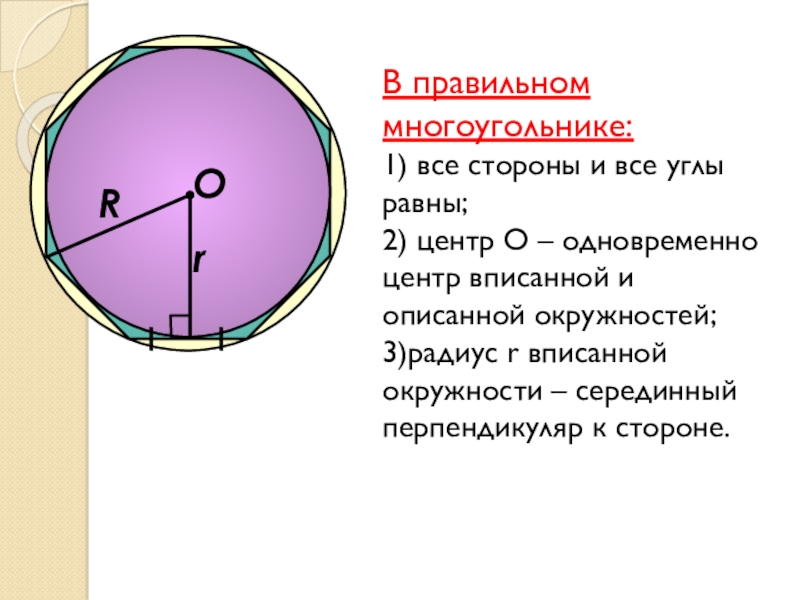
Слайд 15О
R
r
В правильном многоугольнике:
1) все стороны и все углы равны;
2) центр О
– одновременно центр вписанной и описанной окружностей;
3)радиус r вписанной окружности – серединный перпендикуляр к стороне.
3)радиус r вписанной окружности – серединный перпендикуляр к стороне.
Слайд 16При решении задач часто бывает полезно находить элементы прямоугольного треугольника АОМ,
сторонами которого являются:
ОА – радиус описанной окружности,
ОМ – радиус вписанной окружности,
АМ – половина стороны правильного многоугольника.
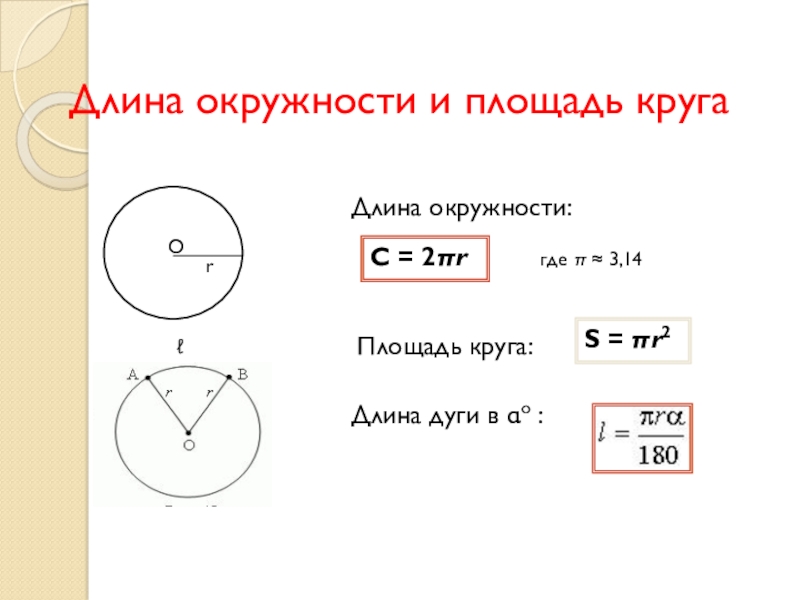
Слайд 17Длина окружности и площадь круга
О
r
Длина окружности:
Длина
дуги в αo :
C = 2πr
где π ≈ 3,14
ℓ
Площадь круга:
S = πr2