- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Взаимное расположение прямых. Угол между прямыми (10 класс)
Содержание
- 1. Презентация по геометрии на тему Взаимное расположение прямых. Угол между прямыми (10 класс)
- 2. Как известно… Как известно из курса планиметрии,
- 3. определение Две прямые называются скрещивающимися, если они не лежат в одной плоскости
- 4. Теорема «Признак скрещивающихся прямых» Если одна
- 5. доказательствоРассмотрим прямую AB лежащую в плоскости и
- 6. В пространстве прямые расположены следующим образом:
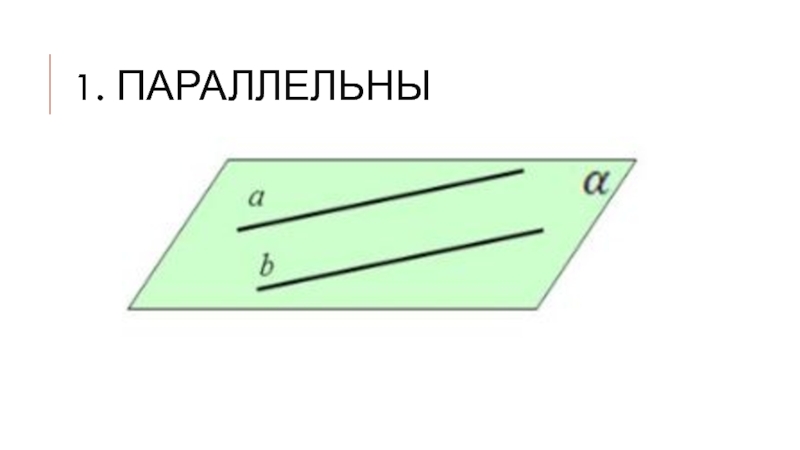
- 7. 1. Параллельны
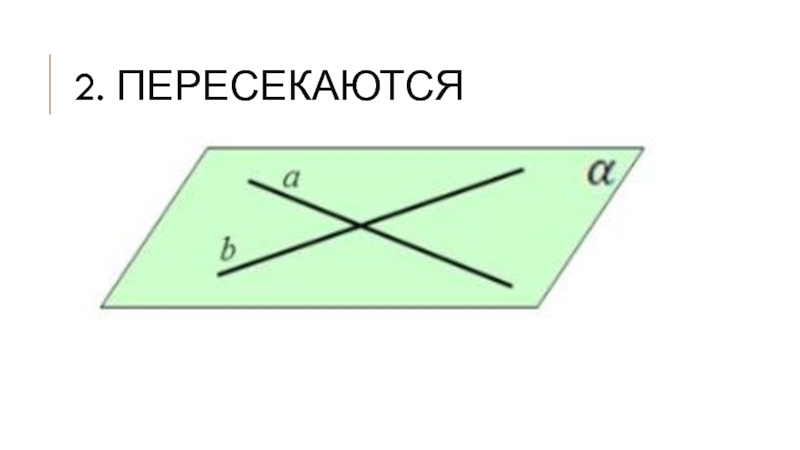
- 8. 2. пересекаются
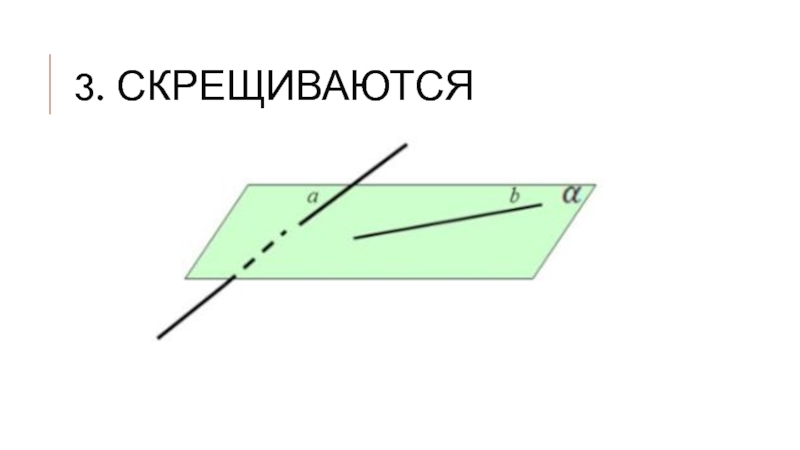
- 9. 3. Скрещиваются
- 10. теорема Через каждую из двух скрещивающихся
- 11. доказательствоРассмотрим скрещивающиеся прямые AB и CD. Через
- 12. Углы между прямымиЕсли прямые параллельны, то угол
- 13. СПАСИБО ЗА ВНИМАНИЕ
Как известно… Как известно из курса планиметрии, две прямые в плоскости могут пересекаться (имеют общую точку) или быть параллельными (не имеют общую точку)
Слайд 1Взаимное расположение прямых в пространстве. Угол между прямыми
Учитель математики:
Тотикова Елена Сосланбековна
Слайд 2Как известно…
Как известно из курса планиметрии, две прямые в плоскости
могут пересекаться (имеют общую точку) или быть параллельными (не имеют общую точку)
Слайд 4Теорема «Признак скрещивающихся прямых»
Если одна из двух прямых лежит
в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются (не лежат в одной плоскости).
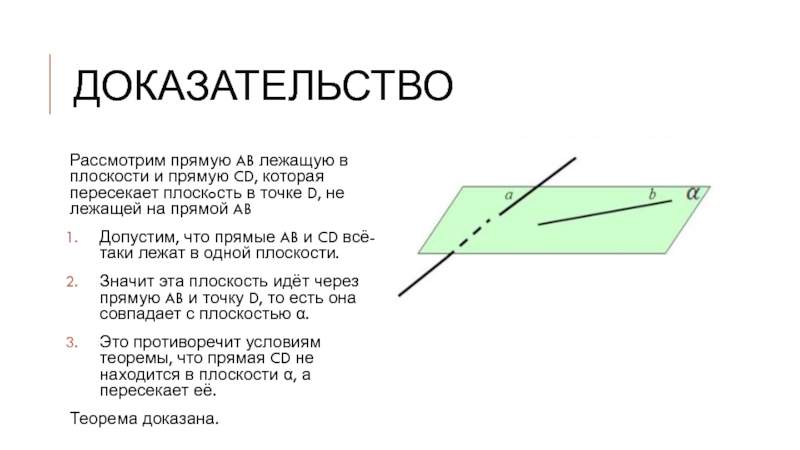
Слайд 5доказательство
Рассмотрим прямую AB лежащую в плоскости и прямую CD, которая пересекает
плоскoсть в точке D, не лежащей на прямой AB
Допустим, что прямые AB и CD всё-таки лежат в одной плоскости.
Значит эта плоскость идёт через прямую AB и точку D, то есть она совпадает с плоскостью α.
Это противоречит условиям теоремы, что прямая CD не находится в плоскости α, а пересекает её.
Теорема доказана.
Допустим, что прямые AB и CD всё-таки лежат в одной плоскости.
Значит эта плоскость идёт через прямую AB и точку D, то есть она совпадает с плоскостью α.
Это противоречит условиям теоремы, что прямая CD не находится в плоскости α, а пересекает её.
Теорема доказана.
Слайд 10теорема
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная
другой прямой, и притом только одна
Слайд 11доказательство
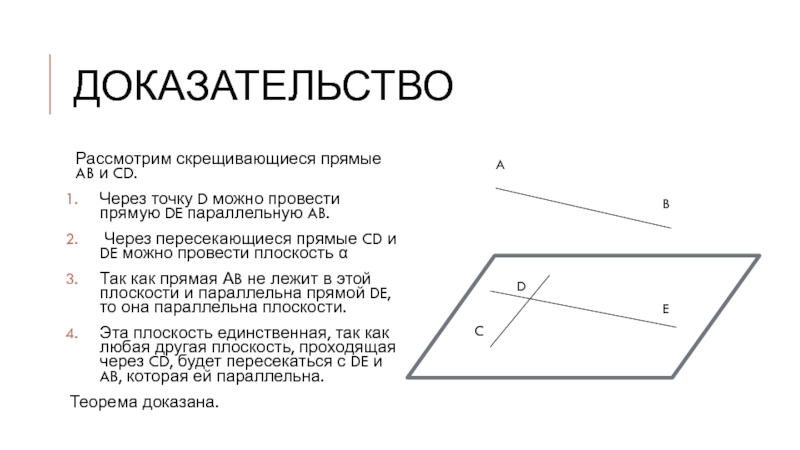
Рассмотрим скрещивающиеся прямые AB и CD.
Через точку D можно провести
прямую DE параллельную AB.
Через пересекающиеся прямые CD и DE можно провести плоскость α
Так как прямая АB не лежит в этой плоскости и параллельна прямой DE, то она параллельна плоскости.
Эта плоскость единственная, так как любая другая плоскость, проходящая через CD, будет пересекаться с DE и AB, которая ей параллельна.
Теорема доказана.
Через пересекающиеся прямые CD и DE можно провести плоскость α
Так как прямая АB не лежит в этой плоскости и параллельна прямой DE, то она параллельна плоскости.
Эта плоскость единственная, так как любая другая плоскость, проходящая через CD, будет пересекаться с DE и AB, которая ей параллельна.
Теорема доказана.
A
B
C
D
E
Слайд 12Углы между прямыми
Если прямые параллельны, то угол между ними 0 градусов.
Углом между двумя пересекающимися прямыми называют величину меньшего из углов, образованных этими прямыми. Если все углы равны, то эти прямые перпендикулярны (образуют угол 90 градусов).
Углом между двумя скрещивающимися прямыми называют угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимися прямым.