- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Второй признак равенства треугольников
Содержание
- 1. Презентация по геометрии на тему Второй признак равенства треугольников
- 2. Какая фигура называется треугольником? Какие треугольники называются
- 3. Первый признак равенства треугольников.Если две стороны и
- 4. Второй признак равенства треугольников.Если сторона и два
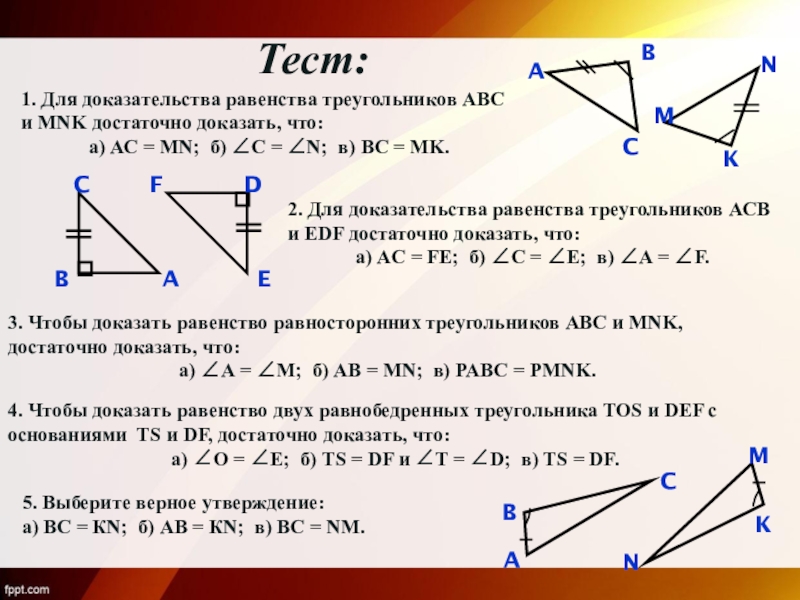
- 5. Тест:1. Для доказательства равенства треугольников АВС и
- 6. Ответы:1.в)2.б)3.б)4.б)5.а)
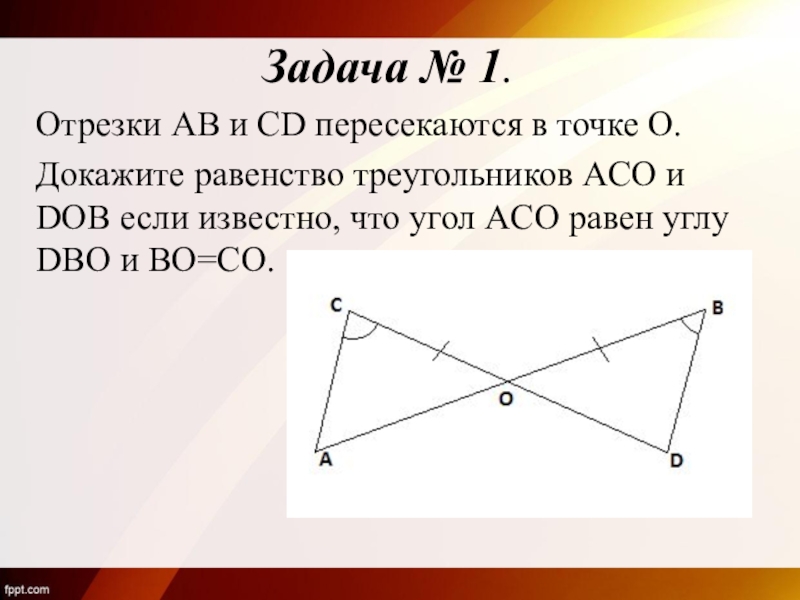
- 7. Задача № 1. Отрезки AB и CD
- 8. Решение:Рассмотрим ∆ ACO и ∆ DBO:BO=CO (по условию)
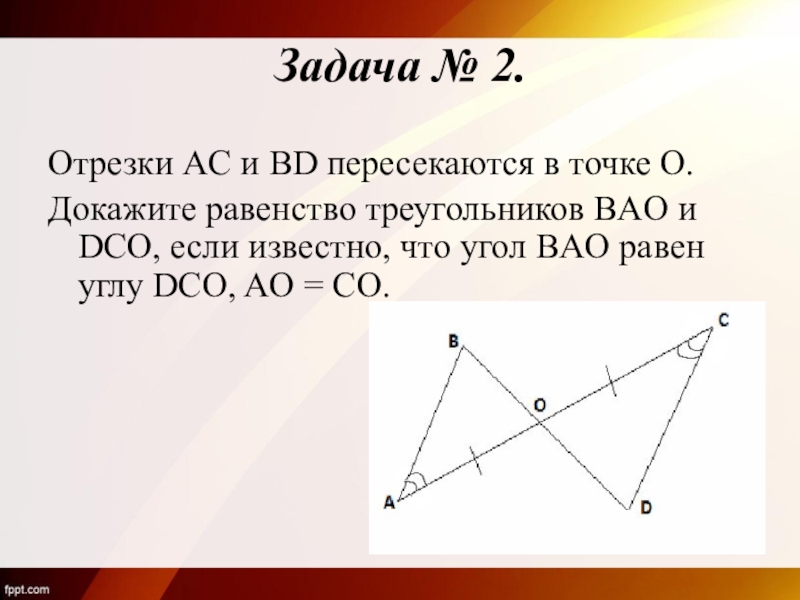
- 9. Отрезки AC и BD пересекаются в точке
- 10. Решение:Рассмотрим ∆ BAO и ∆ DCO.AO = CO (по условию)
- 11. № 130А1АВСОО1В1С1Дано: ∆АВС и ∆А1В1С1
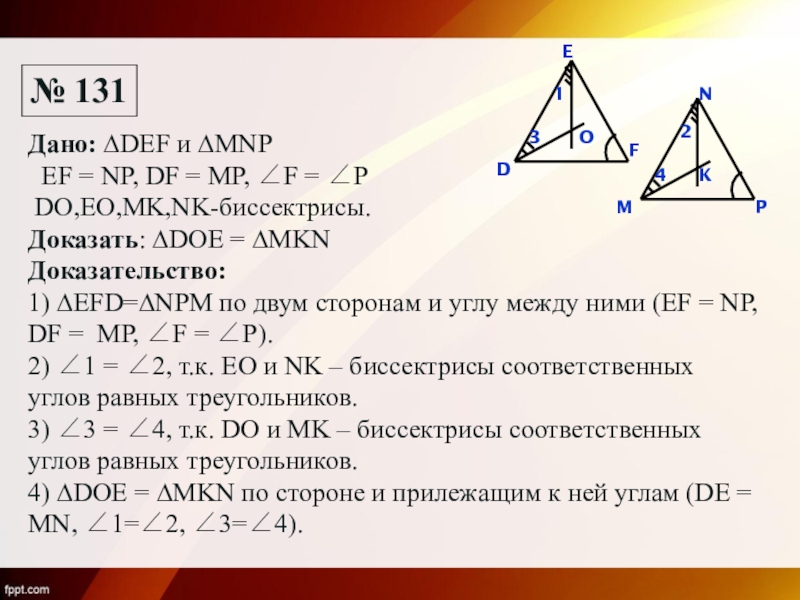
- 12. № 131DEFOMNPKДано: ∆DEF и ∆MNP EF =
- 13. № 133Дано: ∆АВС BD – биссектриса
- 14. № 1№ 2BАCD12 Дано: BD – биссектриса
- 15. №1 Дано: BD-биссектриса ∠ABC, ∠1=∠2. Доказать: AB=CB
- 16. №2 Дано: О-середина AB, ∠1=∠2. Доказать: ∠C=∠D.
- 17. «Геометрия является самым могущественным средством для
- 18. Домашнее задание Решите задачи №128, 129, 132, 134.
Слайд 2Какая фигура называется треугольником?
Какие треугольники называются равными?
Как можно узнать, равны ли
Какие элементы достаточно рассмотреть для доказательства равенства треугольников?
Слайд 3Первый признак равенства треугольников.
Если две стороны и угол между ними одного
Слайд 4Второй признак равенства треугольников.
Если сторона и два прилежащие к ней угла
Слайд 5Тест:
1. Для доказательства равенства треугольников АВС и MNK достаточно доказать, что:
а)
2. Для доказательства равенства треугольников АСВ и EDF достаточно доказать, что:
а) AC = FE; б) ∠C = ∠E; в) ∠A = ∠F.
3. Чтобы доказать равенство равносторонних треугольников АВС и MNK, достаточно доказать, что:
а) ∠А = ∠М; б) АВ = МN; в) PABC = PMNK.
4. Чтобы доказать равенство двух равнобедренных треугольника TOS и DEF с основаниями TS и DF, достаточно доказать, что:
а) ∠О = ∠Е; б) TS = DF и ∠Т = ∠D; в) TS = DF.
5. Выберите верное утверждение:
а) ВС = КN; б) АВ = КN; в) ВС = NM.
C
A
B
K
N
M
A
B
C
F
D
E
A
B
C
M
N
K
Слайд 7Задача № 1.
Отрезки AB и CD пересекаются в точке O.
Докажите равенство
Слайд 8Решение:
Рассмотрим ∆ ACO и ∆ DBO:
BO=CO (по условию)
Слайд 9Отрезки AC и BD пересекаются в точке O.
Докажите равенство треугольников BAO
Задача № 2.
Слайд 10Решение:
Рассмотрим ∆ BAO и ∆ DCO.
AO = CO (по условию)
Слайд 11№ 130
А1
А
В
С
О
О1
В1
С1
Дано: ∆АВС и ∆А1В1С1
СО и С1О1-
ВС = В1С1, ∠В = ∠В1
∠С = ∠С1
Доказать:1)∆АСО=∆А1С1О1
2)∆ВСО=∆В1С1О1
Доказательство: 1) ∆АВС = ∆А1В1С1 по стороне и прилежащим к ней углам (ВС = В1С1, ∠В=∠В1, ∠С = ∠С1).
2) ВО = ОА = В1О1 = О1А1,
т.к. СО и С1О1 – медианы равных треугольников. 3) АС = А1С1, ∠А = ∠А1, т.к. ∆АВС = ∆А1В1С1. АО = А1О1 ⇒ ∆ВСО=∆В1С1О1
Слайд 12№ 131
D
E
F
O
M
N
P
K
Дано: ∆DEF и ∆MNP
EF = NP, DF = MP,
DO,EO,MK,NK-биссектрисы. Доказать: ∆DOE = ∆MKN
Доказательство: 1) ∆EFD=∆NPM по двум сторонам и углу между ними (EF = NP, DF = MP, ∠F = ∠P).
2) ∠1 = ∠2, т.к. ЕО и NK – биссектрисы соответственных углов равных треугольников.
3) ∠3 = ∠4, т.к. DO и MK – биссектрисы соответственных углов равных треугольников.
4) ∆DOE = ∆MKN по стороне и прилежащим к ней углам (DE = MN, ∠1=∠2, ∠3=∠4).
1
3
2
4
Слайд 13№ 133
Дано: ∆АВС
BD – биссектриса и высота
Доказать:
∆АВС
А
В
С
D
Доказательство:
BD – биссектриса ∆АВС
∆АВD = ∆CBD по стороне и прилежащим к ней углам (BD общая, ∠ABD = ∠CBD, ∠ADB = ∠CDB).
АВ = ВС как соответственные стороны равных треугольников.
Т.к. АВ = ВС, то ∆АВС – равнобедренный.
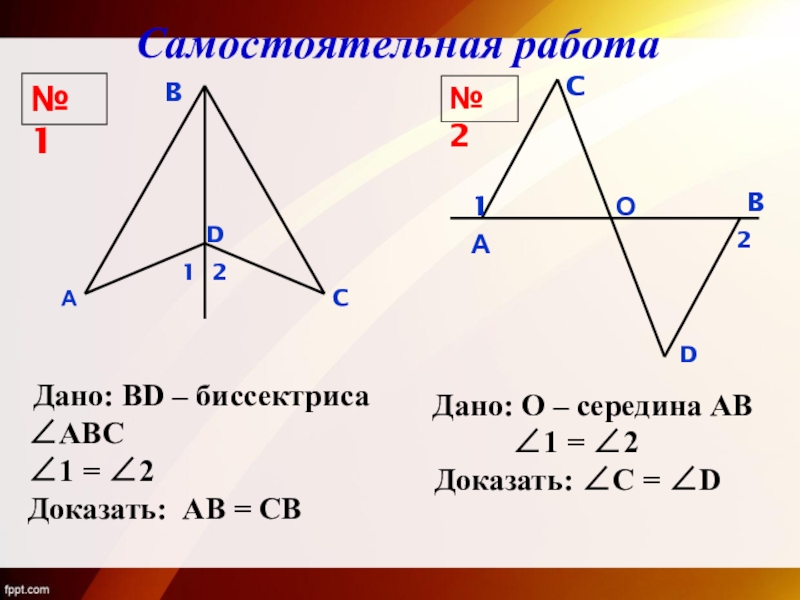
Слайд 14№ 1
№ 2
B
А
C
D
1
2
Дано: BD – биссектриса ∠АВС
∠1 = ∠2
Доказать:
А
B
C
D
1
2
Дано: О – середина АВ
∠1 = ∠2
Доказать: ∠С = ∠D
О
Самостоятельная работа
Слайд 15№1 Дано: BD-биссектриса ∠ABC, ∠1=∠2. Доказать: AB=CB Доказательство: BD- биссектриса ∆ABC, поэтому ∠ABD=∠CBD. ∠1=∠2,
Решение:
Слайд 16№2 Дано: О-середина AB, ∠1=∠2. Доказать: ∠C=∠D. Доказательство: О-середина AB, значит, АО=ВО. ∆ACO=∆DBO по стороне
Решение:
Слайд 17 «Геометрия является самым могущественным средством для изощрения наших умственных способностей
Галилео Галилей