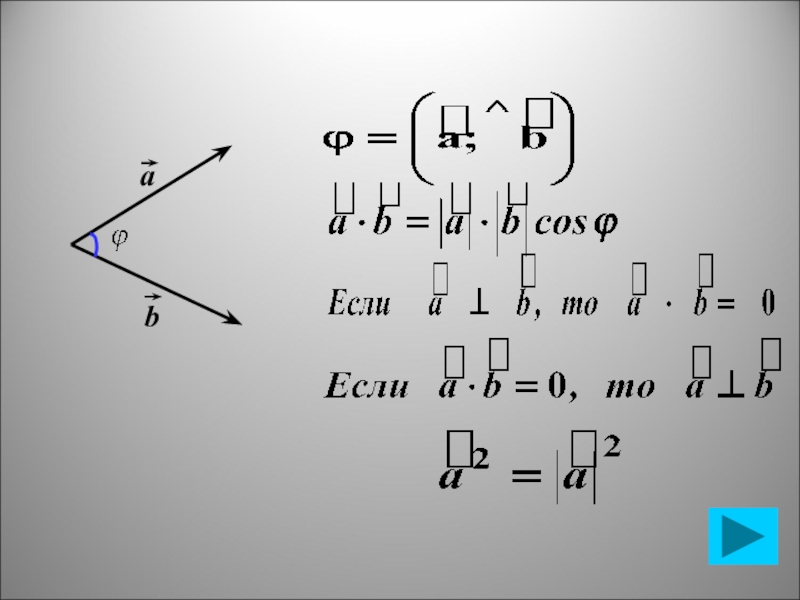Технологический колледж 34
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Векторы в пространстве
Содержание
- 1. Презентация по геометрии на тему Векторы в пространстве
- 2. СодержаниеПонятие вектора. Равенство векторов.Сложение и вычитание векторов.
- 3. АВаОпределение вектораМодуль (длина) вектораСвойства нулевого вектораМ
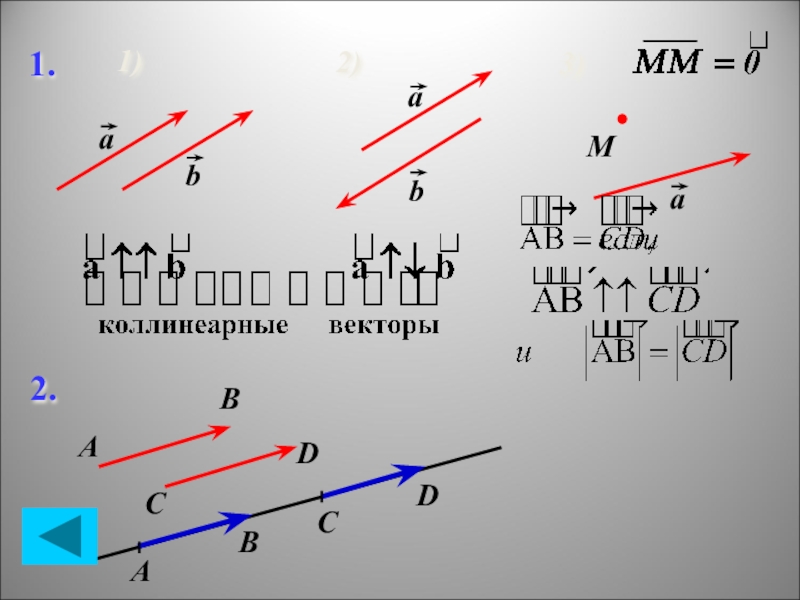
- 4. 1.1)2)3)МаааbbABCDABCD2.
- 5. аbABС АВ + ВС = АС (для любых трех точек А, В, и С)аbПравило параллелограммаПравило треугольникаА
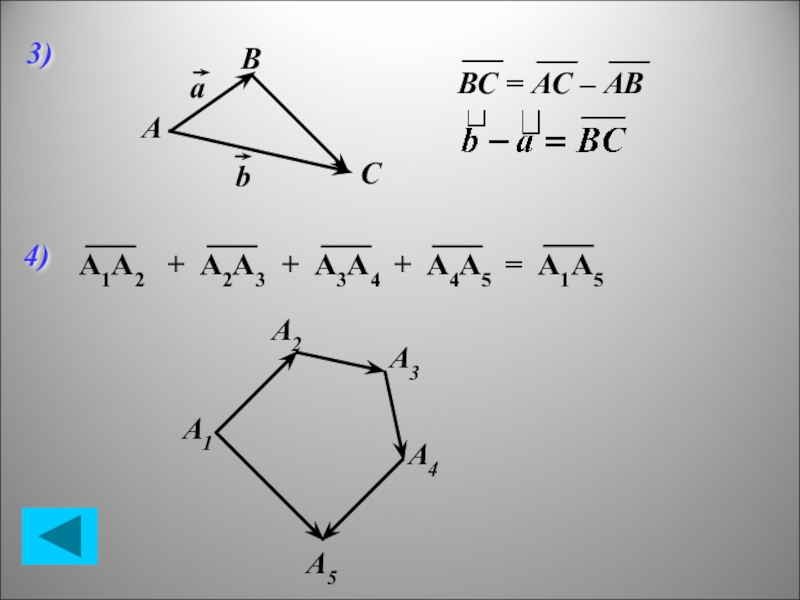
- 6. ABСаb3)ВС = АС – АВ 4)А1А2 + А2А3 + А3А4 + А4А5 = А1А5A1A2A3A4A5
- 7. Умножение вектора на число.ааСвойства:
- 8. Умножение вектора на число.аЛемма. b
- 9. Определение: Три вектора называются компланарными, если при
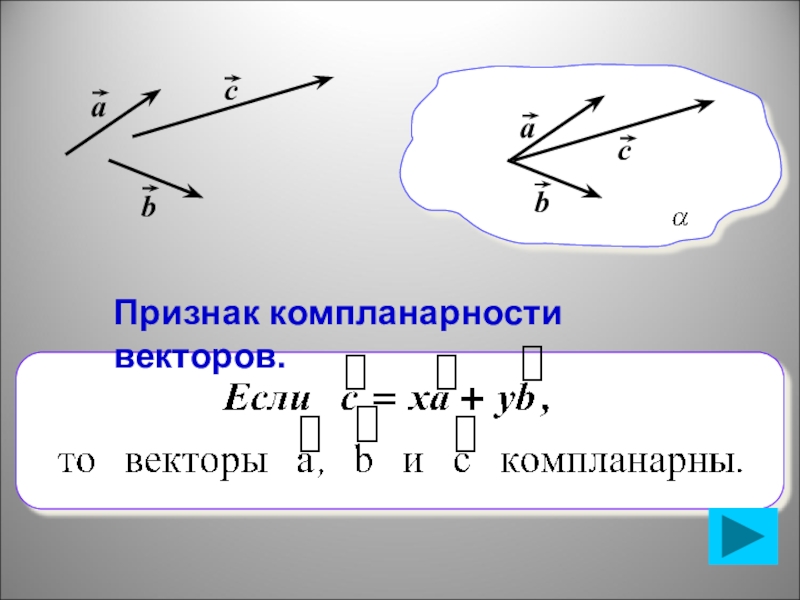
- 10. ааbbссПризнак компланарности векторов.
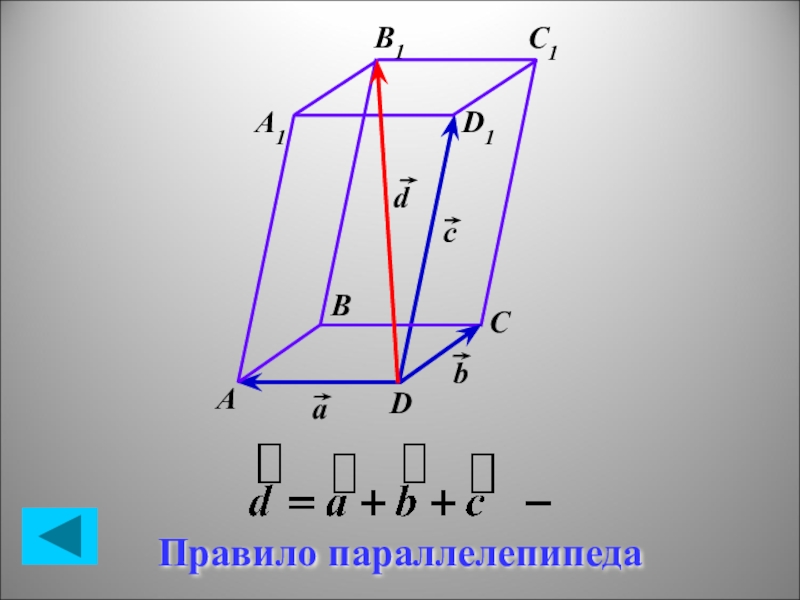
- 11. АDCC1В1А1D1ВbасdПравило параллелепипеда
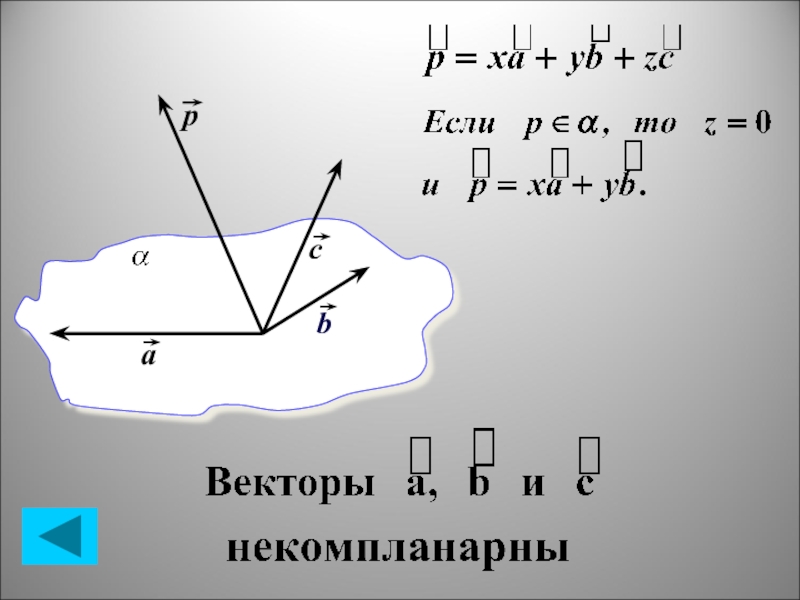
- 12. аbpс
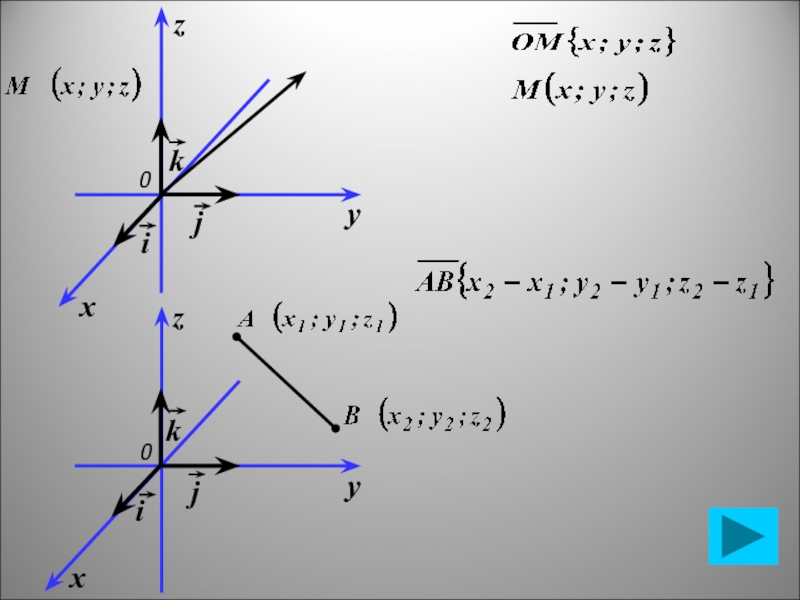
- 13. Метод координат в пространстве 0xyzkjia
- 14. y2)3)0xzkjia1)
- 15. 00xyzkjixyzkji
- 16. 0xyzkji
- 17. ab
- 18. Законы:
СодержаниеПонятие вектора. Равенство векторов.Сложение и вычитание векторов. Сумма нескольких векторов.Умножение вектора на число. Лемма о коллинеарных векторах.Компланарные векторы. Правило параллелепипеда.Разложение вектора по трем некомпланарным векторам.Метод координат в пространстве
Слайд 1Векторы и координаты в пространстве
Москалина Оксана Фёдоровна
Антонова Ольга Фёдоровна, преподаватели ГБПОУ
Слайд 2Содержание
Понятие вектора. Равенство векторов.
Сложение и вычитание векторов. Сумма нескольких векторов.
Умножение вектора
на число. Лемма о коллинеарных векторах.
Компланарные векторы. Правило параллелепипеда.
Разложение вектора по трем некомпланарным векторам.
Метод координат в пространстве
Компланарные векторы. Правило параллелепипеда.
Разложение вектора по трем некомпланарным векторам.
Метод координат в пространстве
Слайд 5а
b
A
B
С
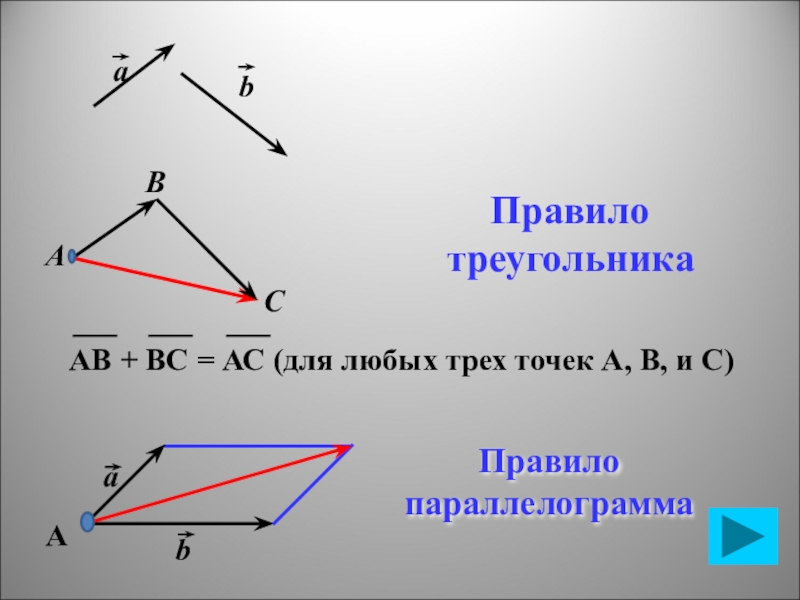
АВ + ВС = АС (для любых трех точек А,
В, и С)
а
b
Правило параллелограмма
Правило треугольника
А
Слайд 9Определение: Три вектора называются компланарными, если при откладывании их от одной
точки они лежат в одной плоскости.
Два вектора компланарны всегда.
Два вектора компланарны всегда.