- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Угол между прямыми
Содержание
- 1. Презентация по геометрии на тему Угол между прямыми
- 2. Цели урока:Рассмотреть формулировку и доказательство теоремы о
- 3. Повторение.Верно ли утверждение: если две прямые не
- 4. Любая прямая а, лежащая в плоскости, разделяет
- 5. Углы с сонаправленными сторонами.ОАО1А1Лучи ОА и О1А1
- 6. Теорема об углах с сонаправленными
- 7. Теорема об углах с сонаправленными
- 8. Теорема об углах с сонаправленными
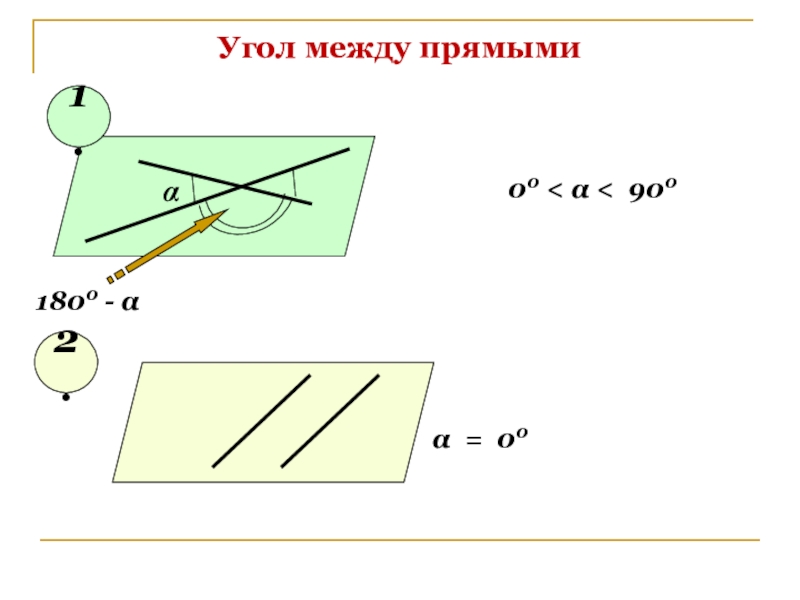
- 9. Угол между прямымиα1800 - α00 < α < 9001.2.α = 00
- 10. Угол между скрещивающимися прямыми. Угол между скрещивающимися
- 11. Дан куб АВСDА1В1С1D1.Найдите угол между прямыми:1.ВС и СС12.900АС и ВС4503.D1С1 и ВС9004.А1В1 и АС450
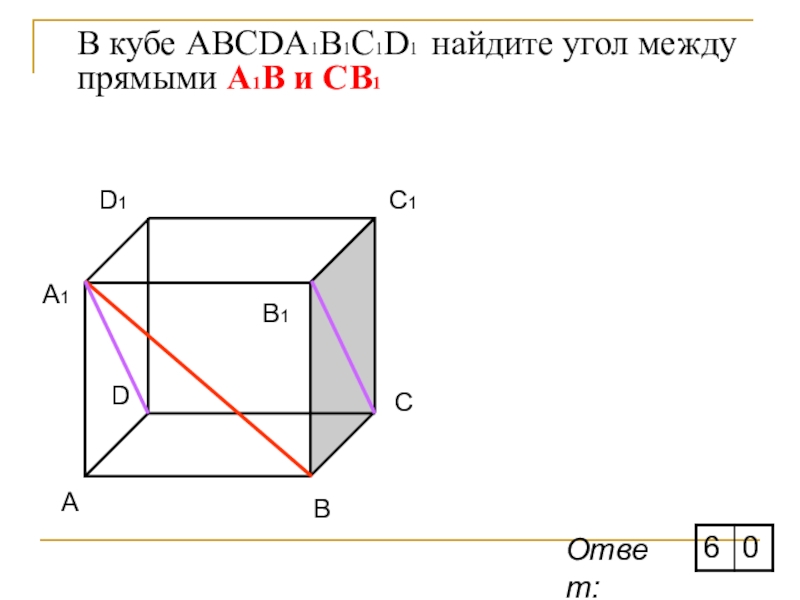
- 12. В кубе ABCDA1B1C1D1 найдите угол между прямыми А1В и CB1AОтвет:
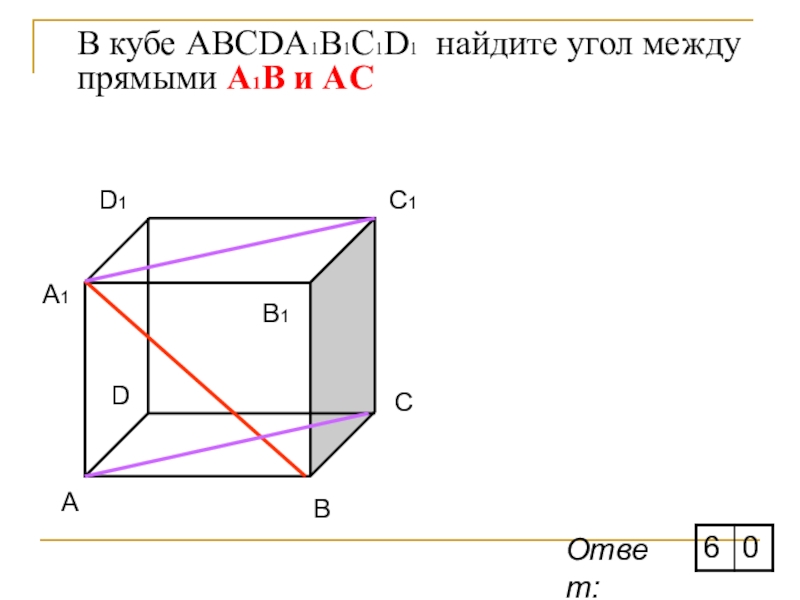
- 13. В кубе ABCDA1B1C1D1 найдите угол между прямыми А1В и ACAОтвет:
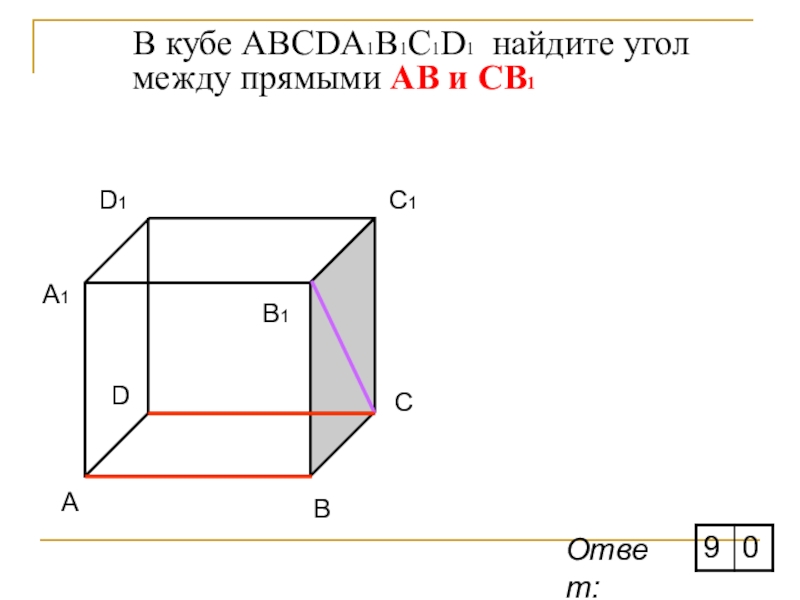
- 14. В кубе ABCDA1B1C1D1 найдите угол между прямыми АВ и CB1ACBDAA1D1C1B1Ответ:
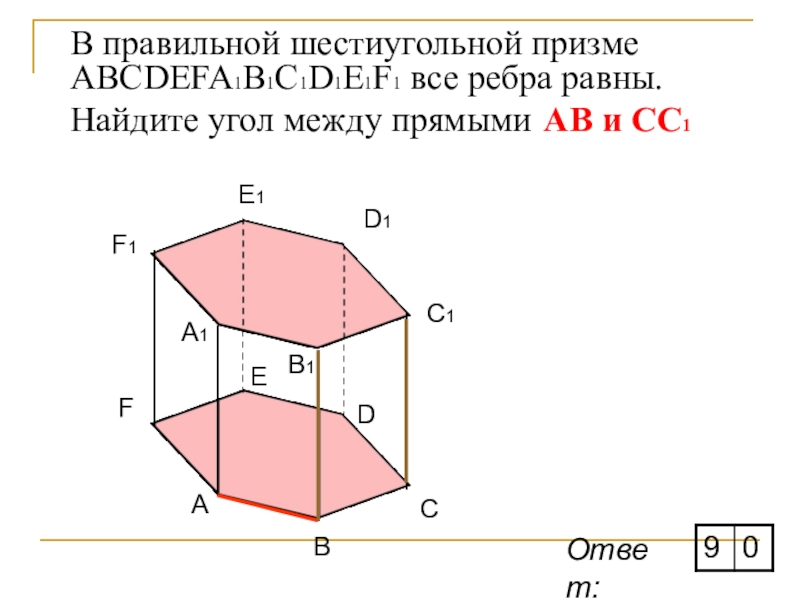
- 15. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны. Найдите угол между прямыми АВ и CС1ABCDEFA1F1E1D1C1B1Ответ:
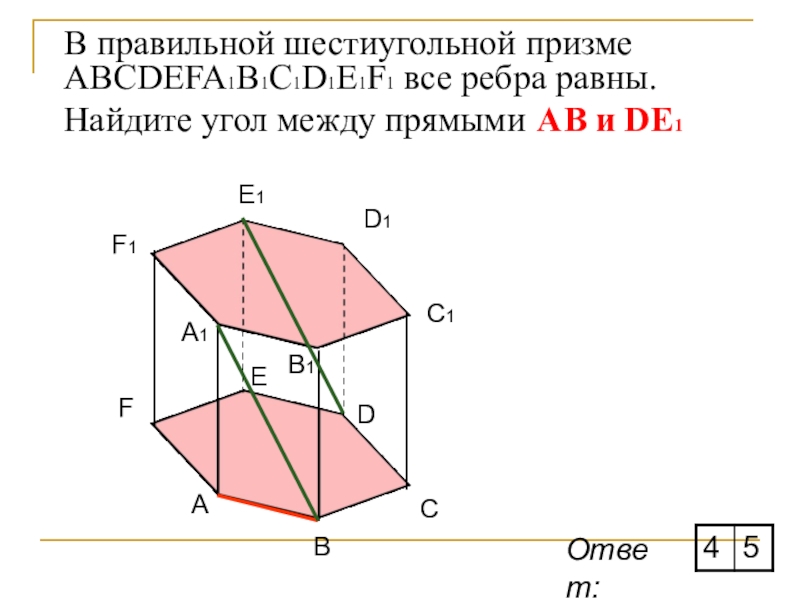
- 16. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны. Найдите угол между прямыми АВ и DE1ABCDEFA1F1E1D1C1B1Ответ:
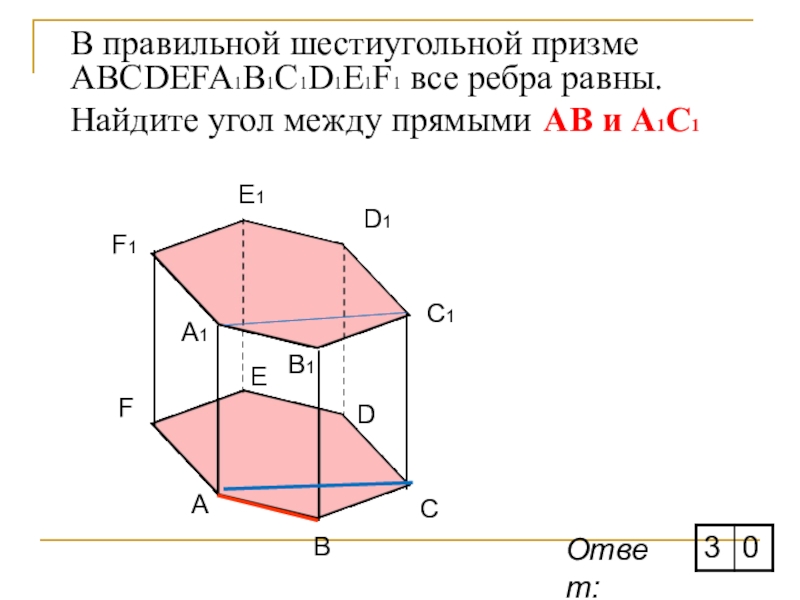
- 17. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны. Найдите угол между прямыми АВ и A1С1ABCDEFA1F1E1D1C1B1Ответ:
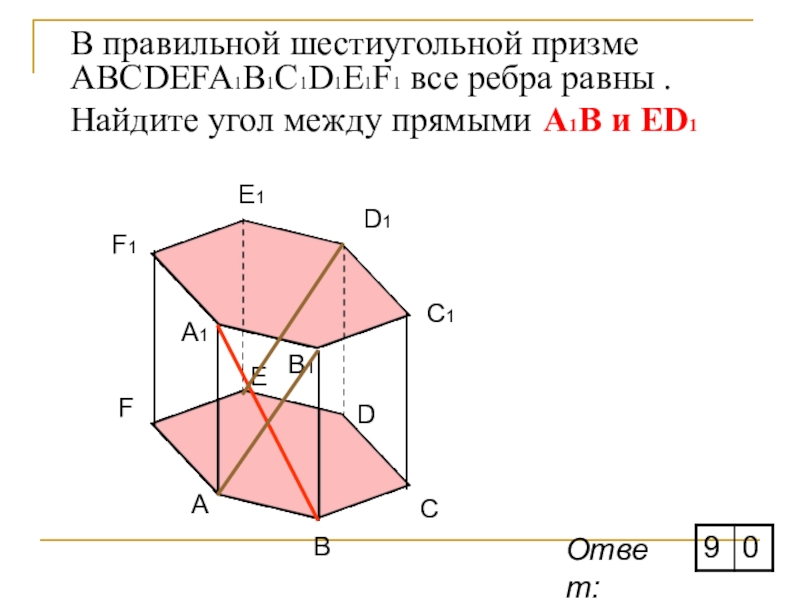
- 18. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны . Найдите угол между прямыми А1В и ED1ABCDEFA1F1E1D1C1B1Ответ:
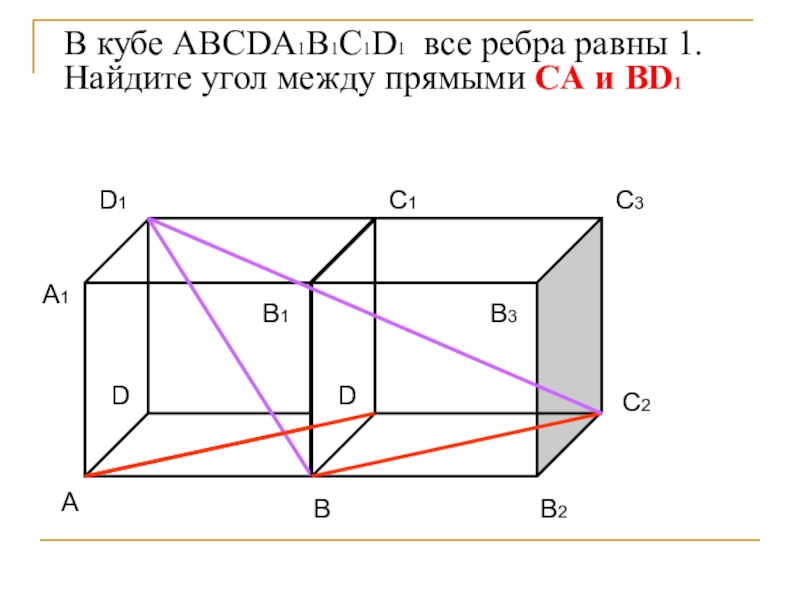
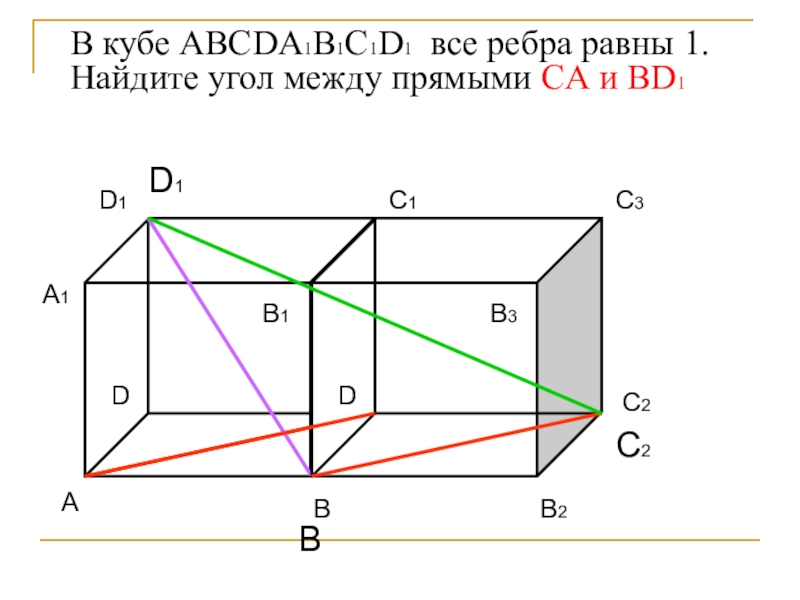
- 19. В кубе ABCDA1B1C1D1 все ребра равны 1. Найдите угол между прямыми CА и BD1
- 20. В кубе ABCDA1B1C1D1 все ребра равны 1. Найдите угол между прямыми CА и BD1BC2D1
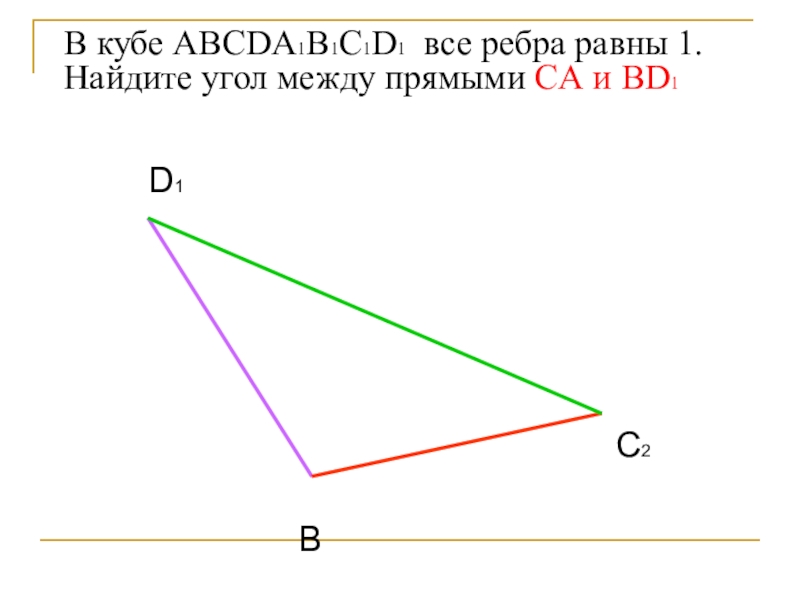
- 21. В кубе ABCDA1B1C1D1 все ребра равны 1. Найдите угол между прямыми CА и BD1BC2D1
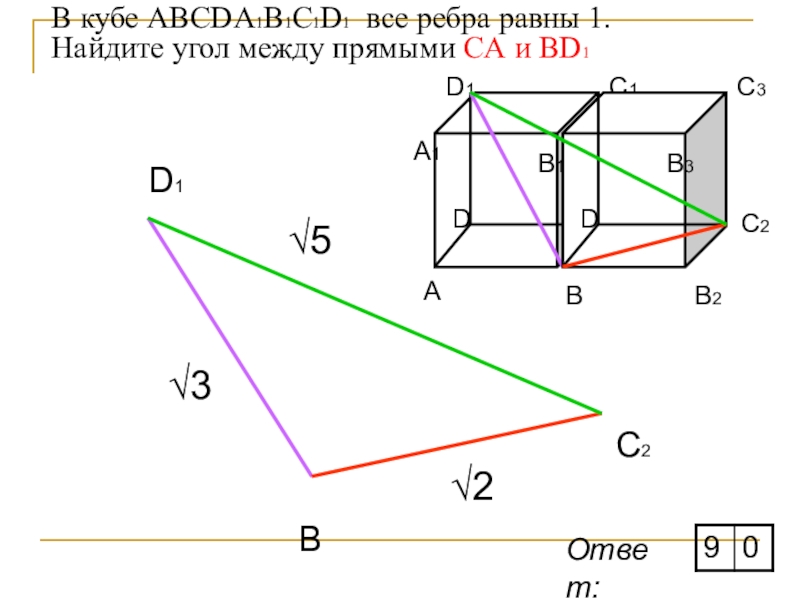
- 22. В кубе ABCDA1B1C1D1 все ребра равны 1. Найдите угол между прямыми CА и BD1BC2D1√2√3√5Ответ:
Слайд 2Цели урока:
Рассмотреть формулировку и доказательство теоремы о равенстве углов с сонаправленными
Научиться находить
угол между прямыми
в пространстве.
Слайд 3Повторение.
Верно ли утверждение: если две прямые не имеют общих точек, то
Две прямые параллельны некоторой плоскости. Могут ли эти прямые а) пресекаться?
б) быть скрещивающимися?
Могут ли скрещивающиеся прямые а и b быть параллельными прямой с?
Даны две скрещивающиеся прямые а и b. Точки А и А1 лежат на прямой а, точки В и В1 лежат на прямой b. Как будут расположены прямые АВ и А1В1?
Прямая а скрещивается с прямой b, а прямая b скрещивается с прямой с. Следует ли из этого, что прямые а и с - скрещиваются?
Нет
Да
Нет
Нет
Да
АВ скрещивается с А1В1
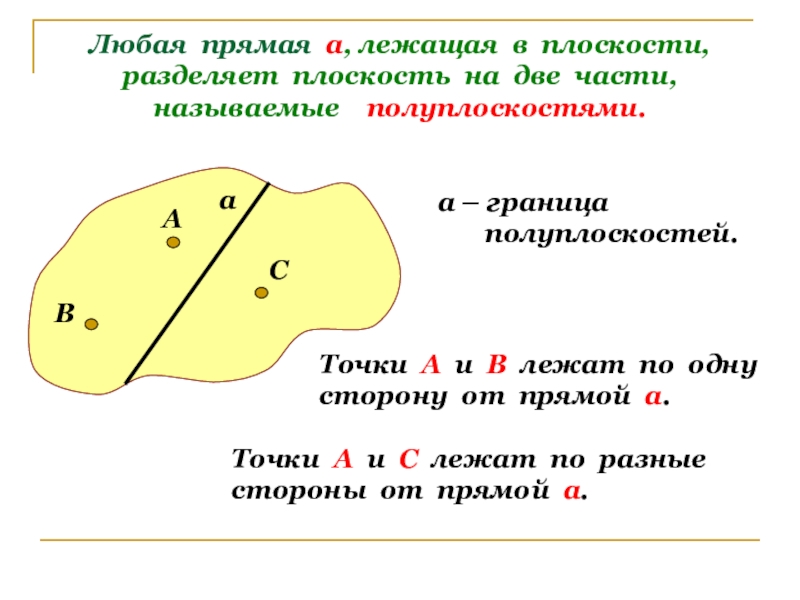
Слайд 4Любая прямая а, лежащая в плоскости, разделяет плоскость на две части,
а
а – граница
полуплоскостей.
А
В
С
Точки А и В лежат по одну
сторону от прямой а.
Точки А и С лежат по разные
стороны от прямой а.
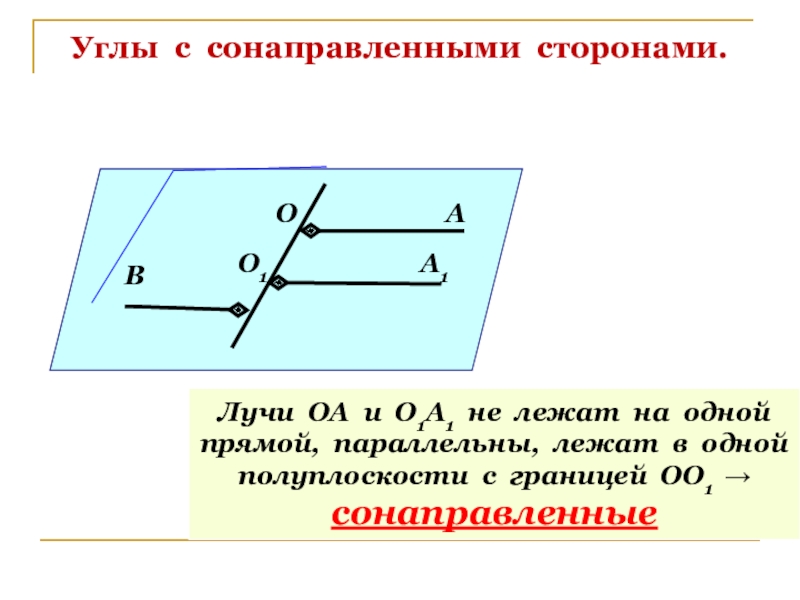
Слайд 5Углы с сонаправленными сторонами.
О
А
О1
А1
Лучи ОА и О1А1 не лежат на одной
прямой,
полуплоскости с границей ОО1 →
сонаправленные
В
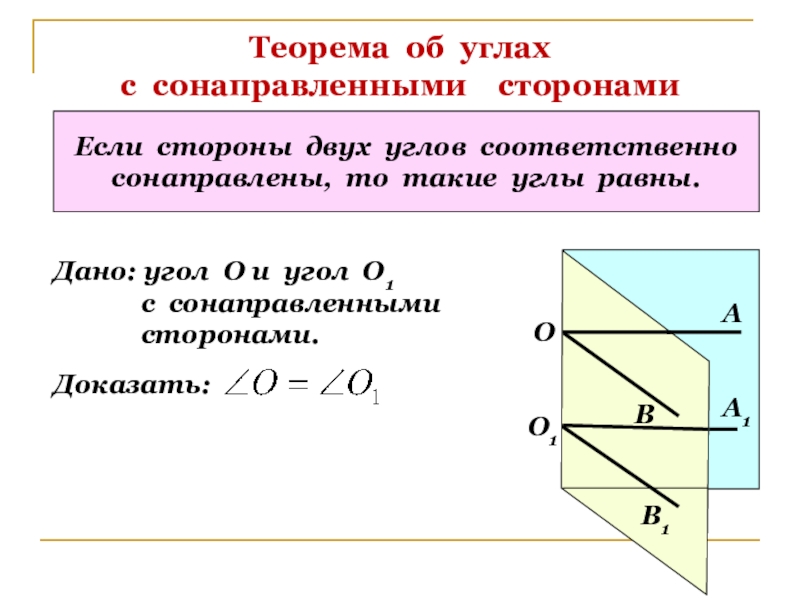
Слайд 6Теорема об углах
с сонаправленными сторонами
Если стороны двух углов соответственно
сонаправлены, то такие углы равны.
О1
О
А1
В1
В
А
Дано: угол О и угол О1
с сонаправленными
сторонами.
Доказать:
Слайд 7Теорема об углах
с сонаправленными сторонами
О1
О
А1
В1
В
А
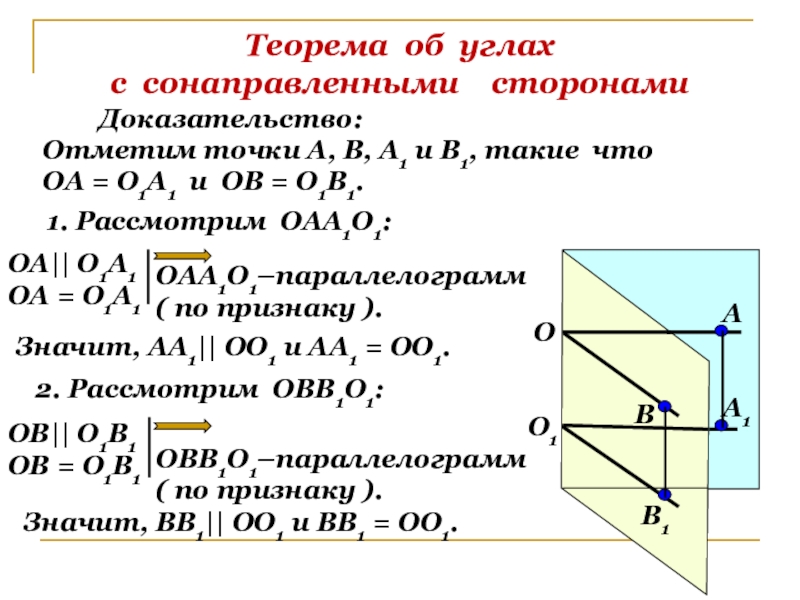
Доказательство:
Отметим точки А, В, А1
ОА = О1А1 и ОВ = О1В1.
1. Рассмотрим ОАА1О1:
ОА|| О1А1
ОА = О1А1
ОАА1О1–параллелограмм
( по признаку ).
2. Рассмотрим ОВВ1О1:
Значит, АА1|| ОО1 и АА1 = ОО1.
ОВ|| О1В1
ОВ = О1В1
ОВВ1О1–параллелограмм
( по признаку ).
Значит, ВВ1|| ОО1 и ВВ1 = ОО1.
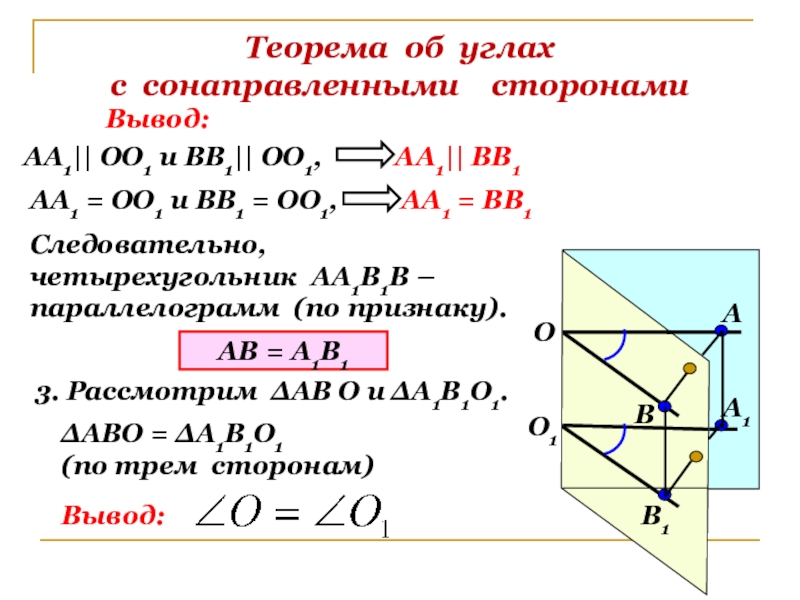
Слайд 8Теорема об углах
с сонаправленными сторонами
О1
О
А1
В1
В
А
Вывод:
АА1|| ОО1 и ВВ1|| ОО1,
АА1|| ВВ1
АА1 = ОО1 и ВВ1 = ОО1,
АА1 = ВВ1
Следовательно,
четырехугольник АА1В1В –
параллелограмм (по признаку).
АВ = А1В1
3. Рассмотрим ∆АВ О и ∆А1В1О1.
∆АВО = ∆А1В1О1
(по трем сторонам)
Вывод:
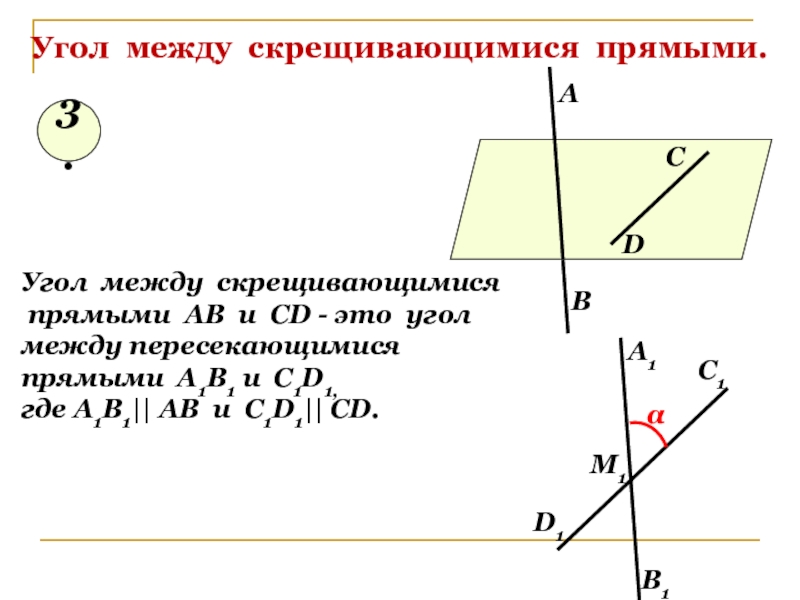
Слайд 10Угол между скрещивающимися прямыми.
Угол между скрещивающимися
прямыми АВ и
между пересекающимися
прямыми А1В1 и С1D1,
где А1В1|| АВ и С1D1|| CD.
А
В
D
С
А1
В1
С1
D1
α
М1
3.
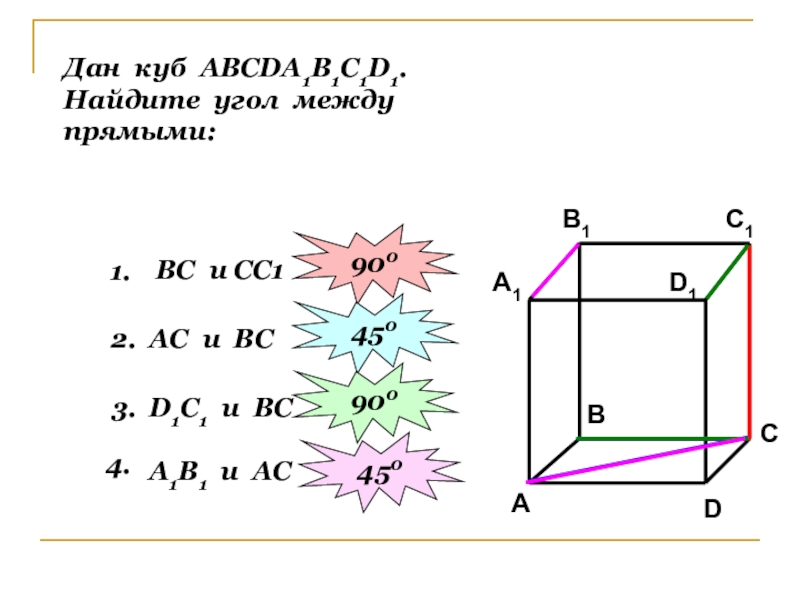
Слайд 11Дан куб АВСDА1В1С1D1.
Найдите угол между прямыми:
1.
ВС и СС1
2.
900
АС и ВС
450
3.
D1С1 и
900
4.
А1В1 и АС
450
Слайд 15В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны. Найдите угол между прямыми
A
B
C
D
E
F
A1
F1
E1
D1
C1
B1
Ответ:
Слайд 16В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны. Найдите угол между прямыми
A
B
C
D
E
F
A1
F1
E1
D1
C1
B1
Ответ:
Слайд 17В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны. Найдите угол между прямыми
A
B
C
D
E
F
A1
F1
E1
D1
C1
B1
Ответ:
Слайд 18В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны . Найдите угол между
A
B
C
D
E
F
A1
F1
E1
D1
C1
B1
Ответ: