:
«Трапеция»
учителя математики
ГБОУ школы №1056
Романенко Елены Алексеевны
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Трапеция
Содержание
- 1. Презентация по геометрии на тему Трапеция
- 2. Трапеция
- 3. Трапеция - это четырехугольник, у которого две стороны параллельны, а две другие не параллельны.BC || ADABCD
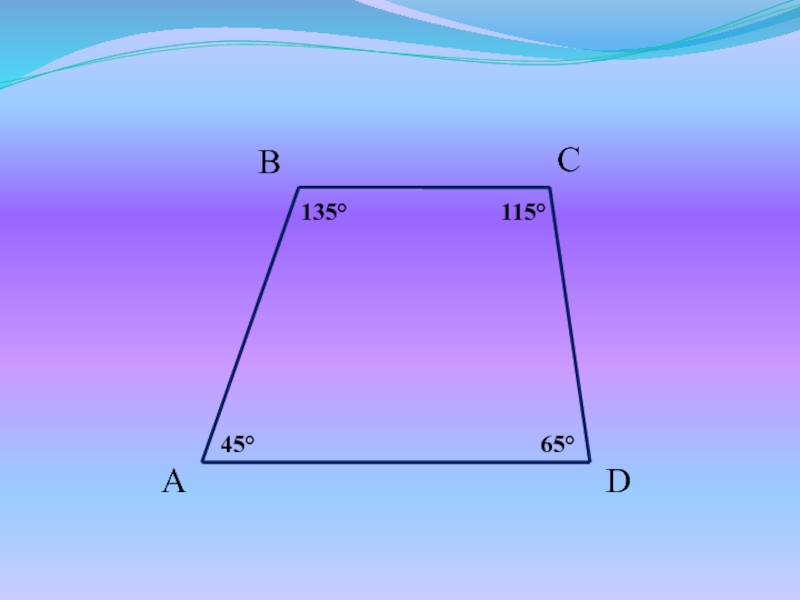
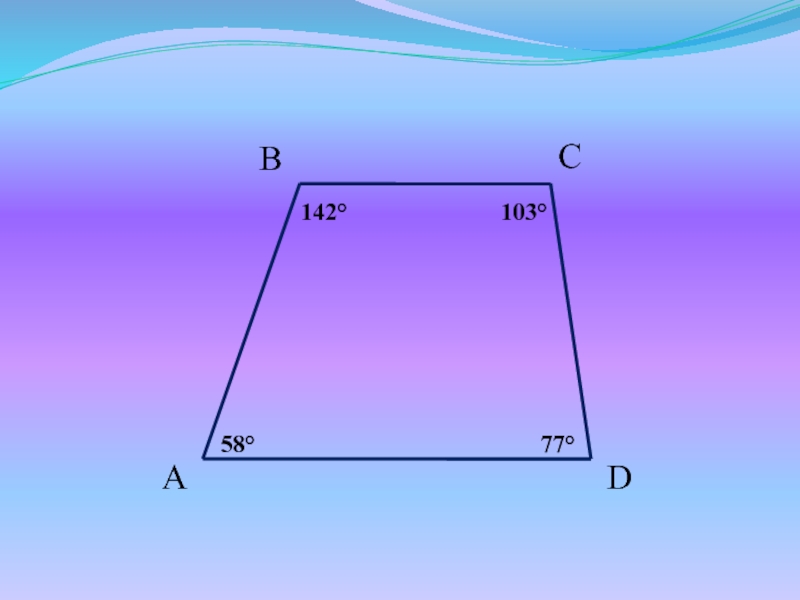
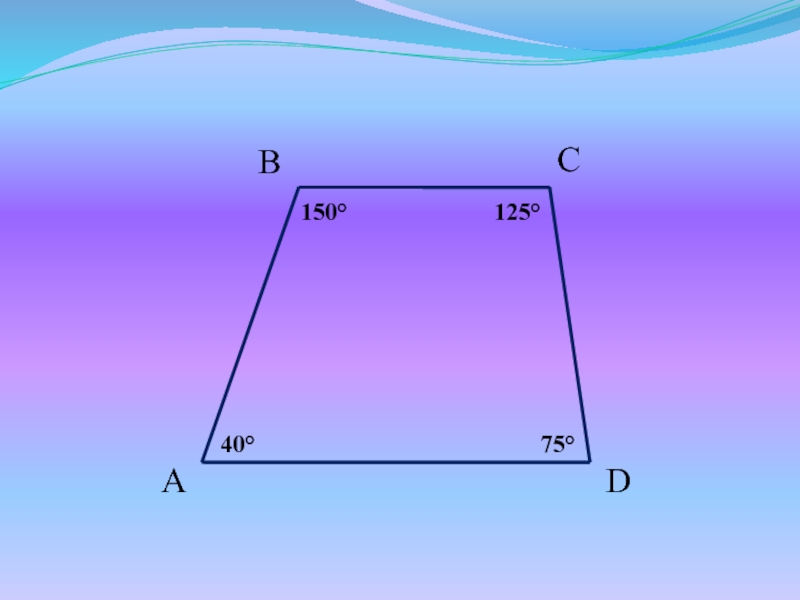
- 4. Задачи для устного решенияМогут ли у трапеции ABCD быть такие углы?
- 5. 1351154565
- 6. 1421035877
- 7. 1501254075
- 8. Равнобокая (равнобедренная) трапеция - это такая трапеция, у которой боковые стороны равны.BC || ADAB = CDABCD
- 9. Свойство равнобокой трапеции:У равнобокой трапеции углы при основании равныABCDКЕДано:ABCD – трапецияAB = CDДоказать:A = D
- 10. Доказательство:Проведем BK AD и CE
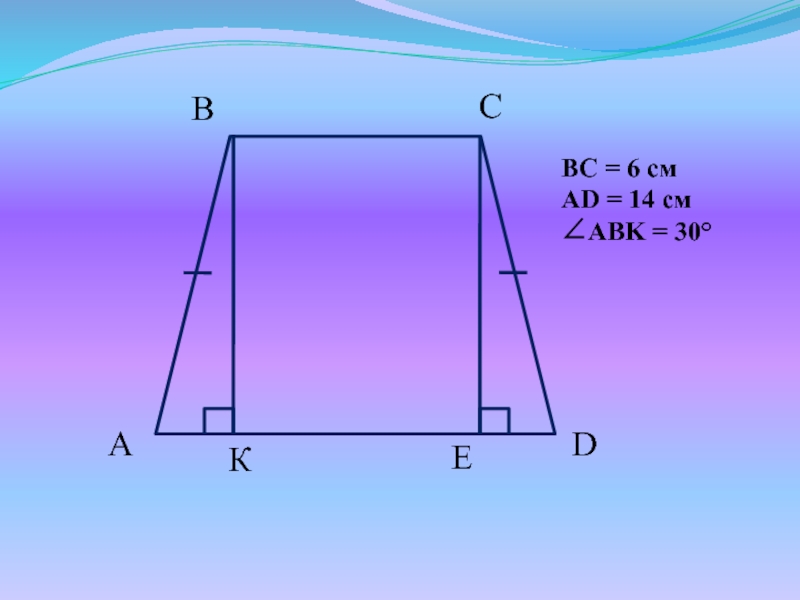
- 11. Задачи для устного решенияНайти периметр трапеции ABCD.
- 12. BC = 6 смAD = 14 смABK = 30
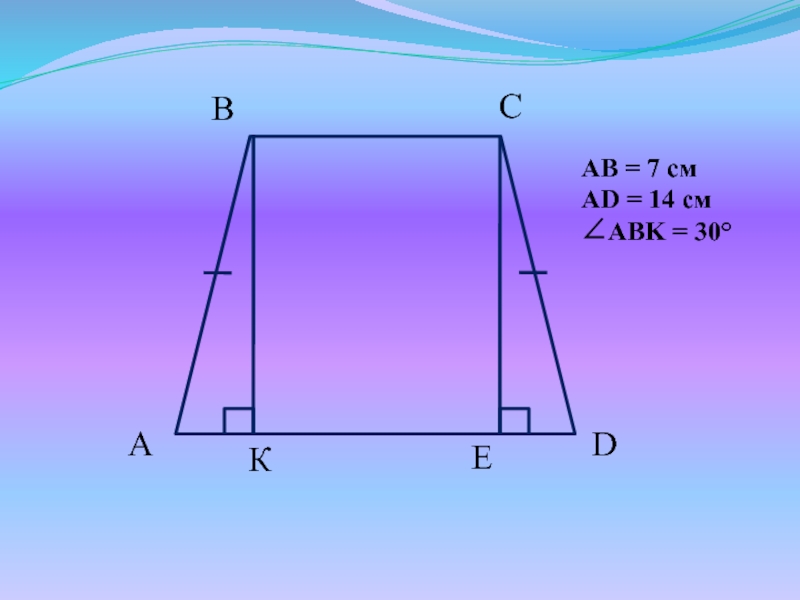
- 13. AB = 7 смAD = 14 смABK = 30
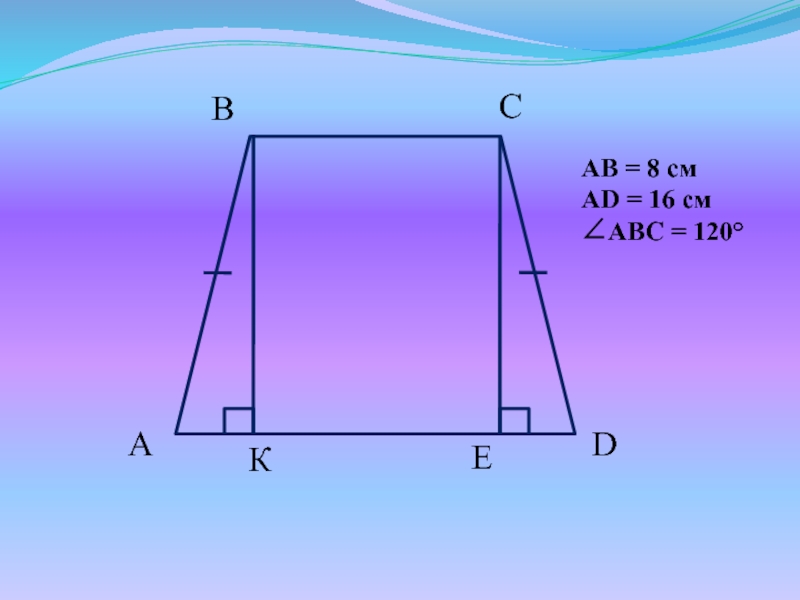
- 14. AB = 8 смAD = 16 смABC = 120
- 15. Задачи для самостоятельного решения
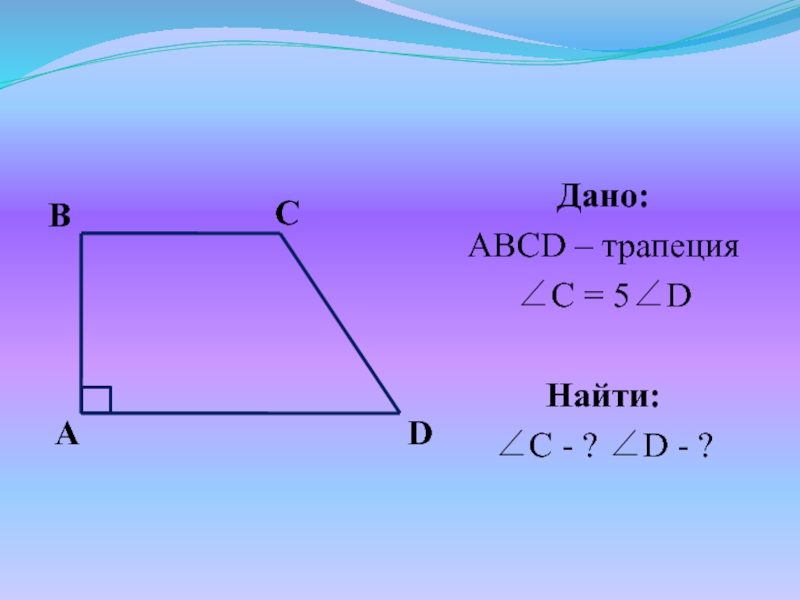
- 16. №1. В прямоугольной трапеции тупой угол больше острого в 5 раз. Найти углы трапеции.
- 17. Дано:ABCD – трапецияC = 5D Найти:C - ? D - ?DCAB
- 18. Решение:Т. к. ABCD – трапеция, то BC
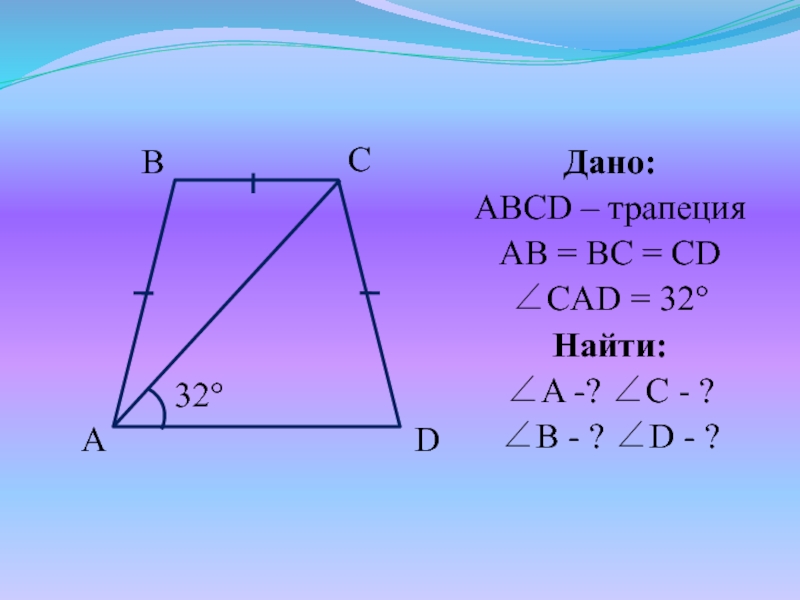
- 19. №2. Диагональ равнобедренной трапеции образует с основанием
- 20. Дано:ABCD – трапецияAB = BC = CDCAD
- 21. Решение:Т. к. ABCD – трапеция, то BC
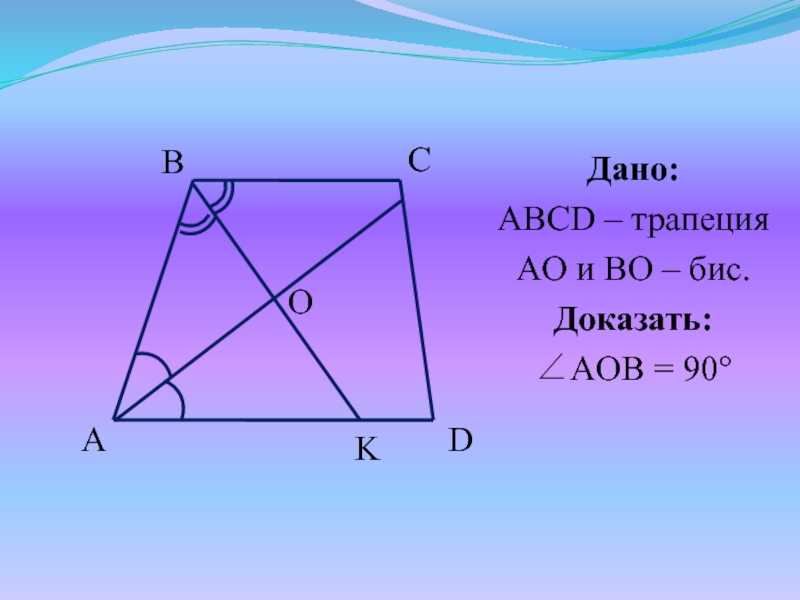
- 22. №3. O – точка пересечения биссектрис углов
- 23. Дано:ABCD – трапецияAO и BO – бис.Доказать:AOB = 90ABCDOK
- 24. Доказательство:BK – биссектриса, BK ∩ AD =
- 25. №4. Доказать, что высота равнобедренной трапеции, проведенная
- 26. Дано:ABCD – трапецияAB = CD BK
- 27. Доказательство:Проведем CE AD Рассмотрим ΔABK и
- 28. №5. В равнобедренной трапеции один из острых
- 29. Дано:ABCD –трапецияAB = CD = 16 смA = 60 Найти:BС - ? AD - ?16 см60
- 30. Решение:Проведем BK AD: ΔABK – прямоугольный
- 31. №6. В равнобедренной трапеции биссектриса, проведенная из
- 32. Дано:ABCD – трапецияAB = CD = 14
- 33. Решение:BK || CD (по условию)
Трапеция
Слайд 1Департамент образования города Москвы
Северо-Западное окружное управление образования
Презентация по геометрии на тему
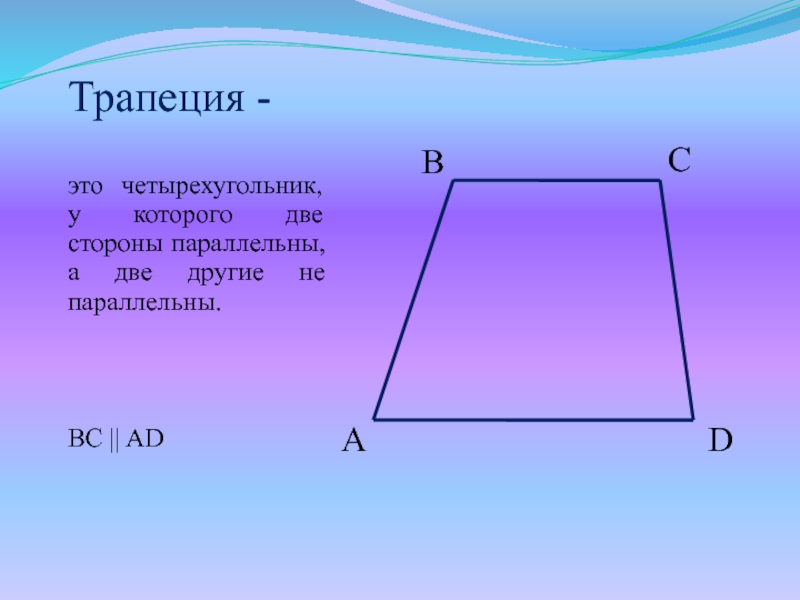
Слайд 3Трапеция -
это четырехугольник, у которого две стороны параллельны, а две
другие не параллельны.
BC || AD
BC || AD
A
B
C
D
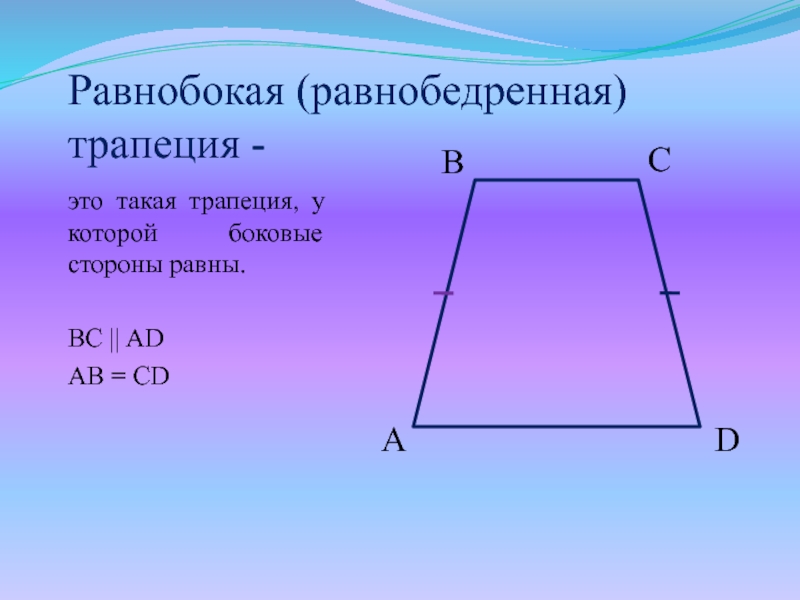
Слайд 8Равнобокая (равнобедренная) трапеция -
это такая трапеция, у которой боковые стороны
равны.
BC || AD
AB = CD
BC || AD
AB = CD
A
B
C
D
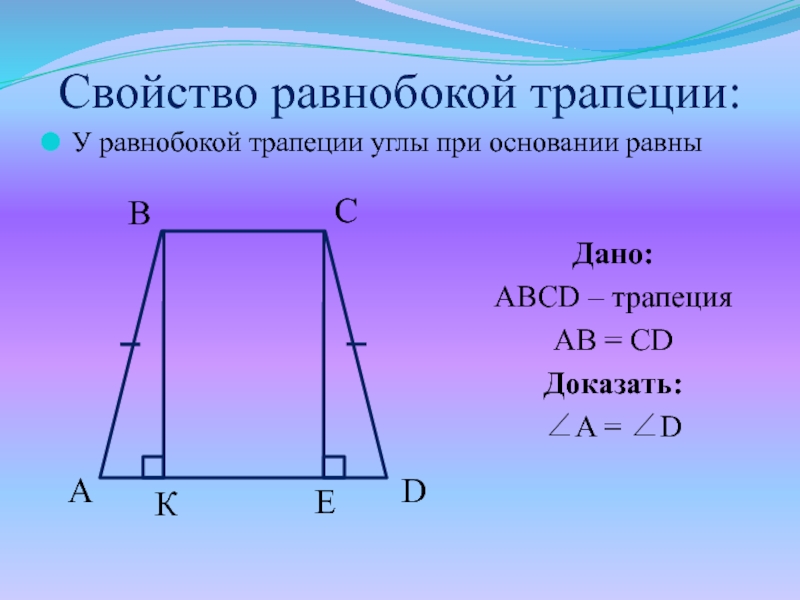
Слайд 9Свойство равнобокой трапеции:
У равнобокой трапеции углы при основании равны
A
B
C
D
К
Е
Дано:
ABCD – трапеция
AB
= CD
Доказать:
A = D
Доказать:
A = D
Слайд 10Доказательство:
Проведем BK AD и CE AD:
K = E =
90 => ΔABK и ΔCED – прямоугольные
2) Рассмотрим ΔABK и ΔCED:
AB = CD (по условию)
BC || AD ΔABK = ΔCED
BK AD => BK = CE (по гипотенузе и
CE AD => BK || CE катету)
3) Т.к. ΔABK = ΔCED , то A = D
ч.т.д.
2) Рассмотрим ΔABK и ΔCED:
AB = CD (по условию)
BC || AD ΔABK = ΔCED
BK AD => BK = CE (по гипотенузе и
CE AD => BK || CE катету)
3) Т.к. ΔABK = ΔCED , то A = D
ч.т.д.
Слайд 18Решение:
Т. к. ABCD – трапеция, то BC || AD C +
D = 180 (как внутренние односторонние)
Пусть C = x, тогда D = 5x x + 5x = 180 6x = 180 x = 30.
C = 30, D = 150
Ответ: 30, 150.
Пусть C = x, тогда D = 5x x + 5x = 180 6x = 180 x = 30.
C = 30, D = 150
Ответ: 30, 150.
Слайд 19№2. Диагональ равнобедренной трапеции образует с основанием угол в 32, а
ее боковая сторона равна меньшему основанию. Найти углы трапеции.
Слайд 21Решение:
Т. к. ABCD – трапеция, то BC || AD Зн. CAD
= ACB (как внутренние накрест лежащие)
Т. к. AB = BC (по условию), то ACB = BAC
A = BAC + CAD = 32 + 32 = 64 = D (ABCD – равнобокая трапеция)
A + B = 180 (BC || AD) B = 180 - A = 180 - 64 = 116 = C
Ответ: 64, 116.
Т. к. AB = BC (по условию), то ACB = BAC
A = BAC + CAD = 32 + 32 = 64 = D (ABCD – равнобокая трапеция)
A + B = 180 (BC || AD) B = 180 - A = 180 - 64 = 116 = C
Ответ: 64, 116.
Слайд 24Доказательство:
BK – биссектриса, BK ∩ AD = K
Т. к. ABCD
– трапеция, то BC || AD Рассмотрим секущую BK: CBK = AKB (как внутренние накрест лежащие) ABK = CBK (BK – биссектриса) Зн. ABK = AKB => ΔABK – равнобедренный
Т. к. AO – биссектриса в ΔABK, то AO – высота, т. е. AO BK.
BO BK, а зн. AO BO, т. е. AOB = 90
ч.т.д.
Т. к. AO – биссектриса в ΔABK, то AO – высота, т. е. AO BK.
BO BK, а зн. AO BO, т. е. AOB = 90
ч.т.д.
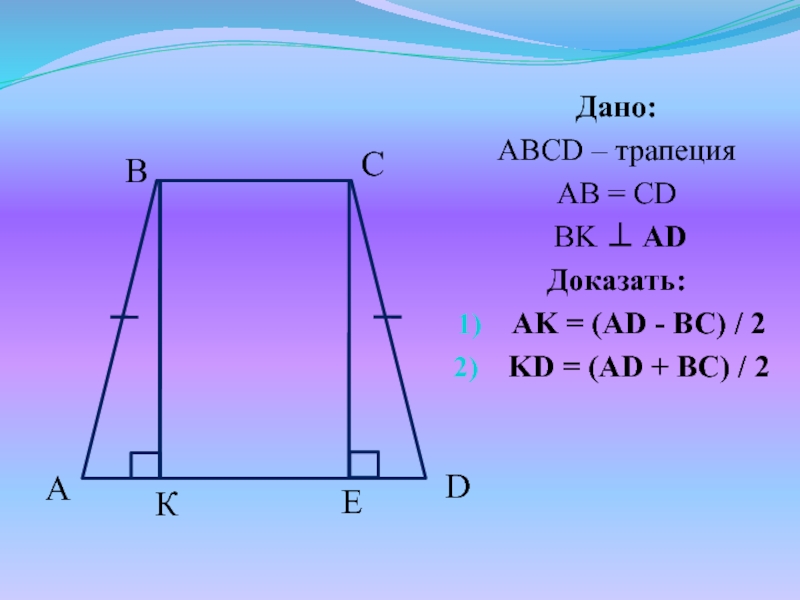
Слайд 25№4. Доказать, что высота равнобедренной трапеции, проведенная из вершины тупого угла,
делит большее основание на отрезки, один из которых равен полусумме ее оснований, а второй - полуразности.
Слайд 27Доказательство:
Проведем CE AD Рассмотрим ΔABK и ΔCED – прямоугольные: AB
= CD (ABCD – равнобедренная трапеция) BK = EC (как отрезки параллельных прямых, заключенные между параллельными прямыми) Зн. ΔABK = ΔCED (по гипотенузе и катету), т.е. AK = ED
AD = AK + KE + ED KE = BC (т.к. KBCE - прямоугольник) => AD = AK + BC + AK 2 AK = AD – BC AK = (AD - BC) / 2
KD = AD – AK = AD - (AD - BC) / 2 = (2 AD – AD + BC) / 2 KD = (AD - BC) / 2
ч.т.д.
AD = AK + KE + ED KE = BC (т.к. KBCE - прямоугольник) => AD = AK + BC + AK 2 AK = AD – BC AK = (AD - BC) / 2
KD = AD – AK = AD - (AD - BC) / 2 = (2 AD – AD + BC) / 2 KD = (AD - BC) / 2
ч.т.д.
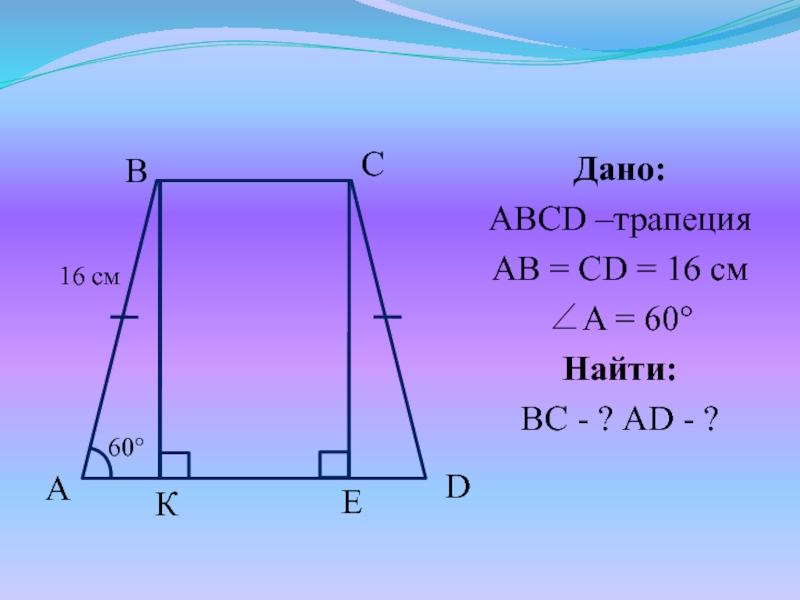
Слайд 28№5. В равнобедренной трапеции один из острых углов равен 60, а
длина боковой стороны равна 16 см. Найти основания трапеции, если их сумма равна 38 см.
Слайд 30Решение:
Проведем BK AD: ΔABK – прямоугольный A = 60, зн.
ABK = 30 AK = ½AB = 16 : 2 = 8 (см) (катет, лежащий против угла в 30)
KD = (AD + BC) / 2 = 38 : 2 = 19 (см)
AD = AK + KD = 8 + 19 = 27 (см)
BC = AD – 2 AK = 27 – 16 = 11 (см)
Ответ: 27 см и 11 см.
KD = (AD + BC) / 2 = 38 : 2 = 19 (см)
AD = AK + KD = 8 + 19 = 27 (см)
BC = AD – 2 AK = 27 – 16 = 11 (см)
Ответ: 27 см и 11 см.
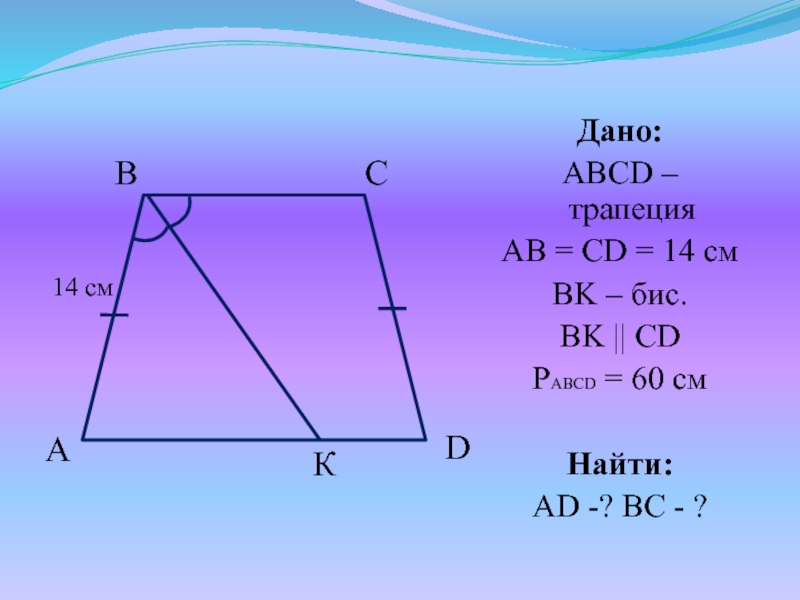
Слайд 31№6. В равнобедренной трапеции биссектриса, проведенная из вершины тупого угла, параллельна
боковой стороне. Вычислить основания трапеции, если ее периметр равен 60 см, а боковая сторона 14 см.
Слайд 33Решение:
BK || CD (по условию) KBCD
– пар-м BC || AD (ABCD – трапеция) (по признаку)
Т.к. BK – биссектриса, то ABK = KBC KBC = AKB (внутренние накрест лежащие при BC || AD и BK - секущей) => ABK = AKB, т.е. Δ ABK – равнобедренный AB = AK = 14 см
Пусть KD = x (см), тогда AD = x – 14 (см). PABCD = AB + BC + CD + AD = 60 (см) 14 + x + 14 + x + 14 = 60 42 + 2 x = 60 2 x = 18 x = 9 BC = KD = x = 9 (см), значит AD = x + 14 = 9 + 14 = 23 (см)
Ответ: 9 см и 23 см.
Т.к. BK – биссектриса, то ABK = KBC KBC = AKB (внутренние накрест лежащие при BC || AD и BK - секущей) => ABK = AKB, т.е. Δ ABK – равнобедренный AB = AK = 14 см
Пусть KD = x (см), тогда AD = x – 14 (см). PABCD = AB + BC + CD + AD = 60 (см) 14 + x + 14 + x + 14 = 60 42 + 2 x = 60 2 x = 18 x = 9 BC = KD = x = 9 (см), значит AD = x + 14 = 9 + 14 = 23 (см)
Ответ: 9 см и 23 см.