- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Точка, отрезок, прямая (7 класс)
Содержание
- 1. Презентация по геометрии на тему Точка, отрезок, прямая (7 класс)
- 2. Зарождение геометрииГеометрия возникла в результате практической деятельности
- 3. От практической геометрии к науке геометрияЗа несколько
- 4. Геометрия ЕвклидаПопытки греческих ученых привести геометрические факты
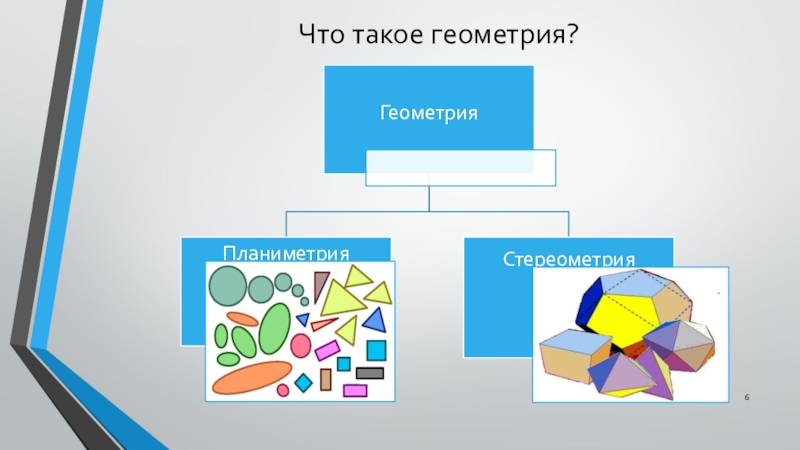
- 5. Что такое геометрия?Геометрия – это наука, занимающая
- 6. Что такое геометрия?
- 7. ТочкаТочка – это основная и самая простая
- 8. ПрямаяПрямая – это самая простая геометрическая фигура,
- 9. Способы обозначения прямойСтрочной латинской буквойПрямая а Двумя
- 10. Расположение прямой и точекКакова бы ни была
- 11. Расположение прямой и точекМожно ли через одну
- 12. Расположение прямой и точекСколько прямых можно провести
- 13. Расположение прямой и точекСколько точек пересечения могут
- 14. Вопросы:Могут ли прямые ОА и АВ быть
- 15. ОтрезокОтрезок – это часть прямой, которая ограничена
- 16. Самостоятельная работаНачертите прямую и обозначьте ее буквой
- 17. Домашнее заданиеПрочитать стр. 5-7«Провешивание прямой на местности»
- 18. Спасибо за внимание
Зарождение геометрииГеометрия возникла в результате практической деятельности людей: нужно было сооружать жилища, храмы, прокладывать дороги, оросительные каналы, устанавливать границы земельных участков и определять их размеры. В переводе с греческого слово «геометрия» означает «землемерие» («гео» — по-гречески
Слайд 2Зарождение геометрии
Геометрия возникла в результате практической деятельности людей: нужно было сооружать
жилища, храмы, прокладывать дороги, оросительные каналы, устанавливать границы земельных участков и определять их размеры.
В переводе с греческого слово «геометрия» означает «землемерие» («гео» — по-гречески земля, а «метрео» — мерить). Такое название объясняется тем, что зарождение геометрии было связано с различными измерительными работами.
Важную роль играли и эстетические потребности людей: желание украсить свои жилища и одежду, рисовать картины окружающей жизни. Все это способствовало формированию и накоплению геометрических сведений.
В переводе с греческого слово «геометрия» означает «землемерие» («гео» — по-гречески земля, а «метрео» — мерить). Такое название объясняется тем, что зарождение геометрии было связано с различными измерительными работами.
Важную роль играли и эстетические потребности людей: желание украсить свои жилища и одежду, рисовать картины окружающей жизни. Все это способствовало формированию и накоплению геометрических сведений.
Слайд 3От практической геометрии к науке геометрия
За несколько столетий до нашей эры
в Вавилоне, Китае, Египте и Греции уже существовали начальные геометрические знания, которые добывались в основном опытным путем, но они не были еще систематизированы и передавались от поколения к поколению в виде правил и рецептов, например, правил нахождения площадей фигур, объемов тел, построения прямых углов и т. д.
Не было еще доказательств этих правил, и их изложение не представляло собой научной теории.
Первым, кто начал получать геометрические факты при помощи рассуждений (доказательств), был древнегреческий математик Фалес (VI в. до н. э.), который в своих исследованиях применял перегибание чертежа, поворот части фигуры и так далее, то есть то, что на современном геометрическом языке называется движением.
Постепенно геометрия становится наукой, в которой большинство фактов устанавливается путем выводов, рассуждений, доказательств.
Не было еще доказательств этих правил, и их изложение не представляло собой научной теории.
Первым, кто начал получать геометрические факты при помощи рассуждений (доказательств), был древнегреческий математик Фалес (VI в. до н. э.), который в своих исследованиях применял перегибание чертежа, поворот части фигуры и так далее, то есть то, что на современном геометрическом языке называется движением.
Постепенно геометрия становится наукой, в которой большинство фактов устанавливается путем выводов, рассуждений, доказательств.
Слайд 4Геометрия Евклида
Попытки греческих ученых привести геометрические факты в систему начинаются уже
с V в. до н. э. Наибольшее влияние на всё последующее развитие геометрии оказали труды греческого ученого Евклида, жившего в Александрии в III в. до н. э. Сочинение Евклида «Начала» почти 2000 лет служило основной книгой, по которой изучали геометрию. В «Началах» были систематизированы известные к тому времени геометрические сведения, и геометрия впервые предстала как математическая наука.
Эта книга была переведена на языки многих народов мира, а сама геометрия, изложенная в ней, стала называться евклидовой геометрией.
Эта книга была переведена на языки многих народов мира, а сама геометрия, изложенная в ней, стала называться евклидовой геометрией.
Слайд 5Что такое геометрия?
Геометрия – это наука, занимающая изучение геометрических фигур и
их свойств.
В геометрии изучаются формы, размеры, взаимное расположение предметов независимо от их других свойств: массы, цвета и т. д. Отвлекаясь от этих свойств и беря во внимание только форму и размеры предметов, мы приходим к понятию геометрической фигуры.
В геометрии изучаются формы, размеры, взаимное расположение предметов независимо от их других свойств: массы, цвета и т. д. Отвлекаясь от этих свойств и беря во внимание только форму и размеры предметов, мы приходим к понятию геометрической фигуры.
Слайд 7Точка
Точка – это основная и самая простая геометрическая фигура. В переводе
с латинского языка слово точка – результат мгновенного касания, укол.
Точки обозначаются большими буквами латинского алфавита
Точки обозначаются большими буквами латинского алфавита
Слайд 8Прямая
Прямая – это самая простая геометрическая фигура, которая не имеет ни
начала, ни конца.
Слова «не имеет ни начала, ни конца» говорят о том, что прямая бесконечна.
Слова «не имеет ни начала, ни конца» говорят о том, что прямая бесконечна.
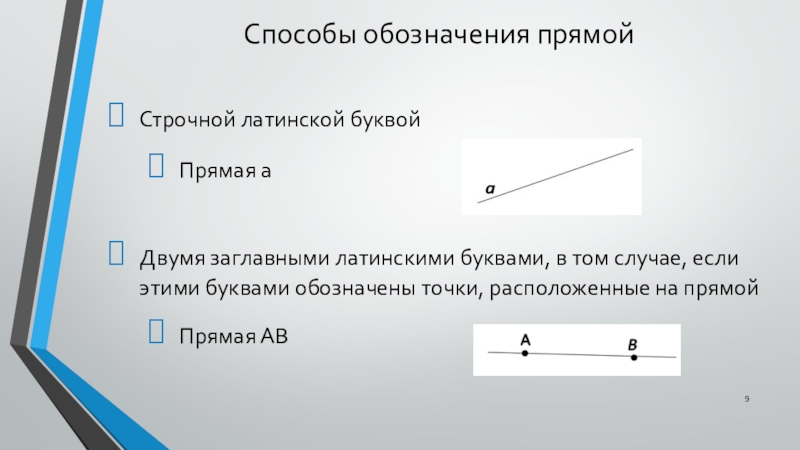
Слайд 9Способы обозначения прямой
Строчной латинской буквой
Прямая а
Двумя заглавными латинскими буквами, в
том случае, если этими буквами обозначены точки, расположенные на прямой
Прямая АВ
Прямая АВ
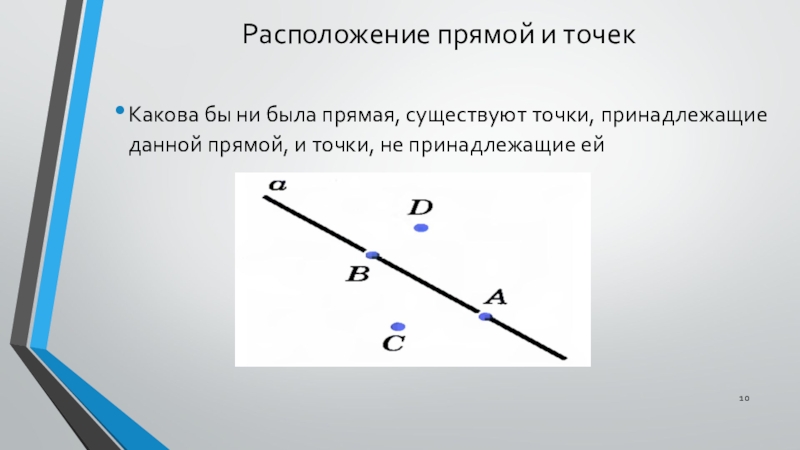
Слайд 10Расположение прямой и точек
Какова бы ни была прямая, существуют точки, принадлежащие
данной прямой, и точки, не принадлежащие ей
Слайд 11Расположение прямой и точек
Можно ли через одну точку провести прямую?
Сколько прямых
можно провести через одну точку?
Через одну точку можно провести бесконечное множество прямых.
Через одну точку можно провести бесконечное множество прямых.
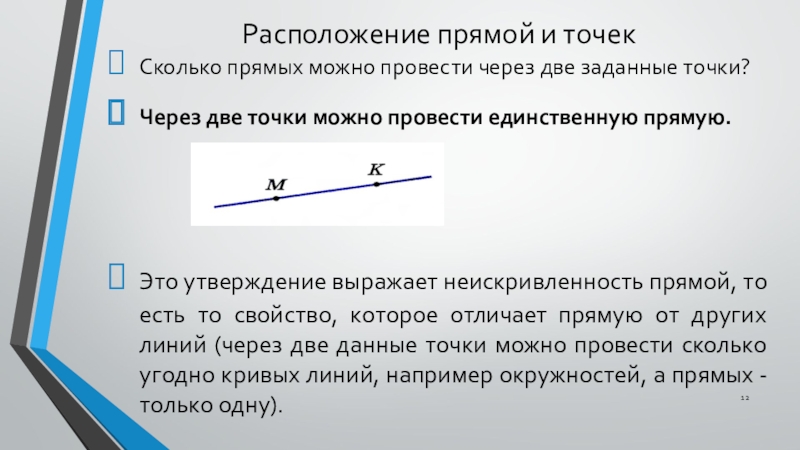
Слайд 12Расположение прямой и точек
Сколько прямых можно провести через две заданные точки?
Через
две точки можно провести единственную прямую.
Это утверждение выражает неискривленность прямой, то есть то свойство, которое отличает прямую от других линий (через две данные точки можно провести сколько угодно кривых линий, например окружностей, а прямых - только одну).
Это утверждение выражает неискривленность прямой, то есть то свойство, которое отличает прямую от других линий (через две данные точки можно провести сколько угодно кривых линий, например окружностей, а прямых - только одну).
Слайд 13Расположение прямой и точек
Сколько точек пересечения могут иметь две прямые?
Две прямые
могут пересекаться только в одной точке.
Прямые называются параллельными, если они лежат в одной плоскости и не пересекаются, сколько бы их не продолжали
Прямые называются параллельными, если они лежат в одной плоскости и не пересекаются, сколько бы их не продолжали
Слайд 14Вопросы:
Могут ли прямые ОА и АВ быть различными, если точка О
лежит на прямой АВ?
Ответ: прямые ОА и АВ не могут быть различными, так как обе они проходят через точки А и О, а через две точки проходит только одна прямая.
Даны две прямые а и в, пересекающиеся в точке С, и точка Д, отличная от точки С и лежащая на прямой а. Может ли точка Д лежать на прямой в?
Ответ: точка Д не может лежать на прямой в, так как две прямые не могут иметь двух общих точек.
Ответ: прямые ОА и АВ не могут быть различными, так как обе они проходят через точки А и О, а через две точки проходит только одна прямая.
Даны две прямые а и в, пересекающиеся в точке С, и точка Д, отличная от точки С и лежащая на прямой а. Может ли точка Д лежать на прямой в?
Ответ: точка Д не может лежать на прямой в, так как две прямые не могут иметь двух общих точек.
Слайд 15Отрезок
Отрезок – это часть прямой, которая ограничена двумя точками (концами отрезка).
У
отрезка есть и начало и конец.
Основное свойство отрезка – это его длина. Длина отрезка – это расстояние между концами отрезка.
Отрезок обозначается заглавными латинскими буквами.
Отрезок АВ
Основное свойство отрезка – это его длина. Длина отрезка – это расстояние между концами отрезка.
Отрезок обозначается заглавными латинскими буквами.
Отрезок АВ
Слайд 16Самостоятельная работа
Начертите прямую и обозначьте ее буквой в.
Отметьте точку М, лежащую
на прямой в.
Отметьте точку Д, не лежащую на прямой в.
Используя символы ∈ и ∉, запишите предложение: «Точка М лежит па прямой в, а точка Д не лежит на ней».
Начертите прямые а и в, пересекающиеся в точке К. На прямой а отметьте точку С, отличную от точки К.
Являются ли прямые КС и а различными прямыми? Ответ обоснуйте.
Может ли прямая в проходить через точку С? Ответ обоснуйте.
Отметьте точку Д, не лежащую на прямой в.
Используя символы ∈ и ∉, запишите предложение: «Точка М лежит па прямой в, а точка Д не лежит на ней».
Начертите прямые а и в, пересекающиеся в точке К. На прямой а отметьте точку С, отличную от точки К.
Являются ли прямые КС и а различными прямыми? Ответ обоснуйте.
Может ли прямая в проходить через точку С? Ответ обоснуйте.
Слайд 17Домашнее задание
Прочитать стр. 5-7
«Провешивание прямой на местности» можно законспектировать! (на след.
Уроке устный опрос)
Задачи № 4,6,7
Дополнительные задачи *:
Сколько точек пересечения могут иметь три прямые? Рассмотрите все возможные случаи и сделайте соответствующие рисунки.
На плоскости даны три точки. Сколько прямых можно провести через эти точки так, чтобы на каждой прямой лежали хотя бы две из данных точек? Рассмотрите все возможные случаи и сделайте рисунки.
Задачи № 4,6,7
Дополнительные задачи *:
Сколько точек пересечения могут иметь три прямые? Рассмотрите все возможные случаи и сделайте соответствующие рисунки.
На плоскости даны три точки. Сколько прямых можно провести через эти точки так, чтобы на каждой прямой лежали хотя бы две из данных точек? Рассмотрите все возможные случаи и сделайте рисунки.