- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Теорема Пифагора и способы её доказательства
Содержание
- 1. Презентация по геометрии на тему Теорема Пифагора и способы её доказательства
- 2. Теорема Пифагора – важнейшее утверждение
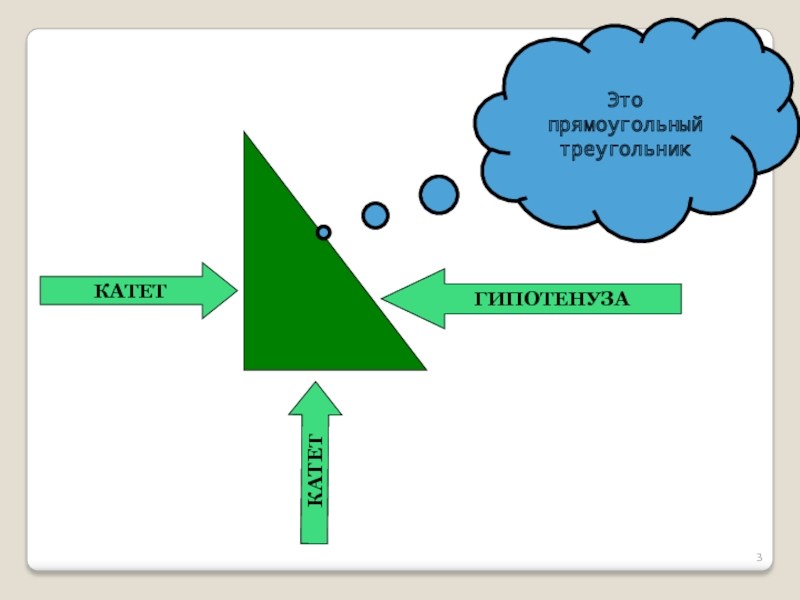
- 3. ГИПОТЕНУЗАКАТЕТКАТЕТЭто прямоугольный треугольник
- 4. На этом свойстве прямоугольного треугольника и основана
- 5. 1. Доказательства, основанные на использовании понятия равновеликости
- 6. Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах. Доказательство Пифагора
- 7. Квадрат, построенный на гипотенузе
- 8. 2. Аддитивные доказательства. Аддитивные доказательства - это
- 9. Доказательство Эпштейна Дано: ABC - прямоугольный треугольник с
- 10. 3. Доказательства методом построения Здесь вы найдете доказательства, для осуществления которых использовались дополнительные построения.
- 11. 1. Построим треугольник ABC с прямым углом
- 12. Что и требовалось доказать!6. Как мы видим,
- 13. 4. Алгебраический метод доказательстваЭти доказательства, основанные на
- 14. Доказательство Мёльманна1. Площадь данного треугольника с одной
- 15. Что и требовалось доказать!2. Имеем: 0,5ab=0,5pr=0,5(a+b+c)·0,5(a+b-c)0,5ab=0,5(a+b+c)·0,5(a+b-c)аb=0,5(а2 +
- 16. 5. Доказательства методом разложенияПростейшие доказательства теоремы, для
- 17. Доказательство ПеригаляДоказательство Перигаля очень легкое. Два квадрата,
- 18. 6. Доказательство методом
- 19. На рисунке к обычной пифагоровой фигуре приставлены
- 20. 7. Другие доказательства. Доказательство с помощью косинуса
Слайд 2
Теорема Пифагора – важнейшее утверждение геометрии. Даже те, кто
Слайд 4На этом свойстве прямоугольного треугольника и основана теорема Пифагора. Она показывает
Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим —
И таким простым путем
К результату мы придём.
Слайд 51. Доказательства, основанные на использовании понятия равновеликости фигур.
Здесь вы
Слайд 6Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на
Доказательство Пифагора
Слайд 7 Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на
Почтовая марка по случаю переименования острова Самос в остров Пифагорейон. На марке надпись: « т.Пифагора. Эллас. 350 драхи».
Слайд 82. Аддитивные доказательства.
Аддитивные доказательства - это доказательства, которые основаны на
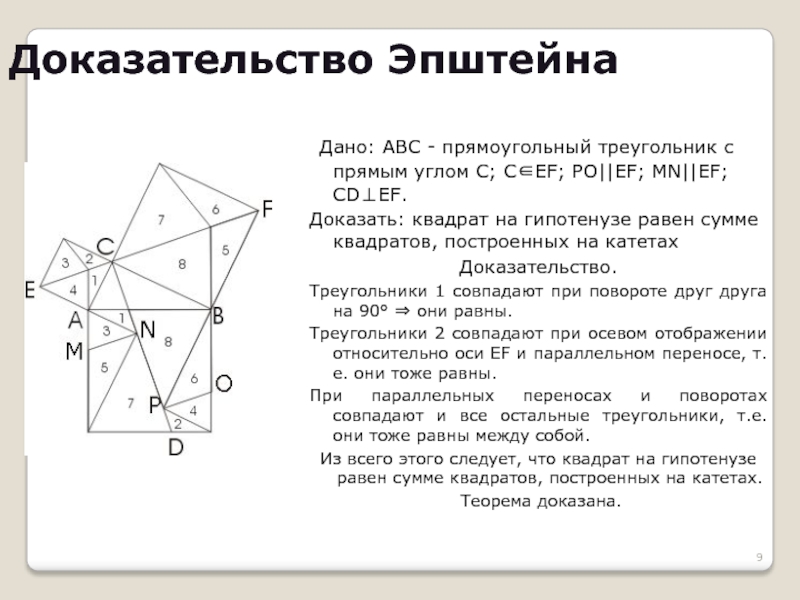
Слайд 9Доказательство Эпштейна
Дано: ABC - прямоугольный треугольник с прямым углом С; С∈EF;
Доказать: квадрат на гипотенузе равен сумме квадратов, построенных на катетах
Доказательство.
Треугольники 1 совпадают при повороте друг друга на 90° ⇒ они равны.
Треугольники 2 совпадают при осевом отображении относительно оси EF и параллельном переносе, т.е. они тоже равны.
При параллельных переносах и поворотах совпадают и все остальные треугольники, т.е. они тоже равны между собой.
Из всего этого следует, что квадрат на гипотенузе равен сумме квадратов, построенных на катетах.
Теорема доказана.
Слайд 103. Доказательства методом
построения
Здесь вы найдете доказательства, для
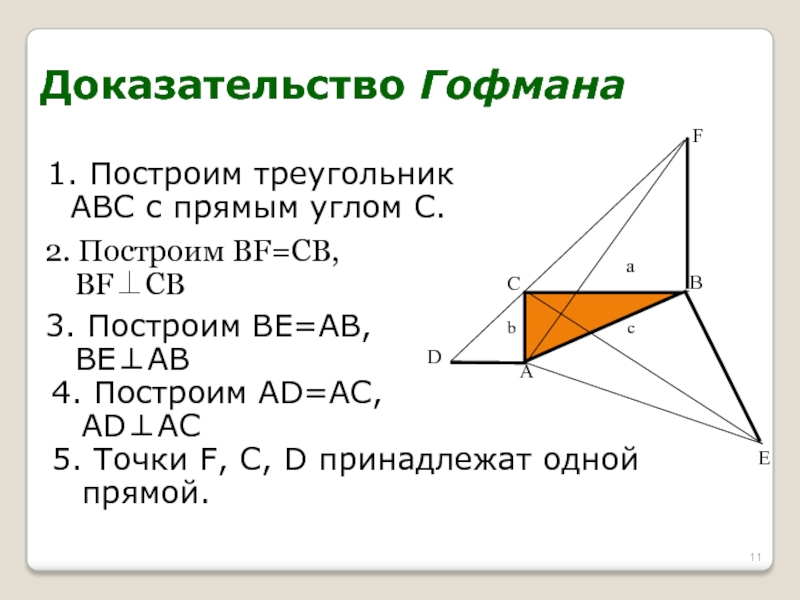
Слайд 111. Построим треугольник ABC с прямым углом С.
Доказательство Гофмана
2. Построим BF=CB,
3. Построим BE=AB, BEAB
4. Построим AD=AC, ADAC
5. Точки F, C, D принадлежат одной прямой.
Слайд 12Что и требовалось доказать!
6. Как мы видим, четырёхугольники ADFB и ACBE
7. Отнимем от обоих равновеликих четырёхугольников общий для них треугольник ABC, получим:
1/2а2+1/2b 2=1/2с 2
8. Соответственно:
а2+ b 2 =с 2
Доказательство Гофмана
a
Слайд 134. Алгебраический метод доказательства
Эти доказательства, основанные на применении в геометрии алгебраических
Слайд 14Доказательство Мёльманна
1. Площадь данного треугольника с одной стороны равна 0,5ab,
p – полупериметр треугольника,
r – радиус вписанной в него окружности (r=0,5(a+b-c)).
Слайд 15Что и требовалось доказать!
2. Имеем: 0,5ab=0,5pr=0,5(a+b+c)·0,5(a+b-c)
0,5ab=0,5(a+b+c)·0,5(a+b-c)
аb=0,5(а2 + ab – ac +
аb=0,5(а2 + b2- с2 +2ab)/·2
2аb=а2 + b2- с2 +2ab
а2 + b2- с2 =0
3. Отсюда следует, что с2= а2+b2
Доказательство Мёльманна
Слайд 165. Доказательства методом разложения
Простейшие доказательства теоремы, для понимания которых достаточно одного
Слайд 17Доказательство Перигаля
Доказательство Перигаля очень легкое. Два квадрата, построенные на катетах, расположены
Слайд 18
6. Доказательство методом вычитания
Наряду с доказательствами методом сложения можно
Слайд 19На рисунке к обычной пифагоровой фигуре приставлены сверху и снизу треугольники
Прямая DG обязательно пройдет через C. Заметим теперь, что шестиугольники DABGFE и CAJKHB равновелики. Если мы от первого из них отнимем треугольники 1 и 2, то останутся квадраты, построенные на катетах, а если от второго шестиугольника отнимем равные треугольники 1 и 3, то останется квадрат, построенный на гипотенузе. Отсюда вытекает, что квадрат, построенный на гипотенузе, равновелик сумме квадратов, построенных на катетах.
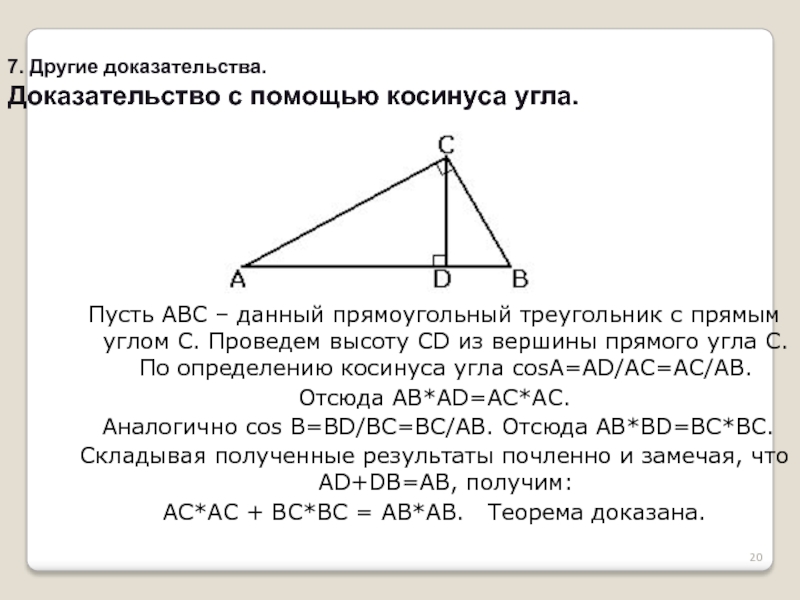
Слайд 207. Другие доказательства.
Доказательство с помощью косинуса угла.
Пусть АВС – данный прямоугольный
Отсюда АВ*AD=AC*АС.
Аналогично cos B=BD/BC=BC/AB. Отсюда АВ*BD=BC*BC.
Складывая полученные результаты почленно и замечая, что AD+DB=AB, получим:
AC*AC + BC*BC = AB*AB. Теорема доказана.