Презентация, доклад по геометрии на тему Теорема Менелая

Содержание

1. Презентация по геометрии на тему Теорема Менелая
2. Менелай Александрийский (I в) древнегреческий математик и астроном. Автор работ
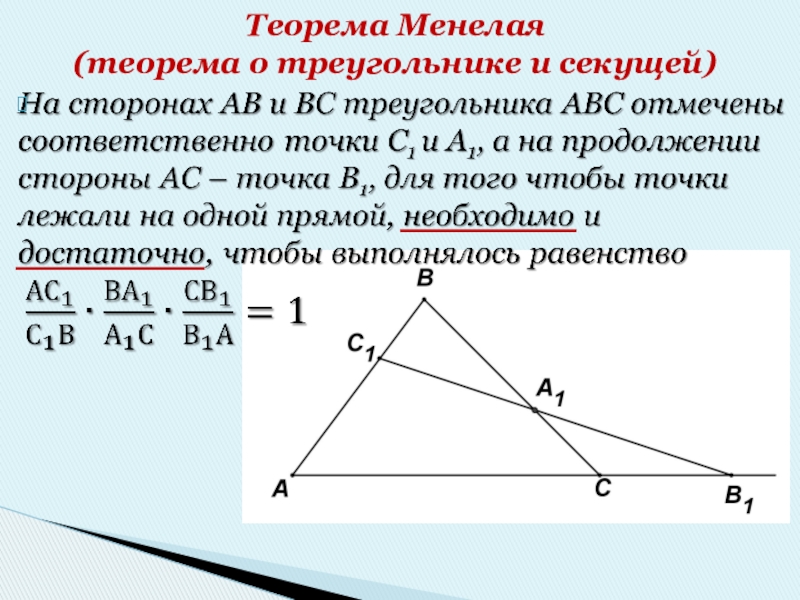
3. Теорема Менелая (теорема о треугольнике и секущей)
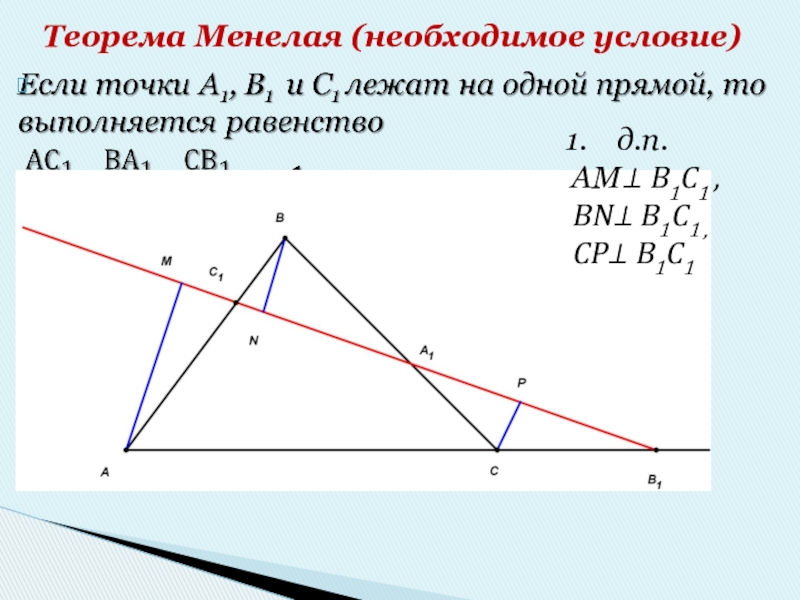
4. Теорема Менелая (необходимое условие)д.п. АМ⊥ В1С1 , BN⊥ В1С1 , CP⊥ В1С1
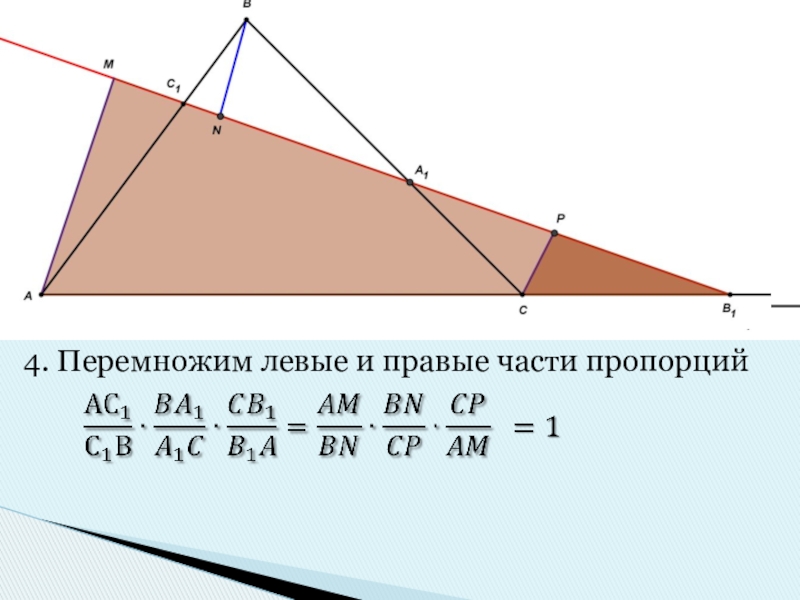
5. 4. Перемножим левые и правые части пропорций
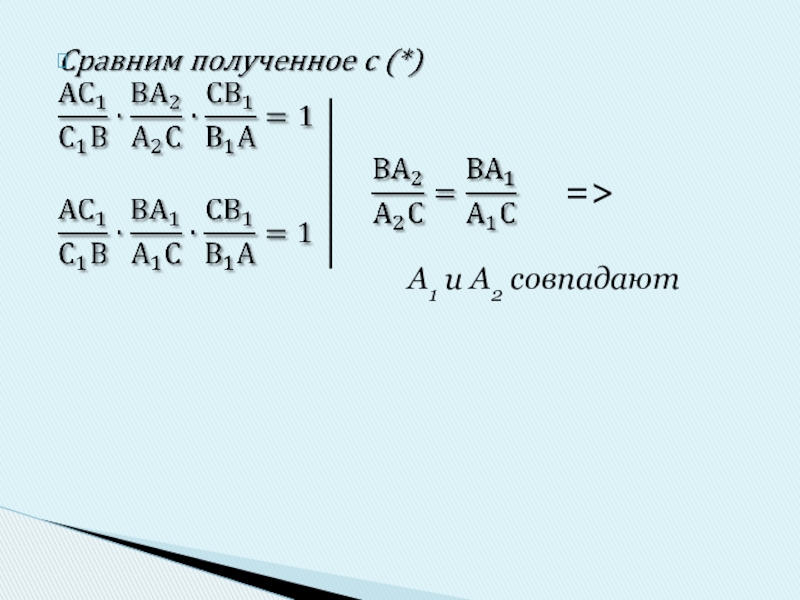
6. Теорема Менелая (достаточное условие)] C1B1 ⋂ BC = A2, тогда выполняется (*), только для A2
7. => A1 и A2 совпадают
8. В числитель заносится отрезок «от вершины до
9. ЗамечаниеТеорема справедлива и тогда, когда точки А1
10. 1. Записать теорему Менелая для треугольника АВР
11. 2. Точка N лежит на стороне AC
12. Задачи:
13. Задачи:
14. Задачи:5. В трапеции ABCD с основаниями AD
15. Задачи:6. Углы при одном из оснований трапеции

Менелай Александрийский (I в) древнегреческий математик и астроном. Автор работ по сферической тригонометрии: написал 6 книг о вычислении хорд и 3 книги “Сферики’’, сохранившиеся в арабском переводе. Для получения формул сферической тригонометрии использовал теорему, известную сегодня как теорема Менелая.

Главная
Геометрия
Презентация по геометрии на тему Теорема Менелая

Слайд 1Теорема Менелая
Решение задач

Слайд 2Менелай Александрийский (I в) древнегреческий математик и астроном. Автор работ по сферической тригонометрии: написал

6 книг о вычислении хорд и 3 книги “Сферики’’, сохранившиеся в арабском переводе. Для получения формул сферической тригонометрии использовал теорему, известную сегодня как теорема Менелая.

Менелай Александрийский (I в) древнегреческий математик и астроном. Автор работ по сферической тригонометрии: написал 6 книг о вычислении хорд и

Слайд 3Теорема Менелая (теорема о треугольнике и секущей)

Слайд 4Теорема Менелая (необходимое условие)
д.п.
АМ⊥ В1С1 ,
BN⊥ В1С1 ,
CP⊥

В1С1

Слайд 54. Перемножим левые и правые части пропорций

Слайд 6Теорема Менелая (достаточное условие)
] C1B1 ⋂ BC = A2, тогда
выполняется

(*), только для A2

Слайд 7=>
A1 и A2 совпадают

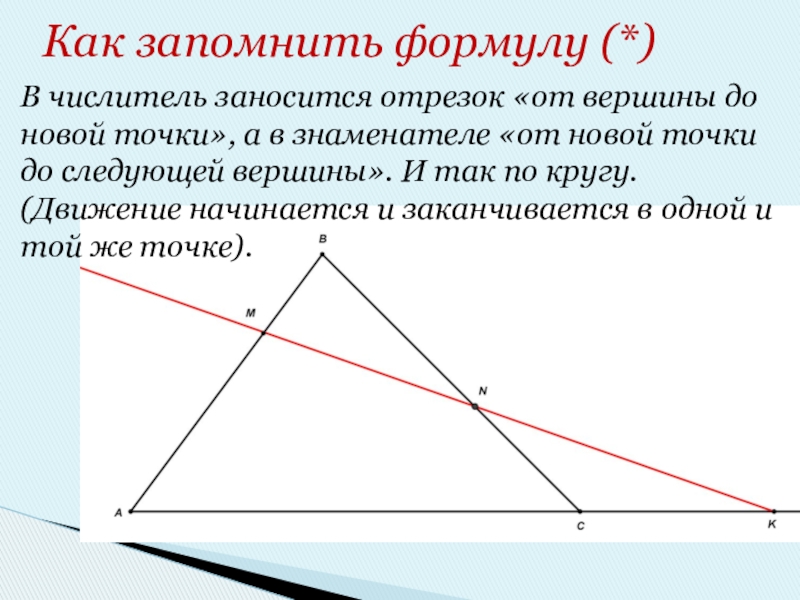
Слайд 8В числитель заносится отрезок «от вершины до новой точки», а в

знаменателе «от новой точки до следующей вершины». И так по кругу. (Движение начинается и заканчивается в одной и той же точке).

Как запомнить формулу (*)

В числитель заносится отрезок «от вершины до новой точки», а в знаменателе «от новой точки до следующей

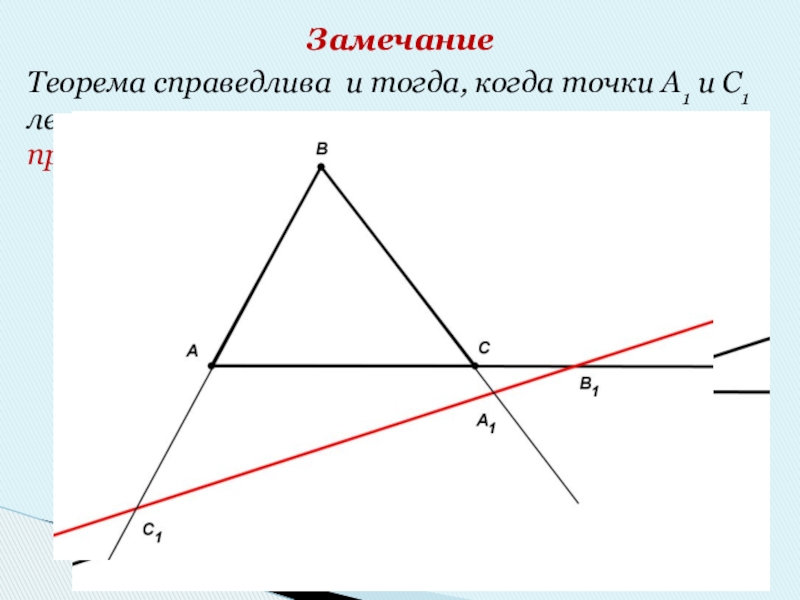
Слайд 9Замечание
Теорема справедлива и тогда, когда точки А1 и С1 лежат не

на сторонах треугольника, а на их продолжении.

ЗамечаниеТеорема справедлива и тогда, когда точки А1 и С1 лежат не на сторонах треугольника, а на их

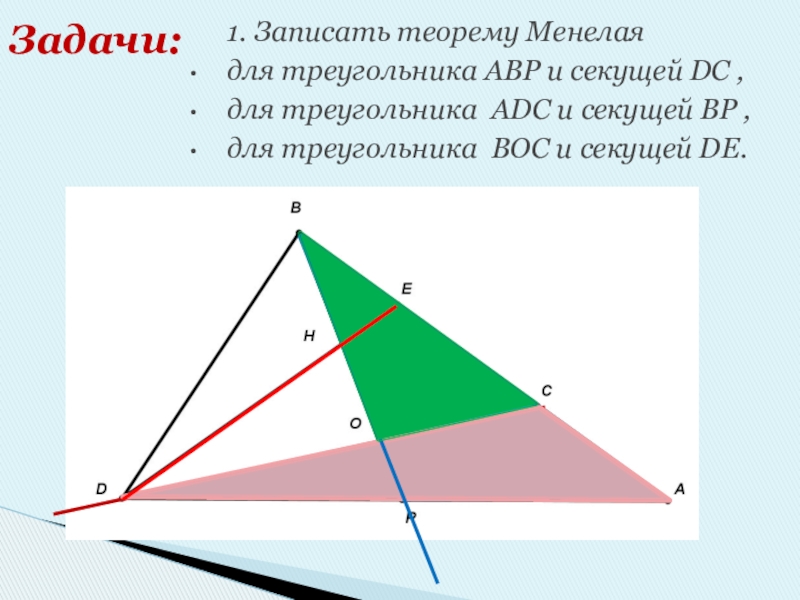
Слайд 10 1. Записать теорему Менелая
для треугольника АВР и секущей DC ,

для треугольника ADC и секущей BP ,
для треугольника BOC и секущей DE.

Задачи:

1. Записать теорему Менелая для треугольника АВР и секущей DC , для треугольника ADC и секущей BP

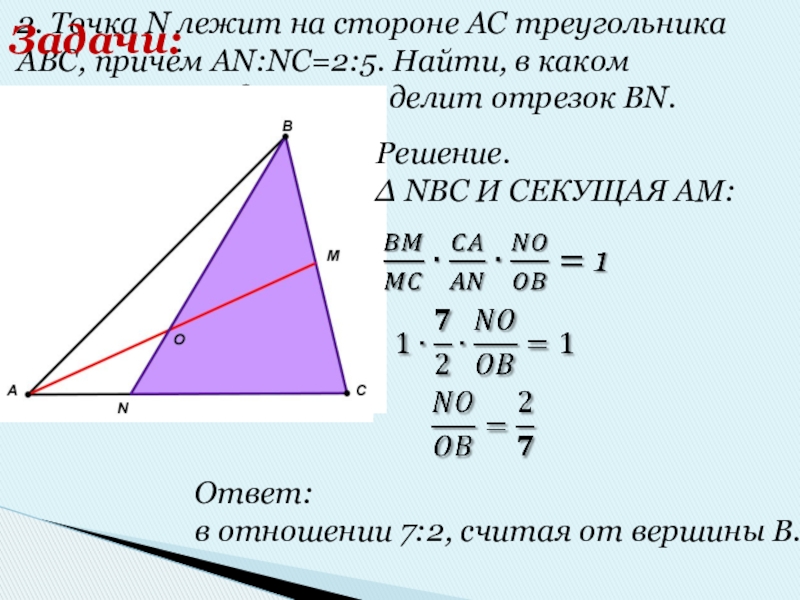
Слайд 112. Точка N лежит на стороне AC треугольника ABC, причём AN:NC=2:5.

Найти, в каком отношении медиана AM делит отрезок BN.

Решение.
Δ NBC И СЕКУЩАЯ АМ:

Ответ:
в отношении 7:2, считая от вершины В.

Задачи:

2. Точка N лежит на стороне AC треугольника ABC, причём AN:NC=2:5. Найти, в каком отношении медиана AM

Слайд 12Задачи:

Слайд 13Задачи:

Слайд 14Задачи:
5. В трапеции ABCD с основаниями AD и BC через точку

A проведена прямая, которая пересекает диагональ BD в точке P и боковую сторону CD в точке N, причём BP : PD = 2 : 3, CN : ND = 2 : 5. Найдите отношение длин оснований трапеции.

Задачи:5. В трапеции ABCD с основаниями AD и BC через точку A проведена прямая, которая пересекает диагональ

Слайд 15Задачи:
6. Углы при одном из оснований трапеции равны 39° и 51°,

а отрезки, соединяющие середины противоположных сторон трапеции, равны 19 и 17. Найдите основания трапеции.

Задачи:6. Углы при одном из оснований трапеции равны 39° и 51°, а отрезки, соединяющие середины противоположных сторон

Скачать презентацию

Презентация, доклад по геометрии на тему Теорема Менелая

Содержание

Слайд 1Теорема Менелая
Решение задач

Слайд 2Менелай Александрийский (I в) древнегреческий математик и астроном. Автор работ по сферической тригонометрии: написал

Слайд 3Теорема Менелая (теорема о треугольнике и секущей)

Слайд 4Теорема Менелая (необходимое условие)
д.п.
АМ⊥ В1С1 ,
BN⊥ В1С1 ,
CP⊥

Слайд 54. Перемножим левые и правые части пропорций

Слайд 6Теорема Менелая (достаточное условие)
] C1B1 ⋂ BC = A2, тогда
выполняется

Слайд 7=>
A1 и A2 совпадают

Слайд 8В числитель заносится отрезок «от вершины до новой точки», а в

Слайд 9Замечание
Теорема справедлива и тогда, когда точки А1 и С1 лежат не

Слайд 10 1. Записать теорему Менелая
для треугольника АВР и секущей DC ,

Слайд 112. Точка N лежит на стороне AC треугольника ABC, причём AN:NC=2:5.

Слайд 12Задачи:

Слайд 13Задачи:

Слайд 14Задачи:
5. В трапеции ABCD с основаниями AD и BC через точку

Слайд 15Задачи:
6. Углы при одном из оснований трапеции равны 39° и 51°,

Что такое shareslide.ru?

Обратная связь

Презентация, доклад по геометрии на тему Теорема Менелая

Содержание

Слайд 1Теорема МенелаяРешение задач

Слайд 2Менелай Александрийский (I в) древнегреческий математик и астроном. Автор работ по сферической тригонометрии: написал

Слайд 3Теорема Менелая (теорема о треугольнике и секущей)

Слайд 4Теорема Менелая (необходимое условие)д.п. АМ⊥ В1С1 , BN⊥ В1С1 , CP⊥

Слайд 54. Перемножим левые и правые части пропорций

Слайд 6Теорема Менелая (достаточное условие)] C1B1 ⋂ BC = A2, тогда выполняется

Слайд 7=> A1 и A2 совпадают

Слайд 8В числитель заносится отрезок «от вершины до новой точки», а в

Слайд 9ЗамечаниеТеорема справедлива и тогда, когда точки А1 и С1 лежат не

Слайд 10 1. Записать теорему Менелая для треугольника АВР и секущей DC ,

Слайд 112. Точка N лежит на стороне AC треугольника ABC, причём AN:NC=2:5.

Слайд 12Задачи:

Слайд 13Задачи:

Слайд 14Задачи:5. В трапеции ABCD с основаниями AD и BC через точку

Слайд 15Задачи:6. Углы при одном из оснований трапеции равны 39° и 51°,

Похожие презентации

Что такое shareslide.ru?

Обратная связь

Слайд 1Теорема Менелая
Решение задач

Слайд 4Теорема Менелая (необходимое условие)
д.п.
АМ⊥ В1С1 ,
BN⊥ В1С1 ,
CP⊥

Слайд 6Теорема Менелая (достаточное условие)
] C1B1 ⋂ BC = A2, тогда
выполняется

Слайд 7=>
A1 и A2 совпадают

Слайд 9Замечание
Теорема справедлива и тогда, когда точки А1 и С1 лежат не

Слайд 10 1. Записать теорему Менелая
для треугольника АВР и секущей DC ,

Слайд 14Задачи:
5. В трапеции ABCD с основаниями AD и BC через точку

Слайд 15Задачи:
6. Углы при одном из оснований трапеции равны 39° и 51°,