Тюгаева Дарья Денисовна
Руководитель: учитель математики Беляева Любовь Петровна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Теорема Пифагора
Содержание
- 1. Презентация по геометрии на тему Теорема Пифагора
- 2. Родился в 576 году до нашей эры.Прожил
- 3. - Делай то, что в
- 4. Всё есть число
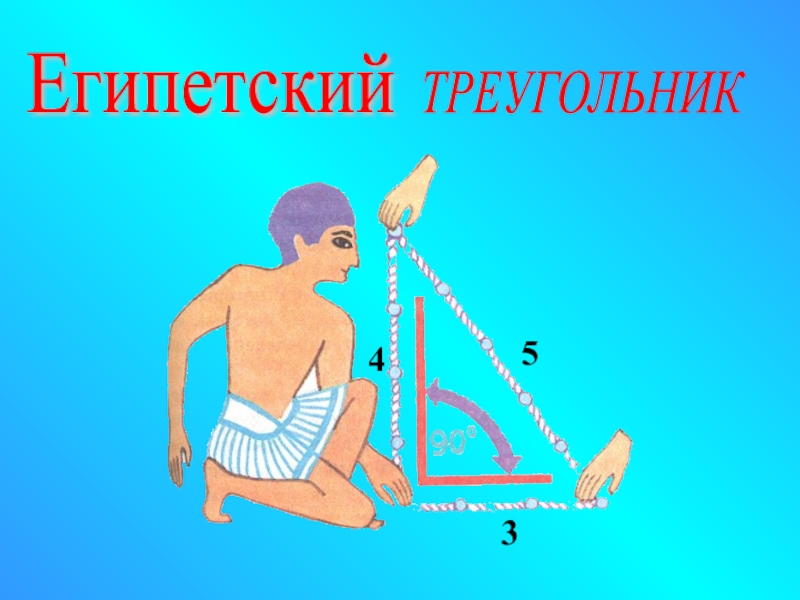
- 5. ТРЕУГОЛЬНИК Египетский 43, 4, 53, 4, 5 3 5
- 6. Простейшее доказательствоПростейшее доказательство теоремы получается в простейшем
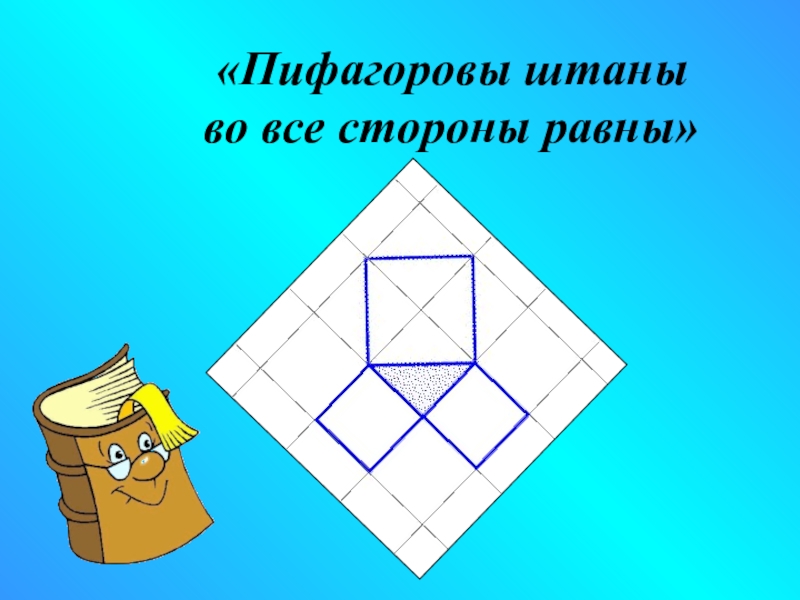
- 7. «Пифагоровы штаны во все стороны равны»
- 8. Теореме Пифагора Если дан нам треугольник И
- 9. «Теорема бабочки»
- 10. Древнеиндийская задачаНад озером тихимС полфута размеромВысился лотоса
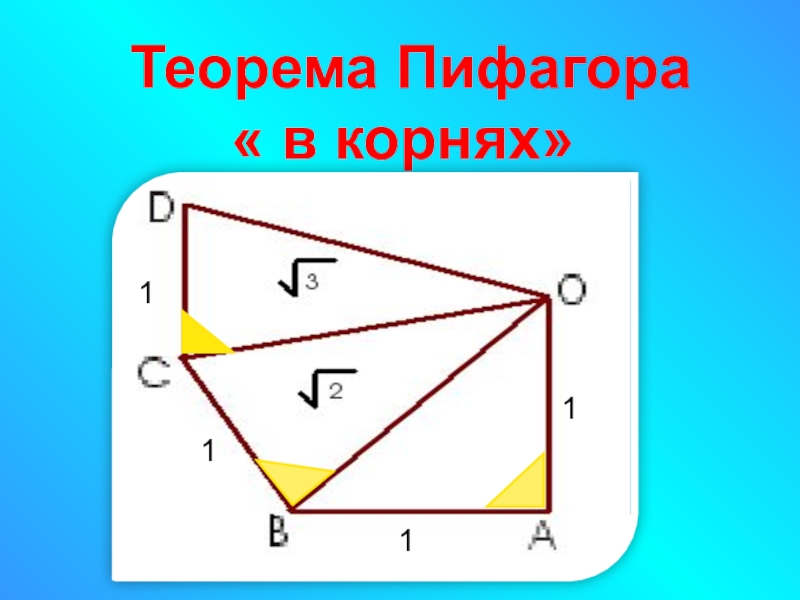
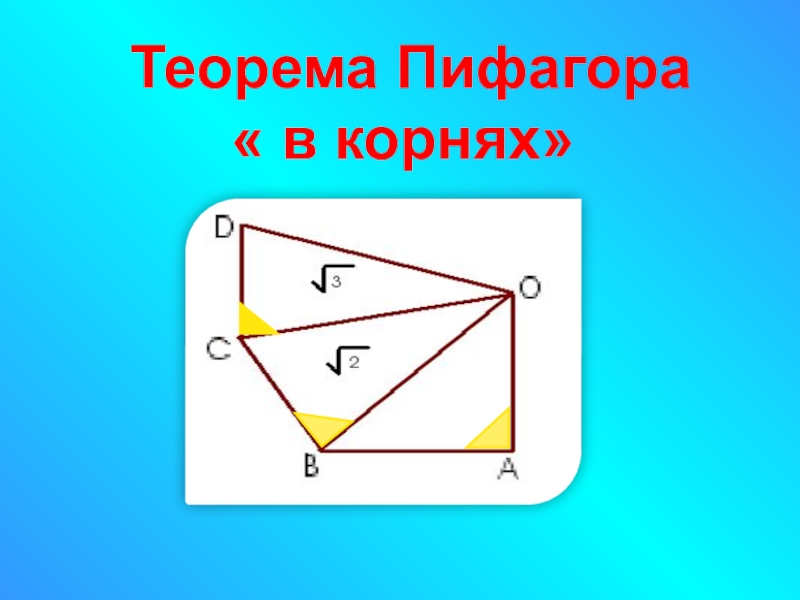
- 11. Теорема Пифагора « в корнях»
- 12. Теорема Пифагора «в углу»
- 13. Теорема Пифагора «в шкафу»
- 14. Какую наибольшую высоту должна иметь антенна АВ
- 15. «Гимн пифагорейцев восходящему солнцу» Ф.А. Бронников (1827-1902)
- 16. В 430—420-х гг. до н. э. (т.
- 17. Передать обитателям Марса сигнал в виде теоремы Пифагора. Удивительный факт
- 18. Причина популярности теоремы Пифагора триедина: это простота — красота — значимость.
- 19. Информационные источники.1.Атанасян Л.С. и др. Геометрия, 10
- 20. Теорема Пифагора « в корнях»
- 21. Какую наибольшую высоту должна иметь антенна АВ
Родился в 576 году до нашей эры.Прожил 80 лет.Умер в 496 году до нашей эры.о. Самос Пифагор
Слайд 3 - Делай то, что в последствии
не огорчит тебя и не принудит раскаиваться.
Пифагор - «убеждающий речью»
- Не пренебрегай здоровьем своего тела. Доставляй ему вовремя пищу и питьё, и упражнения, в которых оно нуждается.
- Не делай никогда того, что не знаешь,
но научись всему, что следует знать,
и тогда ты
будешь вести спокойную жизнь.
Заповеди пифагорейцев
Слайд 6Простейшее доказательство
Простейшее доказательство теоремы получается в простейшем случае равнобедренного прямоугольного треугольника.
В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников , чтобы убедиться в справедливости теоремы. Например, для треугольника ABC : квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах,- по два.
Теорема доказана.
Теорема доказана.
Теорема- рекордсменка
. В книге, опубликованной в 1940 году,
содержится 370 различных способов доказательств
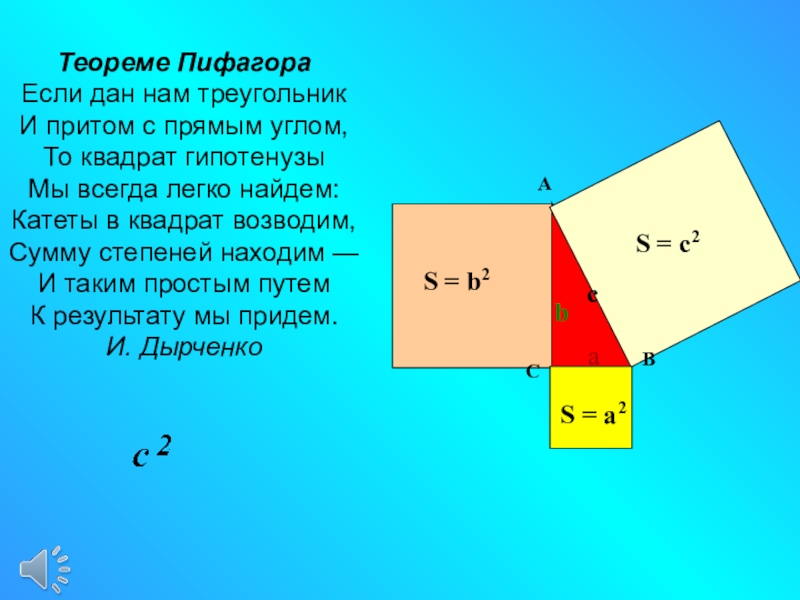
Слайд 8Теореме Пифагора Если дан нам треугольник И притом с прямым углом, То квадрат гипотенузы Мы
всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим —
И таким простым путем
К результату мы придем.
И. Дырченко
И. Дырченко
А
В
С
с
b
a
Слайд 10 Древнеиндийская задача
Над озером тихим
С полфута размером
Высился лотоса цвет.
Он рос одиноко,
И ветер
порывом
Отнёс его в сторону.Нет
Боле цветка над водой.
Нашёл же рыбак его
Ранней весною
В двух футах от места, где рос.
Итак, предложу я вопрос:
“Как озера вода здесь глубока?”
Отнёс его в сторону.Нет
Боле цветка над водой.
Нашёл же рыбак его
Ранней весною
В двух футах от места, где рос.
Итак, предложу я вопрос:
“Как озера вода здесь глубока?”
Слайд 14Какую наибольшую высоту должна иметь
антенна АВ мобильного оператора, чтобы передачу
можно было принимать в радиусе R=200 км? (радиус Земли r = 6380 км.)
Решение: Пусть AB= x,
BC=R=200 км, OC= =6380 км.
OB=OA+AB, OB=r + x.
Используя теорему Пифагора для треугольника ОСВ, получим Ответ: 2,3 км.
Теорема Пифагора
«на связи»
Слайд 16В 430—420-х гг. до н. э. (т. е. менее чем через
100 лет после смерти Пифагора) произошло невиданное событие: в Абдерах были выпущены монеты с изображением Пифагора .
Слайд 19Информационные источники.
1.Атанасян Л.С. и др. Геометрия, 10 – 11 кл. –
М.: Просвещение, 1992.
2.Волошин А.В. Пифагор. – М.: Просвещение, 1993.
3.Газета «Математика», № 21, 2006.
4.Газета «Математика», № 28, 1995.
5.Геометрия: Учеб.для 7 – 9 кл. общеобразоват. Учреждений/ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 6-е изд. – М.: Просвещение, 1996.
6.Глейзер Г.И. История математики в школе: IX – Xкл. Пособие для учителей. – М.: Просвещение, 1983.
7.Свешникова А. Путешествие в историю математики. – М., 1995.
8.Семёнов Е.Е. Изучаем геометрию: Кн. Для учащихся 6 – 8 кл. сред.шк. – М.: Просвещение, 1987.
9.Энциклопедический словарь юного математика. Сост. А.П. Савин. – М.: Педагогика, 1985.
10.www.narod.ru
11.www.ortoys.ru
12. http://www.mathsun.ru/pifagor.html
2.Волошин А.В. Пифагор. – М.: Просвещение, 1993.
3.Газета «Математика», № 21, 2006.
4.Газета «Математика», № 28, 1995.
5.Геометрия: Учеб.для 7 – 9 кл. общеобразоват. Учреждений/ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 6-е изд. – М.: Просвещение, 1996.
6.Глейзер Г.И. История математики в школе: IX – Xкл. Пособие для учителей. – М.: Просвещение, 1983.
7.Свешникова А. Путешествие в историю математики. – М., 1995.
8.Семёнов Е.Е. Изучаем геометрию: Кн. Для учащихся 6 – 8 кл. сред.шк. – М.: Просвещение, 1987.
9.Энциклопедический словарь юного математика. Сост. А.П. Савин. – М.: Педагогика, 1985.
10.www.narod.ru
11.www.ortoys.ru
12. http://www.mathsun.ru/pifagor.html
Слайд 21Какую наибольшую высоту должна иметь
антенна АВ мобильного оператора, чтобы передачу
можно было принимать в радиусе R=200 км? (радиус Земли r = 6380 км.)
Решение: Пусть AB= x,
BC=R=200 км, OC= =6380 км.
OB=OA+AB, OB=r + x.
Используя теорему Пифагора для треугольника ОСВ, получим Ответ: 2,3 км.
Теорема Пифагора
«на связи»
