- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Теорема Пифагора
Содержание
- 1. Презентация по геометрии на тему Теорема Пифагора
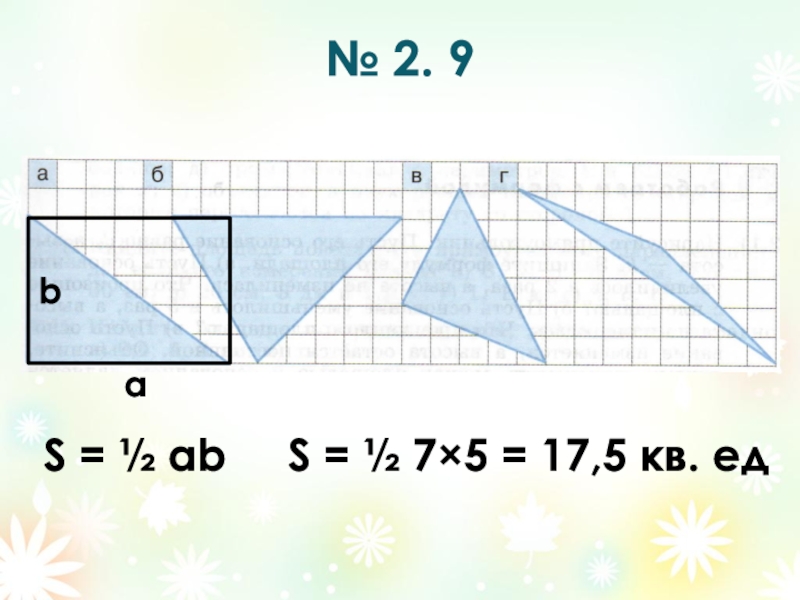
- 2. № 2. 9аbS = ½ аbS = ½ 7×5 = 17,5 кв. ед
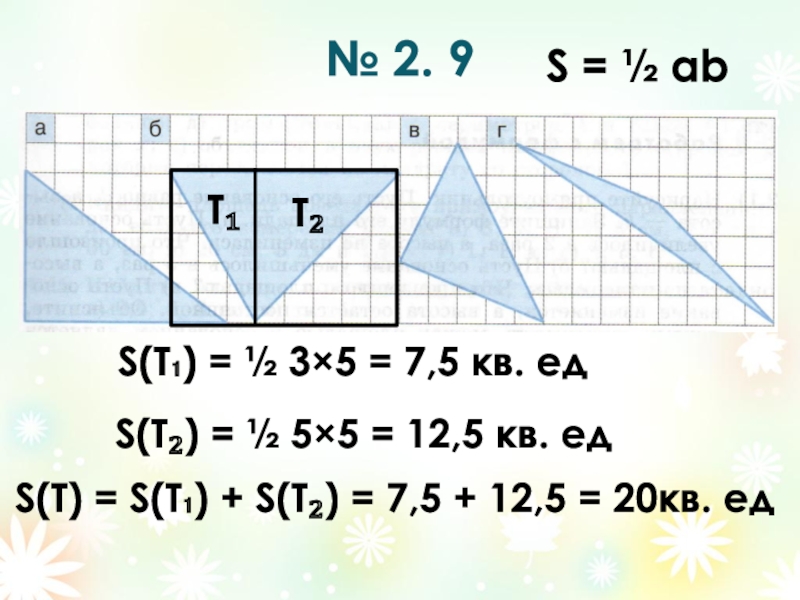
- 3. № 2. 9T₁T₂S = ½ аbS(T₁) =
- 4. № 2. 9
- 5. № 2. 9
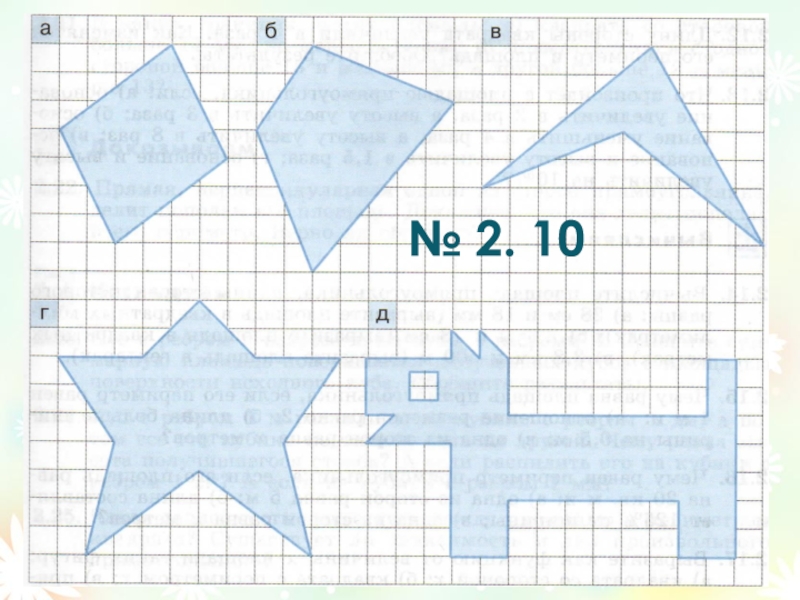
- 6. № 2. 10
- 7. Как называются стороны АС и ВС?Как называется
- 8. Вспомним свойства ПУТСумма острых углов
- 9. Определение прямоугольного треугольника.Название сторон прямоугольного треугольника.Как найти площадь прямоугольного треугольника по катетам.Свойства прямоугольного треугольника по
- 10. Прочитайте анаграмму: Tмаееро ПааиоргфTеорема Пифагора
- 11. Определение прямоугольного треугольника.Название сторон прямоугольного треугольника.Как найти
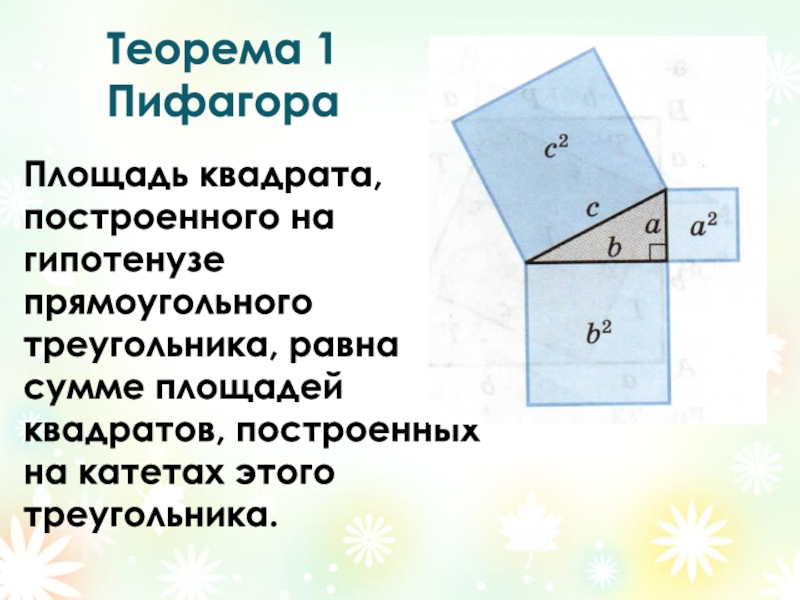
- 12. Теорема 1 Пифагора Площадь квадрата, построенного на
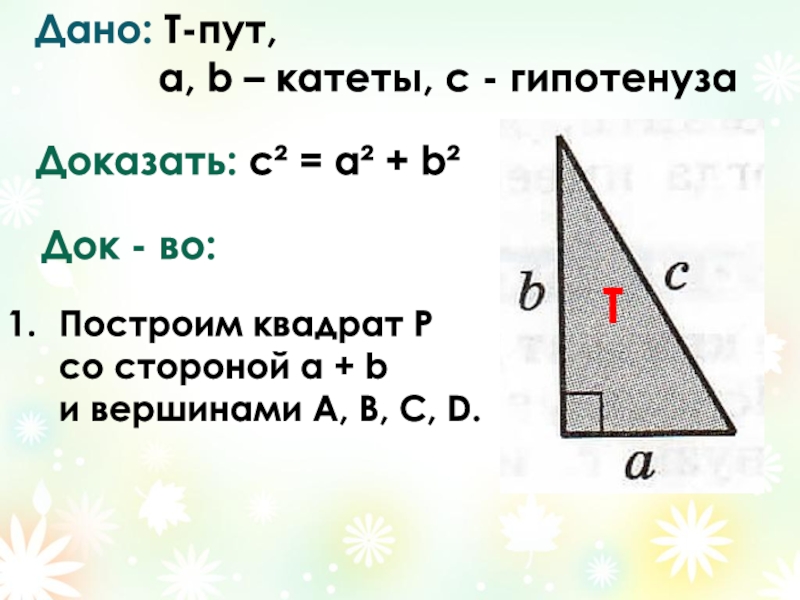
- 13. Дано: T-пут,
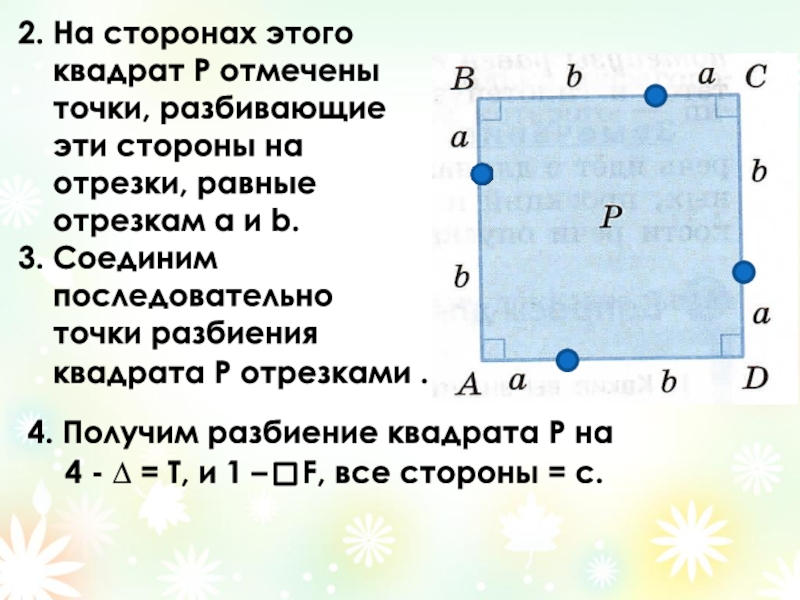
- 14. 2. На сторонах этого квадрат
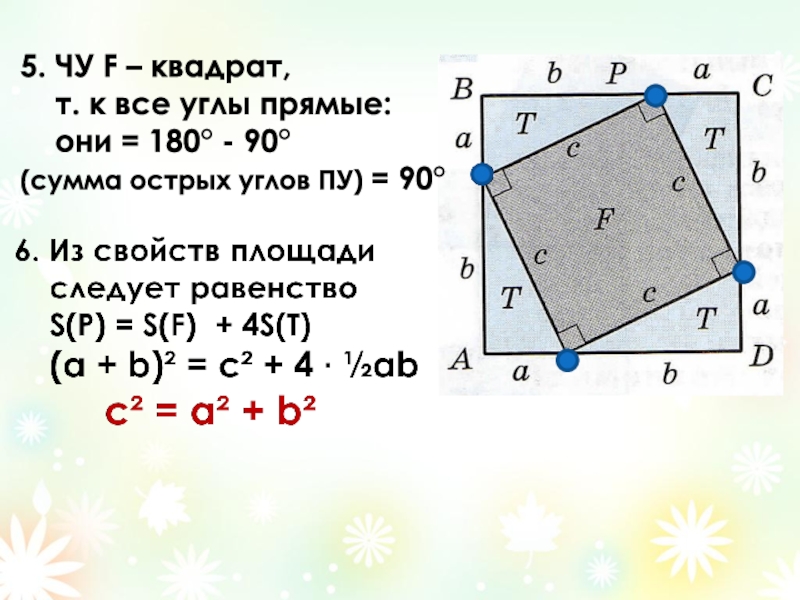
- 15. 5. ЧУ F – квадрат,
- 16. Построим квадрат Q со стороной
- 17. 5. Каждый из этих прямоугольников
- 18. Теорема 2 Пифагора В прямоугольном треугольнике квадрат
- 19. Дополняем теориюТеорема Пифагора – свойство прямоугольного треугольника.Обратная теорема Пифагора – признак прямоугольного треугольника.
- 20. № 3.1Если в треугольнике квадрат одной из
- 21. Дано: ∆АВС,
- 22. № 3.2(3, 4, 5), (6, 8, 10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (16, 30, 34), (21, 28, 35), (12, 35, 37), (15, 36, 39), (24, 32, 40), (9, 40, 41), (14, 48, 50), (30, 40, 50)
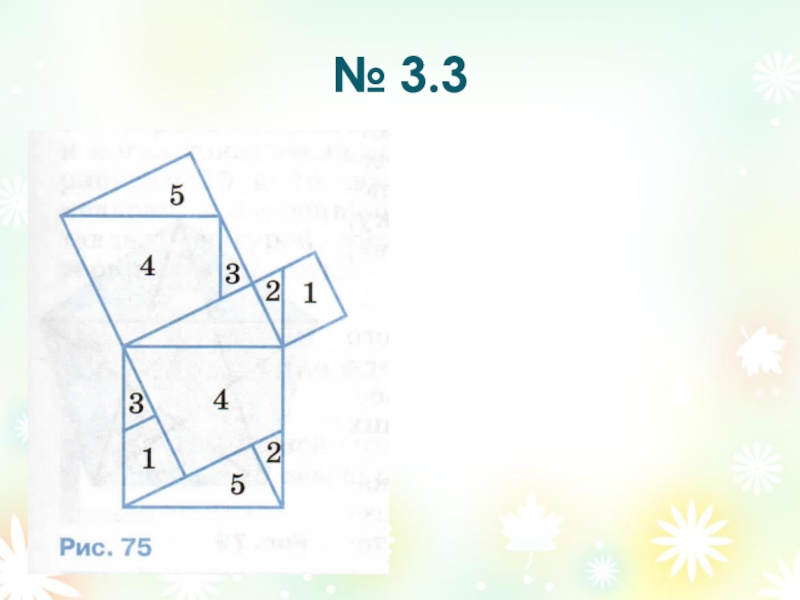
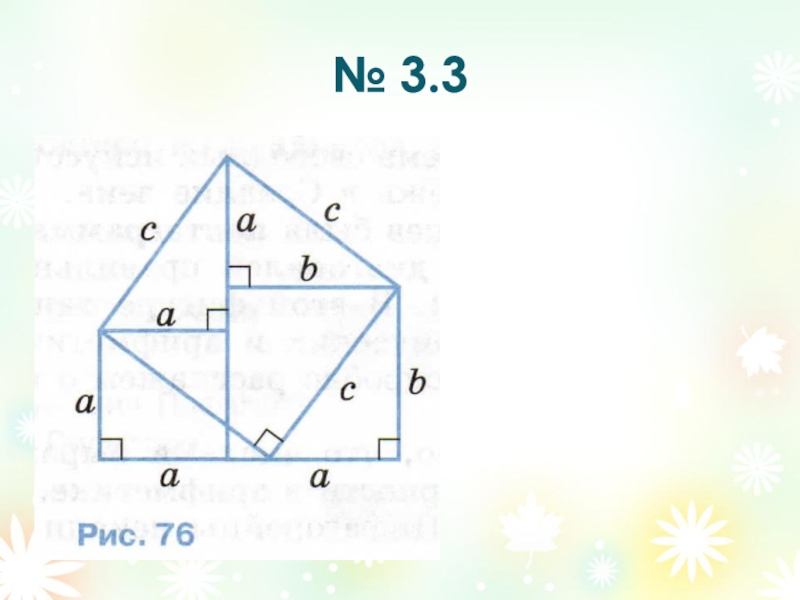
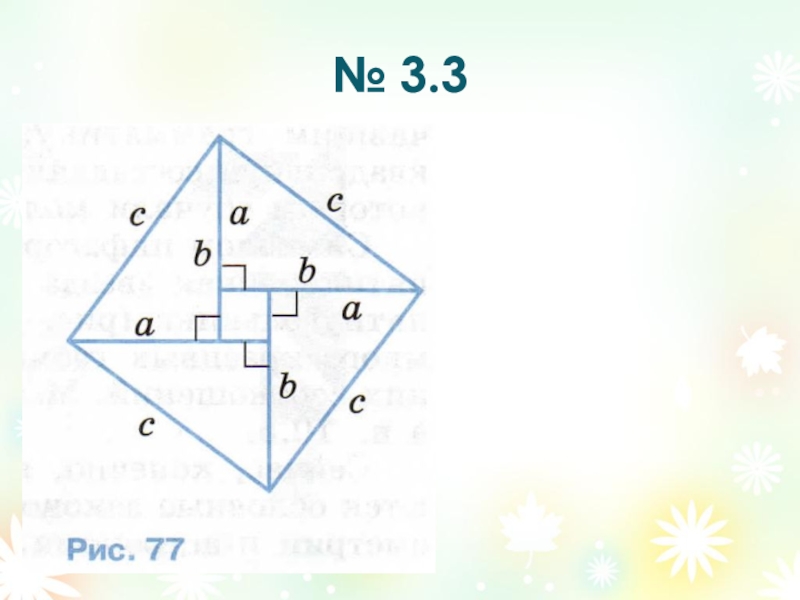
- 23. № 3.3
- 24. № 3.3
- 25. № 3.3
- 26. Определение прямоугольного треугольника.Название сторон прямоугольного треугольника.Как найти
- 27. Домаn. 3.1 №№ 3. 3 (рис. 78), 3.4, 3.5
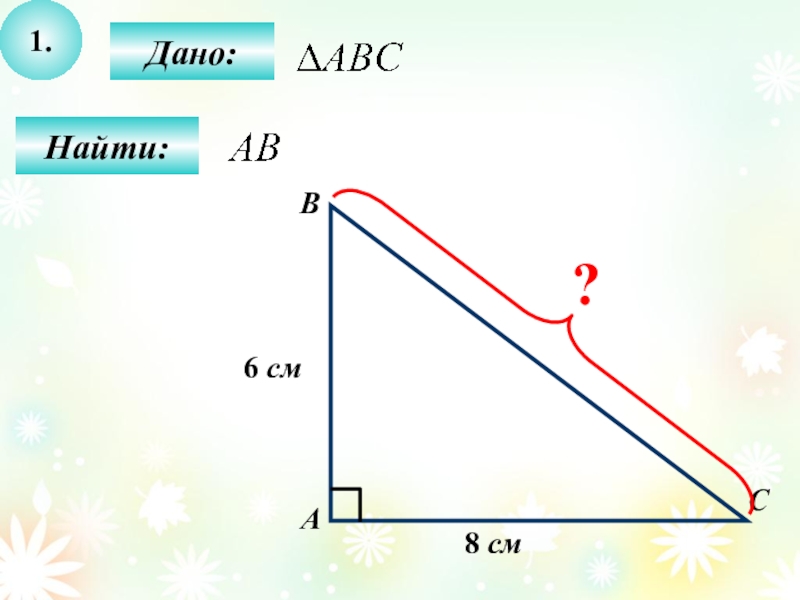
- 28. 1.Найти:СВАДано:8 см6 см?
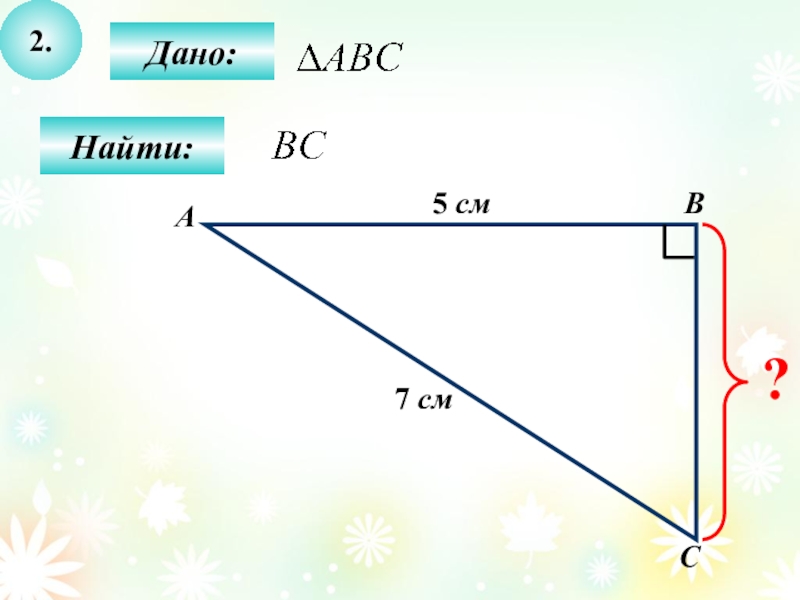
- 29. 2.Дано:СВНайти:А5 см7 см?
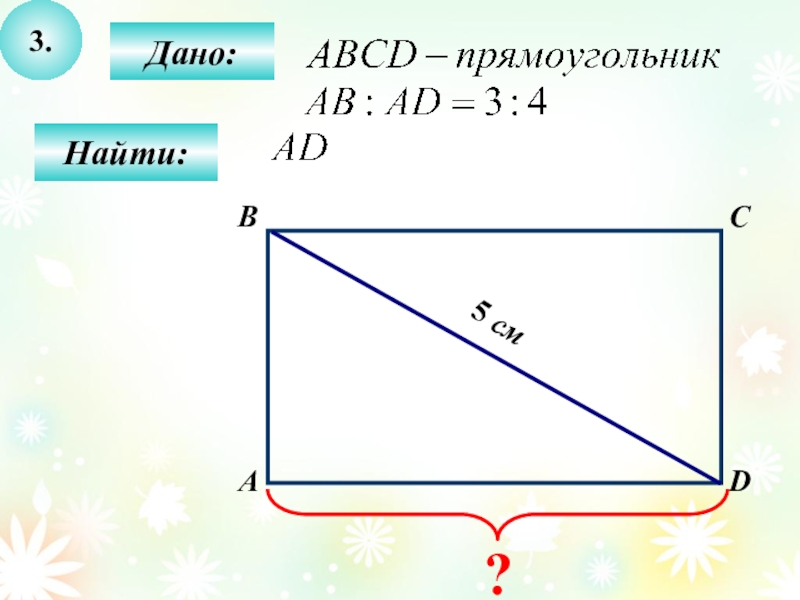
- 30. 3.Дано:АBCDНайти:5 см?
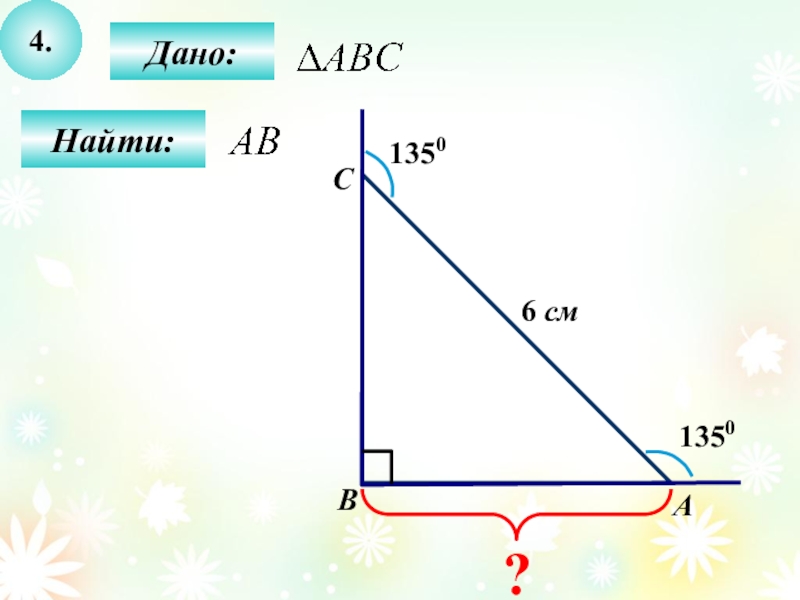
- 31. 4.Дано:Найти:АBC135013506 см?
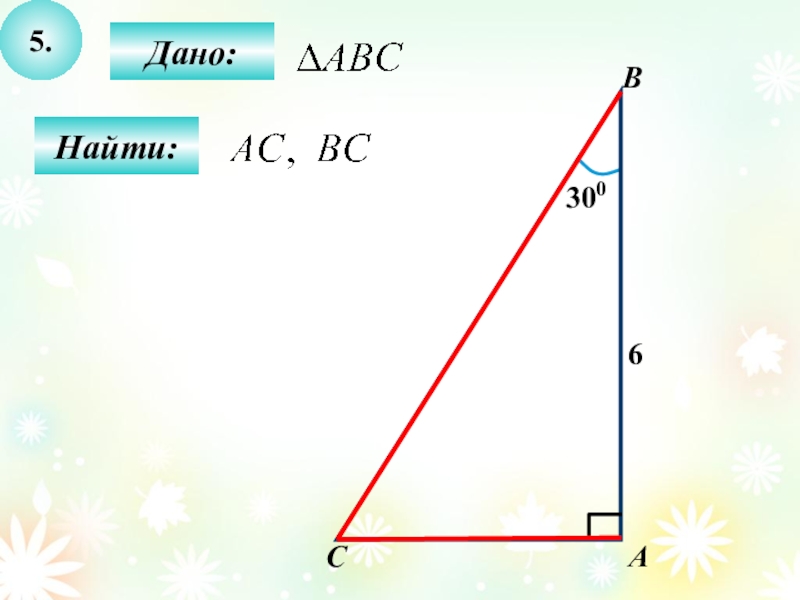
- 32. 5.Дано:Найти:BC6300А
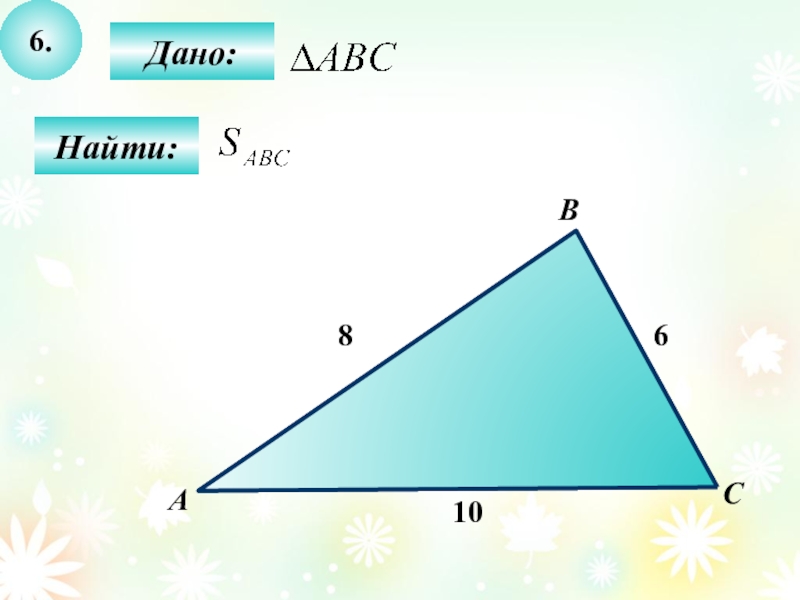
- 33. 6.Найти:АBC8Дано:610
- 34. Слайд 34
- 35. Слайд 35
Слайд 3№ 2. 9
T₁
T₂
S = ½ аb
S(T₁) = ½ 3×5 = 7,5
S(T₂) = ½ 5×5 = 12,5 кв. ед
S(T) = S(T₁) + S(T₂) = 7,5 + 12,5 = 20кв. ед
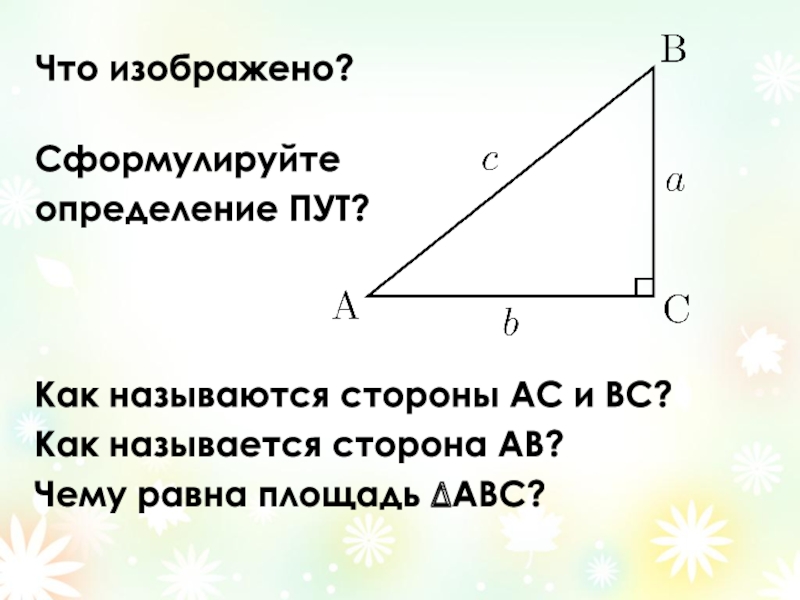
Слайд 7Как называются стороны АС и ВС?
Как называется сторона АВ?
Чему равна площадь
Что изображено?
Сформулируйте
определение ПУТ?
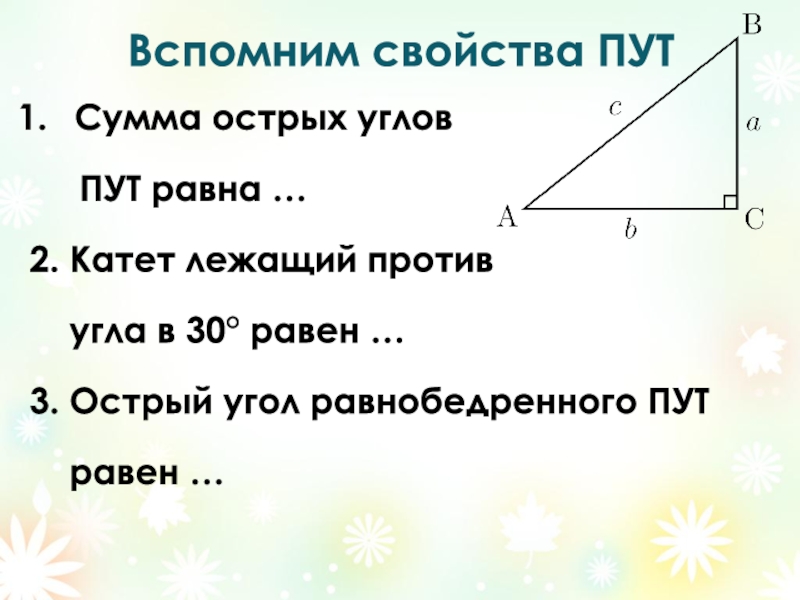
Слайд 8Вспомним свойства ПУТ
Сумма острых углов
ПУТ равна …
2. Катет
угла в 30° равен …
3. Острый угол равнобедренного ПУТ
равен …
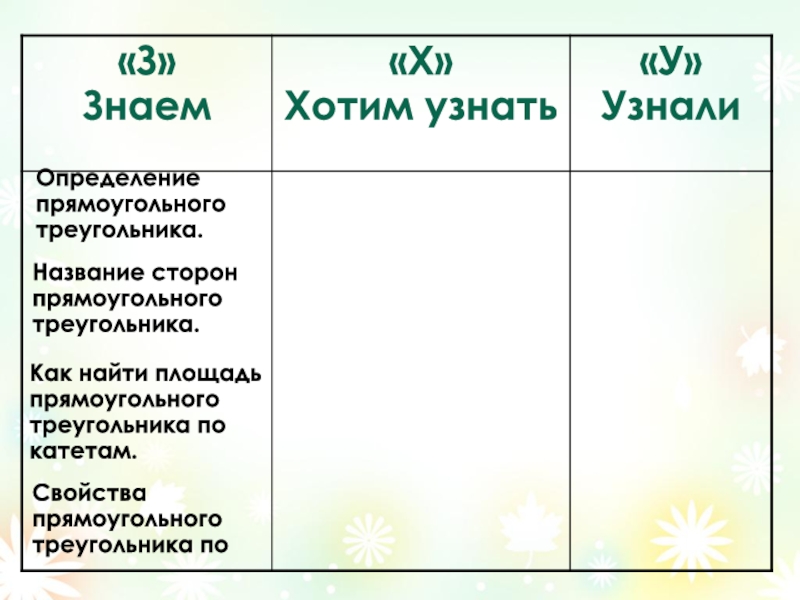
Слайд 9Определение прямоугольного треугольника.
Название сторон прямоугольного треугольника.
Как найти площадь прямоугольного треугольника по
Свойства прямоугольного треугольника по
Слайд 11Определение прямоугольного треугольника.
Название сторон прямоугольного треугольника.
Как найти площадь прямоугольного треугольника по
О чём говорится в теореме Пифагора.
Какие существуют способы доказательства теоремы Пифагора.
Какие решать задачи.
Слайд 12Теорема 1 Пифагора
Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна
Слайд 13Дано: T-пут, a, b – катеты,
Доказать: с² = а² + b²
T
Док - во:
Построим квадрат Р
со стороной а + b
и вершинами А, В, С, D.
Слайд 142. На сторонах этого
квадрат Р отмечены
эти стороны на
отрезки, равные
отрезкам а и b.
3. Соединим
последовательно
точки разбиения
квадрата Р отрезками .
4. Получим разбиение квадрата Р на
4 - ∆ = T, и 1 – F, все стороны = с.
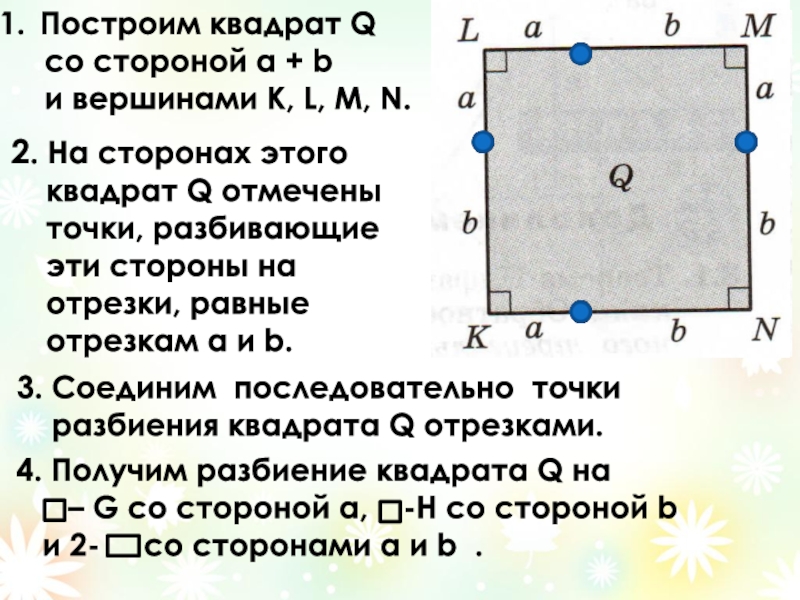
Слайд 16Построим квадрат Q
со стороной а + b
2. На сторонах этого
квадрат Q отмечены
точки, разбивающие
эти стороны на
отрезки, равные
отрезкам а и b.
3. Соединим последовательно точки
разбиения квадрата Q отрезками.
4. Получим разбиение квадрата Q на
– G со стороной а, -Н со стороной b
и 2- со сторонами а и b .
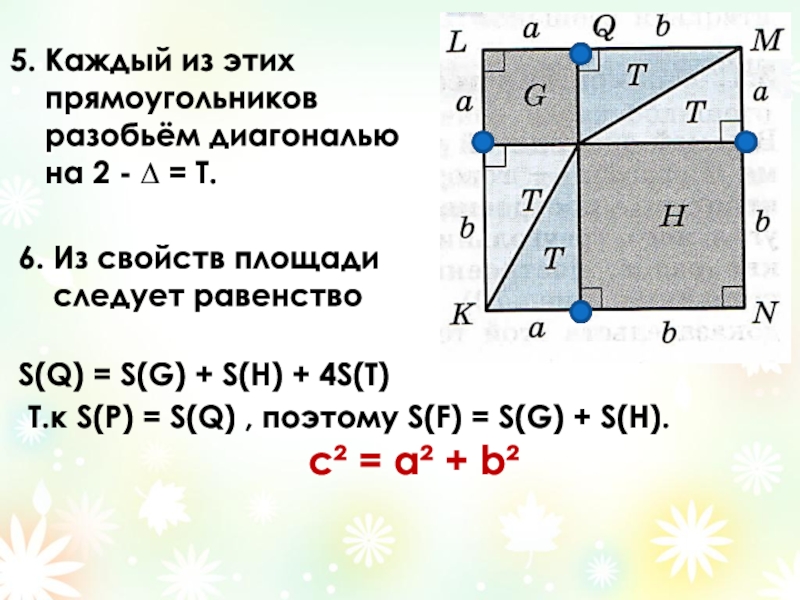
Слайд 175. Каждый из этих
прямоугольников
разобьём диагональю
на 2 - ∆ = T.
6. Из свойств площади
следует равенство
S(Q) = S(G) + S(H) + 4S(T)
Т.к S(Р) = S(Q) , поэтому S(F) = S(G) + S(H).
с² = а² + b²
Слайд 18Теорема 2 Пифагора
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме
с² = а² + b²
Короче:
Квадрат гипотенузы равен сумме квадратов катетов.
Слайд 19Дополняем теорию
Теорема Пифагора – свойство прямоугольного треугольника.
Обратная теорема Пифагора – признак
Слайд 20№ 3.1
Если в треугольнике квадрат
одной из его сторон равен
сумме
других его сторон, то такой
треугольник прямоугольный.
Слайд 21Дано: ∆АВС,
АВ² = АС²
Док – ть: ∆АВС – пу.
Док –во:
Построим пу ∆KLM,
∠ M = 90° и ML, MK – катеты,
ML = CB, MK = CA.
2. По ТП KL² = ML² + MK²
3. Т.к ML = CB, MK = CA, то
АВ² = KL² , поэтому АВ = KL.
4. ∆АВС = ∆KLM по трем сторонам.
5. ∠ С = ∠ M = 90°. Следовательно ∆АВС – пу.
Слайд 22№ 3.2
(3, 4, 5), (6, 8, 10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (16, 30, 34), (21, 28, 35), (12, 35, 37), (15, 36, 39),
Слайд 26Определение прямоугольного треугольника.
Название сторон прямоугольного треугольника.
Как найти площадь прямоугольного треугольника по
О чём говорится в теореме Пифагора.
Какие существуют способы доказательства теоремы Пифагора.
Какие решать задачи.