Презентация, доклад по геометрии на тему Теорема Пифагора (8 класс)

Содержание

1. Презентация по геометрии на тему Теорема Пифагора (8 класс)
2. Слайд 2
3. Теорема Пифагора: Квадрат гипотенузы равен
4. Факт, изложенный в теореме Пифагора, был сначала
5. Посмотрите внимательно на два квадрата, и вам
6. Более сложное доказательство было предложено Евклидом.Чертёж, применяемый
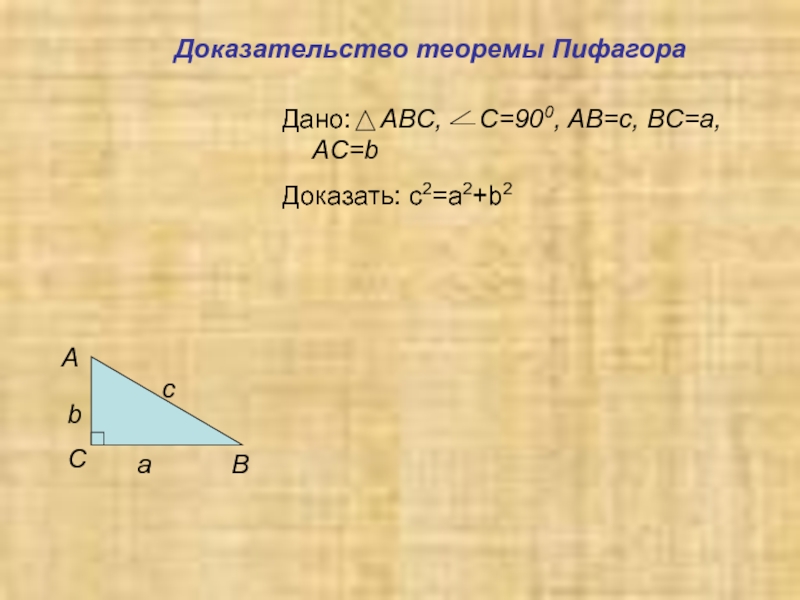
7. Доказательство теоремы ПифагораCBAabcДано: ABC, C=900, AB=c, BC=a, AC=bДоказать: c2=a2+b2
8. 2) BAC= AKE= EPM=
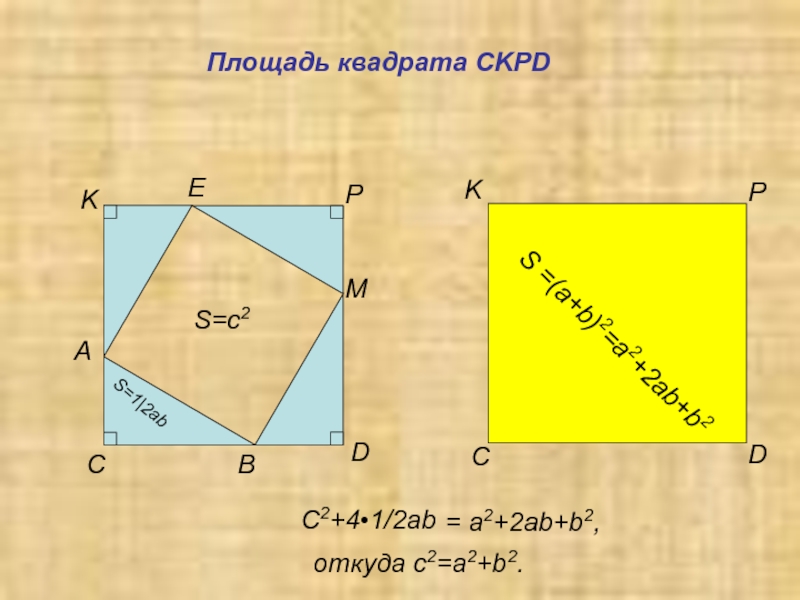
9. откуда c2=a2+b2.Площадь квадрата CKPDC2+4•1/2ab= a2+2ab+b2,
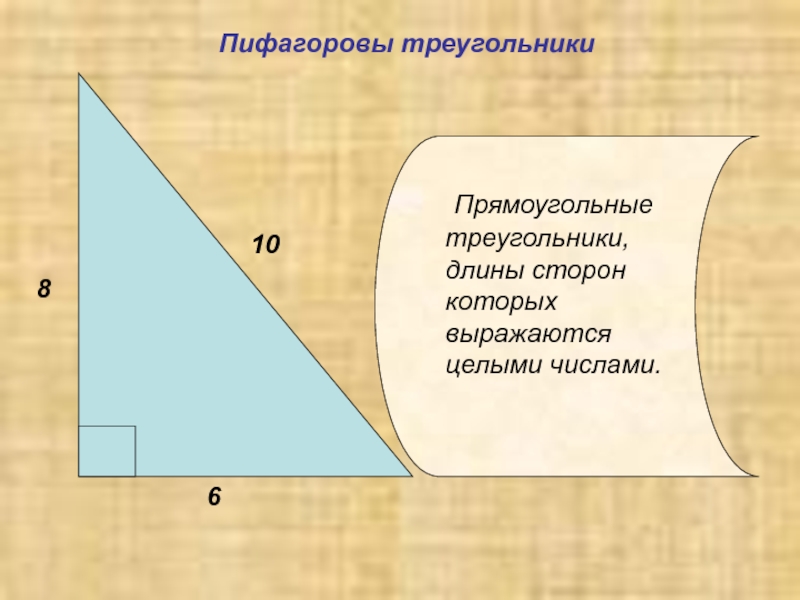
10. Прямоугольные треугольники, длины сторон которых выражаются целыми числами.Пифагоровы треугольники
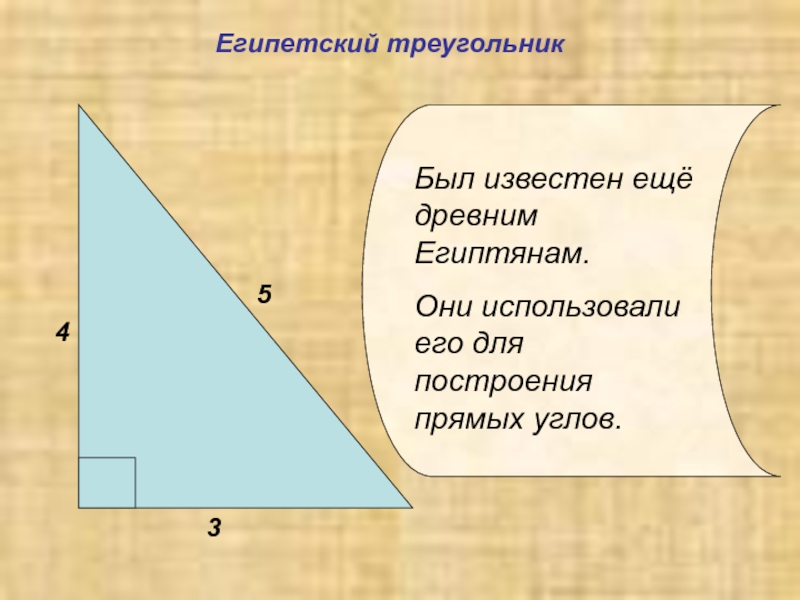
11. Египетский треугольникБыл известен ещё древним Египтянам.Они использовали его для построения прямых углов.
12. 1) Верёвку метками делили на 12 равных
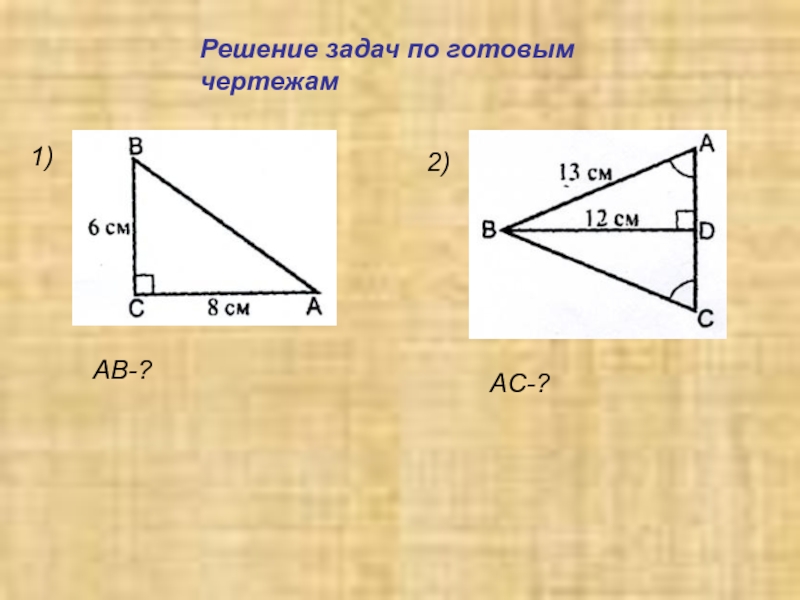
13. Решение задач по готовым чертежам 1)2)AB-?AC-?
14. Решение задач по готовым чертежам 1)2)AB2= AC2+BC2,AB2=100,AB=10.АС-?
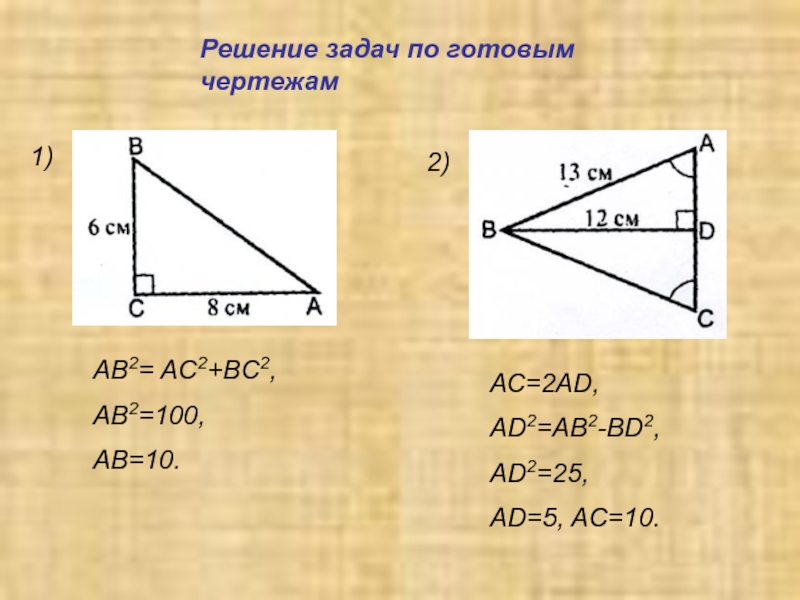
15. Решение задач по готовым чертежам 1)2)AB2= AC2+BC2,AB2=100,AB=10.АС=2AD,AD2=AB2-BD2,AD2=25,AD=5, AC=10.
16. И. Я. Депман Н. Я. Виленкин За

Пифагор (ок. 570- ок. 500 гг. до н. э.)Родился вVI веке до н. э. на греческом

Главная
Геометрия
Презентация по геометрии на тему Теорема Пифагора (8 класс)

Слайд 1

Теорема Пифагора
Урок геометрии 8 класс
Преподаватель: Белова И.А. МОУ «Гимназия

№13

Теорема Пифагора Урок геометрии 8 класс Преподаватель: Белова И.А. МОУ «Гимназия №13

Слайд 2

Пифагор
(ок. 570- ок. 500 гг. до н. э.)

Родился вVI веке до н. э. на греческом острове Самос.
Пифагор
-разделил числа на чётные, нечётные, простые, составные;
-доказал, что не является рациональным числом;
-обнаружил, что сумма величин углов треугольника 1800;
-доказал теорему, ставшую в дальнейшем основой применения численных методов в геометрии.

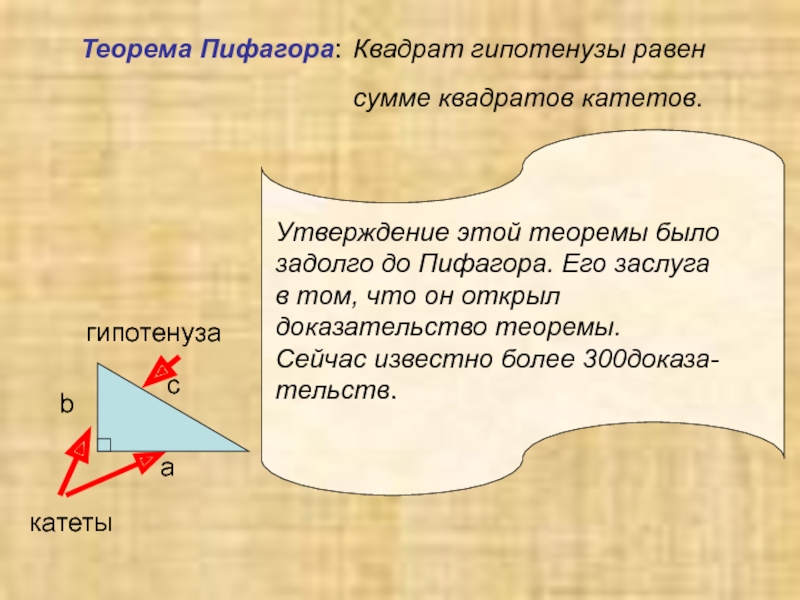
Слайд 3Теорема Пифагора: Квадрат гипотенузы равен

сумме квадратов катетов.

Утверждение этой теоремы было
задолго до Пифагора. Его заслуга
в том, что он открыл доказательство теоремы.
Сейчас известно более 300доказа-тельств.

катеты

гипотенуза

Теорема Пифагора: Квадрат гипотенузы равен

Слайд 4

Факт, изложенный в теореме Пифагора, был сначала
установлен для равнобедренных прямоугольных

треугольников. Достаточно взглянуть на мозаику из чёрных
и светлых треугольников.

Факт, изложенный в теореме Пифагора, был сначала установлен для равнобедренных прямоугольных треугольников. Достаточно взглянуть на мозаику из

Слайд 5

Посмотрите внимательно на два квадрата, и вам всё станет ясно.
Индусы к

этому чертежу добавляли лишь одно слово: «Смотри!»

Посмотрите внимательно на два квадрата, и вам всё станет ясно.Индусы к этому чертежу добавляли лишь одно слово:

Слайд 6
Более сложное доказательство было предложено Евклидом.
Чертёж, применяемый при доказательстве этой теоремы,

в шутку называли «Пифагоровы штаны».

«Пифагоровы штаны, на все стороны равны»

Более сложное доказательство было предложено Евклидом.Чертёж, применяемый при доказательстве этой теоремы, в шутку называли «Пифагоровы штаны».«Пифагоровы штаны,

Слайд 7Доказательство теоремы Пифагора
C
B
A
a
b
c
Дано: ABC, C=900, AB=c, BC=a, AC=b
Доказать:

c2=a2+b2

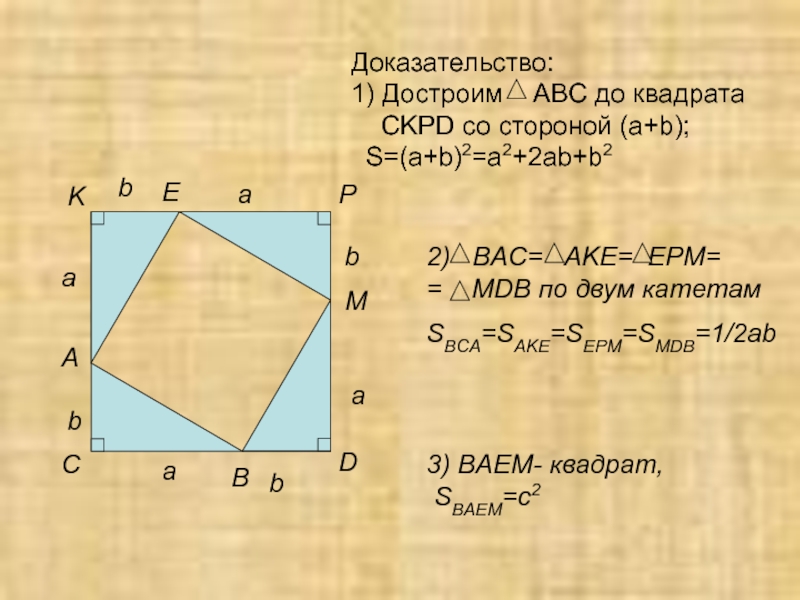
Слайд 82) BAC= AKE= EPM= =

MDB по двум катетам
SBCA=SAKE=SEPM=SMDB=1/2ab

Доказательство:
1) Достроим ABC до квадрата CKPD со стороной (a+b);
S=(a+b)2=a2+2ab+b2

3) BAEM- квадрат,
SBAEM=c2

2) BAC= AKE= EPM= = MDB по двум катетамSBCA=SAKE=SEPM=SMDB=1/2abДоказательство: 1) Достроим

Слайд 9
откуда c2=a2+b2.
Площадь квадрата CKPD
C2+4•1/2ab
= a2+2ab+b2,

Слайд 10

Прямоугольные треугольники, длины сторон которых выражаются целыми числами.

Пифагоровы треугольники

Слайд 11Египетский треугольник

Был известен ещё древним Египтянам.
Они использовали его для построения прямых

углов.

Слайд 12
1) Верёвку метками делили на 12 равных частей;
2) связывали концы верёвок;
3)

растягивали на земле с помощью кольев в виде треугольника со сторонами 3, 4, 5;
4) угол, между сторонами, равными 3 и 4, оказывался прямым.

1) Верёвку метками делили на 12 равных частей;2) связывали концы верёвок;3) растягивали на земле с помощью кольев

Слайд 13Решение задач по готовым чертежам

1)
2)
AB-?
AC-?

Слайд 14Решение задач по готовым чертежам

1)
2)
AB2= AC2+BC2,
AB2=100,
AB=10.
АС-?

Слайд 15Решение задач по готовым чертежам

1)
2)
AB2= AC2+BC2,
AB2=100,
AB=10.
АС=2AD,
AD2=AB2-BD2,
AD2=25,
AD=5, AC=10.

Слайд 16
И. Я. Депман Н. Я. Виленкин За страницами учебника математики:- М.:

Просвещение,1989.
Л.С. Атанасян, В.Ф. Бутузов Геометрия, 7-9:- М.: Просвещение, 2013.
Л. С. Атанасян Изучение геометрии в 7, 8, 9, классах: Метод. Рекомендации к учеб. : Книга для учителя:- М. : Просвещение, 2002.
А. П. Савин Энциклопедический словарь юного математика:- М.: Педагогика, 1989.
А. П. Савин Я познаю мир: Детская энциклопедия: Математика:- М.: Аст. : 1997.

И. Я. Депман Н. Я. Виленкин За страницами учебника математики:- М.: Просвещение,1989.Л.С. Атанасян, В.Ф. Бутузов Геометрия, 7-9:-

Скачать презентацию

Презентация, доклад по геометрии на тему Теорема Пифагора (8 класс)

Содержание

Слайд 1

Теорема Пифагора
Урок геометрии 8 класс
Преподаватель: Белова И.А. МОУ «Гимназия

Слайд 2

Слайд 3Теорема Пифагора: Квадрат гипотенузы равен

Слайд 4

Факт, изложенный в теореме Пифагора, был сначала
установлен для равнобедренных прямоугольных

Слайд 5

Посмотрите внимательно на два квадрата, и вам всё станет ясно.
Индусы к

Слайд 6
Более сложное доказательство было предложено Евклидом.
Чертёж, применяемый при доказательстве этой теоремы,

Слайд 7Доказательство теоремы Пифагора
C
B
A
a
b
c
Дано: ABC, C=900, AB=c, BC=a, AC=b
Доказать:

Слайд 82) BAC= AKE= EPM= =

Слайд 9
откуда c2=a2+b2.
Площадь квадрата CKPD
C2+4•1/2ab
= a2+2ab+b2,

Слайд 10

Прямоугольные треугольники, длины сторон которых выражаются целыми числами.

Пифагоровы треугольники

Слайд 11Египетский треугольник

Был известен ещё древним Египтянам.
Они использовали его для построения прямых

Слайд 12
1) Верёвку метками делили на 12 равных частей;
2) связывали концы верёвок;
3)

Слайд 13Решение задач по готовым чертежам

1)
2)
AB-?
AC-?

Слайд 14Решение задач по готовым чертежам

1)
2)
AB2= AC2+BC2,
AB2=100,
AB=10.
АС-?

Слайд 15Решение задач по готовым чертежам

1)
2)
AB2= AC2+BC2,
AB2=100,
AB=10.
АС=2AD,
AD2=AB2-BD2,
AD2=25,
AD=5, AC=10.

Слайд 16
И. Я. Депман Н. Я. Виленкин За страницами учебника математики:- М.:

Что такое shareslide.ru?

Обратная связь

Презентация, доклад по геометрии на тему Теорема Пифагора (8 класс)

Содержание

Слайд 1Теорема Пифагора Урок геометрии 8 класс Преподаватель: Белова И.А. МОУ «Гимназия

Слайд 2

Слайд 3Теорема Пифагора: Квадрат гипотенузы равен

Слайд 4Факт, изложенный в теореме Пифагора, был сначала установлен для равнобедренных прямоугольных

Слайд 5Посмотрите внимательно на два квадрата, и вам всё станет ясно.Индусы к

Слайд 6Более сложное доказательство было предложено Евклидом.Чертёж, применяемый при доказательстве этой теоремы,

Слайд 7Доказательство теоремы ПифагораCBAabcДано: ABC, C=900, AB=c, BC=a, AC=bДоказать:

Слайд 82) BAC= AKE= EPM= =

Слайд 9откуда c2=a2+b2.Площадь квадрата CKPDC2+4•1/2ab= a2+2ab+b2,

Слайд 10 Прямоугольные треугольники, длины сторон которых выражаются целыми числами.Пифагоровы треугольники

Слайд 11Египетский треугольникБыл известен ещё древним Египтянам.Они использовали его для построения прямых

Слайд 121) Верёвку метками делили на 12 равных частей;2) связывали концы верёвок;3)

Слайд 13Решение задач по готовым чертежам 1)2)AB-?AC-?

Слайд 14Решение задач по готовым чертежам 1)2)AB2= AC2+BC2,AB2=100,AB=10.АС-?

Слайд 15Решение задач по готовым чертежам 1)2)AB2= AC2+BC2,AB2=100,AB=10.АС=2AD,AD2=AB2-BD2,AD2=25,AD=5, AC=10.

Слайд 16И. Я. Депман Н. Я. Виленкин За страницами учебника математики:- М.:

Похожие презентации

Что такое shareslide.ru?

Обратная связь

Слайд 1

Теорема Пифагора
Урок геометрии 8 класс
Преподаватель: Белова И.А. МОУ «Гимназия

Слайд 4

Факт, изложенный в теореме Пифагора, был сначала
установлен для равнобедренных прямоугольных

Слайд 5

Посмотрите внимательно на два квадрата, и вам всё станет ясно.
Индусы к

Слайд 6
Более сложное доказательство было предложено Евклидом.
Чертёж, применяемый при доказательстве этой теоремы,

Слайд 7Доказательство теоремы Пифагора
C
B
A
a
b
c
Дано: ABC, C=900, AB=c, BC=a, AC=b
Доказать:

Слайд 9
откуда c2=a2+b2.
Площадь квадрата CKPD
C2+4•1/2ab
= a2+2ab+b2,

Слайд 10

Прямоугольные треугольники, длины сторон которых выражаются целыми числами.

Пифагоровы треугольники

Слайд 11Египетский треугольник

Был известен ещё древним Египтянам.
Они использовали его для построения прямых

Слайд 12
1) Верёвку метками делили на 12 равных частей;
2) связывали концы верёвок;
3)

Слайд 13Решение задач по готовым чертежам

1)
2)
AB-?
AC-?

Слайд 14Решение задач по готовым чертежам

1)
2)
AB2= AC2+BC2,
AB2=100,
AB=10.
АС-?

Слайд 15Решение задач по готовым чертежам

1)
2)
AB2= AC2+BC2,
AB2=100,
AB=10.
АС=2AD,
AD2=AB2-BD2,
AD2=25,
AD=5, AC=10.

Слайд 16
И. Я. Депман Н. Я. Виленкин За страницами учебника математики:- М.: