против другой. Высота одной 30 локтей, другой – 20 локтей. Расстояние между их основаниями – 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами. Они кинулись к ней разом и достигли ее одновременно. На каком расстоянии от более высокой пальмы появилась рыба?
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Теорема Пифагора (8 класс)
Содержание
- 1. Презентация по геометрии на тему Теорема Пифагора (8 класс)
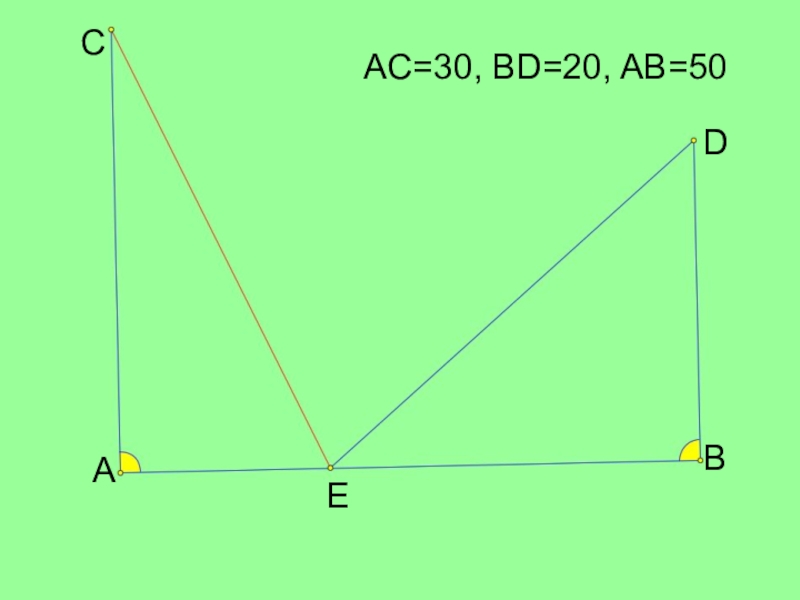
- 2. AC=30, BD=20, AB=50ABCED
- 3. Построить прямоугольный треугольник по катетам, измерить гипотенузу10 см17 см5 см
- 4. Слайд 4
- 5. Теорема Пифагора:В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.ABCbсаa²+b²=c²
- 6. Немного истории… Пифагор Самосский
- 7. Пифагорейская школа Вернувшись на родину,
- 8. Заповеди пифагорейцевДелать то, что
- 9. Доказательство теоремы ПифагораG08_031_i01 (1).oms
- 10. А сейчас вернемся к нашей задаче
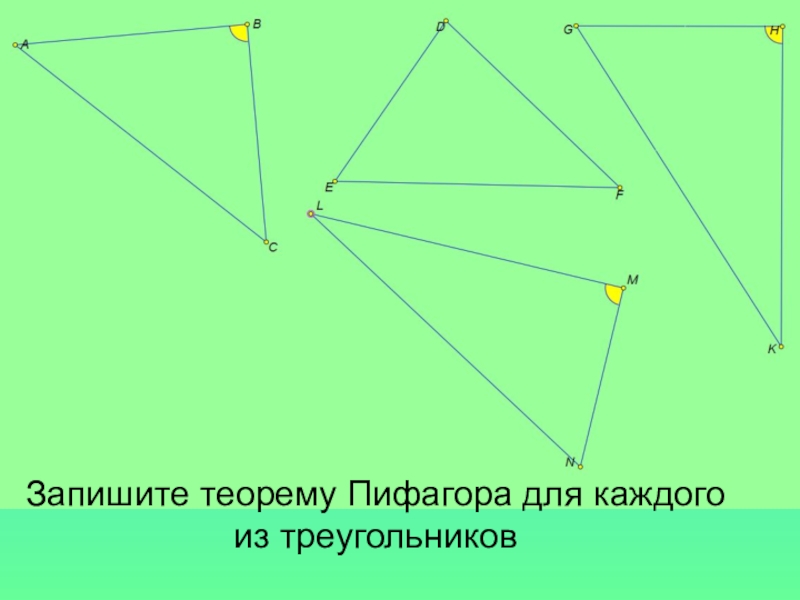
- 11. Запишите теорему Пифагора для каждого из треугольников
- 12. Прямоугольный треугольникa и b - катетыс –
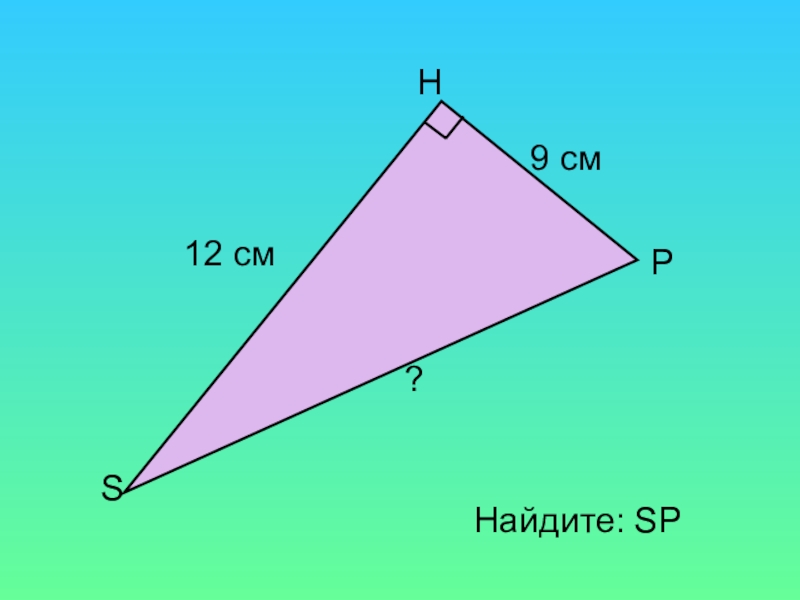
- 13. Найдите: SP
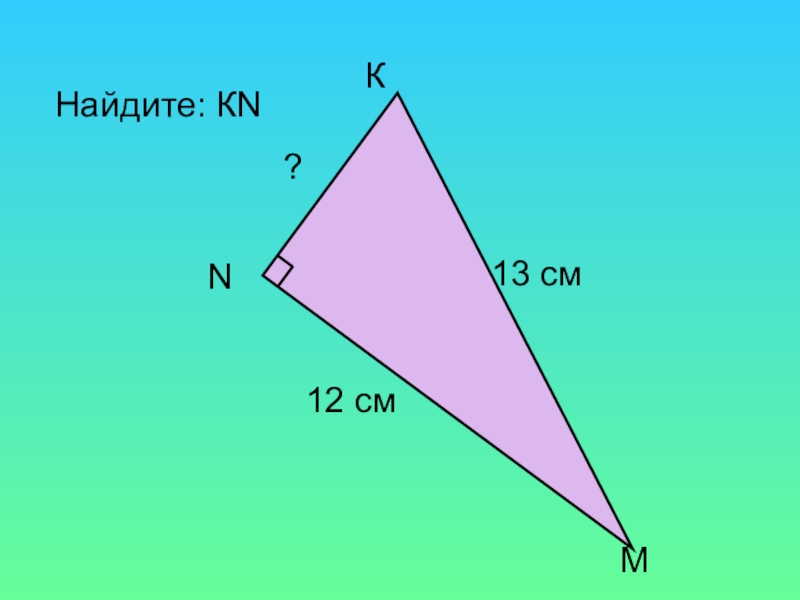
- 14. Найдите: КN
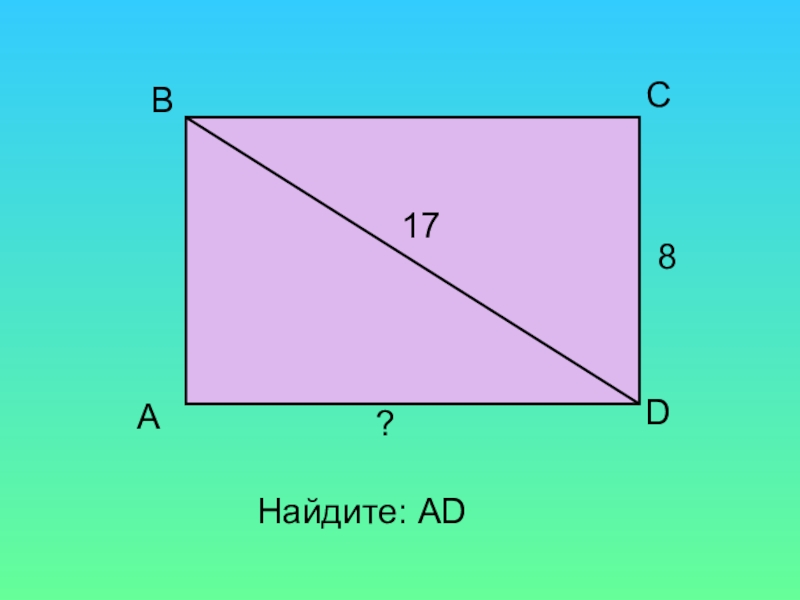
- 15. Найдите: АD
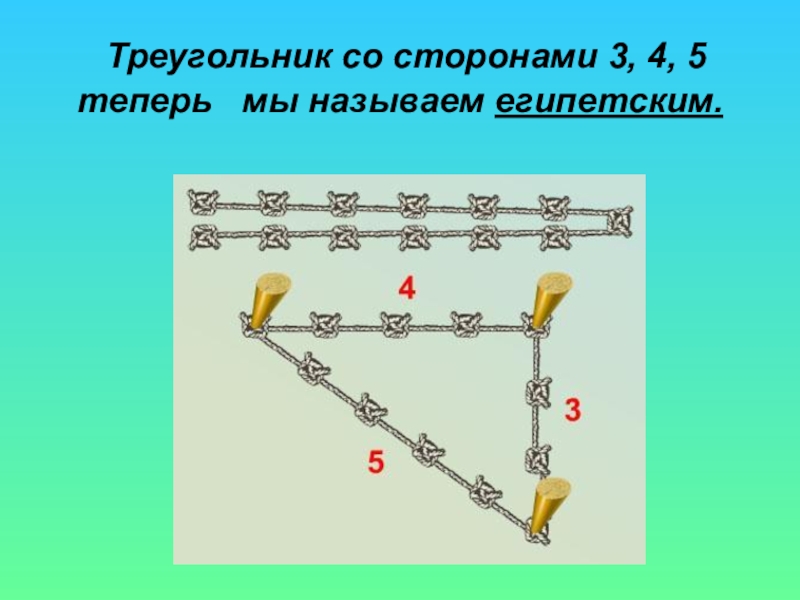
- 16. Треугольник со сторонами 3, 4, 5 теперь мы называем египетским.
- 17. «Геометрия владеет многими сокровищами, но одно из
- 18. Домашнее задание:п.54 ; №483(в, г), №484
AC=30, BD=20, AB=50ABCED
Слайд 5Теорема Пифагора:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
A
B
C
b
с
а
a²+b²=c²
Слайд 6Немного истории…
Пифагор Самосский
( 570—490 гг. до
н. э.) — древнегреческий философ и математик, создатель религиозно-философской школы пифагорейцев.
Слайд 7Пифагорейская школа
Вернувшись на родину, Пифагор организовал кружок
молодежи из
представителей аристократии.
Так на юге Италии, которая была тогда греческой колонией, возникла
пифагорейская школа.
представителей аристократии.
Так на юге Италии, которая была тогда греческой колонией, возникла
пифагорейская школа.
Слайд 8 Заповеди пифагорейцев
Делать то, что впоследствии не огорчит тебя
и не принудит раскаиваться;
Не делай никогда того, что не знаешь, но научись всему, что следует знать;
Не пренебрегай здоровьем своего тела;
Приучайся жить просто и без роскоши.
Не делай никогда того, что не знаешь, но научись всему, что следует знать;
Не пренебрегай здоровьем своего тела;
Приучайся жить просто и без роскоши.
Слайд 10А сейчас вернемся к нашей задаче
На обоих берегах реки
растет по пальме, одна против другой. Высота одной 30 локтей, другой – 20 локтей. Расстояние между их основаниями – 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами. Они кинулись к ней разом и достигли ее одновременно. На каком расстоянии от более высокой пальмы появилась рыба?
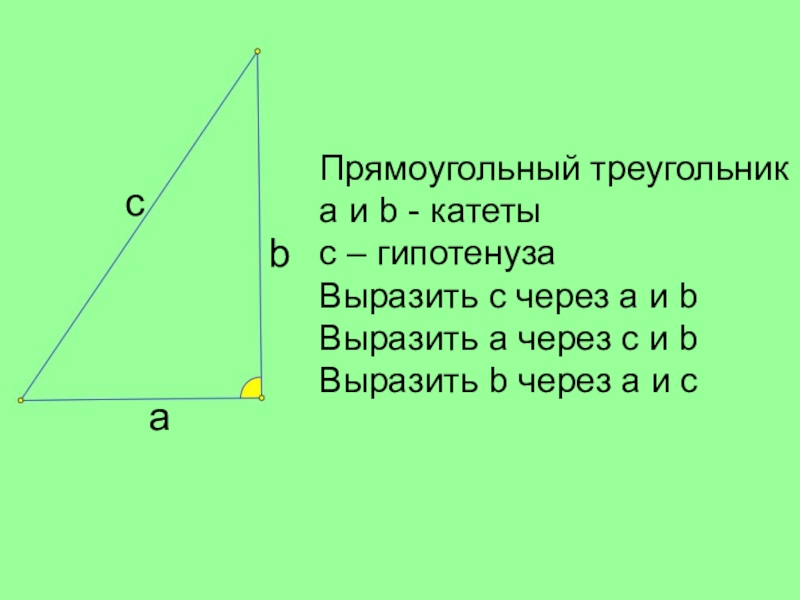
Слайд 12Прямоугольный треугольник
a и b - катеты
с – гипотенуза
Выразить с через a
и b
Выразить a через с и b
Выразить b через a и с
Выразить a через с и b
Выразить b через a и с
a
b
c
Слайд 17«Геометрия владеет многими сокровищами, но одно из главных сокровищ- это теорема
Пифагора».
Иоганн Кеплер
Слайд 18Домашнее задание:
п.54 ; №483(в, г), №484 (б, г, е)
Дополнительное задание:
Найти ещё какой-нибудь способ доказательства теоремы Пифагора.