- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Свойства равнобедренного треугольника 7 класс
Содержание
- 1. Презентация по геометрии на тему Свойства равнобедренного треугольника 7 класс
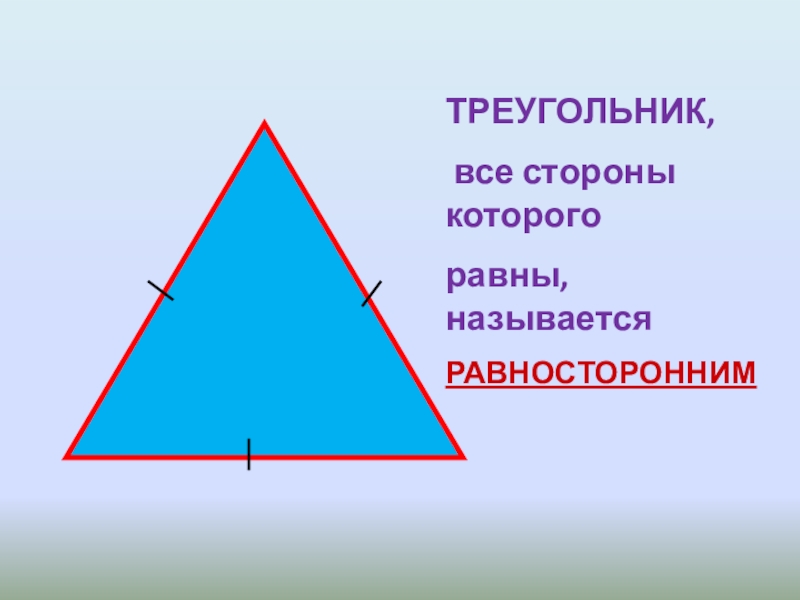
- 2. ТРЕУГОЛЬНИК, все стороны которого равны, называется РАВНОСТОРОННИМ
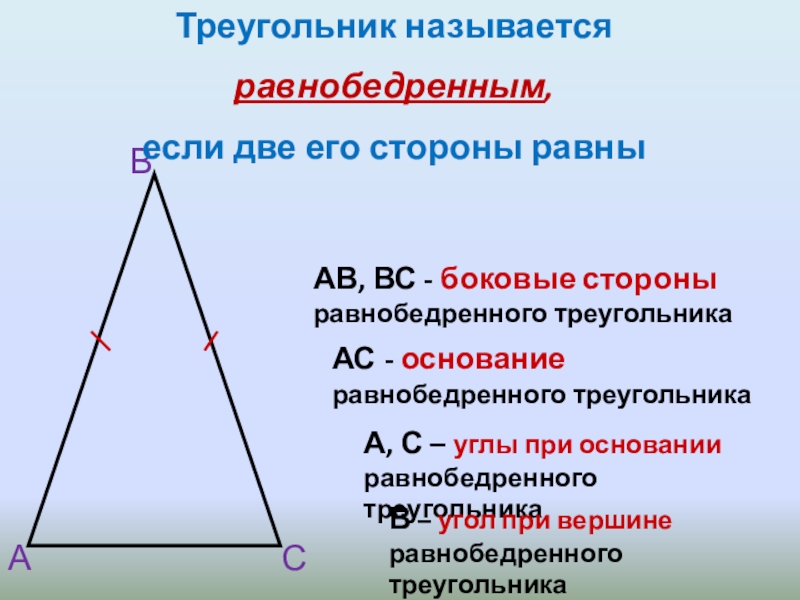
- 3. АВСАВ, ВС - боковые стороны равнобедренного треугольникаА,
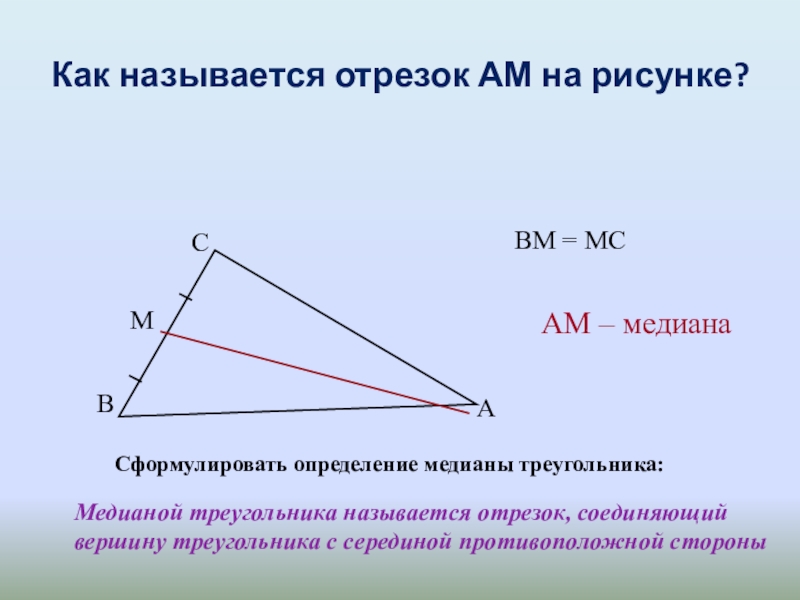
- 4. Как называется отрезок АМ на рисунке?Сформулировать определение
- 5. Как называется отрезок ВК на рисунке?Сформулировать определение
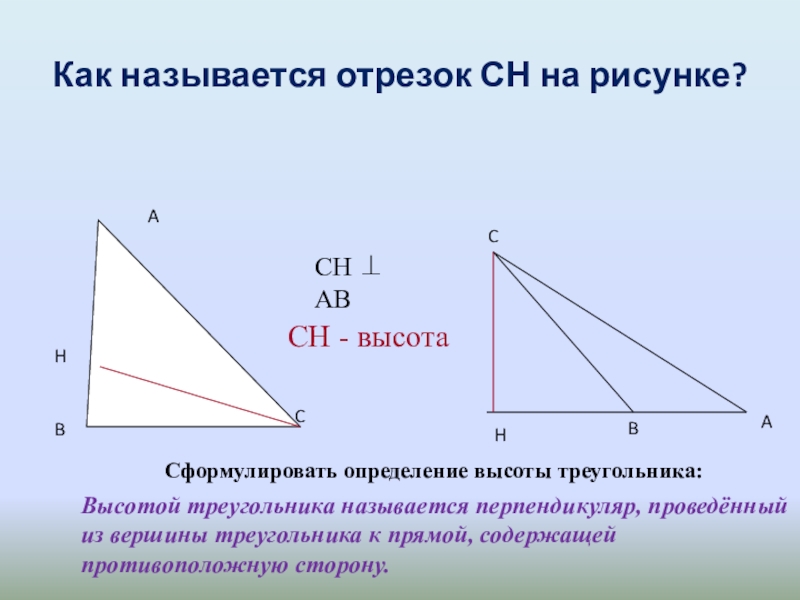
- 6. Как называется отрезок СН на рисунке?Сформулировать определение
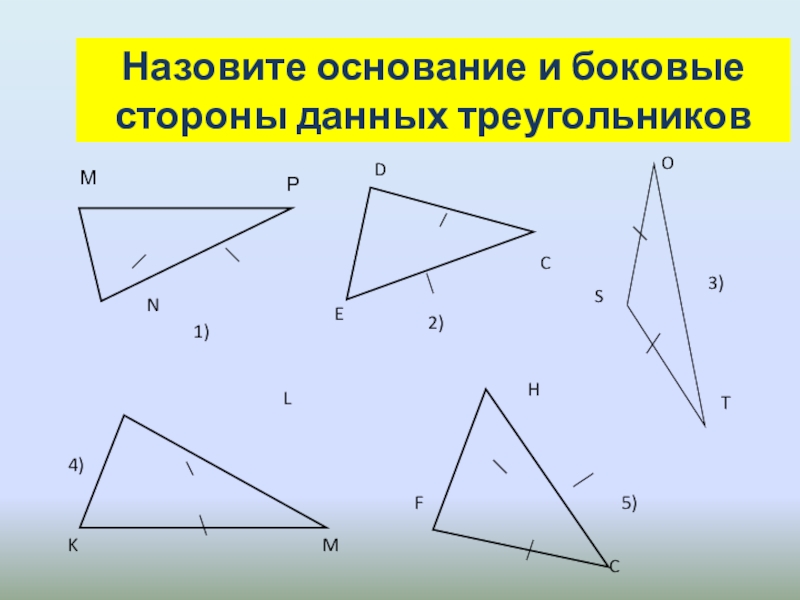
- 7. Назовите основание и боковые стороны данных треугольников
- 8. Теорема 1В равнобедренном треугольнике углыпри основании равныДано:
- 9. Доказательство:Проведём ВD – биссектрису ΔАВС2. Рассмотрим ΔАВD
- 10. Теорема 2В равнобедренном треугольнике биссектриса, проведённая к
- 11. Доказательство:Рассмотрим ΔАВD и ΔСВD
- 12. 40°70°ABCДано: ∆MNP - равнобедренный,NК – биссектрисаNК =
- 13. 40°70°ABCДано: ∆MNP - равнобедренный,NК – биссектрисаNК =
- 14. ДОМАШНЕЕ ЗАДАНИЕП. 18 теоремы, №109, №117 –
Слайд 3
А
В
С
АВ, ВС - боковые стороны равнобедренного треугольника
А, С – углы при
АС - основание равнобедренного треугольника
В – угол при вершине равнобедренного треугольника
Треугольник называется
равнобедренным,
если две его стороны равны
Слайд 4Как называется отрезок АМ на рисунке?
Сформулировать определение медианы треугольника:
Медианой треугольника называется
АМ – медиана
ВМ = МС
Слайд 5Как называется отрезок ВК на рисунке?
Сформулировать определение биссектрисы треугольника:
Биссектрисой треугольника называется
ВК - биссектриса
∠АВК = ∠СВК
Слайд 6Как называется отрезок СН на рисунке?
Сформулировать определение высоты треугольника:
Высотой треугольника называется
СН - высота
СН ⊥ АВ
Слайд 8Теорема 1
В равнобедренном треугольнике углы
при основании равны
Дано: ΔАВС – равнобедренный,
Доказать: ∠А =∠С
Слайд 9Доказательство:
Проведём ВD – биссектрису ΔАВС
2. Рассмотрим ΔАВD и ΔСВD
3. В равных треугольниках против равных сторон лежат равные углы ∠А=∠С
Теорема доказана
Слайд 10Теорема 2
В равнобедренном треугольнике биссектриса, проведённая к основанию,
является медианой и высотой
Дано:
АС – основание,
ВD – биссектриса.
Доказать: 1. ВD – медиана
2. ВD – высота
Слайд 11Доказательство:
Рассмотрим ΔАВD и ΔСВD
АВ=ВС, ВD-общая, ∠АВD=∠СВD, значит
2. В равных треугольниках против равных углов лежат равные стороны АD=DC, значит D – середина АС, следовательно
ВD – медиана
3. В равных треугольниках против равных сторон лежат равные углы , т.е. ∠3=∠4 и ∠3 и ∠4 – смежные, значит ∠3 = ∠4 = 90°, следовательно ВD⊥АС , т.е.
ВD – высота
Теорема доказана
Слайд 12
40°
70°
A
B
C
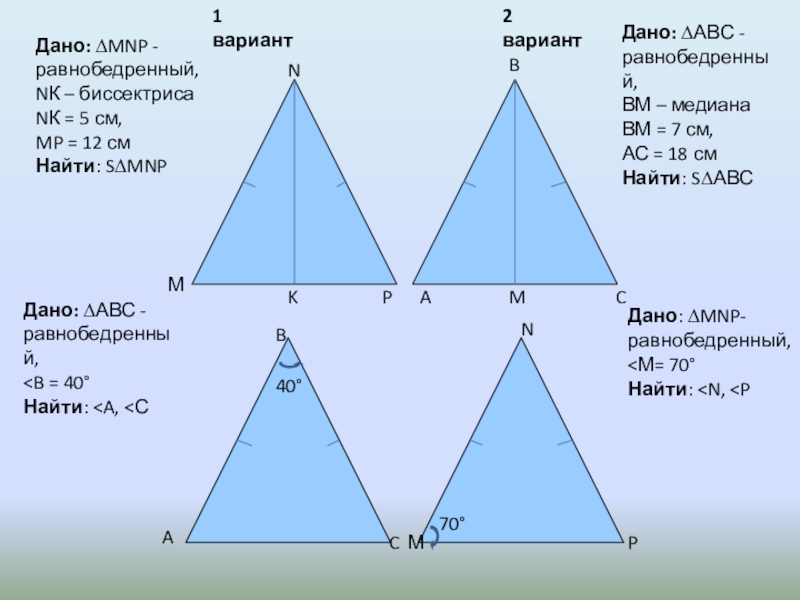
Дано: ∆MNP - равнобедренный,
NК – биссектриса
NК = 5 см,
MP = 12
Найти: S∆MNP
Дано: ∆АВС - равнобедренный,
ВМ – медиана
ВМ = 7 см,
АС = 18 см
Найти: S∆АВС
М
N
P
A
B
C
M
М
N
P
K
Дано: ∆АВС - равнобедренный, Дано: ∆MNP- равнобедренный, 1 вариант 2 вариант
Найти:
<М= 70°
Найти:
Слайд 13
40°
70°
A
B
C
Дано: ∆MNP - равнобедренный,
NК – биссектриса
NК = 5 см,
MP = 12
Найти: S∆MNP
Дано: ∆АВС - равнобедренный,
ВМ – медиана
ВМ = 7 см,
АС = 18 см
Найти: S∆АВС
М
N
P
A
B
C
M
М
N
P
K
Дано: ∆АВС - равнобедренный, Дано: ∆MNP- равнобедренный, 1 вариант 2 вариант NK-высота, NK·MP S = 30 Решение: ВМ-высота, ВМ·АС S = 63 Решение: Решение Решение <А =<С =(180-40): 2 =70° <А =<С =70° <М =<Р =70°
Найти:
<М= 70°
Найти:
S =
S =
Слайд 14ДОМАШНЕЕ ЗАДАНИЕ
П. 18 теоремы,
№109, №117 – из учебника
Р.т. №8
Дополнительная задача:
треугольнике медиана,
проведённая к основанию
является биссектрисой и высотой.