- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Средняя линия треугольника
Содержание
- 1. Презентация по геометрии на тему Средняя линия треугольника
- 2. ОпределениеACBMNAM=MB, BN=NCMN – средняя линия
- 3. Теорема о средней линии треугольникаДано: MN –
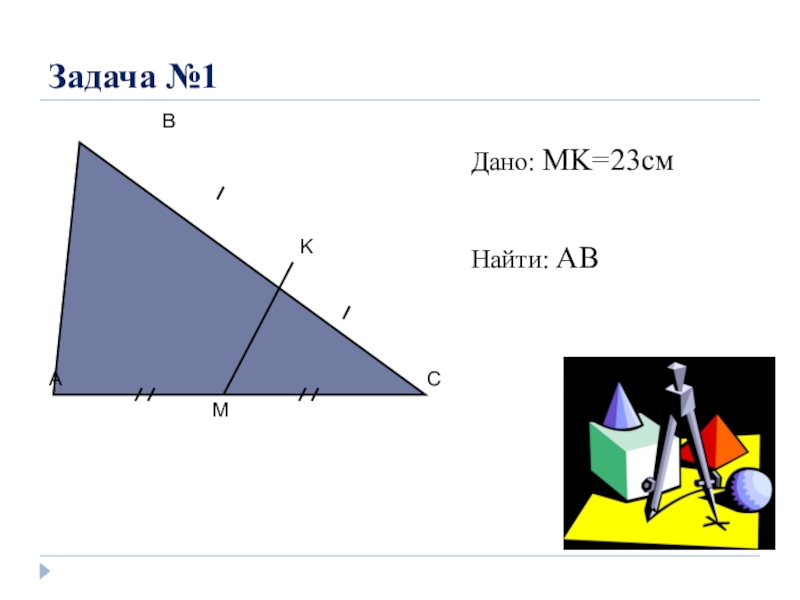
- 4. Задача №1ACBMKДано: MK=23см Найти: AB
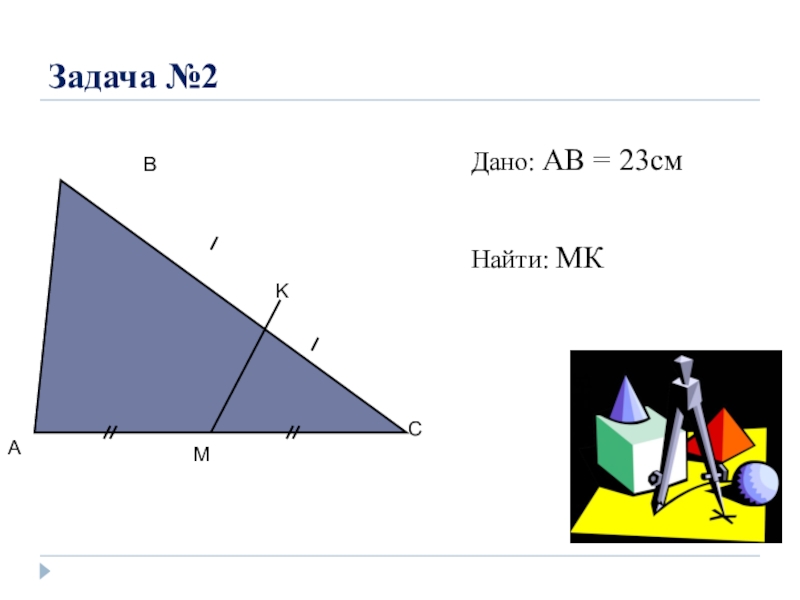
- 5. Задача №2ACBMKДано: АВ = 23см Найти: МК
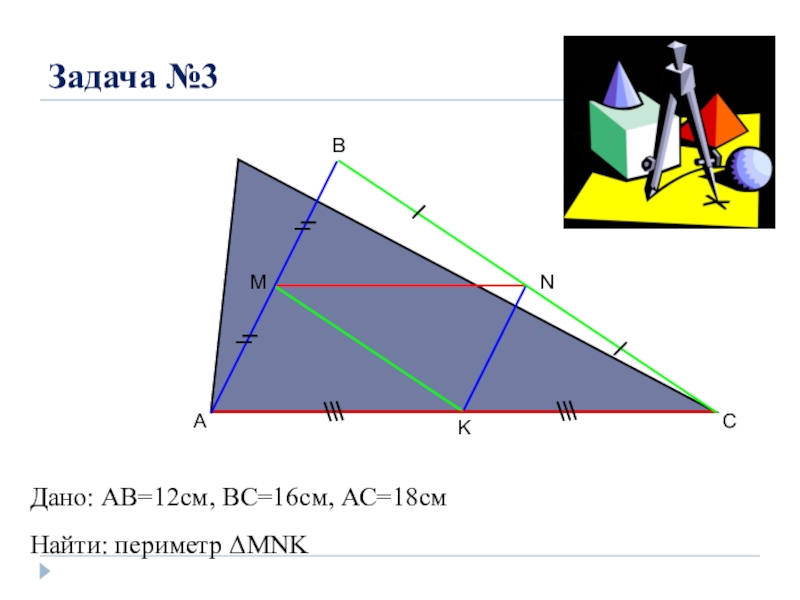
- 6. Задача №3ABCMNKДано: AB=12cм, ВС=16см, АС=18смНайти: периметр ΔMNK
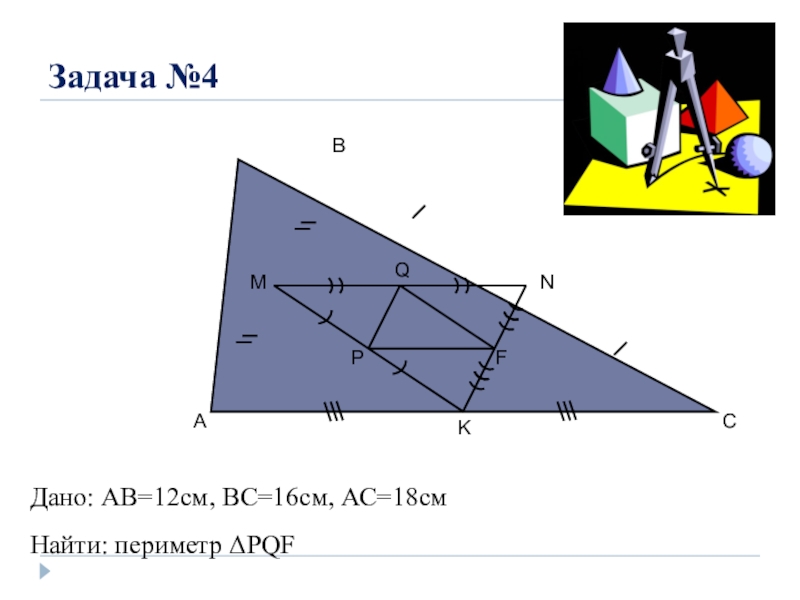
- 7. Задача №4ABCMNKPQFДано: AB=12cм, ВС=16см, АС=18смНайти: периметр ΔPQF
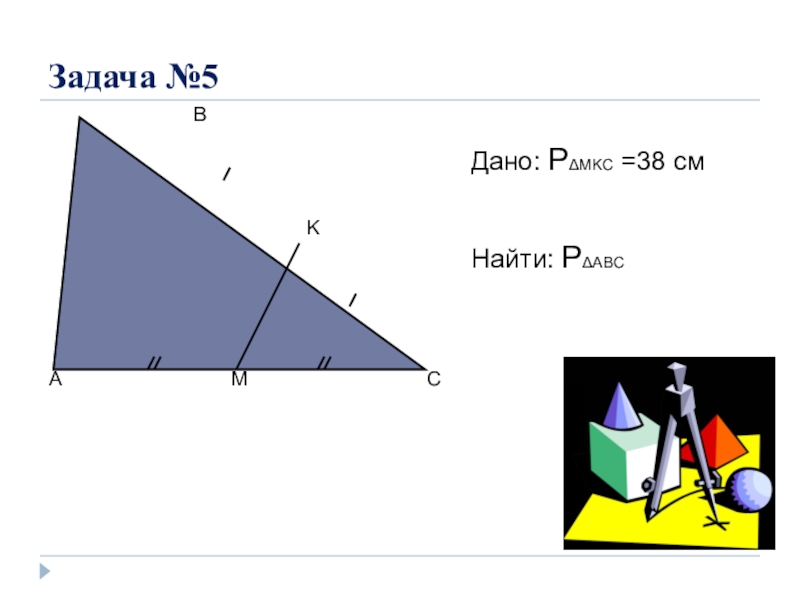
- 8. Задача №5ACBMKДано: PΔMKC =38 см Найти: PΔABC
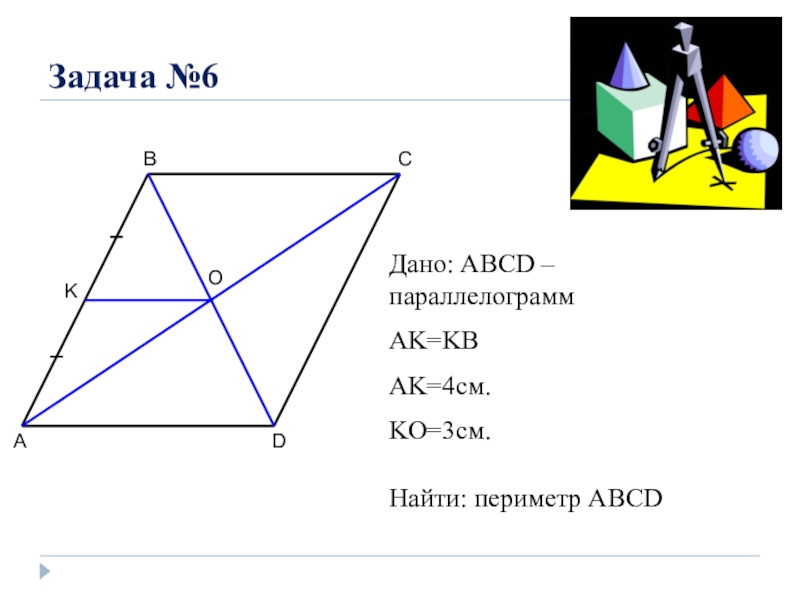
- 9. Задача №6ABCDOKДано: ABCD – параллелограммAK=KBAK=4см.KO=3см.Найти: периметр ABCD
- 10. Задача №7*ABCDMNKДано: ABCD – параллелограммAC=12см, BD=8смK, L,
- 11. Задача №8*ABCDMNKДано: ABCD – четырёхугольникK, L, M,
- 12. Вариньон Пьер(1654-1722)Теорема:Середины сторон произвольного четырёхугольника являются вершинами параллелограмма. Параллелограмм, образованный серединами сторон, иногда называется вариньоновским или вариньоновым.
- 13. Задача 9*ABCDEFO1O2Дано: ABCD, DCEF - четырёхугольникиAB=CD=EFAB ǁ
ОпределениеACBMNAM=MB, BN=NCMN – средняя линия треугольникаСредняя линия треугольника – это отрезок, соединяющий середины двух его сторон.
Слайд 2Определение
A
C
B
M
N
AM=MB, BN=NC
MN – средняя линия
треугольника
Средняя
линия треугольника – это отрезок, соединяющий середины двух его сторон.
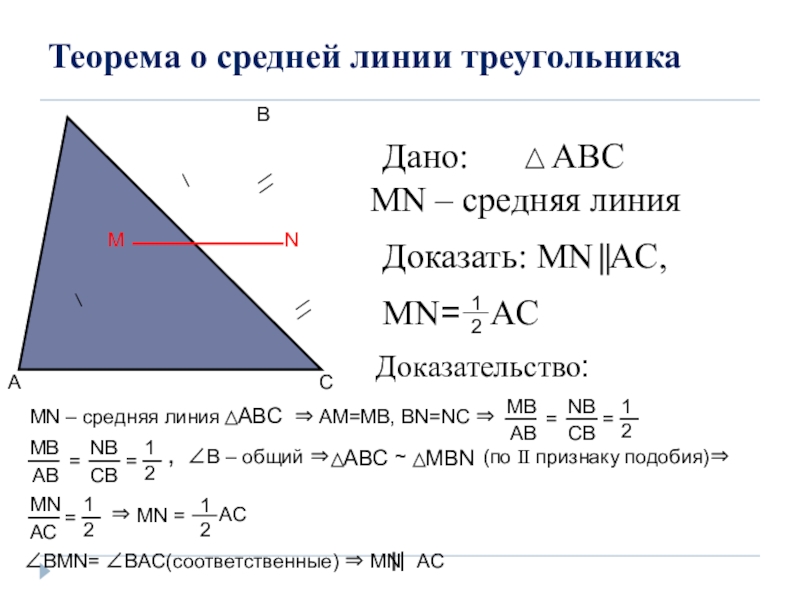
Слайд 3Теорема о средней линии треугольника
Дано:
MN – средняя линия
Доказать: MN AC,
MN=
1
2
AC
Доказательство:
МN – средняя линия
⇒ AM=MB, BN=NC ⇒
MB
AB
NB
CB
=
=
1
2
MB
AB
NB
CB
=
=
1
2
,
∠B – общий ⇒
~
(по II признаку подобия)⇒
MN
AC
=
1
2
∠BMN= ∠BAC(соответственные) ⇒ MN AC
⇒
MN =
1
2
AC
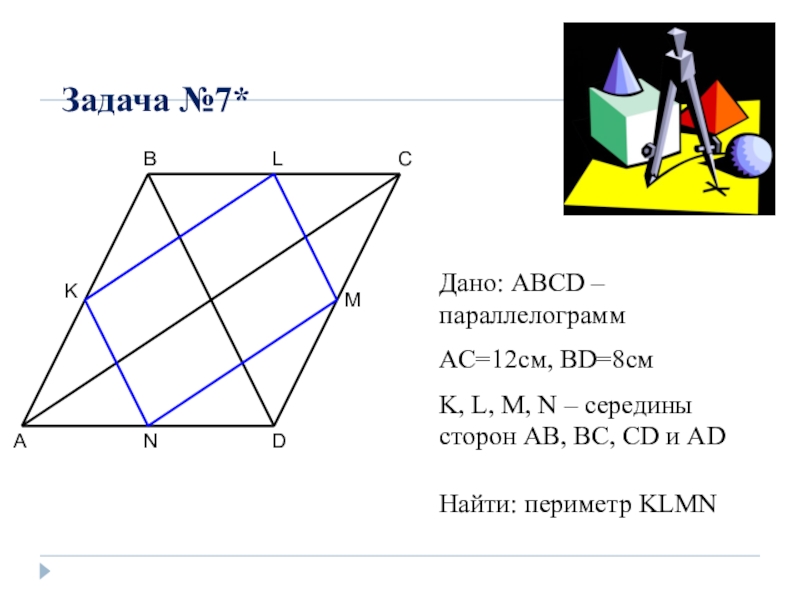
Слайд 10Задача №7*
A
B
C
D
M
N
K
Дано: ABCD – параллелограмм
AC=12см, BD=8см
K, L, M, N – середины
сторон AB, BC, CD и AD
Найти: периметр KLMN
Найти: периметр KLMN
L
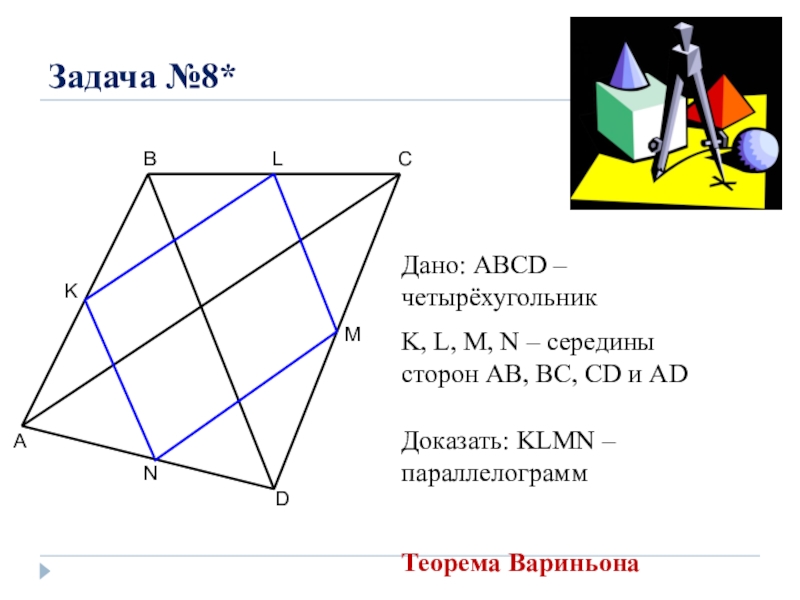
Слайд 11Задача №8*
A
B
C
D
M
N
K
Дано: ABCD – четырёхугольник
K, L, M, N – середины сторон
AB, BC, CD и AD
Доказать: KLMN – параллелограмм
Теорема Вариньона
Доказать: KLMN – параллелограмм
Теорема Вариньона
L
Слайд 12Вариньон Пьер
(1654-1722)
Теорема:
Середины сторон произвольного четырёхугольника
являются вершинами параллелограмма. Параллелограмм, образованный серединами сторон,
иногда называется вариньоновским или вариньоновым.
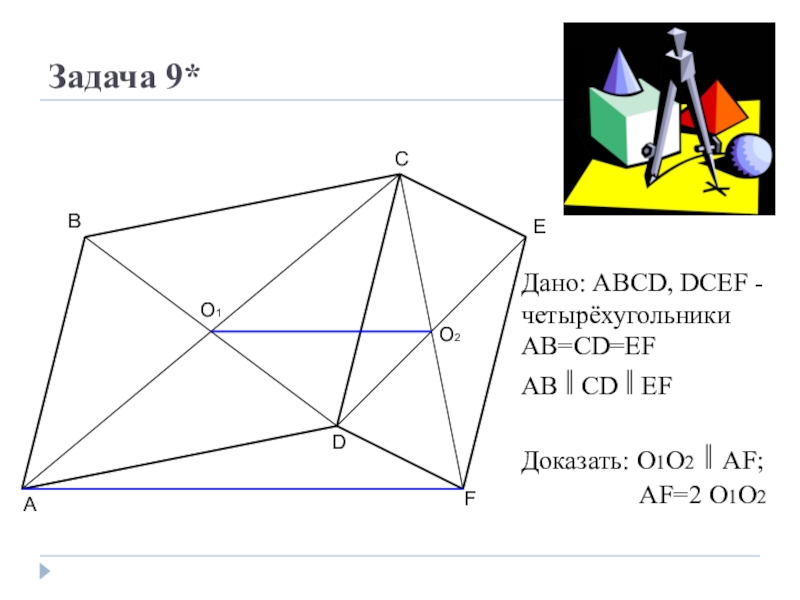
Слайд 13Задача 9*
A
B
C
D
E
F
O1
O2
Дано: ABCD, DCEF - четырёхугольники
AB=CD=EF
AB ǁ CD ǁ EF
Доказать: O1O2
ǁ AF;
AF=2 O1O2
AF=2 O1O2