- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Соотношения между сторонами прямоугольного треугольника
Содержание
- 1. Презентация по геометрии на тему Соотношения между сторонами прямоугольного треугольника
- 2. Введем обозначение A (маленькие
- 3. Основные определения: синус, косинус, тангенс и котангенс
- 4. Тангенсом острого угла прямоугольного треугольника называется отношение
- 5. Рассмотрим два прямоугольных треугольника с равным острым
- 6. Таким образом мы можем сделать вывод: если
- 7. Основное тригонометрическое тождество. Формула тангенса.Пользуясь определениями синуса,
- 8. Найдем значение синуса, косинуса и тангенса некоторых
- 9. Так как ∆ABC равнобедренный и прямоугольный, тогда
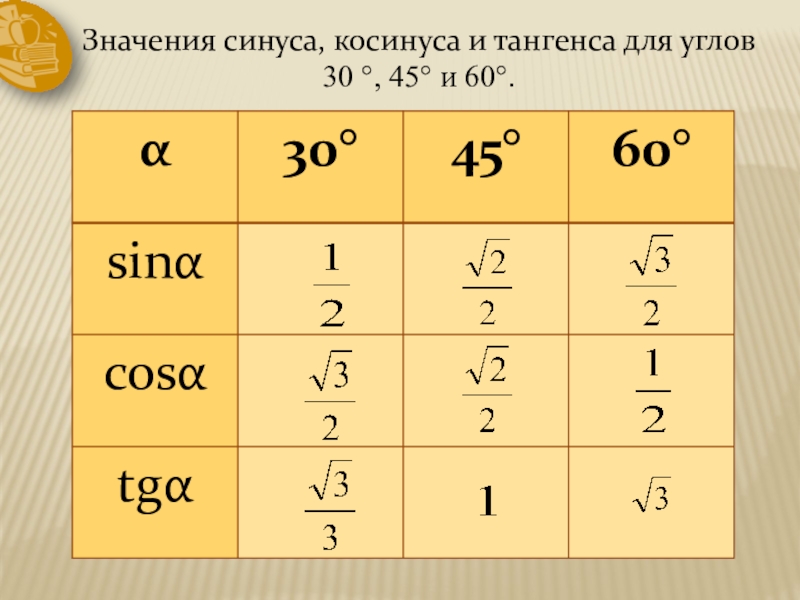
- 10. Значения синуса, косинуса и тангенса для углов 30 °, 45° и 60°.
Слайд 2Введем обозначение A (маленькие прописные буквы греческого алфавита
Актуализация
знаний
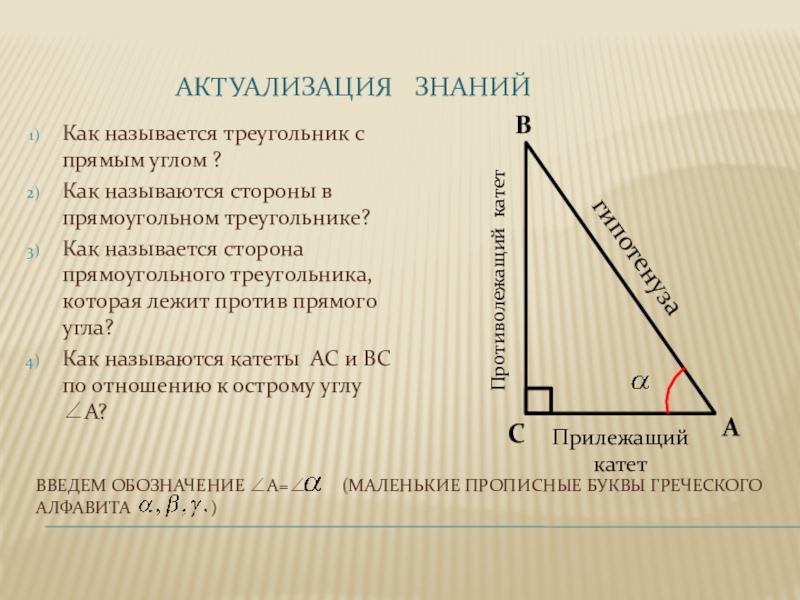
Как называется треугольник с прямым углом ?
Как называются стороны в прямоугольном треугольнике?
Как называется сторона прямоугольного треугольника, которая лежит против прямого угла?
Как называются катеты АС и ВС по отношению к острому углу А?
гипотенуза
Прилежащий катет
Противолежащий катет
Слайд 3Основные определения: синус, косинус, тангенс и котангенс острого угла в прямоугольном
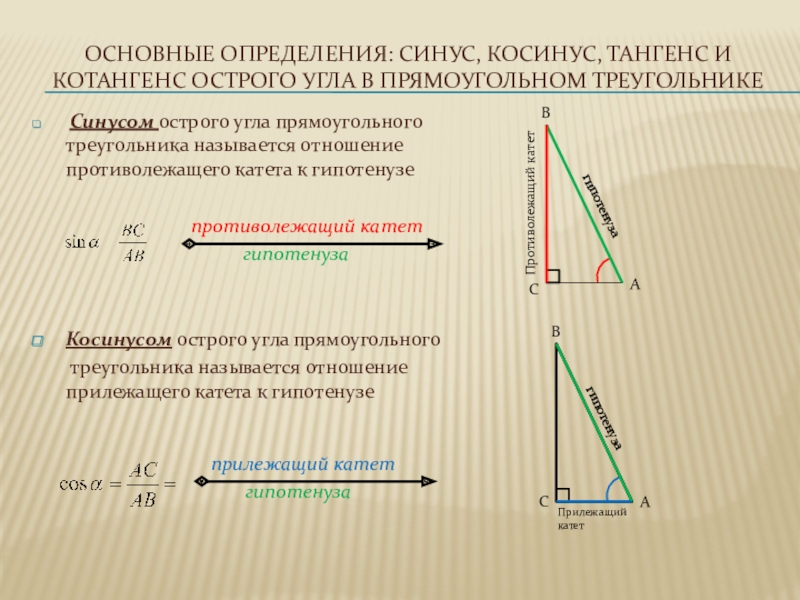
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе
противолежащий катет
гипотенуза
Косинусом острого угла прямоугольного
треугольника называется отношение прилежащего катета к гипотенузе
прилежащий катет
гипотенуза
Слайд 4
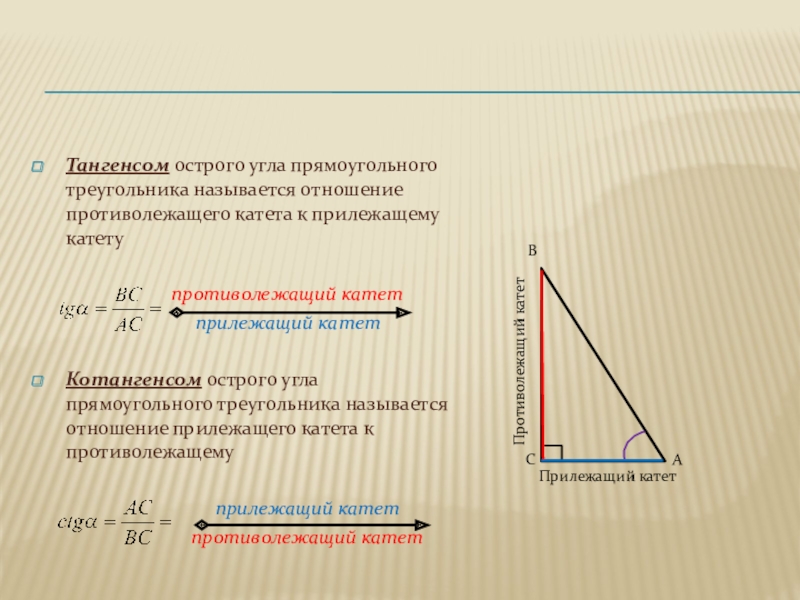
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему
противолежащий катет
прилежащий катет
Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему
прилежащий катет
противолежащий катет
Слайд 5Рассмотрим два прямоугольных треугольника с равным острым углом.
∆ABC~∆A1B1C1 по острому углу.
Найдем значения синуса, косинуса, тангенса и котангенс острого угла в данных треугольниках:
b
kc
ka
kb
a
c
Слайд 6Таким образом мы можем сделать вывод:
если острый угол одного прямоугольного
Т.е. значение синуса, косинуса, тангенса и котангенса не зависит от величины длин сторон при равных углах, а зависит только от размера угла.
Рассмотрим это на примере:
Задание . Дан треугольник ABC, угол А – прямой. Прямая DE параллельна AC. Найти синус, косинус и тангенс углов ACB, DEB, ABC и DBE.
A
В
С
D
E
Слайд 7Основное тригонометрическое тождество. Формула тангенса.
Пользуясь определениями синуса, косинуса и тангенса найдем
и
Итак
Таким образом мы получили, что
Найдем значение второго выражения:
По теореме Пифагора , тогда получаем, что
C
B
A
Слайд 8Найдем значение синуса, косинуса и тангенса некоторых острых углов в прямоугольном
Рассмотрим равносторонний треугольник ∆ABC со стороной 8:
Каждый угол равен 60°. Высота, проведенная из вершины В, является медианой стороны АС и биссектрисой угла AВC. Таким образом, мы получили прямоугольный треугольник ABH: BAH=60°, AHB=90°, ABH=30º
гипотенуза АВ=8, катет AH=4.
По теореме Пифагора найдем катет BH:
A
B
H
C
8
4
Найдем значения синуса, косинуса и тангенса углов ABH=30º и BAH=60°:
60º
30º
Слайд 9Так как ∆ABC равнобедренный и прямоугольный, тогда катеты равна, т.е. AC=BC,
Пусть сторона AC=BC=5, тогда по теореме Пифагора найдем гипотенузу:
Найдем синус, косинус и тангенс угла BAC:
Для угла ABC значения синуса, косинуса и тангенса будут такие же.
Таким образом, мы вычислили значения синуса, косинуса и тангенса для углов 30º, 45º и 60º. Занесем полученные результаты в таблицу и выучим!
Теперь рассмотрим прямоугольный равнобедренный треугольник и найдем значения
синуса, косинуса и тангенса его острых углов.