некоторые их свойства»
(7 класс)
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Прямоугольные треугольники и некоторые их свойства
Содержание
- 1. Презентация по геометрии на тему Прямоугольные треугольники и некоторые их свойства
- 2. Прямоугольные треугольники некоторые их свойства и
- 3. Цели: 1. Рассмотреть свойства прямоугольных треугольников; 2. Уметь решать задачи
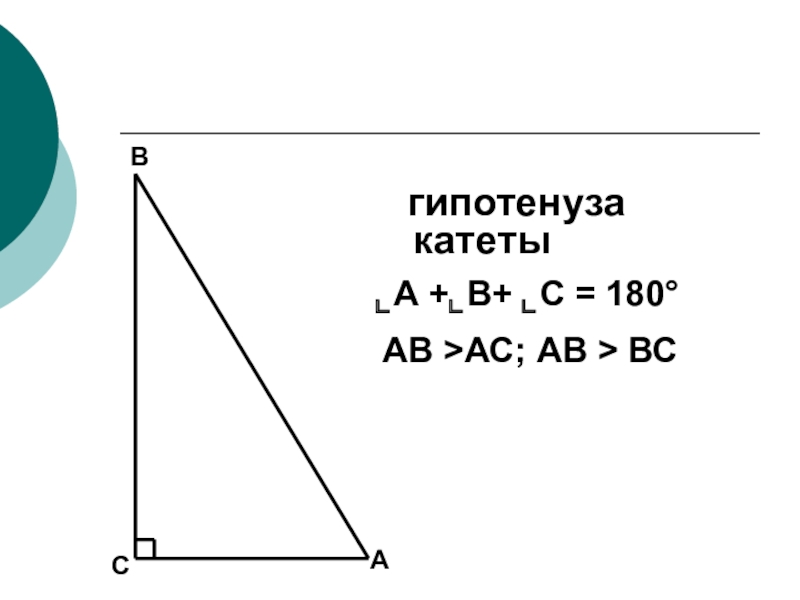
- 4. АВСгипотенузакатетыАВ >АС; АВ > ВС ⌞А +⌞В+ ⌞С = 180°
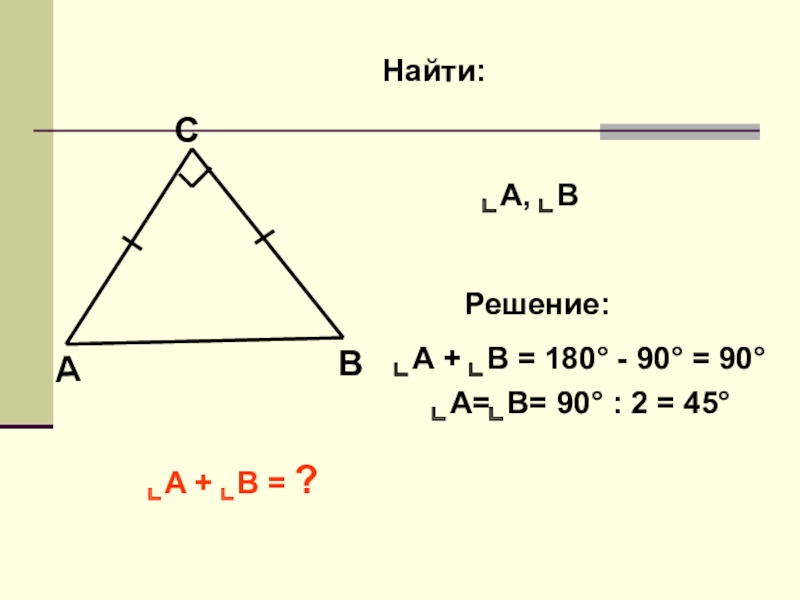
- 5. АВСНайти:⌞А, ⌞ВРешение:⌞А=⌞В= 90° : 2 = 45°⌞А
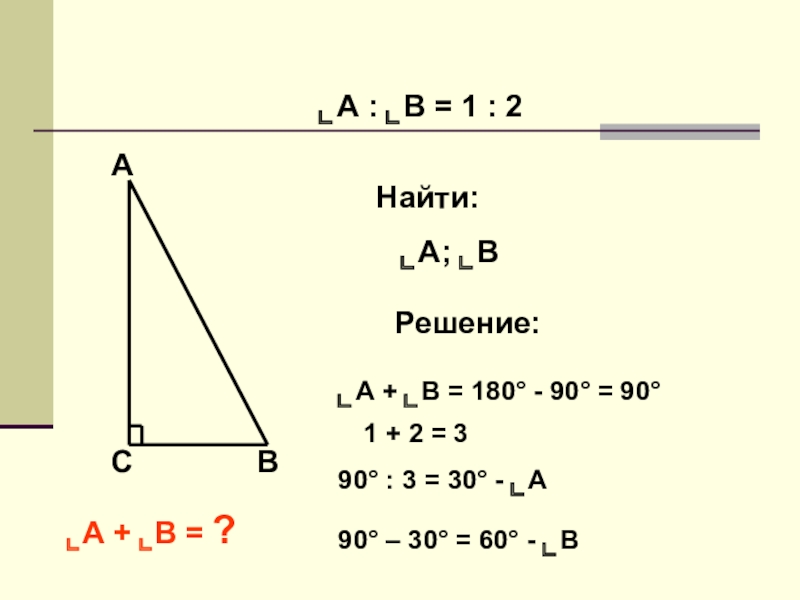
- 6. СВА⌞А : ⌞В = 1 : 2Найти:⌞А;
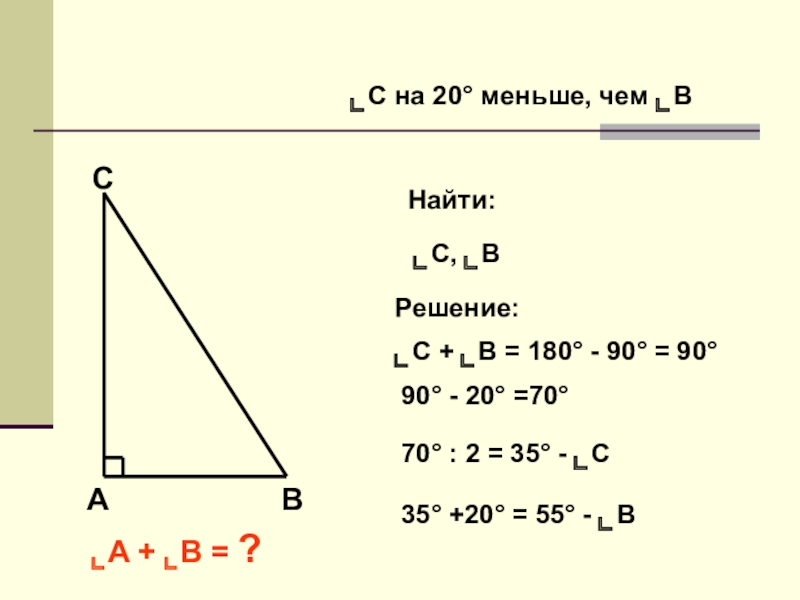
- 7. АВС⌞С на 20° меньше, чем ⌞ВНайти:⌞С, ⌞ВРешение:⌞С
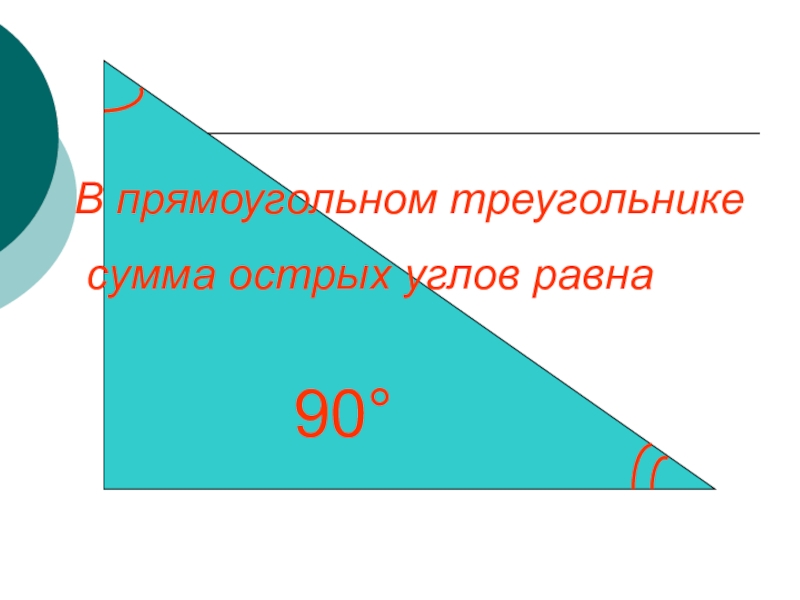
- 8. В прямоугольном треугольнике сумма острых углов равна
- 9. АСВD30°Доказать: АD = ½ АВРешение:∆ АВС –
- 10. АВСDАD = ½ АВНайти:углы ∆АВDРешение:∆АВС – равнобедренныйВD-
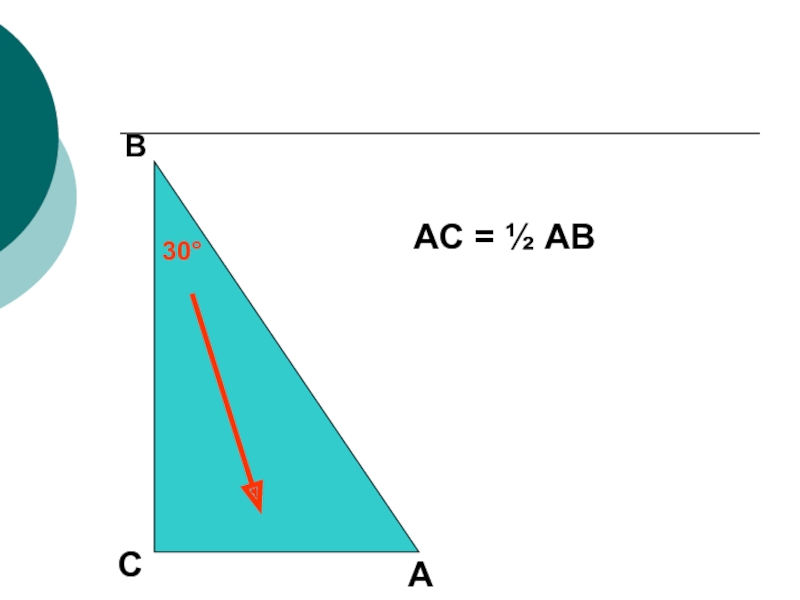
- 11. АВСАС = ½ АВ30°
- 12. Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
- 13. АВСДано: ∆АВС, ⌞А = 90°, ⌞В =
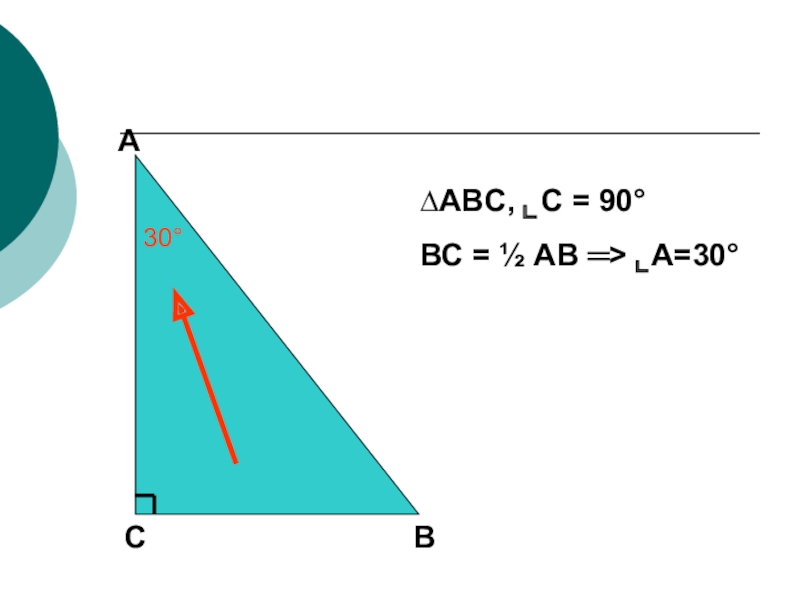
- 14. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°
- 15. АВС∆ABC, ⌞C = 90°ВС = ½ АВ ═> ⌞A=30°30°
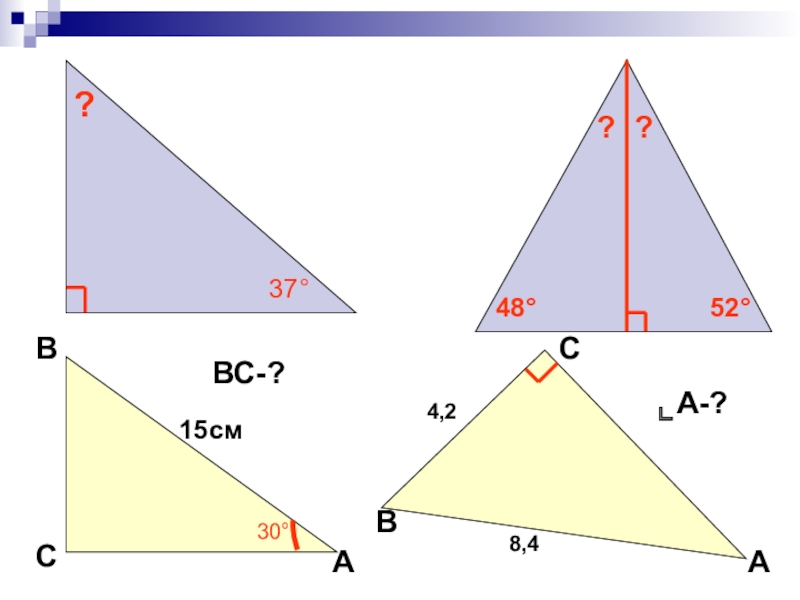
- 16. 37°48°52°СВА30°15смВАС4,28,4ВС-?⌞А-????
Прямоугольные треугольники некоторые их свойства и
Слайд 6С
В
А
⌞А : ⌞В = 1 : 2
Найти:
⌞А; ⌞В
Решение:
⌞А + ⌞В =
180° - 90° = 90°
1 + 2 = 3
90° : 3 = 30° - ⌞А
90° – 30° = 60° - ⌞В
⌞А + ⌞В = ?
Слайд 7А
В
С
⌞С на 20° меньше, чем ⌞В
Найти:
⌞С, ⌞В
Решение:
⌞С + ⌞В = 180°
- 90° = 90°
90° - 20° =70°
70° : 2 = 35° - ⌞С
35° +20° = 55° - ⌞В
⌞А + ⌞В = ?
Слайд 9
А
С
В
D
30°
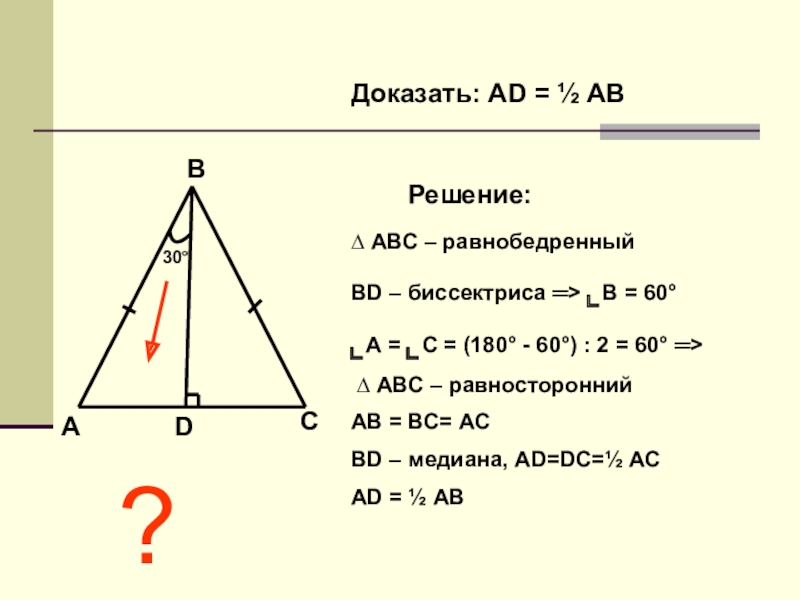
Доказать: АD = ½ АВ
Решение:
∆ АВС – равнобедренный
ВD – биссектриса ═>
⌞В = 60°
⌞А = ⌞С = (180° - 60°) : 2 = 60° ═>
∆ АВС – равносторонний
АВ = ВС= АС
ВD – медиана, АD=DС=½ АС
АD = ½ АВ
⌞А = ⌞С = (180° - 60°) : 2 = 60° ═>
∆ АВС – равносторонний
АВ = ВС= АС
ВD – медиана, АD=DС=½ АС
АD = ½ АВ
?
Слайд 10А
В
С
D
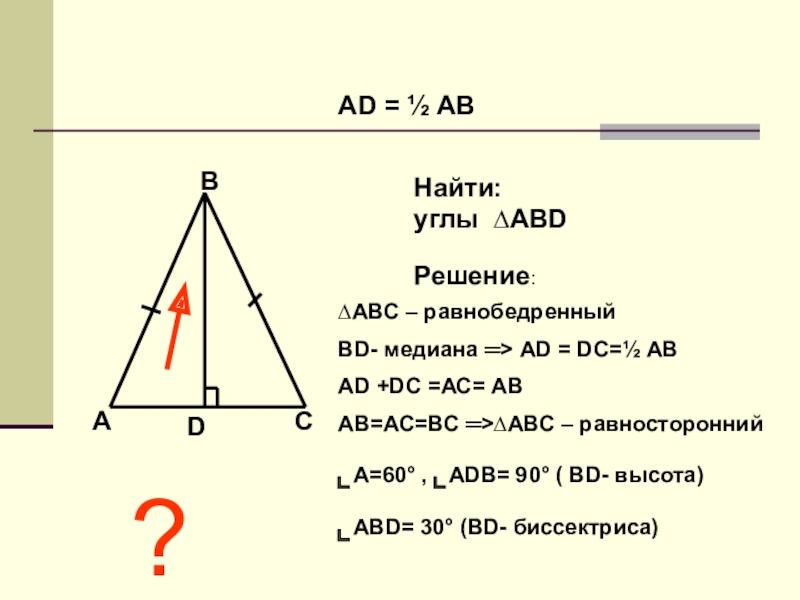
АD = ½ АВ
Найти:
углы ∆АВD
Решение:
∆АВС – равнобедренный
ВD- медиана ═> АD =
DС=½ АВ
АD +DС =АС= АВ
АВ=АС=ВС ═>∆АВС – равносторонний
⌞А=60° , ⌞АDВ= 90° ( ВD- высота)
⌞АВD= 30° (ВD- биссектриса)
АD +DС =АС= АВ
АВ=АС=ВС ═>∆АВС – равносторонний
⌞А=60° , ⌞АDВ= 90° ( ВD- высота)
⌞АВD= 30° (ВD- биссектриса)
?
Слайд 13А
В
С
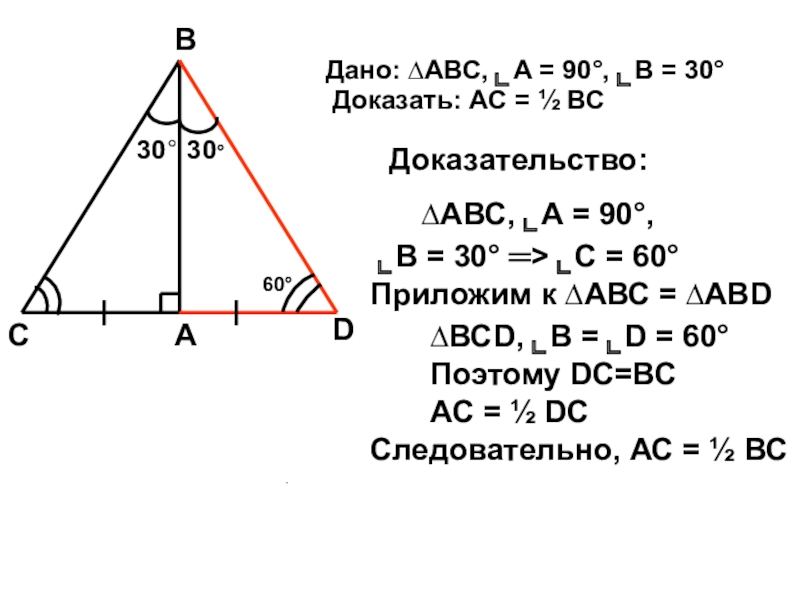
Дано: ∆АВС, ⌞А = 90°, ⌞В = 30°
Доказать: АС = ½
ВС
D
30°
Доказательство:
∆АВС, ⌞А = 90°,
⌞В = 30° ═> ⌞С = 60° Приложим к ∆АВС = ∆АВD
∆ВСD, ⌞В = ⌞D = 60°
Поэтому DС=ВС
АС = ½ DС
Следовательно, АС = ½ ВС
60°
30°
Слайд 14Если катет прямоугольного треугольника
равен половине гипотенузы, то угол,
лежащий против
этого катета, равен 30°
